Harris C.M., Piersol A.G. Harris Shock and vibration handbook

Подождите немного. Документ загружается.

tion of the supported equipment above

and below the static equilibrium posi-

tion, as indicated in Fig. 30.32. Thus, the

natural frequency is determined solely

by the stiffness characteristics in the

region of the isolator deflection.

NATURAL FREQUENCY

In determining the natural frequency of

a nonlinear isolator, it is important to

note whether or not all the load results

from the dead weight of a massive body.

The force F on the isolator may be

greater than the weight W because of a

belt pull or sustained acceleration of a

missile. Then the load on the isolator is

F = n

W (30.57)

where n

is some multiple of the acceleration of gravity. For example, n

may indi-

cate the absolute value of the sustained acceleration of a missile measured in “num-

ber of g’s.”

Characteristic of Tangent Isolator. It is convenient to define the force-

deflection characteristics of a nonlinear isolator having increasing stiffness (harden-

ing characteristic) by a tangent function:

F = tan



(30.58)

where F is the total force applied to the isolator, k

is the stiffness of the isolator at

zero deflection, δ is the deflection of the isolator, and h

is the characteristic height

of the isolator. The force-deflection characteristic defined by Eq. (30.58) is shown

graphically in Fig. 30.33A. The characteristic height h

represents a height or thick-

ness characteristic of the isolator which may be adjusted empirically to obtain opti-

mum agreement, over the deflection range of interest, between Eq. (30.58) and the

actual force-deflection curve for the isolator.

The stiffness of the tangent isolator is obtained by differentiation of Eq. (30.58)

with respect to δ:

k ==k

sec



= k



1 +





(30.59)

The stiffness-deflection relation defined by Eq. (30.59) is shown graphically in Fig.

30.33B.

Replacing the load F by n

W in Eq. (30.59) and substituting the resulting stiffness

relation into Eq. (30.56):





= 3.13



2.46n



(30.60)



Fπ



πδ



dδ

πδ



THEORY OF VIBRATION ISOLATION 30.39

FIGURE 30.32 Typical force-deflection char-

acteristic of a tangent hardening isolator.

8434_Harris_30_b.qxd 09/20/2001 11:41 AM Page 30.39

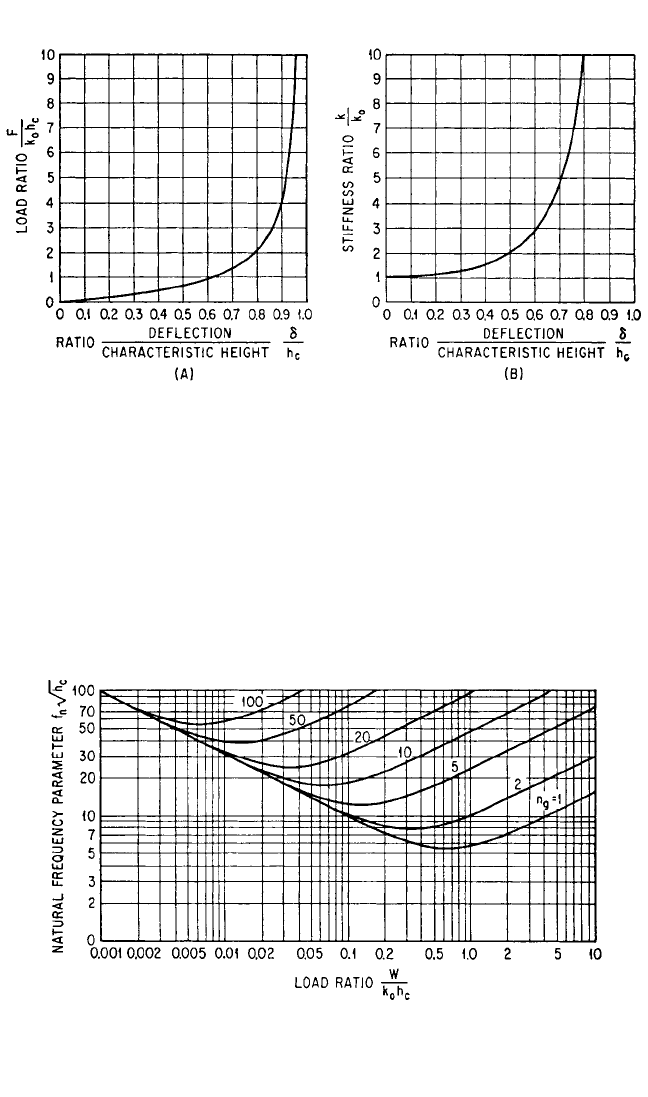
The relation defined by Eq. (30.60) is shown graphically in Fig. 30.34. The ordinate is

the natural frequency f

(Hz) times the square root of the characteristic height of the

isolator (in.). The theoretical and experimental force-deflection curves for the isola-

tor are matched to establish the numerical value of the characteristic height. For a

given value of the acceleration parameter n

, the natural frequency of the isolation

system is determined by h

and W/k

The deflection of the isolator under a sustained acceleration loading is obtained

by substituting Eq. (30.57) into the general force-deflection expression, Eq. (30.58),

and solving for the dimensionless ratio δ/h

30.40 CHAPTER THIRTY

FIGURE 30.33 Elastic properties of a tangent isolator in terms of its characteristic height h

and

stiffness k

at zero deflection: (A) dimensionless force-deflection curve; (B) dimensionless stiffness-

deflection curve.

FIGURE 30.34 Natural frequency f

of a tangent isolator system when a portion of

the total load applied to the isolator is nonmassive. The weight carried by the isolator is

W and the sustained acceleration parameter is n

, a multiple of the gravitational accel-

eration. The characteristic height is h

and the stiffness at zero deflection is k

8434_Harris_30_b.qxd 09/20/2001 11:41 AM Page 30.40

= tan

−1



⋅



= tan

−1



15.37



(30.61)

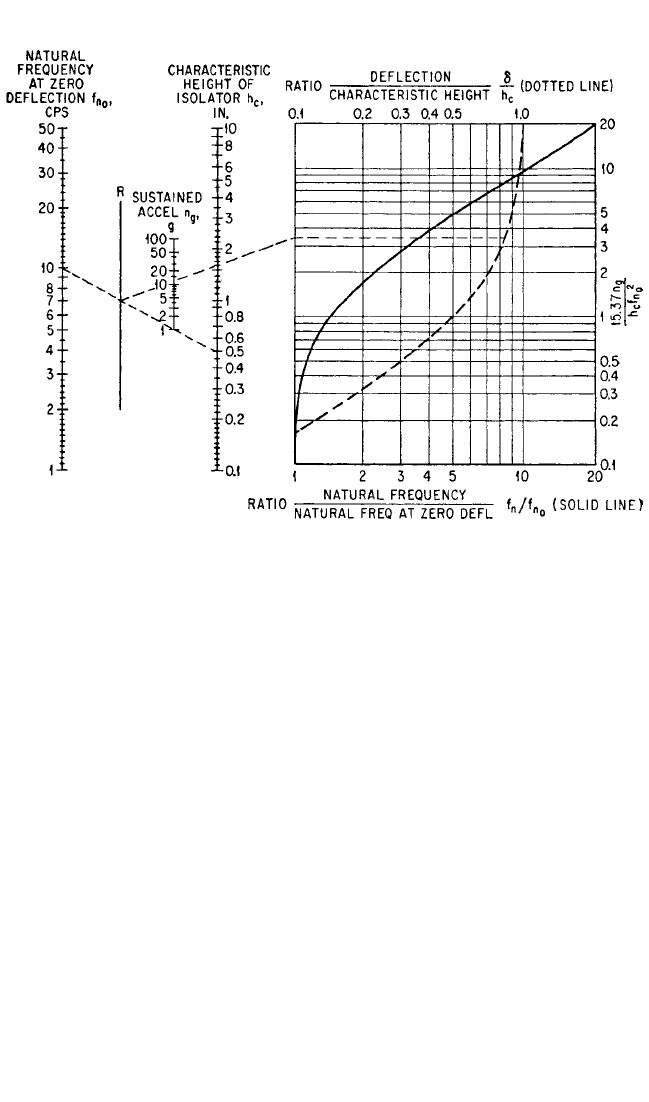
A reference natural frequency f

is the natural frequency that occurs when the iso-

lator is not deflected by the dead-weight load; i.e., n

= 0. The nomograph of Fig.

30.35 gives the deflection ratio δ/h

and the frequency ratio f

The value of the

parameter 15.37(n

) is transferred by a horizontal projection to the coordi-

nate system for the curves.Values for the natural frequency ratio f

are read from

the lower abscissa scale and values for the deflection ratio δ/h

are read from the

upper abscissa scale.

Example 30.3. A rubber isolator having a characteristic height h

= 0.5 in.

(determined experimentally for the particular isolator design) has a natural fre-

quency f

= 10 Hz for small deflections and a fraction of critical damping ζ=0.2.The

equipment supported by the isolator is subjected to a sustained acceleration of 11g.

It is desired to determine the absolute transmissibility of the isolation system when

the forcing frequency is 100 Hz, and to determine the deflection of the isolator under

the sustained acceleration.

Referring to the nomograph of Fig. 30.35, a straight line is drawn from a value of

10 on the f

scale to 0.5 on the h

scale. A second straight line is drawn from the

intersection of the first line with the R scale through the value n

= 11. The second

line intersects the left side of the coordinate system and is extended horizontally so

that it intersects the solid and dotted curves.The intersection points indicate that the



πn



THEORY OF VIBRATION ISOLATION 30.41

FIGURE 30.35 Nomograph and curve for determining the natural frequency and deflection of an

isolation system incorporating a tangent isolator when a portion of the total load applied to the iso-

lator is nonmassive.

8434_Harris_30_b.qxd 09/20/2001 11:41 AM Page 30.41

natural frequency ratio f

= 3.5 and the deflection ratio δ/h

= 0.81.The deflection

of the isolator at equilibrium as a result of the sustained acceleration is 0.81h

= 0.405

in. The undamped natural frequency for the sustained acceleration of 11g is f

= 3.5

× 10 = 35 Hz. The natural frequency also can be obtained from Fig. 30.34 by noting

that W/k

= (g/h

)/(2πf

)

= 0.196 [see Eq. (30.60) when n

= 0].Then for n

= 11, f

= 24.5/





= 35 Hz.

From Fig. 30.2 the transmissibility for ζ=0.2, f/f

= 100/35 = 2.88 is 0.22. In the

absence of the sustained acceleration, the corresponding transmissibility would be

0.042 as obtained from Fig. 30.2 at f/f

= 100/10 = 10. Thus, the transmissibility at 100

Hz under a sustained acceleration of 11g is 5 times as great as that which would exist

for a dead-weight loading of the isolator.

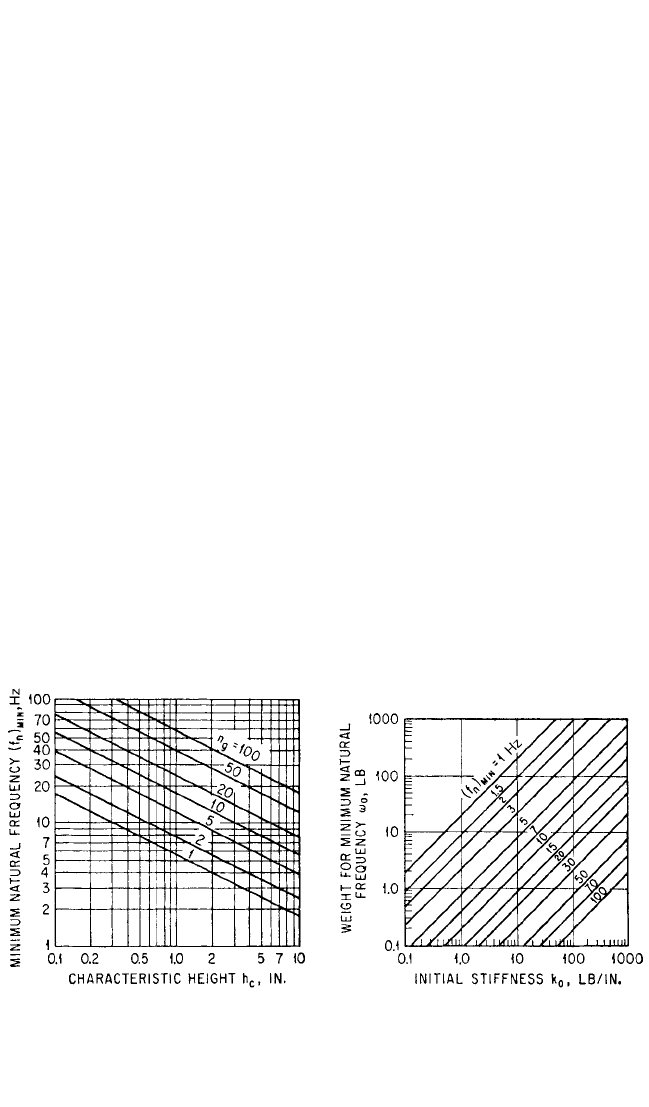
Minimum Natural Frequency. The weight W

for which a given tangent isola-

tor has a minimum natural frequency is

== [ f

= minimum] (30.62)

where the minimum natural frequency (f

)

min

is defined by

)

min





(30.63)

The minimum natural frequency is shown graphically in Fig. 30.36 as a function of

the characteristic height h

and the sustained acceleration parameter n

. The weight

required to produce the minimum natural frequency (f

)

min

is shown graphically

in Fig. 30.37 as a function of the initial stiffness k

and the minimum natural fre-

quency (f

)

min

. When the isolator is loaded to produce the minimum natural fre-

quency, the isolator deflection is one-half the characteristic height (δ=h

/2) and the

stiffness under load is twice the initial stiffness (k = 2k



πh





2π

( f

)

min



πn

30.42 CHAPTER THIRTY

FIGURE 30.36 Minimum natural frequency

n(min)

of a tangent isolator system as a function of

(1) the characteristic height h

of the isolator and

(2) the sustained acceleration n

expressed as a

multiple of the gravitational acceleration.

FIGURE 30.37 Weight loading W

required to

cause a tangent isolator to have a minimum nat-

ural frequency f

n(min)

, as a function of the stiffness

at zero deflection.

8434_Harris_30_b.qxd 09/20/2001 11:41 AM Page 30.42

ISOLATION OF RANDOM VIBRATION

In random vibration, all frequencies exist concurrently, and the amplitude and phase

relations are distributed in a random manner. A trace of random vibration is illus-

trated in Fig. 11.1A. The equipment-isolator assembly responds to the random vibra-

tion with the substantially single-frequency pattern shown in Fig. 11.1B. This response

is similar to a sinusoidal motion with a continuously and irregularly varying envelope;

it is described as narrow-band random vibration or a random sine wave.

The characteristics of random vibration are defined by a frequency spectrum of

power spectral density (see Chaps. 11 and 22). This is a generic term used to desig-

nate the mean-square value of some magnitude parameter passed by a filter, divided

by the bandwidth of the filter, and plotted as a spectrum of frequency. The magni-

tude is commonly measured as acceleration in units of g; then the particular expres-

sion to use in place of power spectral density is mean-square acceleration density,

commonly expressed in units of g

/Hz. When the spectrum of mean-square acceler-

ation density is substantially flat in the frequency region extending on either side of

the natural frequency of the isolator, the response of the isolator may be determined

in terms of (1) the mean-square acceleration density of the isolated equipment and

(2) the deflection of the isolator at successive cycles of vibration.

The mean-square acceleration densities of the foundation and the isolated equip-

ment are related by the absolute transmissibility that applies to sinusoidal vibration:

( f ) = W

( f )T

(30.64)

where W

( f ) and W

( f ) are the mean-square acceleration densities of the equip-

ment and the foundation, respectively, in units of g

/Hz and T

is the absolute trans-

missibility for the vibration-isolation system.

REFERENCES

1. Crede, C. E.: “Vibration and Shock Isolation,” John Wiley & Sons, Inc., New York, 1951.

2. Den Hartog, J. P.: Trans. ASME, APM-53-9, 1932.

3. Jacobsen, L. S.: Trans. ASME, APM-52-15, 1931.

4. Crede, C. E., and J. P. Walsh: J.Appl. Mechanics, 14:1A-7 (1947).

5. Lewis, R. C., and K. Unholtz: Trans.ASME, 69:8 (1947).

6. Crede, C. E.: J.Appl. Mechanics, 25:541 (1958).

7. Timoshenko, S., and G. H. MacCullough:“Elements of Strength of Materials,” 3d ed., p. 64,

D. Van Nostrand Company, Inc., Princeton, N.J., 1949.

8. Mindlin, R. D.: Bell System Tech. J., 24(3–4):353 (1945).

9. Crede, C. E.: Trans. ASME, 76(1):117 (1954).

THEORY OF VIBRATION ISOLATION 30.43

8434_Harris_30_b.qxd 09/20/2001 11:41 AM Page 30.43

CHAPTER 31

THEORY OF

SHOCK ISOLATION

R. E. Newton

INTRODUCTION

This chapter presents an analytical treatment of the isolation of shock. Two classes

of shock are considered: (1) shock characterized by motion of a support or founda-

tion where a shock isolator reduces the severity of the shock experienced by equip-

ment mounted on the support and (2) shock characterized by forces applied to or

originating within a machine where a shock isolator reduces the severity of shock

experienced by the support. In the simplified concept of shock isolation, the equip-

ment and support are considered rigid bodies, and the effectiveness of the isolator is

measured by the forces transmitted through the isolator (resulting in acceleration of

equipment if assumed rigid) and by the deflection of the isolator. Linear isolators,

both damped and undamped, together with isolators having special types of nonlin-

ear elasticity are considered.When the equipment or floor is not rigid, the deflection

of nonrigid members is significant in evaluating the effectiveness of isolators.Analy-

ses of shock isolation are included which consider the response of nonrigid compo-

nents of the equipment and floor.

IDEALIZATION OF THE SYSTEM

In the application of shock isolators to actual equipments, the locations of the isola-

tors are determined largely by practical mechanical considerations. In general, this

results in types of nonsymmetry and coupled modes not well adapted to analysis by

simple means. It is convenient in the design of shock isolators to idealize the system

to a hypothetical one having symmetry and uncoupled modes of motion.

UNCOUPLED MOTIONS

The first step in idealizing the physical system is to separate the various translational

and rotational modes, i.e., to uncouple the system. Consider the system of Fig. 31.1

31.1

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.1

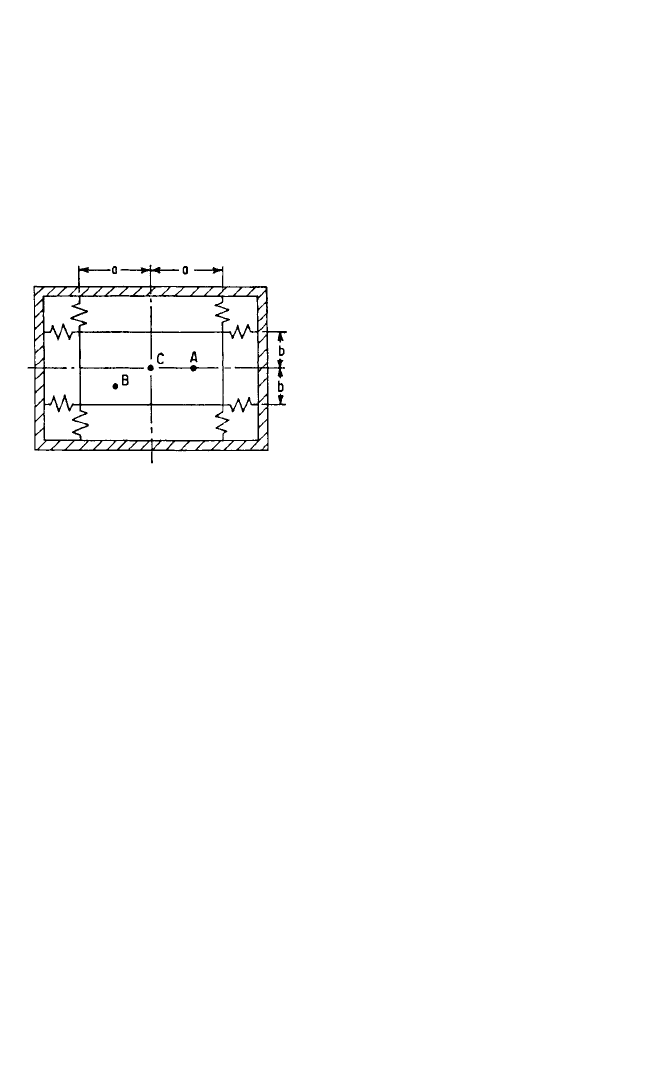
consisting of a homogeneous block attached at the corners, by eight identical springs,

to a movable rigid frame. The block and frame are constrained to move in the plane

of the paper.With the system at rest, the frame is given a sudden vertical translation.

Because of the symmetry of both mass and stiffness relative to a vertical plane per-

pendicular to the paper, the response motion of the block is pure vertical translation.

Similarly, a sudden horizontal translation of the frame excites pure horizontal trans-

lation of the block.A sudden rotation about an axis through the geometric center of

the block produces pure rotation of the block about this axis. This set of response

behaviors is characteristic of an uncoupled system.

If the block of Fig. 31.1 is not homoge-

neous, the mass center (or center-of-

gravity) may be at A or B instead of C.

Consider the response to a sudden verti-

cal translation of the frame if the mass

center is at A. If the response were pure

vertical translation of the block, the

dynamic forces induced in the vertical

springs would have a resultant acting ver-

tically through C. However, the “inertia

force” of the block must act through the

mass center at A. Thus, the response can-

not be pure vertical translation, but must

also include rotation. Then the motions

of vertical translation and rotation are

said to be coupled. A sudden horizontal

translation of the frame would still excite

only a horizontal translation of the block because A is symmetrical with respect to the

horizontal springs; thus this horizontal motion remains uncoupled. If the mass center

were at B, i.e., in neither the vertical nor the horizontal plane of symmetry, then a sud-

den vertical translation of the frame would excite both vertical and horizontal transla-

tions of the block, together with rotation. In this case, all three motions are said to be

coupled.

It is not essential that a system have any kind of geometric symmetry in order

that its motions be uncoupled, but rather that the resultant of the spring forces be

either a force directed through the center-of-gravity of the block or a couple. If the

motions are completely uncoupled, there are three mutually orthogonal directions

such that translational motion of the base in any one of these directions excites only

a translation of the body in the same direction. Similarly there are three orthogonal

axes, concurrent at the mass center, having the property that a pure rotation of the

base about any one of these axes will excite a pure rotation of the body about the

same axis. The idealized systems considered in this chapter are assumed to have

uncoupled rigid body motions.

ANALOGY BETWEEN TRANSLATION AND ROTATION

If the motions in translational and rotational modes are uncoupled, motion in the

rotational mode may be inferred by analogy from motion in the translational mode,

and vice versa. Consider the system of Fig. 31.1.Assume that the mass center is at C

and the forces in the four vertical springs have a negligible horizontal component at

all times. For horizontal motion the differential equation of motion is

31.2 CHAPTER THIRTY-ONE

FIGURE 31.1 Schematic diagram of three

degree-of-freedom mounting.

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.2

δ+4kδ=−mü (31.1)

where δ= horizontal displacement of mass center of block relative to center-of-

frame, in.

m = mass of block, lb-sec

/in.

k = spring stiffness for each spring, lb/in.

u = absolute horizontal displacement of center-of-frame, in. In the

equilibrium position the point C lies at the frame center.

Equation (31.1) may be written

δ+ω

δ=−ü (31.2)

where ω





, rad/sec, is the angular natural frequency in horizontal vibration.

For rotation of the block the corresponding equation of motion is

I ¨γ

+ 4k(a

+ b

)γ

=−I

G (31.3)

where I = mass moment of inertia of block about axis through C, perpendicular

to plane of paper, lb-in.-sec

a, b = distances of spring center lines from mass center (see Fig. 31.1), in.

= rotation of block relative to frame in plane of paper, rad

G = absolute rotation of frame in plane of figure, rad

Equation (31.3) may be written

¨γ

+ω

=−

G (31.4)

where ω





)



is the angular natural frequency in rotation.

Equations (31.2) and (31.4) are analogous; γ

corresponds to δ, G corresponds to

u, and ω

corresponds to ω

. Because of this analogy, only the horizontal motion

described by Eq. (31.2) is considered in subsequent sections; corresponding results

for rotational motion may be determined by analogy.

CLASSIFICATION OF SHOCK ISOLATION

PROBLEMS

It is convenient to divide shock isolation problems into two major classifications

according to the physical conditions:

Class I. Mitigation of effects of foundation motion

Class II. Mitigation of effects of force generated by equipment

Isolators in the first class include such items as the draft gear on a railroad car, the

shock strut of an aircraft landing gear, the mounts on airborne electronic equipment,

and the corrugated paper used to package light bulbs. The second class includes the

recoil cylinders on gun mounts and the isolators on drop hammers, looms, and recip-

rocating presses.The objectives in the two classes of problems are allied, but distinct.

In Class I the objective is to limit the shock-induced stresses in critical components

of the protected equipment. In Class II the purpose is to limit the forces transmitted

to the support for the equipment in which the shock originates.

THEORY OF SHOCK ISOLATION 31.3

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.3

IDEALIZED SYSTEMS—CLASS I

The simplest approach to problems of Class I is through a study of single degree-of-

freedom systems (see Chap. 2). Consider the system of Fig. 31.2A. The basic ele-

ments are a mass and a spring-dashpot unit attached to the mass at one end. The

block may be taken to represent the equipment (assumed to be a rigid body), and

the spring-dashpot unit to represent the shock isolator.The displacement of the sup-

port is u. The equation of motion is

δ+F(

δ,δ) =−mü (31.5)

where m = mass of block, lb-sec

/in.

δ= deflection of spring (δ=x − u; see Fig. 31.2), in.

δ,δ) = force exerted on mass by spring-dashpot unit (positive when ten-

sile), lb

u = absolute displacement of left-hand end of spring-dashpot unit, in.

In the typical shock isolation problem, the system of Fig. 31.2A is initially at rest (

u =

δ=0) in an equilibrium position (u =δ=0).An external shock causes the support to

move.The corresponding movement of the left end of the shock isolator is described

in terms of the support acceleration ü. Then Eq. (31.5) may be solved for the result-

ing extreme values of δ and F(

δ,δ), and these values may be compared with the per-

missible deflection and force transmission limits of the shock isolator. It also is

necessary to determine whether the internal stresses developed in the equipment

are excessive. If the equipment is sufficiently rigid that all parts have substan-

tially equal accelerations, then the internal stresses are proportional to

x where

−m

x = F(

δ,δ).

A critical component of the equipment may be sufficiently flexible to have a sub-

stantially different acceleration than that determined by assuming the equipment

rigid. If the total mass of such components is small in comparison with the equip-

ment mass, the above analysis may be extended to cover this case. Equation (31.5) is

first solved to determine not merely the extreme value of F(

δ,δ) but its time-history.

Then the acceleration

x may be determined from the relation

x =−F(

δ,δ)/m. Now

consider the system shown in Fig. 31.2B having a component of mass m

and stiffness-

damping characteristics F

(

,δ

). The force F

(

,δ

) transmitted to the mass m

and

the resulting acceleration

=−F

(

,δ

)/m

may be found by solving an equation

that is analogous to Eq. (31.5) where

x is substituted for ü,

for

δ, and F

(

,δ

) for

δ,δ).

31.4 CHAPTER THIRTY-ONE

FIGURE 31.2 Idealized systems showing use of isolator with transmitted force F(

δ,δ) to protect

equipment of mass m from effects of support motion u. In (A) the equipment is rigid and in (B) there

is a flexible component having stiffness-damping characteristics F

(

, δ

) and mass m

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.4

IDEALIZED SYSTEMS—CLASS II

Consider the system of Fig. 31.3A to represent the equipment (mass m) attached to its

support by the shock isolator (spring-dashpot unit).The left end of the spring-dashpot

unit is fixed to the supporting structure and there is a force F applied externally to the

mass.The force F may be a real external force or it may be an “inertia force” generated

by moving parts of the equipment. The equation of motion may be written as

δ+F(

δ,δ) = F (31.6)

where F is the external force applied to the mass in pounds and the relative dis-

placement δ of the ends of the spring-dashpot unit is equal to the absolute displace-

ment x of the mass. Assuming the system to be initially in equilibrium (

δ=0, δ=0),

Eq. (31.6) is solved for extreme values of δ and F(

δ,δ) since F is a known function of

time. These are to be compared with the displacement and force limitations of the

shock isolator. Often the supporting structure is sufficiently rigid that the maximum

force in the isolator may be considered as a force applied statically to the support.

Then the foregoing analysis is adequate for determining the stress in the support.

The load on the floor may be treated as dynamic instead of static by a simple

analysis if the displacement and velocity of the support are negligible in comparison

with those of the equipment. Consider the system of Fig. 31.3B where the support-

ing structure is represented as a mass m

and a spring-dashpot unit in place of the

rigid support shown in Fig. 31.3A. The force acting on the supporting structure is a

known function of time F(

δ,δ) as found from the previous solution of Eq. (31.6).

To find the maximum force within the support structure requires a solution of an

equation analogous to Eq. (31.6) where

is substituted for

δ, m

for m, F

(

,δ

) for

δ,δ), and F(

δ,δ) for F. For engineering purposes it suffices to find the extreme val-

ues of δ

and F

(

,δ

). The first is needed to verify the assumption that support

motion is negligible compared with equipment motion, and can be used to determine

the maximum stress in the support. The second is the maximum force applied by the

support structure to its base.

MATHEMATICAL EQUIVALENCE OF CLASS I

AND CLASS II PROBLEMS

The similarity of shock isolation principles in Class I and Class II is indicated by the

similar form of Eqs. (31.5) and (31.6). The right-hand side (−mü or F) is given as a

function of time, and the extreme values of δ and F(

δ,δ) are desired.When the actual

THEORY OF SHOCK ISOLATION 31.5

FIGURE 31.3 Idealized systems showing use of isolator with transmitted force F(

δ,δ) to reduce

force transmitted to foundation when force F is applied to equipment of mass m. In (A) the founda-

tion is rigid and in (B) it has mass m

and stiffness damping characteristics F

(

,δ

8434_Harris_31_b.qxd 09/20/2001 12:33 PM Page 31.5