Heinrich J.G., Aldinger F. (Eds.) Ceramic Materials and Components for Engines

Подождите немного. Документ загружается.

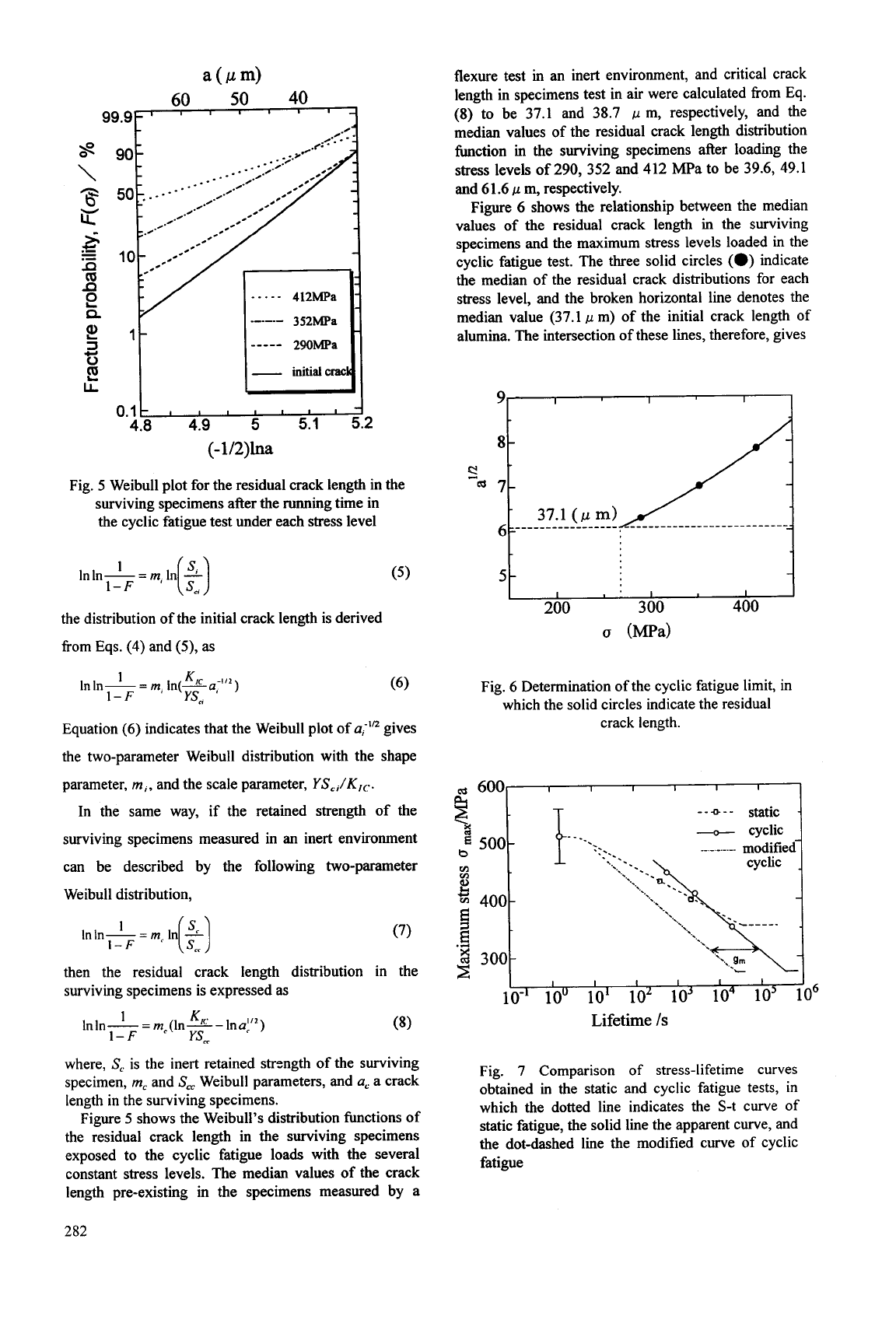
99.9-

0.lL

‘1

‘

‘-I

4.8

4.9

5.1

5.2

(-1/2)lna

Fig.

Weibull plot for the residual crack length in the

surviving specimens after the running time in

the cyclic fatigue test under each stress level

Inln-=m,

In(?)

the distribution of the initial crack length is derived

from Eqs.

(4)

and

(9,

Equation (6) indicates that the Weibull plot of

u;’”

gives

the two-parameter Weibull distribution with the shape

parameter,

m,,

and the scale parameter,

YS,,/K,,.

In the same way, if the retained strength of the

surviving specimens measured in an inert environment

can be described by the following two-parameter

Weibull distribution,

(7)

then the residual crack length distribution in the

surviving specimens is expressed

where,

is the inert retained strzngth of the surviving

specimen,

and

S,,

Weibull parameters, and

a crack

length in the surviving specimens.

Figure

shows the Weibull’s distribution functions of

the residual crack length in the surviving specimens

exposed to the cyclic fatigue loads with the several

constant stress levels. The median values of the crack

length pre-existing in the specimens measured by a

flexure test

an inert environment, and critical crack

length in specimens test in air were calculated from Eq.

(8)

to be 37.1 and 38.7

m, respectively, and the

median values of the residual crack length distribution

function in the surviving specimens after loading the

stress levels

290, 352 and 412 MPa to be 39.6, 49.1

and

1.6

m, respectively.

Figure

shows the relationship between the median

values of the residual crack length in the surviving

specimens and the maximum stress levels loaded in the

cyclic fatigue test. The three solid circles

(0)

indicate

the median of the residual crack distributions for each

stress level, and the broken horizontal line denotes the

median value (37.1

m) of the initial crack length of

alumina. The intersection of these lines, therefore, gives

Fig. 6 Determination of the cyclic fatigue limit, in

which the solid circles indicate the residual

crack length.

Fig.

Comparison of stress-lifetime curves

obtained in the static and cyclic fatigue tests, in

which the dotted line indicates the S-t curve of

static fatigue, the solid line the apparent curve, and

the dot-dashed line the modified curve of cyclic

fatigue

282

the fatigue limit of alumina under cyclic fatigue loads

which was calculated to be

270

MPa, because no crack

extension is expected under the stress level.

The same technique is applicable to the estimation of

the static fatigue limit, which will be presented

elsewhere[9]. The ratio of the fatigue limit to the flexure

strength in air was calculated

0.71 for the static

fatigue and 0.53 for the cyclic fatigue.

Figure 7 shows the complete S-t curves obtained in

the static and cyclic fatigue tests, in which the empty

squares

(0)

indicate the median of the distribution of

the static fatigue lifetimes, the empty circles

(0)

the

median of the distribution of the apparent cyclic fatigue

lifetimes, and the dot-dashed line the modified S-t curve

in the cyclic fatigue test calculated using the following

g, modification[ 151.

(9)

where

max

is the maximum stress of cyclic wave,

the cyclic stress and

the cyclic period. By

comparing the static and modified cyclic curves, it is

apparent that the difference between them in the figure

is relatively small at higher stress levels, but more

significant at lower stress levels. This suggests that at

higher stress levels, cracks propagate

quickly that the

cyclic effects will not be sufficient to reduce the stress

shielding by bridging and/or interlocking on the process

zone wake. In addition, at higher stress levels, the

time-dependent mechanism of cyclic fatigue due to an

environmentally enhanced crack growth is predominant,

and the difference between the lifetimes in the static and

cyclic fatigue tests becomes small. On the other hand, at

lower stress levels, the rate of the crack extension

caused by cyclic fatigue loading is

low that the

bridging at the process zone wake is extensively

weakened due to the cyclic stress, which accelerates the

crack extension. Hence, the difference between the

lifetimes in the static and cyclic fatigue tests becomes

larger. It is also evident that stress corrosion cracking

plays no role in the determination of the cyclic fatigue

limit because the cyclic fatigue limit is obviously lower

than the static fatigue limit. Figure 7 indicates that there

are mainly two crack extension mechanisms in alumina

ceramics under a cyclic fatigue load, the one is time-

dependent crack extension caused by stress corrosion

cracking, the other is cycle-dependent crack extension

caused by degradation of stress shielding in process

zone wake.

CONCLUSION

Static and cyclic fatigue tests were performed on

99.5% pure alumina of moderate grain size (about 2

using smooth-surface specimens under several stress

levels.

statistical treatment, including imperfect data,

was used to estimate the original distributions of fatigue

lifetimes.

technique for estimating the static and

cyclic fatigue limits defined upon a statistical aspect

was also proposed using the relationship between the

residual crack length in the specimens surviving after

the running time and the stress level loaded. The results

revealed that the ratio of the fatigue limit to the flexure

strength in air was 0.53 for the cyclic fatigue and 0.71

for the static fatigue. The statistical technique for

estimating the fatigue limits proposed here was simple

and quite reasonable compared with other techniques

which require a large number of specimens and are

time-consuming.

REFERENCES

(1)

Horibe and R. Hirata, Cyclic Fatigue of Ceramic

Materials: Influence of Crack Path and Fatigue

Mechanisms, Acta Metall. Mater., 39 (1991) 1309-

1317.

(2) D.

Jacobs and Lwei Chen, Mechanical and

Environmental Factors in the Cyclic and Static

Fatigue of Silicon Nitride,

Am. Ceram. SOC., 77

(3) H. Kishimoto, A. Ueno and H. Kawamoto, Crack

Propagation Characteristics of Sintered Si,N, under

Static and Cyclic Loads, 3. SOC. Mater. Sci. Japan,

36 (1987) 1122-1127 (in Japanese).

(4) R. H. Dauskardt, W. Yu and R.

Richie, Fatigue

Crack Propagation in Transformation-Toughened

Zirconia Ceramic, J. Am. Ceram. SOC., 70 (1987)

(5)

H. Dauskardt, A Frictional-Wear Mechanism for

Fatigue-Crack Growth in Grain Brdging Ceramics,

Acta Metall. Mater., 4 1

993) 2765-278 1.

(6)

D. A. Krohn and D. P.

Hasselman, Static and

Cyclic Fatigue Behavior of a Polycrystalline

Alumina, J. Am. Ceram. SOC.,

(1972) 208-211.

(7)

Awaji,

Yamamoto,

Honda and T. Nishikawa,

Static and Cyclic Stress-Lifetime Curves

Ceramics,

Mat. Sci. Letters 19 (2000) 713-715.

(8)

Jin, A. Honjyo and H. Awaji, Static and Cyclic

Fatigue Limits of Alumina Ceramics, J. Ceram. SOC.

Japan 108 (2000) 614-617.

(9) T. Sakai and K. Fujitani,

Statistical Aspect on

Fatigue Behavior of Alumina Ceramics in Rotating

Bending, Engng. Fract. Mech., 32 (1989) 653-664.

(10) B. J.

Wilkins and

Dutton, Static Fatigue Limit

with Particular Reference to Glass, J. Am. Ceram.

Awaji and Y. Sakaida, V-Notch Technique for

Single-Edge Notched Beam and Chevron Notch

Methods, J. Am. Ceram. SOC., 73 (1990) 3522-3523.

(12)

Awaji, T. Watanabe,

Sakaida and

Nakagawa, Fracture Toughness Measurements

Ceramics by N Notch Technique, Ceramics Int., 18

(13)

Ohya and K. Ogura, Cyclic Fatigue Testing

Device for Fine Ceramics by Using Piezo-electric

Bimorph Actuator, J. SOC. Mater. Sci. Japan, 38

(14) D. Munz and T. Fett, Ceramics, Springer-Verlag,

(15)

A. G. Evans and E. R. Fuller, Metal. Trans.,

(

994) 1

53-

1 6

C248-252.

SOC., 59 (1976) 108-112.

(1992) 11-17.

(1989) 44-48.

Berlin

999) 89-9

(1974) 27-33.

283

This Page Intentionally Left Blank

LIFETIME PREDICTION OF CERAMIC THERMAL BARRIER COATINGS

BASED ON LIFETIME ANALYSES OF CLOSE TO REALITY TESTS

Bartsch",

Marci,

Mull, Ch. Sick

German Aerospace Center (DLR), Institute for Materials Research,

D-51147

Koln, Germany

ABSTRACT

A lifetime prediction concept for thermal barrier

coatings (TBC) based on lifetime analyses of close to

reality tests is given. Basic idea is to ensure that failure

mechanisms during testing are the same as under service

conditions in an engine. Since, it is impractical to

simulate service load cycles of about at least one hour in

real-time, number of cycle dependent fatigue damages

and time-at-high-temperature dependent damages by

kinetic mechanisms are imposed separately. With a

newly built testing facility the cyclic load of an aircraft

engine service cycle is simulated but with drastically

reduced holding times.

First test results on specimens with an electron beam

physical vapour deposited (EB-PVD) TBC exhibit that

the as-coated properties of the ceramic coating are

sufficient to survive the fatigue loading under service

conditions. The influence of kinetic damage

mechanisms on the TBC-lifetime will be determined in

tests with pre-aged specimens.

INTRODUCTION

In advanced gas turbines for aircraft engines

electric power generation, internally cooled turbine

blades are coated with

ceramic thermal barrier to

reduce the thermal load of the metallic substrate.

Exhausting the full potential of the ceramic thermal

barrier coating to increase the turbine inlet temperature

(TIT) requires reliable lifetime prediction methods,

since after failure of the TBC the remaining lifetime of

the blade will be extremely short.

The thermal barrier coating system

The commonly used TBC material is yttria stabilised

zirconia applied by electron beam physical vapour

deposition (EB-PVD) or plasma spraying (PS). Zirconia

TBCs are applied on airfoil surfaces coated with a

metallic corrosion resistant layer which imparts good

adhesion for the TBC on the substrate. This

called

bond coat (BC) consists frequently of MCrAlY- or

PtA1-alloys.

The thermal conductivity of zirconia TBCs is

relatively low and depends on the deposition process.

Plasma sprayed coatings have initial values for the

thermal conductivity between

0.8

and 1.2Wm-'K-' while

EB-PVD TBCs have somewhat higher conductivity of

1.5-1.8Wm-'R1[1]. Due to the low thermal conductivity

zirconia coatings of about 150-300pm thickness

maintain a temperature drop of 60" to 17OOC from the

hot gas to the metallic substrate under stationary

conditions, depending on the heat flux in the turbine

engine [2, 31. The temperature gradient across the wall

of a coated and internally cooled turbine blade is

schematically shown in Fig. 1. As additional important

effect TBCs decrease the temperature transients, that

means the thermal shock load,

the metallic substrate

during start and shut down of the engine.

Temperature

100°C

Ceramic Metallic

Hot

Gas

Substrate

Gas

Film

Bond

Coat

Fig. 1. Thermal gradient across the wall of an internally

cooled turbine blade with TBC

Stresses by thermal mismatch between TBC and

nickel- based super-alloy substrates are relatively low

due to the similar thermal expansion coefficient which

is at max. service temperature about 9-1 1.

for the

TBC and 14

16.10-6K-' for the substrate. The initially

Young's-modulus

zirconia TBC is reasonably low

with about only 35

60 GPa

[4,

and supplies high

tolerance against straining and thermal shock.

Damage mechanisms

Under service conditions the properties of the TBC-

system change. Progressive damages are caused by

stresses in and between the different layers

the TBC

system, generated by the complex thermal and

mechanical cyclic loading and the mismatch of several

physical properties of the substrate and the coating

materials. During the lifetime of a TBC system, local

loading conditions and resistance against damage and

failure change by reason of changing physical properties

of the individual layer materials. For example,

densification of the ceramic topcoat by sintering leads to

increased Young's-modulus and thus decreased strain

tolerance. Thermal cycling above 1200°C cause phase

transformations from partially stabilised tetragonal

285

zirconia to monoclinic phase resulting in volume

changes and hence increase of local stresses

[6,

71.

significant portion of residual stresses perpendicular to

the coated surface develops due to the growth of the

oxide scale (TGO) on the bond coat. Diffusion of alloy

elements and impurities from the substrate to the

interface between bond coat and ceramic reduces the

adhesion of the TBC [8].

The failure criterion of the TBC is defined as

spallation of the TBC from the substrate since the

function of the thermal barrier is impaired most

seriously by local

loss

of the TBC. Spallation within the

ceramic topcoat is called ‘white failure’. If the

separation of the TBC propagates within the TGO or at

the interface between TGO and BC it is called ‘black

failure’. White failure is more often observed in PS

coatings and highly dependent on interfacial roughness

with evidence to slow (subcritical) micro-crack growth,

crack linking and eventual buckling

[9,

lo]. Black

failures are dependent on the extend of bond coat-

oxidation and frequently related to EB-PVD-coatings

with their typical smooth interface between TGO and

bond coat.

The damage mechanisms and their interaction

leading to spallation of the TBC, whether

PS-

or EB-

PVD processed, are not well understood. Generally we

can distinguish between fatigue mechanisms, which are

number-of-cycle dependent and kinetic mechanisms

depending on time-at-high-temperature. Which

mechanisms are dominating and which synergy effects

are working depends on the materials parameter of the

certain coating system and the service conditions. For

example in aircraft engines the maximum temperature

during one service cycle is higher than in stationary gas

turbines while the time at high temperature is longer in

the latter.

Lifetime prediction concept

For TBC lifetime prediction in [4, 11,121 Manson-

Coffin type damage accumulation rules were developed

which base on empirical damage parameters related to

certain damage mechanisms. Kinetics and dependence

of cyclic loading of the damage parameters are

determined separately in simplified experiments.

Subsequently the contribution of every damage

mechanism to the consumption of initial lifetime under

more realistic testing conditions will be accumulated.

For example

[4] as time-at-high-temperature

dependent damage parameter the thickness of the TGO

is set in relation to the degree of damage due to the

mechanism ‘oxidation of the bond coat’. Kinetics of

TGO-growth is determined in oxidation experiments.

The decrease of number of thermal cycles to failure due

to TGO-growth was calculated with the cumulative

damage rule for burner rig tests and experimentally

verified.

However, service conditions are quite more complex

and consequently the number of parameters which have

to be taken into account for estimating the TBC lifetime

is reasonably high. Additional fitting parameters are

needed to include interaction effects of the different

mechanisms. The required high number of parameters

needed to describe the damage situation makes this

concept impractical for lifetime prediction under service

conditions.

Instead of accumulating the contributions of separate

damage mechanisms determined under simplified

testing conditions our idea is to make the testing

conditions as realistic as possible. Thus, we ensure that

the damage mechanisms including interaction effects

are identical to that under service conditions [13, 141.

However, it is impractical to simulate a service cycle in

real time since, turbine blades in modern gas turbines

are designed for about 20.000h in the case of aircraft

engines and up to 50.000h for stationary engines. The

time

one test cycle can be decreased drastically if we

determine number-of-cycle dependent fatigue damages

separate from damages by kinetic mechanisms because

fatigue damages

are

induced by changes of the load and

not by the holding time

a certain load level. Damages

induced by time-at-high-temperature dependent kinetic

mechanisms will be considered by testing heat-treated

specimens.

EXPERIMENTAL

Requirements for realistic test cycle

Under service conditions coated turbine blades are

loaded simultaneously by thermal and superposed

mechanical cycling. The thermal and the mechanical

load depend on the blade location. E.g. in rotor blades

the mechanical load due to centrifugal forces increases

from

the

blades tip

the blades fillet while the thermal

load at the fillet is the lowest. With simple thermal

cycling we are not able

simulate variable straining at

a certain temperature since the strain amplitude due to

thermal cycling is a function of the temperature

difference. The strain of the compound of metallic

substrate and TBC-system is compulsorily identical

over the cross section. The strain compulsion

consequently entails a complex stress distribution over

the cross section due to the different physical properties

of the single materials and the thermal gradient over the

cross section. The stress distribution for the same strain

is quite different under isothermal conditions and in a

thermal gradient respectively. Since, the stress

amplitudes at the failure location of the TBC-system are

the driving force for the TBC-failure, it is necessary to

impose a realistic temperature gradient during testing.

On the other hand the temperature gradient has

consequences for kinetic damage mechanisms because

the time constants of kinetic mechanisms depend on the

temperature.

Testing facility and load cycle

A testing facility was built which simulates closely

the conditions for a gas turbine blade, i.e. cycles with

simultaneous mechanical and thermal loading, including

thermal shock and temperature gradients over the cross

section of the specimens. Hollow cylindrical specimens

with a metal substrate wall of 2 mm, similar to the

typical geometry of the convex side of a turbine blade

near the leading edge, are tested.

sketch of the

specimen is shown in Fig.

286

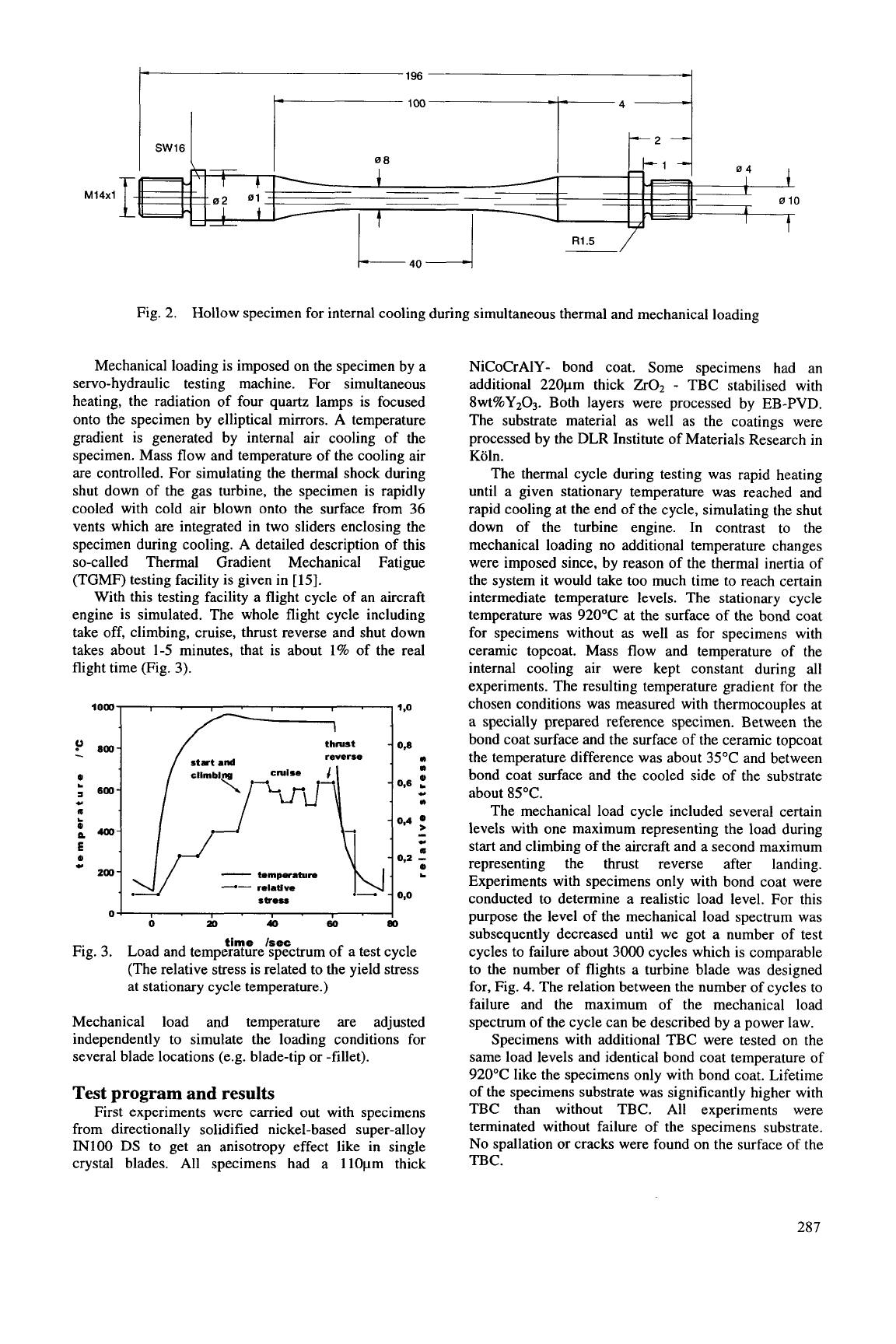
M14x1

Fig.

Hollow specimen for internal cooling during simultaneous thermal and mechanical loading

Mechanical loading is imposed on the specimen by a

servo-hydraulic testing machine. For simultaneous

heating, the radiation of four quartz lamps is focused

onto the specimen by elliptical mirrors.

temperature

gradient is generated by internal air cooling of the

specimen. Mass flow and temperature of the cooling air

are controlled. For simulating the thermal shock during

shut down of the gas turbine, the specimen is rapidly

cooled with cold air blown onto the surface from

vents which are integrated in two sliders enclosing the

specimen during cooling.

detailed description of this

so-called Thermal Gradient Mechanical Fatigue

(TGMF) testing facility is given in

[

151.

With this testing facility a flight cycle of an aircraft

engine is simulated. The whole flight cycle including

take off, climbing, cruise, thrust reverse and shut down

takes about 1-5 minutes, that is about

of the real

flight time (Fig. 3).

tempwature

,JJ

relative

rbeu

Fig. 3. Load and temperature spectrum of a test cycle

(The relative stress is related to the yield stress

at stationary cycle temperature.)

time

lsec

Mechanical load and temperature are adjusted

independently to simulate the loading conditions for

several blade locations (e.g. blade-tip

-fillet).

Test

program

and

results

First experiments were carried out with specimens

from directionally solidified nickel-based super-alloy

IN100

to get an anisotropy effect like in single

crystal blades. All specimens had a llOpm thick

NiCoCrAIY- bond coat. Some specimens had an

additional 220pm thick

ZrOz

TBC stabilised with

8wt%Y203.

Both layers were processed by EB-PVD.

The substrate material as well as the coatings were

processed by the DLR Institute of Materials Research

Koln.

The thermal cycle during testing was rapid heating

until a given stationary temperature was reached and

rapid cooling at the end of the cycle, simulating the shut

down of the turbine engine. In contrast to the

mechanical loading no additional temperature changes

were imposed since, by reason of the thermal inertia of

the system it would take too much time to reach certain

intermediate temperature levels. The stationary cycle

temperature was 920°C at the surface of the bond coat

for specimens without as well as for specimens with

ceramic topcoat. Mass flow and temperature of the

internal cooling air were kept constant during all

experiments. The resulting temperature gradient for the

chosen conditions was measured with thermocouples at

a specially prepared reference specimen. Between the

bond coat surface and the surface of the ceramic topcoat

the temperature difference was about 35°C and between

bond coat surface and the cooled side of the substrate

about 85°C.

The mechanical load cycle included several certain

levels with one maximum representing the load during

start and climbing of the aircraft and a second maximum

representing the thrust reverse after landing.

Experiments with specimens only with bond coat were

conducted to determine a realistic load level. For this

purpose the level of the mechanical load spectrum was

subsequently decreased until we got a number of test

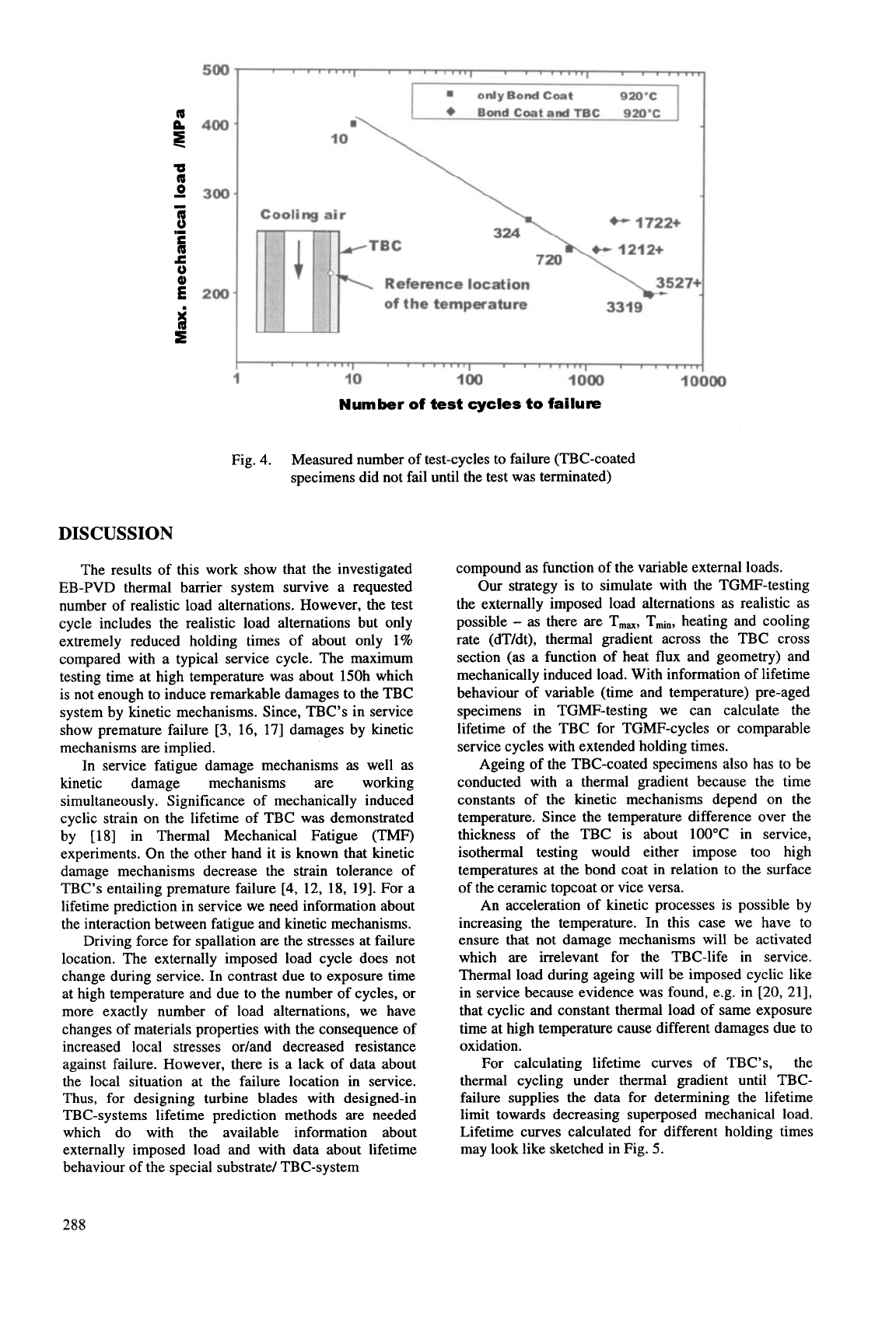
cycles to failure about

3000

cycles which is comparable

to the number of flights a turbine blade was designed

for, Fig.

The relation between the number

cycles to

failure and the maximum of the mechanical load

spectrum of the cycle can be described by a power law.

Specimens with additional TBC were tested on the

same load levels and identical bond coat temperature of

920°C like the specimens only with bond coat. Lifetime

of the specimens substrate was significantly higher with

TBC than without TBC. All experiments were

terminated without failure of the specimens substrate.

spallation

cracks were found on the surface of the

TBC.

287

onlyBondCoat 920-c

BondCogtandTBC 92O’C

Cooling

air

+--

1722+

Reference location

the temperature

3319

I I

10 100

000

Number

test

cycles

failure

Fig.

Measured number of test-cycles to failure (TBC-coated

specimens did not fail until the test was terminated)

DISCUSSION

The results of this work show that the investigated

EB-PVD thermal barrier system survive a requested

number of realistic load alternations. However, the test

cycle includes the realistic load alternations but only

extremely reduced holding times of about only 1%

compared with a typical service cycle. The maximum

testing time at high temperature was about 150h which

is not enough to induce remarkable damages to the TBC

system by kinetic mechanisms. Since, TBC’s in service

show premature failure

[3,

16,

171 damages by kinetic

mechanisms are implied.

In service fatigue damage mechanisms as well as

kinetic damage mechanisms are working

simultaneously. Significance of mechanically induced

cyclic strain on the lifetime of TBC was demonstrated

by [18] in Thermal Mechanical Fatigue

(TMF)

experiments. On the other hand it is known that kinetic

damage mechanisms decrease the strain tolerance of

TBC’s entailing premature failure

[4,

12, 18, 191. For a

lifetime prediction in service we need information about

the interaction between fatigue and kinetic mechanisms.

Driving force for spallation are the stresses at failure

location. The externally imposed load cycle does not

change during service. In contrast due to exposure time

at high temperature and due to the number of cycles, or

more exactly number of load alternations, we have

changes of materials properties with the consequence of

increased local stresses or/and decreased resistance

against failure. However, there is a lack of data about

the local situation at the failure location in service.

Thus, for designing turbine blades with designed-in

TBC-systems lifetime prediction methods are needed

which do with the available information about

externally imposed load and with data about lifetime

behaviour of the special substrate/ TBC-system

compound as function of the variable external loads.

Our strategy is to simulate with the TGMF-testing

the externally imposed load alternations as realistic as

possible

as there are T,,, Tmi,, heating and cooling

rate (dT/dt), thermal gradient across the TBC cross

section (as a function of heat flux and geometry) and

mechanically induced load. With information of lifetime

behaviour of variable (time and temperature) pre-aged

specimens in TGMF-testing we can calculate the

lifetime of the TBC for TGMF-cycles or comparable

service cycles with extended holding times.

Ageing of the TBC-coated specimens also has to be

conducted with a thermal gradient because the time

constants of the kinetic mechanisms depend on the

temperature. Since the temperature difference over the

thickness of the TBC is about 100°C in service,

isothermal testing would either impose too high

temperatures at the bond coat in relation to the surface

of the ceramic topcoat or vice versa.

An acceleration of kinetic processes is possible by

increasing the temperature. In this case we have

ensure that not damage mechanisms will be activated

which are irrelevant for the TBC-life in service.

Thermal load during ageing will be imposed cyclic like

in service because evidence was found, e.g. in [20, 211,

that cyclic and constant thermal load of same exposure

time at high temperature cause different damages due to

oxidation.

For calculating lifetime curves of TBC’s, the

thermal cycling under thermal gradient until TBC-

failure supplies the data for determining the lifetime

limit towards decreasing superposed mechanical load.

Lifetime curves calculated for different holding times

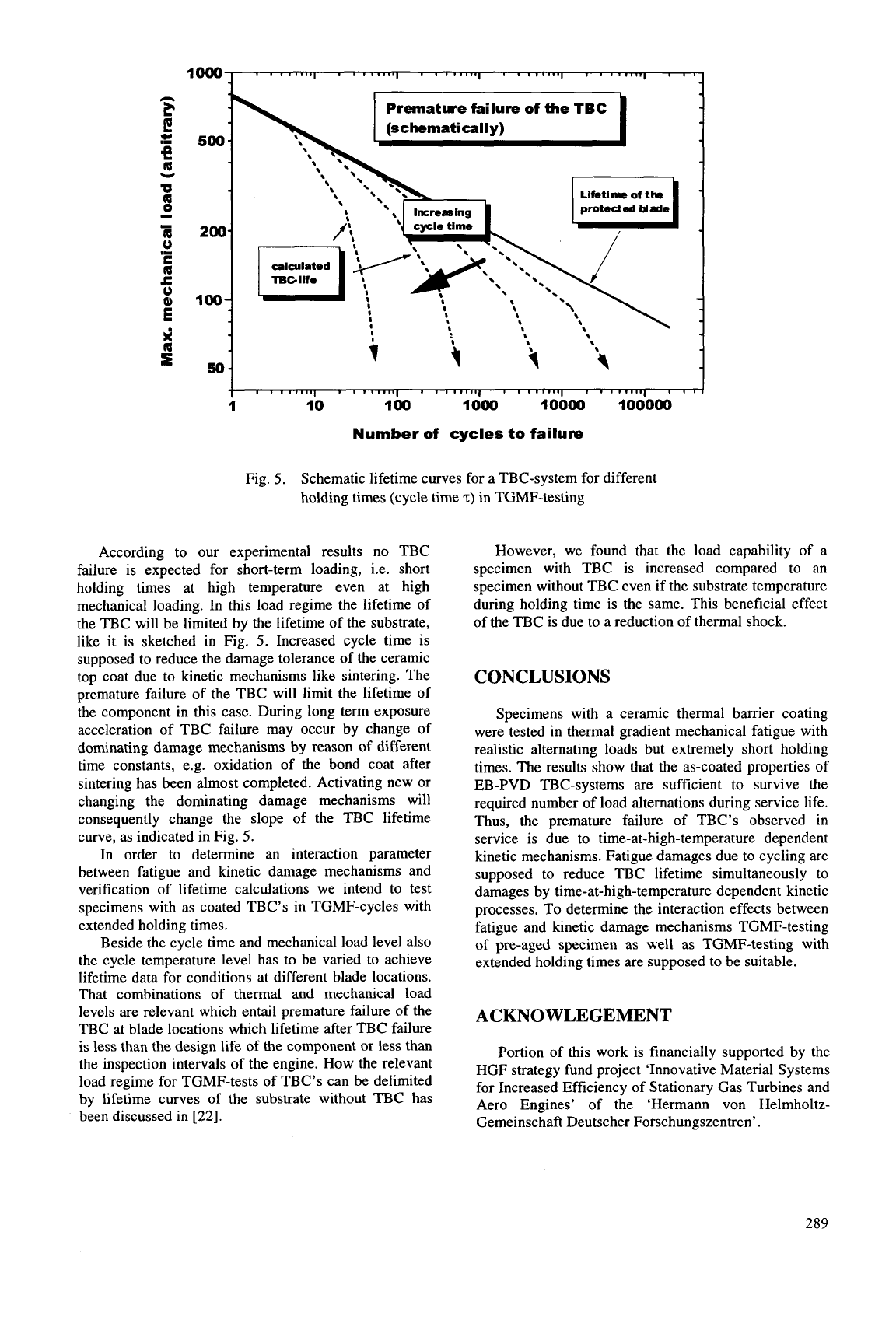
may look like sketched in Fig.

288

000

;t:

500-

200-

100-

;

50-

Fig.

Schematic lifetime curves for a TBC-system for different

holding times (cycle time

in TGMF-testing

' '

"""I

' '

"""I

' '

"""I

' '

""'I

' '

""'I

' '

""'I

' '

100

1000

IOOW

100000

According to

our

experimental results no TBC

failure is expected for short-term loading, i.e. short

holding times at high temperature even at high

mechanical loading. In this load regime the lifetime of

the TBC will be limited by the lifetime of the substrate,

like it is sketched in Fig.

Increased cycle time is

supposed to reduce the damage tolerance of the ceramic

top coat due to kinetic mechanisms like sintering. The

premature failure of the TBC will limit the lifetime of

the component in this case. During long term exposure

acceleration of TBC failure may occur by change of

dominating damage mechanisms by reason of different

time constants, e.g. oxidation

the bond coat after

sintering has been almost completed. Activating new

changing the dominating damage mechanisms will

consequently change the slope of the TBC lifetime

curve, as indicated in Fig.

order to determine an interaction parameter

between fatigue and kinetic damage mechanisms and

verification of lifetime calculations we inte.nd to test

specimens with as coated TBC's in TGMF-cycles with

extended holding times.

Beside the cycle time and mechanical load level also

the cycle temperature level has to be varied to achieve

lifetime data for conditions at different blade locations.

That combinations

thermal and mechanical load

levels are relevant which entail premature failure of the

TBC at blade locations which lifetime after TBC failure

is less than the design life of the component

less than

the inspection intervals of the engine. How the relevant

load regime for TGMF-tests of TBC's can be delimited

by lifetime curves

the substrate without TBC has

been discussed in

[22].

However, we found that the load capability of a

specimen with TBC is increased compared to an

specimen without TBC even

the substrate temperature

during holding time is the same. This beneficial effect

of the TBC is due to a reduction of thermal shock.

CONCLUSIONS

Specimens with a ceramic thermal barrier coating

were tested

thermal gradient mechanical fatigue with

realistic alternating loads but extremely short holding

times. The results show that the as-coated properties of

EB-PVD TBC-systems are sufficient to survive the

required number of load alternations during service life.

Thus, the premature failure of TBC's observed in

service is due to time-at-high-temperature dependent

kinetic mechanisms. Fatigue damages due to cycling are

supposed to reduce TBC lifetime simultaneously to

damages by time-at-high-temperature dependent kinetic

processes. To determine the interaction effects between

fatigue and kinetic damage mechanisms TGMF-testing

of pre-aged specimen as well as TGMF-testing with

extended holding times are supposed to be suitable.

ACKNOWLEGEMENT

Portion of this work is financially supported by the

HGF strategy fund project 'Innovative Material Systems

for Increased Efficiency of Stationary Gas Turbines and

Aero Engines' of the 'Hermann von Helmholtz-

Gemeinschaft Deutscher Forschungszentren'

289

REFERENCES

[

121 J.T. DeMasi, K.D. Scheffler, M.Ortiz, Thermal

Barrier Coating Life Prediction Model

Development, Phase

NASA Contractor Report

182230, United Technologies Corp., Pratt

Whitney, (1989).

131 W. A. Kaysser and M. Bartsch, Fatigue of

Thermal Barrier Coatings, Proceedings of the 7*

international conference Fatigue’99, P.R. China,

Beijing June 8-12, 1999, ed. X.R. Wu

Z.G.

141 M. Bartsch, G. Marci,

Mull, Ch. Sick, Fatigue

Testing of Ceramic Thermal Barrier Coatings for

Gasturbine Blades, Advanced Engineering

Materials, 2

[ll]

(1999) 127-129.

[15] G. Marci,

M. Mull, Ch. Sick, M. Bartsch, New

Testing Facility and Concept for Life Prediction

of TBC Turbine Engine Components, 3”

Symposium on Thermo-Mechanical Fatigue

Behavior of Materials, 4.-5. Nov 1998, Norfolk,

Virginia, ASTM

STP

1371, (2000) 296-303.

[16]

Mutasim and W. Brentnall, Proc. ‘Thermal

Barrier Workshop’ March 27-29, NASA Conf.

[17] M. Arana, J. Goedjen, Perspectives on TBC Life

Prediction for Industrial Gas Turbines,

Proceeding of the TBC Winterworkshop, Jan. 6-8,

University of California, Santa Barbara, (1999).

[

181 P.K. Wright, Influence of cyclic strain on life of a

PVD

TBC,

Mat. Sci. Engineering A245, (1998)

[19] R. Herzog,

Schubert, L. Singheiser, The

influence of substrate deformation on the damage

of a TBC compound under thermomechanical

loading, Proccedings of Euromat 99, 27-30 Sept.

1999, Miinchen, (2000), in press.

[20] M. Schutze, Materials and Corrosion 47, (1996)

103-105. (in german)

[21] M. Schiitze, Protective oxide scales and their

break down, John Wiley

sons, Cichester, UK,

(1997).

[22] M. Bartsch, G. Marci,

Mull, Ch. Sick, Lifetime

Prediction for Ceramic Thermal Barrier Coatings,

Proceedings of the Euromat’99 Conference

27.-

30. Sept. 1999, Munchen, Volume 11, Surface

Engineering (ed.: H. Dimigen), (2000) 25-30.

Wag, Vol. 3, (1999) 1897-1904.

Publ. 3312, (1995) 103-112.

19 1-200.

R.B. Dinwiddie, S.C. Beecher, W.D. Porter, B.A.

Nagaraj, ASME-Report 96-GT-282, (1996).

G.W. Goward, Surface and Coatings Technology,

A. Mariccochi, A. Bartz, and D. Wortmann, Proc.

‘Thermal Barrier Workshop’ March 27-29,

NASA Conf. Publ. 3312, (1995) 79-89.

S.M. Meier, D.M. Nissley, K.D. Sheffler,

,,Thermal Barrier Coating Life Prediction Model

Development“, Phase

11,

Final Report, NASA

Contractor Report 1891 11, United Technologies

Corp., Pratt

Whitney, (1991)

G. Marci, M. Bartsch,

Mull, Determination of

the Young’s modulus of TBC-materials for

thermally and mechanically highly loaded

components in gas turbines, (in german) DVM-

Bericht “Werkstoffpriifung 1999“, 2.13. Dez. ‘99,

Bad Nauheim, (1999) 271-280.

U. Schulz, Phase Transformation in EB-PVD

Yttria Partially Stabilized Zirconia Thermal

Barrier Coatings during Annealing, J. Am.

Ceram. SOC., 83 [4] (2000) 904-910.

L. Lelait,

Alperine, C. Diot, R. Mevrel,

’Thermal Barrier Coatings: Microstructural

Investigation after Annealing‘, Mater. Sci. Eng. A,

U. Kaden, C. Leyens, M. Peters, W.A. Kaysser,

Thermal Stability of an EB-PVD Thermal Barrier

Coating System on a Single Crystal Nickel-Base

Superalloy, in

Elevated Temperature Coatings:

Science and Technology 111, J.M. Hampikian

N.B. Dahotre (Hrsg.), TMS, (1999) 27-38.

A.G. Evans, J.W. Hutchinson, On the Mechanics

of Delamination and Spalling in Compressed

Films, Int. J. Solids Structures, Vol. 20, No.

108-109, (1998) 73-79.

A121, (1991) 475-82.

(1984) 455-466.

[lo] M.Y. He, A.G. Evans, J.W. Hutchinson,

Effects of morphology on the decohesion of

compressed thin films, Mat. Sci. Engineering

[

113 R.A. Miller, Oxidation-Based Model for Thermal

Barrier Coating Life,

Am. Ceram. SOC., 67 [8]

A245, (1998) 168-181.

(1984) 517-521.

290

CREEP OF A SILICON NITRIDE UNDER VARIOUS SPECIMEN/LOADING

CONFIGURATIONS

Sung R. Choi, Lynn M. Powers, Frederic A. Holland, and John P. Gyekenyesi

NASA Glenn Research Center, Cleveland, Ohio

44135,

USA

ABSTRACT

Extensive creep testing of a hot-pressed silicon

nitride (NC132) was performed at 1300°C in air using

five different specimenlloading configurations,

including pure tension, pure compression, four-point

uniaxial flexure, ball-on-ring biaxial flexure, and ring-

on-ring biaxial flexure. Nominal creep strain and its

rate for a given nominal applied stress were greatest in

tension, least in compression, and intermediate in

uniaxial and biaxial flexure. Except for the case of

compressive loading, nominal creep strain generally

decreased with time, resulting in less-defmed steady-

state condition. Of the four different creep formulations

power-law, hyperbolic sine, step, and redistribution

models

the conventional power-law model provides

the most convenient and reasonable means to estimate

simple, quantitative creep parameters of the material.

Predictions of creep deformation for the case of

multiaxial stress state (biaxial flexure) were made based

on pure tension and compression creep data by using the

design code CARESICreep.

INTRODUCTION

Advanced ceramics are candidate materials for high-

temperature structural applications in gas turbine

engines and heat recovery systems. The

two

major

limitations

these materials, slow crack growth and

creep, are generally encountered in high-temperature

applications. At higher temperatures, particularly at

lower applied stress, enhanced creep takes place in the

form of permanent deformation and/or damage

accumulation, leading to loss of structural integrity and

possibly the eventual rupture of components.

Therefore, for higher-temperature applications, the

accurate determination of creep behavior including

creep and rupture parameters and associated

mechanisms is important for ensuring structural

integrity and component life.

Because of difference in

creep between tension and compression

[

1-31,

parameters that are derived from relatively easy flexural

testing using the conventional simple beam theory,

which assumes the neutral axis to be fixed, can be

misleading.

Many structural components are subjected

to multiaxial stresses, typically combined with tensile

and compressive stresses. Therefore, in order to

accurately predict or estimate creep deformation and

rupture of multiaxially stressed components, creep and

rupture parameters of a material should be determined

individually both in tension and in compression,

together with an appropriate predictionldesign

methodology.

The immediate objective of this work was to

develop and conduct creep testing to determine creep

behavior of a hot-pressed silicon nitride under various

loading configurations at 1300°C in air. The loading

configurations used in this study include pure tension,

pure compression, four-point uniaxial flexure, ball-on-

ring biaxial flexur

e, and ring-on-ring biaxial flexure. Creep displacements

for each specimenlloading configuration were

determined as a function of time with several different

levels of applied loads. NASA Glenn Research Center

has developed an analytical methodology and an

integrated design program named CARESICreep

(Ceramics Analysis and Reliability Evaluation of

Structureslcreep) to be used for predicting the creep

deformation and rupture life of structural ceramic

components

[4,5].

The second objective of this work

was to validate the CARESICreep design code on the

basis of the creep database generated from the

experimental work. This was done by predicting creep

deformation subjected to multiaxial (biaxial) stress state

based on the basis of pure tension and pure compression

data and by comparing with actual biaxial flexure data.

EXPERIMENTAL PROCEDURES

The material used in this work was a hot-pressed

silicon nitride (designated as NC132, Vintage 1990,

fabricated by Norton Co., Northboro,

MA)

containing

MgO as primary sintering aid. This material was

chosen since it has shown for decades a controlled

uniformity in mechanical and physical properties such

as hardness, fracture toughness, strength, and slow crack

growth, etc.

The material also has been extensively

characterized previously to determine fatigue andlor

creep life prediction parameters as a candidate gas

turbine material

[6-81.

Creep testing was performed in dead-weight creep

frames (Applied Testing Systems, Inc., Butler,

PA)

1300°C in air using five different specimenslloading

configurations, including pure tension, pure

compression, four-point uniaxial flexure, ball-on-ring

biaxial flexure, and ring-on-ring biaxial flexure. The

test specimenlloading configurations used in creep

testing are depicted in Figure

Detailed experimental

procedures and techniques can be found elsewhere

[9].

Briefly, in pure tension, the dog-bone-shaped, pin-

loaded tension specimens with round cross-section