Хлопков Ю.И., Жаров В.А., Горелов С.Л. Лекции по теоретическим методам исследования турбулентности

Подождите немного. Документ загружается.

(156)

где интеграл от S по области 0 ≤ k, j ≤ k′ исчезает (см., например, уравнение (131)). После этого

влияние нелинейного члена в рассмотренном выше уравнении можно проинтерпретировать как

перетекание энергии от мод

k ≤ k′ за счет инерциальной передачи к волновым числам k ≥ k′. В

соответствии с этим, если мы хотим смоделировать процесс перетекания энергии по аналогии с

вязкой диссипацией, введем эффективную турбулентную вязкость с помощью предположения о

том, что передача энергии может быть записана следующим образом:

(,) 2н(,) (,)

Tktdk k t Ektkdk

′′

′

=−

∫∫

, (157)

где

ν(k′, t) – кинематическая вихревая вязкость, которая представляет результат интегрирования по

волновым числам от

k′ до бесконечности. Это значит, что мы ищем выражение для вихревой

вязкости, которое содержит такой интеграл. Поэтому напишем

(,) [, (,)]

kt f jEjtdj

∞

′

∫

, (158)

где неизвестная функция может быть определена с помощью анализа размерности

3/2 1/2

[, (,)] [ (,)]

−

, (159)

где

A = const. Следовательно, вихревая вязкость по Гейзенбергу определяется выражением

3/2 1/2

н(,) [(,)]

kt Aj Ejt dj

∞

−

′

∫

. (160)

Эти уравнения были решены только для стационарного случая (см. [Бэтчелор, 1971]). Отметим

только что результирующий спектр сводится к колмогоровскому закону «–5/3» в инерциальной

области волновых чисел, но ведет себя как

–7

в диссипативной области. Как известно, этот

последний закон поведения неправилен, так как экспериментальные результаты показывают, что

энергетический спектр при больших волновых числах спадает экспоненциально, т. е. быстрее

любой степени.

Рассмотрим снова уравнение (121) для энергетического спектра, но на этот раз будем

интересоваться детальной структурой правой части уравнения и иерархией моментов, которая (в

принципе) определяет

T(k, t). Из уравнения (122) мы видим, что T(k, t) может быть выражена через

тройную корреляцию, которая в свою очередь может быть определена из уравнения (120) через

момент четвертого порядка. То есть если мы коротко запишем правую часть (120) в виде

бсу

/) (,, ;)LH tklp

, (161)

то формально можно записать решение уравнения (120) в виде

бсу

22 2

бсу

(,, ;)

exp н()()(,,

ds k l p t s H s

−∞

⎡⎤

=−++−

⎣⎦

∫

klp

;)

(162)

На этом этапе мы вводим гипотезу о квазинормальности [Прудман и Рид, 1954], [Тацуми, 1957],

которая утверждает, что все моменты четного порядка связаны так же, как и для нормального

распределения.

Заметим, что предположение о квазинорамальности значительно более слабое

утверждение, чем утверждение о нормальности поля скорости, которое нефизично, поскольку не

согласуется с существованием тройной корреляции, которая, как мы видели, ответственна за

передачу турбулентной энергии. Напротив, предположение о квазинормальности очень хорошо

подтверждается экспериментально [Френкель, Клебанов, 1967], [Ван Атта, Чен, 1969], [Ван Атта,

Чен, 1970], [Френкель, Клебанов, 1973], так как наблюдается именно эта связь между

корреляциями четного порядка, если пренебречь небольшим разбросом измеряемых результатов.

Гипотеза квазинормальности использована для замыкания иерархии уравнений, так как

позволяет выразить моменты четвертого порядка в правой части уравнения (120) через

произведение моментов второго порядка. Если мы обозначим момент четвертого порядка через

〈 1, 2, 3, 4〉 , то для нормального распределения получим

1,2,3,41,23,41,32,41,42,3=++

Применение этого соотношения к каждому из моментов четвертого порядка в правой части

уравнения (120) приводит к появлению девяти таких произведений моментов второго порядка –

степень алгебраической сложности, которая может показаться слишком большой. Однако на

практике, наоборот, это обстоятельство не является таким уж плохим, как может показаться на

первый взгляд. Не трудно видеть, что три таких члена обращаются тождественно в ноль. А из

шести оставшихся два члена можно объединить в один, как в конечном счете и четыре других,

оставляя только два члена в конце вычислений. Начать можно с первого члена в правой части

(120):

бсу

бвг в г с у

(2р /) (,,;)

() (,) ( ,) (,) (,)

{;бс}{ ;бу}

LH t

M u tu tu tu t

=−

+↔ ↔+ ↔ ↔

∑

klp

kjkjlp

kl kp

(163)

Если мы факторизуем квадрупольный момент в соответствии с нашими гипотезами, то получим

вг су

вс г у

ву г с

(,) ( ,) (,) (,)

(, ) ( , ) (, ) ( , )

(, ) (, ) ( , ) ( , )

(,) (,) ( ,) (,)

utu tutu t

ututu tu t

utu tu tut

−=

=−

+−

jkjl p

jkj lp

jl kjp

jp kjl

(164)

Теперь воспользуемся условием однородности для моментов второго порядка (см. соотношение

(98)):

• • В первом произведении из условия однородности j – k – j = 0 следует k = 0. Но

αβγ

(k) = 0 для k = 0, поэтому этот член равен нулю.

• • Во втором произведении условие однородности имеет вид k + l + p = 0.

• • В третьем k + l + p = 0.

Следовательно, суммируя по j (т. е. заменяя j на –l во втором произведении и на –p в третьем),

пользуясь соотношением (100) для тензора парных корреляций и условием симметрии оператора

инерционной передачи относительно перестановки последних двух индексов, мы преобразуем

предыдущее выражение первого члена в правой части уравнения (163) к виду

бвг вс гу

2(2

/) () () ()LM Q Qklp

Можно применить тот же метод к другим моментам четвертого порядка, при этом из (163)

получим

бсу бвг вс гу

(,, ;) () () ()

{;бс}{ ;бу}

HtMQQ=+

+↔ ↔+ ↔ ↔

klp k l p

kl kp

(165)

Теперь можно получить замкнутую форму для

T(k, t). Однако сначала мы заметим,

вспоминая (122), что нам нужно знать

βγα

(j, k – j, –k, t) и, следовательно, H

βγα

(j, k – j, –k, t). Делая

перестановки, аналогичные (165), получим

бсу бвг св уг

(,, ;) () () ( )

{;бв}{ ;бг}

HtMQQ=−

+− ↔ ↔ + ↔ − ↔

klp k +

kj kkj

(166)

На этой стадии ограничимся изотропным случаем, т. е. воспользуемся уравнением (102) для того,

чтобы выразить спектральный тензор через операторы проектирования и скалярную спектральную

плотность

Q(k, t). В соответствии с этим, выражая рассмотренное выше соотношение в

изотропном виде и подставляя в (122), можно

T(k, t) переписать в виде

{

}

22 2

бвг бсу св уг

(,) expн(||)(

4р [2 ( ) ( ) ( ) ( )

{;бв}{ ;бг}]

Tkt d ds k j k j t s

kM M D D

−∞

=++−

×−−

+− ↔ ↔ + ↔ − ↔

∫∫

kkjkj

kj kkj

)−×

(167)

Это выражение можно упростить еще, замечая, что при интегрировании по j переменная k – j

может быть заменена на j. Так в последнем члене уравнения (167) мы можем заменить k – j на j.

Алгебраические подробности можно найти в [МакКомб, 1990], где показано, что (167)

сравнительно просто приводится к

{}

[]

2222

(,)

exp н(||)(

2(,) (| |,) (,) (,)

Tkt

kd ds k j kj ts

LQ sQjsQks

−∞

=++−

×− −

∫∫

kj k j

)−×

(168)

где

бвг бсу св уг

свг всу уг

22 2 2

(,)

() ( ) () ( )

2()()()

[м()(12м ](1 м )

2 м

MM DD

MMD

k j kj kj

kj kj

=− − − =

=−

+−+ −

+−

kkjkj

kjkj

(169)

μ – косинус угла между векторами k и j. Формально уравнение (121) дает замкнутое уравнение

для энергетического спектра, если в него подставить выражение (168) для

T(k, t). Однако для того

чтобы быть последовательными и подтвердить то, что получается обычно на практике, мы будем

работать в терминах спектральной плотности

Q(k, t). Поэтому подставим (168) в (121), разделим

обе стороны на 4

πk

и, используя обобщение уравнения (107) для введения спектральной

плотности в левой части уравнения, получим замкнутое приближение, основанное на гипотезе

квазинормальности:

[]

22 2

[/ 2н ](,)

2expн(||)(

(,) (| |,) (,) (,)

ddt k Qkt

dds kjkjts

LQ sQjsQks

−∞

⎡⎤

=−++−

⎣⎦

×− −

∫∫

kj k j

)−×

(170)

Если положить, что

Q(k, t) задано при t = 0, уравнение (170) можно проинтегрировать по

времени для случая свободно затухающей турбулентности. К сожалению, вопреки очевидной

обоснованности природы основных предположений, при численном решении (170) ([О’Брайен,

Френсис, 1962], [Огура, 1963], критический обзор [Орзаг, 1970]) было получено, что

Q(k, t)

становится отрицательной при некоторых значениях волнового числа

k. Конечно, не видно

причин, почему бы приближенной теории не нарушать в некоторой малой степени применимость

начальных предположений. Но проблема квазинормальности состоит в том, что полученный

эффект не является малым.

Это рассмотрение квазинормальности представляет не только исторический интерес. При

выводе уравнения (170) мы воспользовались алгебраическими выкладками, которые многие

исследователи считают слишком пугающими, при столкновении с современными

аппроксимациями в проблеме замыкания. Таким образом, результат будет полезным в

дальнейшем изложении.

Ранее мы ввели одномерный спектр

), который определен на интервале –∞ ≤ k

≤ ∞ и

связан со среднеквадратичной скоростью соотношением (112). На практике экспериментатор

часто использует функцию

Φ(k

), которая определена на интервале 0≤ k

≤ ∞ и удовлетворяет

условию

11 1

()kdk u

∞

Φ=

∫

. (171)

Очевидно, что Φ(k

) равна удвоенной E

), но ради простоты будем следовать практике

экспериментаторов при представлении результатов.

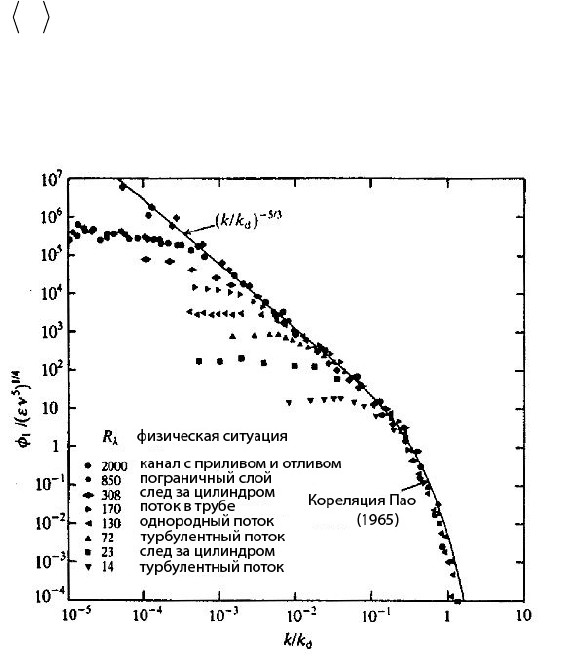
Рис. 7. Измеренные одномерные спектры для широкого диапазона

чисел Рейнольдса и физических ситуаций: ▼ – Стюарт и Таунсенд (1951), ■ – Уберой и Фреймут (1969), ▲–

Комте-Беллот и Коррзин (1971), ◄ – Чампэйн, Харрис, Коррзин (1970), ► – Лауфер (1954),

Ò – Уберой и Фреймут (1969), ● – Коантиц и Фавр (1974),

Ü – Грант и др. (1962)

На рис. 7 представлены экспериментальные данные для Φ(k

), полученные из многих

отличающихся друг от друга экспериментальных ситуаций: от лабораторных исследований в

аэродинамических трубах до классических морских исследований Гранта и др. (1962)

в каналах с

приливом и отливом. Поскольку физические источники данных столь различны (а мы

интересовались только мелкомасштабной структурой), то каждая совокупность данных

характеризовалась числом Рейнольдса R

, определяемого по микромасштабу Тейлора:

R л / нu=

, (172)

где

u – среднеквадратичная скорость, ν – кинематическая вязкость, а микромасштаб Тейлора

определен соотношением (79). Можно видеть, что спектры построены в переменных Колмогорова,

определенных формулами (146) и (147) и построены относительно безразмерной переменной

k/k

Ясно, что спектры при больших волновых числах сходятся к универсальной кривой,

подтверждая тем самым первую гипотезу Колмогорова о подобии, которая подытожена

соотношением (149). С ростом числа Рейнольдса также видно, что спектры демонстрируют

увеличение области (по волновым числам) универсального поведения с тенденцией

асимптотического отхода от закона

–5/3

(предсказанного во второй гипотезе подобия

Колмогорова: см. (149)) при малых волновых числах. Таким же образом можно отметить, что

постоянная асимптота каждого спектра при малых волновых числах – это в чистом виде артефакт,

возникающий как следствие одномерности спектра, который является неполным отображением

трехмерного спектра. С точки зрения физики это означает, что часть

Φ(k

), относящаяся к малым

k, подвержена сильному влиянию выравнивания от больших волновых чисел, движущихся под

углом к оси

(см. [Теннекес, Ламли, 1972]).

Константа пропорциональности

α в спектре Колмогорова долгое время была целью

теоретических предсказаний, поэтому ее экспериментальная величина так важна. Для начала

заметим [Бэтчелор, 1971], что из колмогоровского спектра следует

5/3

2/3

11 1 1

() бе

Ek k

−

. (173)

Требуя, чтобы

Φ(k

) равнялось удвоенному E

), убеждаемся, что измерение спектральной

функции

5/3

2/3

111

() беkk

−

Φ=

(174)

показывает, что константа (151) определяется соотношением

бб

. (175)

Результаты Гранта и др. (1962), которые можно рассматривать как наиболее надежные,

дают

= 0,47 ± 0,02. Следовательно, α = 1,44 ± 0,06. Другие исследования дают несколько

отличный результат, но все исследователи в этой области утверждают, что величина этой

постоянной находится вблизи 1.5.

Однако это согласие не является единодушным. Кречнан (1966) показал, что постоянная

зависит о того, где выбирается граница между инерционной и диссипативной областями. Обычно

она определяется соотношением

k = 0,1 k

, но, как видно на рис. 7, это иногда трудно сделать

достаточно аккуратно. Очевидно, мы можем сделать это с аналитическим видом, который можно

хорошо подобрать в обеих областях волновых чисел. Были предложены различные модели и связи

для достижения этой цели. Вероятно, наиболее известная из них – это аппроксимация Пао (1965).

Существенно, что аргументы Пао заключались в том, что скорость, с которой энергия

передается в пространстве волновых чисел, имеет ту же зависимость от вязкости, что и

энергетический спектр. Так отношение этих двух величин не зависит от вязкости: это верно в

инерционной области (в колмогоровском представлении) и, следовательно, в этой области

получается закон Колмогорова «–5/3». Если эту гипотезу распространить на область диссипации,

то получим, что выражение (154) перейдет в

{

}

2/3 5/3 4/3

() бе exp (3/ 2)( / )

Ek k k k

−

=−

, (176)

которое, как показывает рис. 7, очень хорошо согласуется с экспериментом. Это основное

предположение в работе Пао оказалось совершенно не оценено и не представлено здесь в качестве

спектральной теории (хотя были сделаны попытки ее усовершенствовать [Пао, 1968], [Теннекес,

1968], [Лин, 1972] или распространить ее на малые волновые числа [Дрискол, Кеннеди, 1983]).

Существенно, что это оказался хороший путь анализа экспериментальных результатов. А с нашей

точки зрения наиболее заслуживает внимания в этом анализе способ, с помощью которого он

привлекает внимание к тому факту, что величина

α, большая 2,2 (или возможно еще больше), не

совместима с данными: см., в частности, [Гибсон и др., 1970].

4. Перенормировочная теория возмущений

В этом пункте мы будем обращаться с проблемой замыкания моментов в теории

турбулентности очень специфично. Начнем с общего формализма, часто называемого «лямбда-

разложением», а затем продолжим рассмотрение конкретных теорий. Эти теории разделены на два

класса. Сначала рассмотрим теории, которые несовместимы с колмогоровским распределением

энергии по волновым числам, а затем те, которые совместимы.

Начать можно с того, что методы, которые мы обсуждаем, впервые появились в теории

многих тел статистической физики. Для того чтобы дать представление об общем методе,

рассмотрим случай реального газа, который лишь слегка неидеален. Очевидно, существует

искушение представить это как возмущение идеального газа, в котором составляющие его

частицы не взаимодействуют друг с другом. В микроскопической физике основной величиной,

позволяющей нам вычислить статистическую сумму, является гамильтониан. Из статистической

суммы находятся макроскопические свойства системы. Для идеального газа гамильтониан может

быть записан как в виде суммы гамильтонианов отдельных частиц, т. е.

ideal i

∑

, (177)

где

– гамильтониан отдельной частицы, а суммирование проводится по N частицам,

составляющим систему.

Теперь предположим, что реальный газ имеет гамильтониан, который может быть записан

в виде

real i i j

iij

∑∑

, (178)

где первый член есть сумма индивидуальных кинетических энергий частиц, а второй – потенциал

двухчастичного взаимодействия (кулоновский или леннард-джонсоновский). В этом случае общая

стратегия в теории многих тел состоит в попытке заменить взаимодействующие частицы на

представительные квазичастицы, которые уже не взаимодействуют и могут быть описаны

одночастичными гамильтонианами:

real i

′

∑

(179)

Проблема теперь состоит в том, чтобы определить квазичастицы, для чего существует

много эвристических методов, каждый из которых приспособлен к конкретной физической

проблеме. Например, в случае колебаний решетки можно заметить, что переход от функции (178)

к функции (179) равносилен диагонализации гамильтониана, в соответствии с чем удобно

работать в терминах нормальных мод. Однако в общем случае существует только один метод,

который является развитием теории возмущений и иногда называется

λ-разложением.

Перепишем уравнение для гамильтониана реального газа, введя параметр

λ:

real i i j

iij

∑∑

(180)

с целью отметить порядок членов в разложении, который полагается равным 1 в конце

вычислений. Другими словами,

λ играет роль параметра разложения в теории возмущений. Но

поскольку он не мал, он не является критерием для обрыва ряда в каком-то конкретном порядке.

Тем не менее, продолжая этот пример из микроскопической физики, следующий шаг – это

выражение для конфигурационной части статистической суммы

exp л()

ZV d kT H

−−

⎛⎞

=−

⎜⎟

⎝⎠

∑

∫

. (181)

Экспонента разлагается в ряд по степеням

λ, которая полагается в конце вычислений равной

единице. Практическая трудность вычисления коэффициентов разложения связана с природой

потенциала взаимодействия. Но общая стратегия состоит в том, чтобы изучить и

классифицировать члены в каждом порядке – часто с помощью графиков или диаграмм для

упрощения выявления топологических свойств – и найти способ суммирования членов некоторого

вида во всех порядках по

λ. Получение таких частичных сумм часто сопровождается введением

эффективных масс или эффективных зарядов. Подобные подходы могут быть использованы и в

турбулентности, но здесь перенормированная величина – это эффективная вязкость.

Турбулентность не является гамильтоновой системой, хотя можно сформулировать задачу

с помощью лиувиллиана, чтобы подчеркнуть сходство с микроскопическими теориями,

рассмотренными выше. Однако обычно работают непосредственно с уравнениями Навье–Стокса,

с моментами поля скорости, что мы и будем делать далее.

Рассмотрим уравнения Навье–Стокса в форме (134), но теперь введем параметр

λ в

нелинейный член

бвг в г б

н (,)

л () (,) ( ,) (,).

ku t

utu tf t

∂

⎛⎞

⎜⎟

⎝⎠

=−

∑

kjkj k

(182)

Мы напоминаем, что параметр

λ равен единице и используется только для упорядочения членов

разложения. Сам по себе этот параметр не может быть использован для оправдания обрывания

ряда. В соответствии с этим (182) в точности совпадает уравнением (134).

Это уравнение содержит силу, которая определена так же, как и ранее. Мы требуем, чтобы

взбалтывающая сила удовлетворяла условию (135) и имела гауссовское распределение

вероятности, автокорреляция которого задается соотношением (137). Во всем остальном она

произвольна. Формулировка проблемы турбулентности основана на предположении о том, что

нелинейное взаимодействие, индуцированное уравнением (182), будет приводить к

универсальному турбулентному полю скорости независимо от природы взбалтывающей силы.

Однако существо проблемы турбулентности в том, что результирующее поле скорости при этом

оказывается заметно негауссовским.

Это обстоятельство создает сложности в теории турбулентности. Для того чтобы решить

проблему замыкания, нужно получить соотношения между моментами разных порядков. Но, к

сожалению, это можно сделать только для нормального (гауссовского) распределения. Мы уже

видели, что гипотеза квазинормальности, которая предполагает связь между моментами

четвертого и второго порядков, не работает. Очевидно, надо соблюдать осторожность

относительно способа, с помощью которого турбулентное поле можно рассматривать как

возмущение нормального процесса. Конкретный путь реализации этих представлений отличает

одну теорию турбулентности от другой. Можно обеспечить условия, в которых легко обсуждать

различные подходы, если изложить сначала некоторый общий формализм. Мы сделаем это

следующим образом.

Рассмотрим уравнения Навье–Стокса при

λ = 0, т. е. мы проводим мысленный

эксперимент, в котором жидкость приводится в движение взбалтывающей силой, но нелинейные

члены отключены. В этих условиях отклик жидкости определяется кинематической вязкостью, так

что решение (182) можно записать в виде

(0) 2

б 0 б

( , ) exp{ н ()}(,

utdt kttf

−∞

′′

=−−

∫

, (183)

где верхний индекс «0» указывает на то, что поле скорости является решением уравнений Навье–

Стокса при

λ = 0.

Желая свести математические сложности к минимуму, рассмотрим основную идею,

которая заключается во введении очень простой формы записи. Представим (183) в виде

() ()00

= f

, (184)

где G

(0)

– функция Грина exp{–ν

(t – t′)}. Здесь и далее мы будем использовать целые числа для

того, чтобы отличать поля.

Из последнего уравнения, а также из определения взбалтывающей силы следует, что поле

(0)

имеет нормальное распределение, поэтому его моменты удовлетворяют ряду соотношений. Во-

первых, все нечетные моменты равны нулю:

(0) (0) (0)

(1) (2)... ( ) 0, 2 1uu un nm==+

. (185)

Теперь если скомбинировать свойство однородности с факторизацией гауссовских моментов

четного порядка, то получим

(0) (0) (0)

(1) ( 2) д (1)uu Q=

, (186)

(0) (0) (0) (0)

(0) (0)

12 34

(0)(0) (0)(0)

13 24 14 23

(1)(2)(3)(4)

дд (1) (3)

дд (1) (2) дд (1) (2),

uu u u

QQ QQ

(187)

где целые числа 1, 2, ...,

n соответствуют волновым числам k

, k

, …, k

, а Q

(0)

– очевидное

обобщение записи момента второго порядка (или спектральной плотности) для поля нулевого

приближения.

Мы можем завершить наш мысленный эксперимент включением нелинейных членов,

скажем при

t = –∞. Влияние нелинейных членов выражается, благодаря нелинейному

перемешиванию, в том, что все моды нулевого приближения оказываются связанными в

результирующем поле

u(k). И, конечно же, u(k) сильно отличается от гауссовского распределения.

Можно выразить это математически, выписав выражение для результирующего поля с

помощью ряда теории возмущений:

(0) (1) 2 (2)

() () л () л () ...uk u k u k u k=+ + +

(188)

В этом разложении только результирующее поле и поле нулевого приближения имеют ясный

физический смысл. Другие члены

(1)

, u

(2)

, … являются членами высшего порядка и могут быть

выражены итеративно с помощью поля нулевого приближения. Они могут быть вычислены

подстановкой выражения (188) в уравнение (182) и приравниванием членов одного порядка по

λ.

В результате:

(1) (0) (0) (0)

,uGMuu=

(189)

(2) (0) (0) (0) (0) (0)

2uGMuGMuu=

(190)

(3) (0) (0) (0) (0) (0) (0) (0)

(0) (0) (0) (0) (0) (0) (0)

u G Mu G Mu G Mu u

GMGMuuGMuu

(191)

и так далее.

Если подставить эти члены обратно в уравнение (188), то можно проинтерпретировать

разложение на основе порядка сложности связи мод. С точки зрения наших предварительных

замечаний относительно проблем описания на микроуровне систем типа неидеального газа

интересно отметить, что имеется сходство между написанным выше разложением и, скажем,

кластерным вириальным разложением. Однако, с нашей точки зрения, уравнение (188) с учетом

(189) – (191) и остальных порядков дает общее выражение для точного (негауссового) поля

скорости с помощью гауссового поля нулевого приближения.

Можно подчеркнуть этот аспект, записывая выражение для моментов второго порядка. В

нашей скелетной системе записи

Q(k) = 〈 u(k) u(–k)〉 , поэтому, подставляя выражения из

предыдущего уравнения и выполняя усреднение, получим

(0) (0) (0) (0) 4

() (л )QkQGMMQQO=+ +

. (192)

Это наша общая форма для точных моментов второго порядка (спектральной плотности),

выраженных чрез моменты нулевого приближения. Если бы

λ было малым, то можно было бы

оборвать правую часть (192) на некоторых подходящих членах, как делается в обычной теории

возмущений. Однако на некоторой стадии следует положить

λ = 1, и в этих условиях может не

быть оправдания для обрывания ряда на членах низкого порядка. Если мы и знаем что-либо об

этом ряде, так это то, что он в высшей степени расходящийся. В следующем пункте рассмотрим

способ, с помощью которого может быть достигнута перенормировка.

В этом пункте техника перегруппировки и частичного суммирования, используемые в

λ-

разложении в микроскопической физике, применена к ряду теории возмущений в уравнениях

Навье–Стокса. Впервые это было сделано Уайлдом (1961), который предложил анализ скалярного

аналога этих уравнений, который позже был обобщен Ли (1965) на трехмерные уравнения Навье–

Стокса, а также на уравнения магнитной гидродинамики. Дадим здесь лишь некоторое

представление об этой технике, полное описание которой наряду с обоснованием некоторых

аспектов можно найти в различных изданиях [МакКомб, 1990]. Однако краткое изложение

предпочтительно, по сравнению с длинным перечислением ограничений, если мы хотим увидеть,

как возникают перенормированные величины в самом общем виде.

Начнем со смены терминологии. Будем называть

(0)

и G

(0)

корреляцией и пропагатором в

нулевом порядке соответственно. Оправдание названия последней величины связано с тем, что

функция Грина дает зависимость от времени для поля скорости в отсутствие нелинейных

эффектов, а также отклик на внешнюю силу в соответствии с уравнением (183). Очевидно, мы

хотим определить точные (перенормированные) корреляцию и пропагатор. Способ, которым это

будет сделано, принадлежит больше к топологии, чем к физике.

Если мы рассмотрим ряд теории возмущений для поля скорости (188) с учетом

соотношений (189) – (191), то, как мы уже замечали, он может быть интерпретирован с точки

зрения разложения по сложности членов. Очевидно, что это – топологическое свойство, поэтому

введем диаграммное представление разложения для прояснения топологического аспекта.

Сделаем это, если установим соответствие между математическим выражением членов и

элементами диаграмм следующим образом:

сплошная линия

↔u

(0)

пунктирная линия

↔G

(0)

(193)

точка (вершина)

↔M .

Используя эти обозначения, можно записать ряд теории возмущений (188) в диаграммной

форме, как показано на рис. 8.