Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

So far, all of the examples of comparative statics that we have considered have been taken

from macroeconomics. The same approach can be used in microeconomics. For example, let

us analyse the equilibrium price and quantity in supply and demand theory.

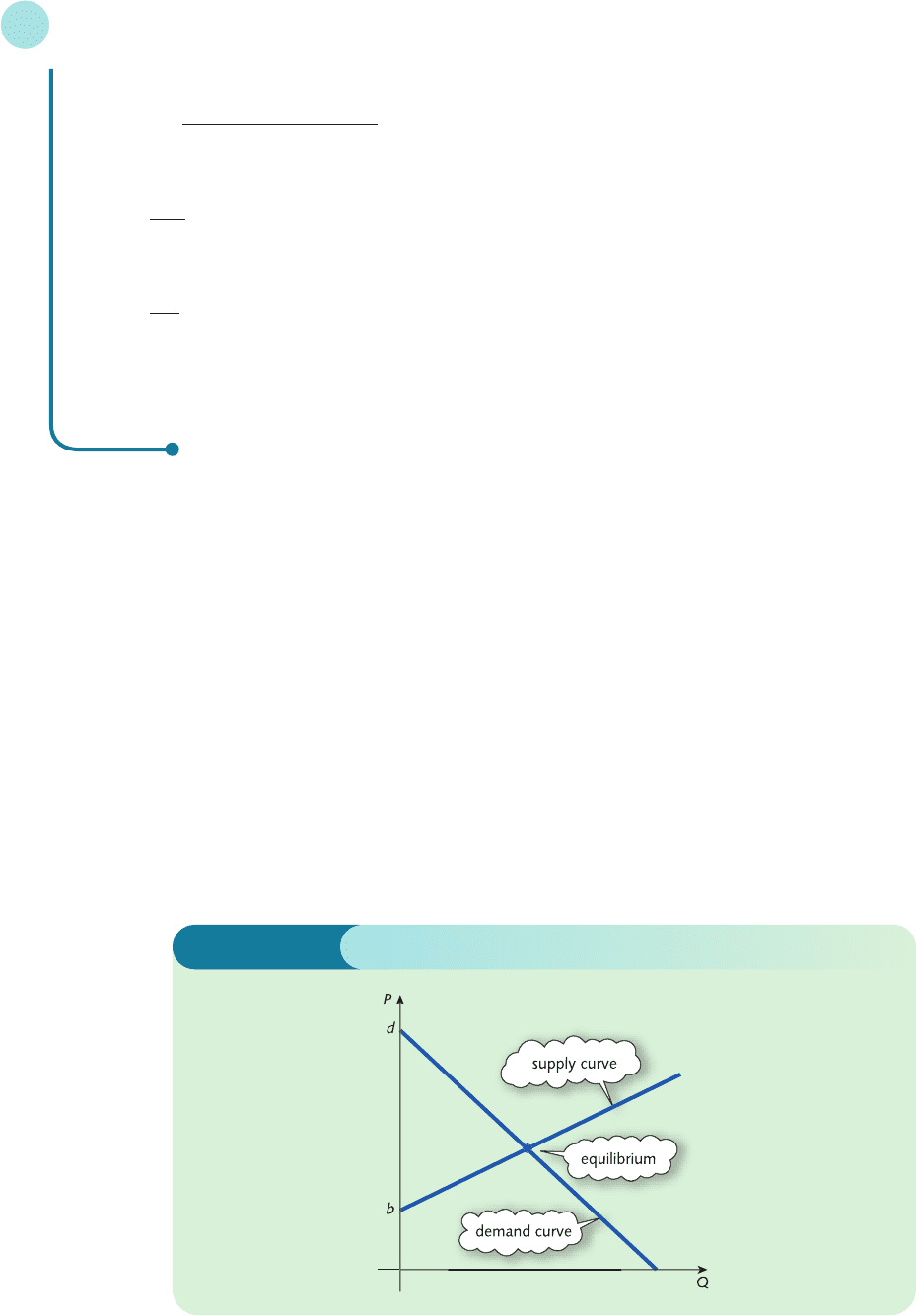
Figure 5.10 illustrates the simple linear one-commodity market model described in Section

1.3. The equilibrium values of price and quantity are determined from the point of intersection

of the supply and demand curves. The supply curve is a straight line with a positive slope and

intercept, so its equation may be written as

P = aQ

+ b (a > 0, b > 0)

The demand equation is also linear but has a negative slope and a positive intercept, so its equa-

tion may be written as

P =−cQ

+ d (c > 0, d > 0)

It is apparent from Figure 5.10 that in order for these two lines to intersect in the positive quad-

rant, it is necessary for the intercept on the demand curve to lie above that on the supply curve,

so we require

Partial Differentiation

380

Figure 5.10

(a) Show that

Y =

(b) Write down the autonomous export multiplier

and the marginal propensity to import multiplier

Deduce the direction of change in Y due to increases in X* and m.

level of national income, Y, and the change in Y due to a 10 unit increase in autonomous exports.

∂Y

∂m

∂Y

∂X*

b + I* + G* + X* − M*

1 − a + m

MFE_C05c.qxd 16/12/2005 10:41 Page 380

d > b

or equivalently

d − b > 0

In equilibrium Q

and Q

are equal. If we let their common value be denoted by Q then the

supply and demand equations become

P = aQ + b

P =−cQ + d

and so

aQ + b =−cQ + d

since both sides are equal to P.

To solve for Q we ﬁrst collect like terms together, which gives

(a + c)Q = d − b

and then divide by the coefﬁcient of Q to get

Q =

(Incidentally, this conﬁrms the restriction d − b > 0. If this were not true then Q would be either

zero or negative, which does not make economic sense.)

Equilibrium quantity is a function of the four parameters a, b, c and d, so there are four

multipliers

=−

where the chain rule is used to ﬁnd ∂Q/∂a and ∂Q/∂c.

We noted previously that all of the parameters are positive and that d − b > 0, so

< 0, < 0, < 0 and > 0

This shows that an increase in a, b or c causes a decrease in Q, whereas an increase in d causes

an increase in Q.

∂Q

∂d

∂Q

∂c

∂Q

∂b

∂Q

∂a

a + c

∂Q

∂d

d − b

(a + c)

∂Q

∂c

a + c

∂Q

∂b

d − b

(a + c)

∂Q

∂a

d − b

a + c

5.3 • Comparative statics

381

Example

Give a graphical conﬁrmation of the sign of the multiplier

∂Q

∂a



MFE_C05c.qxd 16/12/2005 10:41 Page 381

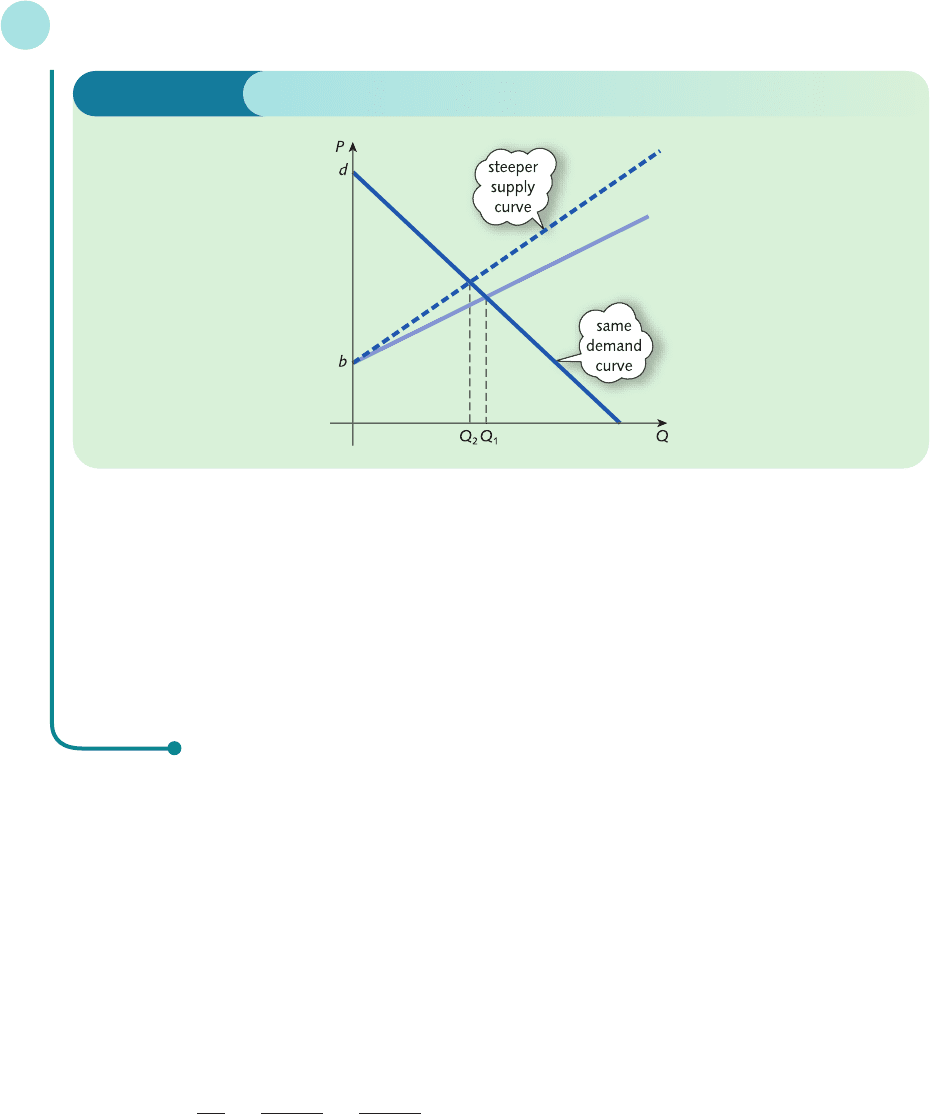
Solution

From the supply equation

P = aQ

+ b

we see that a small increase in the value of the parameter a causes the supply curve to become slightly

steeper, as indicated by the dashed line in Figure 5.11. The effect is to shift the point of intersection to the

left and so the equilibrium quantity decreases from Q

to Q

which is consistent with a negative value of the

multiplier, ∂Q/∂a.

Partial Differentiation

382

Figure 5.11

Given any pair of supply and demand equations, we can easily calculate the effect on the

equilibrium quantity. For example, consider the equations

P = Q

+ 1

P =−2Q

+ 5

and let us suppose that we need to calculate the change in equilibrium quantity when the

coefﬁcient of Q

increases from 1 to 1.1. In this case we have

a = 1, b = 1, c = 2, d = 5

To ﬁnd ∆Q we ﬁrst evaluate the multiplier

=− =− =−0.44

and then multiply by 0.1 to get

∆Q = (−0.44) × 0.1 =−0.044

An increase of 0.1 in the slope of the supply curve therefore produces a decrease of 0.044 in the

equilibrium quantity.

5 − 1

(1 + 2)

d − b

(a + c)

∂Q

∂a

MFE_C05c.qxd 16/12/2005 10:41 Page 382

Throughout this section all of the relations in each model have been assumed to be linear. It

is possible to analyse non-linear relations in a similar way, although this is beyond the scope of

this book.

5.3 • Comparative statics

383

Practice Problem

3 Give a graphical confirmation of the sign of the multiplier

for the linear one-commodity market model

P = aQ

+ b (a > 0, b > 0)

P =−cQ

+ d (c > 0, d > 0)

∂Q

∂d

Advice

We shall return to this topic again in Chapter 7 when we use Cramer’s rule to solve the

structural equations of a linear model.

Autonomous consumption multiplier The number by which you multiply the change in

autonomous consumption to deduce the corresponding change in, say, national income:

∂Y/∂b.

Balanced budget multiplier The number by which you multiply the change in govern-

ment expenditure to deduce the corresponding change in, say, national income: ∂Y/∂G*,

assuming that this change is ﬁnanced entirely by a change in taxation.

Comparative statics Examination of the effect on equilibrium values due to changes in the

parameters of an economic model.

Dynamics Analysis of how equilibrium values vary over time.

Investment multiplier The number by which you multiply the change in investment to

deduce the corresponding change in, say, national income: ∂Y/∂I*.

Marginal propensity to consume multiplier The number by which you multiply the

change in MPC to deduce the corresponding change in, say, national income: ∂Y/∂a.

Reduced form The ﬁnal equation obtained when exogenous variables are eliminated in the

course of solving a set of structural equations in a macroeconomic model.

Statics The determination of the equilibrium values of variables in an economic model

which do not change over time.

Structural equations A collection of equations that describe the equilibrium conditions of

a macroeconomic model.

Key Terms

MFE_C05c.qxd 16/12/2005 10:41 Page 383

Partial Differentiation

384

Practice Problems

4 Consider the three-sector model

Y = C + I + G (1)

C = aY

+ b (0 < a < 1, b > 0) (2)

= Y − T (3)

T = T*(T* > 0) (4)

I = I*(I* > 0) (5)

G = G*(G* > 0) (6)

(a) Show that

C =

(b) Write down the investment multiplier for C. Decide the direction of change in C due to an increase

in I*.

also the change in C due to a 2 unit change in investment.

5 Consider the four-sector macroeconomic model

Y = C + I + G + X − M

C = aY

+ b (0 < a < 1, b > 0)

= Y − T

T = tY + T* (0 < t < 1, T * > 0)

I = I*(I* > 0)

G = G*(G* > 0)

X = X*(X* > 0)

M = mY

+ M* (0 < m < 1, M* > 0)

(1) Show that

Y =

(2) (a) Write down the autonomous taxation multiplier. Deduce that an increase in T* causes a

decrease in Y on the assumption that a country’s marginal propensity to import, m, is less than

its marginal propensity to consume, a.

(b) Write down the government expenditure multiplier. Deduce that an increase in G* causes an

increase in Y.

(3) Let a = 0.7, b = 150, t = 0.25, m = 0.1, T* = 100, I* = 100, G* = 500, M* = 300 and X* = 160.

(a) Calculate the equilibrium level of national income.

(b) Calculate the change in Y due to an 11 unit increase in G*.

b + (m − a)T* + I* + G* + X * − M*

1 − a + at + m − mt

aI* + aG* − aT * + b

1 − a

MFE_C05c.qxd 16/12/2005 10:41 Page 384

6 Show that the equilibrium price for a linear one-commodity market model

P = aQ

+ b (a > 0, b > 0)

P =−cQ

+ d (c > 0, d > 0)

where d − b > 0, is given by

P =

Find expressions for the multipliers

,,,

and deduce the direction of change in P due to an increase in a, b, c or d.

7 (1) For the commodity market

Y = C + I

C = aY + b (0 < a < 1, b > 0)

I = cr + d (c < 0, d > 0)

where r is the interest rate.

Show that, when the commodity market is in equilibrium,

(1 − a)Y − cr = b + d

(2) For the money market

(money supply) M

= M*

(M*

> 0)

(total demand for money) M

= k

Y + k

r + k

> 0, k

< 0, k

> 0)

(equilibrium) M

= M

Show that when the money market is in equilibrium

Y + k

r = M*

− k

(3) (a) By solving the simultaneous equations derived in parts (1) and (2) show that when the com-

modity and money markets are both in equilibrium

Y =

(b) Write down the money supply multiplier, ∂Y/∂M

* and deduce that an increase in M

* causes

an increase in Y.

(b + d) + c(M*

− k

)

(1 − a)k

+ ck

∂P

∂d

∂P

∂c

∂P

∂b

∂P

∂a

ad + bc

a + c

5.3 • Comparative statics

385

MFE_C05c.qxd 16/12/2005 10:41 Page 385

section 5.4

Unconstrained optimization

As you might expect, methods for ﬁnding the maximum and minimum points of a function of

two variables are similar to those used for functions of one variable. However, the nature of

economic functions of several variables forces us to subdivide optimization problems into

two types, unconstrained and constrained. To understand the distinction, consider the utility

function

U(x

, x

) = x

1/4

3/4

The value of U measures the satisfaction gained from buying x

items of a good G1 and x

items

of a good G2. The natural thing to do here is to try to pick x

and x

to make U as large as

possible, thereby maximizing utility. However, a moment’s thought should convince you that,

as it stands, this problem does not have a ﬁnite solution. The factor x

1/4

can be made as large as

we please by taking ever-increasing values of x

and likewise for the factor x

3/4

. In other words,

utility increases without bound as more and more items of goods G1 and G2 are bought.

In practice, of course, this does not occur, since there is a limit to the amount of money that

an individual has to spend on these goods. For example, suppose that the cost of each item of

G1 and G2 is $2 and $3, respectively, and that we allocate $100 for the purchase of these goods.

The total cost of buying x

items of G1 and x

items of G2 is

Objectives

At the end of this section you should be able to:

 Use the ﬁrst-order partial derivatives to ﬁnd the stationary points of a function

of two variables.

 Use the second-order partial derivatives to classify the stationary points of a

function of two variables.

 Find the maximum proﬁt of a ﬁrm that produces two goods.

 Find the maximum proﬁt of a ﬁrm that sells a single good in different markets

with price discrimination.

MFE_C05d.qxd 16/12/2005 10:42 Page 386

+ 3x

so we require

+ 3x

= 100

The problem now is to maximize the utility function

U = x

1/4

3/4

subject to the budgetary constraint

+ 3x

= 100

The constraint prevents us from taking ever-increasing values of x

and x

and leads to a ﬁnite

solution.

We describe how to solve constrained optimization problems in the following two sections.

For the moment we concentrate on the simple case of optimizing functions

z = f(x, y)

without any constraints. This is typiﬁed by the problem of proﬁt maximization, which usually

has a ﬁnite solution without the need to impose constraints. In a sense the constraints are built

into the proﬁt function, which is deﬁned by

π=TR − TC

because there is a conﬂict between trying to make total revenue, TR, as large as possible while

trying to make total cost, TC, as small as possible.

Let us begin by recalling how to ﬁnd and classify stationary points of functions of one variable

y = f(x)

In Section 4.6 we used the following strategy:

Step 1

Solve the equation

f ′(x) = 0

to ﬁnd the stationary points, x = a.

Step 2

 f ″(a) > 0 then the function has a minimum at x = a

 f ″(a) < 0 then the function has a maximum at x = a

 f ″(a) = 0 then the point cannot be classiﬁed using the available information

For functions of two variables

z = f(x, y)

the stationary points are found by solving the simultaneous equations

= 0

∂z

∂y

∂z

∂x

5.4 • Unconstrained optimization

387

MFE_C05d.qxd 16/12/2005 10:42 Page 387

that is,

(x, y) = 0

This is a natural extension of the one-variable case. We ﬁrst write down expressions for the

ﬁrst-order partial derivatives and then equate to zero. This represents a system of two equations

for the two unknowns x and y, which we hope can be solved. Stationary points obtained in this

way can be classiﬁed into one of three types: minimum, maximum and saddle point.

Figure 5.12(a) shows the shape of a surface in the neighbourhood of a minimum. It can be

thought of as the bottom of a bowl-shaped valley. If you stand at the minimum point and walk

in any direction then you are certain to start moving upwards. Mathematically, we can classify

a stationary point (a, b) as a minimum provided that all three of the following conditions hold:

> 0, > 0, −

> 0

when x = a and y = b: that is,

(a, b) > 0, f

(a, b) f

(a, b) − [ f

(a, b)]

> 0

This triple requirement is obviously more complicated than the single condition needed in the

case of a function of one variable. However, once the second-order partial derivatives have

been evaluated at the stationary point, the three conditions are easily checked.

Figure 5.12(b) shows the shape of a surface in the neighbourhood of a maximum. It can be

thought of as the summit of a mountain. If you stand at the maximum point and walk in any

direction then you are certain to start moving downwards. Mathematically, we can classify a

stationary point (a, b) as a maximum provided that all three of the following conditions hold:

< 0, < 0, −

> 0

when x = a and y = b: that is,

(a, b) < 0, f

(a, b) f

(a, b) − [ f

(a, b)]

> 0

Of course, any particular mountain range may well have lots of valleys and summits. Likewise,

a function of two variables can have more than one minimum or maximum.

Figure 5.12(c) shows the shape of a surface in the neighbourhood of a saddle point. As its

name suggests, it can be thought of as the middle of a horse’s saddle. If you sit at this point and

edge towards the head or tail then you start moving upwards. On the other hand, if you edge

sideways then you start moving downwards (and will probably fall off!). Mathematically,

we can classify a stationary point (a, b) as a saddle point provided that the following single

condition holds:

−

< 0

∂

∂x∂y

∂

∂y

∂

∂x

∂

∂x∂y

∂

∂y

∂

∂x

∂

∂y

∂

∂x

∂

∂x∂y

∂

∂y

∂

∂x

∂

∂y

∂

∂x

Partial Differentiation

388

Figure 5.12

MFE_C05d.qxd 16/12/2005 10:42 Page 388

when x = a and y = b: that is,

(a, b) f

(a, b) − [ f

(a, b)]

< 0

To summarize, the method for ﬁnding and classifying stationary points of a function f(x, y) is

as follows:

Step 1

Solve the simultaneous equations

(x, y) = 0

to ﬁnd the stationary points, (a, b).

Step 2

 f

> 0, f

> 0 and f

− f

> 0 at (a, b) then the function has a minimum at (a, b)

 f

< 0, f

< 0 and f

− f

> 0 at (a, b) then the function has a maximum at (a, b)

 f

− f

< 0 at (a, b) then the function has a saddle point at (a, b)

5.4 • Unconstrained optimization

389

Advice

The second-order conditions needed to classify a stationary point can be expressed more

succinctly using Hessians. Details are given in Appendix 3 at the end of this book, although

you will need to be familiar with determinants of 2 × 2 matrices, which are covered later

in Section 7.2.

Example

Find and classify the stationary points of the function

f(x, y) = x

− 3x + xy

Solution

In order to use steps 1 and 2 we need to ﬁnd all ﬁrst- and second-order partial derivatives of the function

f(x, y) = x

− 3x + xy

These are easily worked out as

= 3x

− 3 + y

= 2xy

= 6x

= 2y

= 2x



MFE_C05d.qxd 16/12/2005 10:42 Page 389