Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

Solution

We need to ﬁnd

which denotes the function obtained by differentiating ﬁrst with respect to x

and then with respect to x

Differentiating with respect to x

gives

==3x

+ x

and if we further differentiate this with respect to x

we get

==2x

In fact, as we have just noted for functions of two variables, we get the same answer if we differentiate in

reverse order. You might like to check this for yourself.

∂

∂x

∂f

∂x

∂

∂x

Partial Differentiation

350

Practice Problem

4 Find expressions for the partial derivatives f

, f

and f

in the case when

f(x

, x

) = x

+ x

− x

We have seen how to work out partial derivatives but have yet to give any meaning to them.

To provide an interpretation of a partial derivative, let us take one step back for a moment and

recall the corresponding situation for functions of one variable of the form

y = f(x)

The derivative, dy/dx, gives the rate of change of y with respect to x. In other words, if x changes

by a small amount ∆x then the corresponding change in y satisﬁes

∆y  ∆x

Moreover, the accuracy of the approximation improves as ∆x becomes smaller and smaller.

Advice

You might like to remind yourself of the reasoning behind this approximation, which was

explained graphically in Section 4.3.1.

Given the way in which a partial derivative is found, we can deduce that for a function of

two variables

z = f(x, y)

if x changes by a small amount ∆x and y is held ﬁxed then the corresponding change in z

satisﬁes

∆z  ∆x

∂z

∂x

MFE_C05a.qxd 16/12/2005 10:40 Page 350

Similarly, if y changes by ∆y and x is ﬁxed then z changes by

∆z  ∆y

In practice, of course, x and y may both change simultaneously. If this is the case then the net

change in z will be the sum of the individual changes brought about by changes in x and y

separately, so that

∆z  ∆x +∆y

This is referred to as the small increments formula. Although this is only an approximation,

it can be shown that for most functions the corresponding error tends to zero as ∆x and ∆y

both tend to zero. For this reason the formula is sometimes quoted with an equality sign and

written as

dz = dx +− dy

where the symbols dx, dy and dz are called differentials and represent limiting values of ∆x,

∆y and ∆z, respectively.

∂z

∂y

∂z

∂x

∂z

∂y

∂z

∂x

∂z

∂y

5.1 • Functions of several variables

351

Example

z = x

y − y

evaluate

and

at the point (1, 3). Hence estimate the change in z when x increases from 1 to 1.1 and y decreases from 3

to 2.8 simultaneously.

Solution

z = x

y − y

then

∂z/∂x = 3x

y − y

and ∂z/∂y = x

− 3y

so at the point (1, 3)

= 3(1)

(3) − 3

=−18

= 1

− 3(3)

(1) =−26

Now, since x increases from 1 to 1.1, the change in x is

∆x = 0.1

∂z

∂y

∂z

∂x

∂z

∂y

∂z

∂x



MFE_C05a.qxd 16/12/2005 10:40 Page 351

and, since y decreases from 3 to 2.8, the change in y is

∆y =−0.2

The small increments formula states that

∆z  ∆x +∆y

The change in z is therefore

∆z  (−18)(0.1) + (−26)(−0.2) = 3.4

so z increases by approximately 3.4.

∂z

∂y

∂z

∂x

Partial Differentiation

352

Practice Problem

5 If

z = xy − 5x + 2y

evaluate

and

at the point (2, 6).

(a) Use the small increments formula to estimate the change in z as x decreases from 2 to 1.9 and y

increases from 6 to 6.1.

(b) Confirm your estimate of part (a) by evaluating z at (2, 6) and (1.9, 6.1).

∂z

∂y

∂z

∂x

One important application of the small increments formula is to implicit differentiation. We

hope by now that you are entirely happy differentiating functions of one variable such as

y = x

+ 2x

+ 5

Suppose, however, that you are asked to ﬁnd dy/dx given the equation

+ 2xy

− x = 5

This is much more difﬁcult. The reason for the difference is that in the ﬁrst case y is given

explicitly in terms of x whereas in the second case the functional dependence of y on x is only

given implicitly. You would need to somehow rearrange this equation and to write y in terms

of x before you could differentiate it. Unfortunately, this is an impossible task because of the

presence of the y

term. The trick here is to regard the expression on the left-hand side of the

equation as a function of the two variables x and y, so that

f(x, y) = y

+ 2xy

− x

or equivalently

z = y

+ 2xy

− x

MFE_C05a.qxd 16/12/2005 10:40 Page 352

The equation

+ 2xy

− x = 5

then reads

z = 5

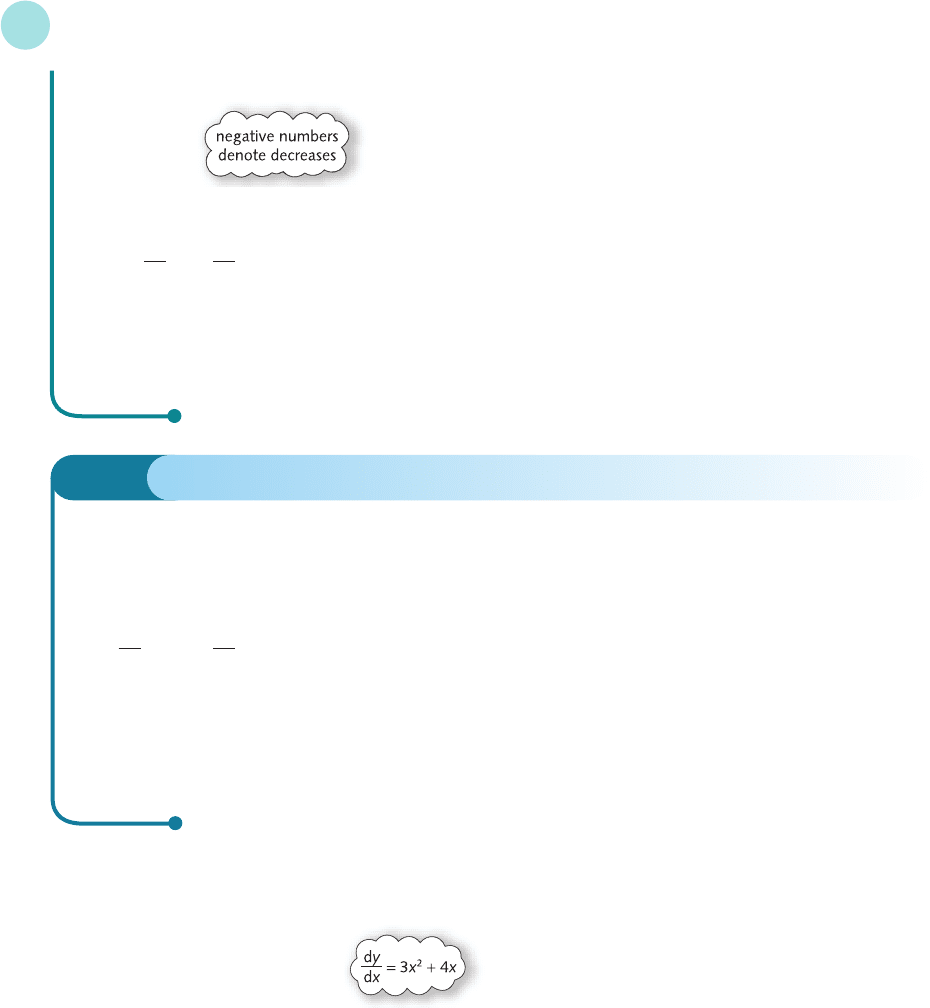
In general, the differential form of the small increments formula states that

dz = dx + dy

In our particular case, z takes the constant value of 5, so does not change. Hence dz = 0 and the

formula reduces to

0 = dx + dy

which rearranges as

dy =− dx

that is,

=−

This formula can be used to ﬁnd dy/dx given any implicit function

f(x, y) = constant

that is,

if f (x, y) = constant then =−

The technique of ﬁnding dy/dx from −f

is called implicit differentiation and can be used

whenever it is difﬁcult or impossible to obtain an explicit representation for y in terms of x.

∂z/∂x

∂z/∂y

∂z

∂x

∂z

∂y

∂z

∂y

∂z

∂x

∂z

∂y

∂z

∂x

5.1 • Functions of several variables

353

Example

Use implicit differentiation to ﬁnd an expression for dy/dx given that

+ 2xy

− x = 5

Solution

For the function

f(x, y) = y

+ 2xy

− x

we have

= 2y

− 1 and f

= 3y

+ 4xy

so that

=− =− =

−2y

+ 1

+ 4xy

− 1

+ 4xy

MFE_C05a.qxd 16/12/2005 10:40 Page 353

Partial Differentiation

354

Practice Problem

6 Use implicit differentiation to find expressions for dy/dx given that

(a)

xy − y

+ y = 0 (b) y

− xy

= 10

Advice

There is an alternative way of thinking about implicit differentiation which is based on the

chain rule and does not depend on partial differentiation at all. This is described in

Appendix 2. You might find it easier to use than the method described above.

Dependent variable A variable whose value is determined by that taken by the inde-

pendent variables; in z = f(x, y), the dependent variable is z.

Differentials Limiting values of incremental changes. In the limit, the approximation

∆z  ×∆x becomes dz  × dx where dz and dx are the differentials.

Function of two variables A rule that assigns to each pair of incoming numbers, x and y,

a uniquely deﬁned outgoing number, z.

Implicit differentiation The process of obtaining dy/dx where the function is not given

explicitly as an expression for y in terms of x.

Independent variable Variables whose values determine that of the dependent variable; in

z = f(x, y), the independent variables are x and y.

Partial derivative The derivative of a function of two or more variables with respect to

one of these variables, the others being regarded as constant.

Second-order partial derivative The partial derivative of a ﬁrst-order partial derivative.

For example, f

is the second-order partial derivative when f is differentiated ﬁrst with

respect to y and then with respect to x.

Small increments formula The result ∆z  ∆x +∆y

Symmetric function A function of two or more variables which is unchanged by any per-

mutation of the variables. A function of two variables is symmetric when f(x, y) = f(y, x)

∂z

∂y

∂z

∂x

∂z

∂x

∂z

∂x

Key Terms

Practice Problems

7 If

f(x, y) = 3x

evaluate f(2, 3), f(5, 1) and f(0, 7).

8 If

f(x, y) = 2xy + 3x

verify that f(5, 7) ≠ f(7, 5). Are there any pairs of numbers, (x, y) for which f(x, y) = f(y, x)?

MFE_C05a.qxd 16/12/2005 10:40 Page 354

9 Write down expressions for the first-order partial derivatives, and for

(a)

z = x

+ 4y

(b) z = 3x

− 2e

+ 5y

10 If

f(x, y) = x

− x

+ y

write down expressions for the first-order partial derivatives, f

and f

. Hence evaluate f

(1, 0) and

(1, 1).

11 Find expressions for all first- and second-order partial derivatives of the following functions. In each

case verify that

(a) z = xy (b) z = e

y (c) z = x

+ 2x + y (d) z = 16x

1/4

3/4

(e) z =+

12 Use the small increments formula to estimate the change in

z = x

− x

+ 4y

when

(a) x increases from 1 to 1.1 and y remains fixed at 0

(b) x remains fixed at 1 and y decreases from 0 to −0.5

13 If

z = x

− 10xy + y

evaluate z

and z

at the point (2, 3). Hence estimate the change in z as x increases by 0.2 and y

decreases by 0.1.

14 (a) If

f(x, y) = y − x

+ 2x

write down expressions for f

and f

. Hence use implicit differentiation to find dy/dx given that

y − x

+ 2x = 1

(b) Confirm your answer to part (a) by rearranging the equation

y − x

+ 2x = 1

to give y explicitly in terms of x and using ordinary differentiation.

15 Verify that x = 1, y =−1 satisfy the equation x

− 2y

= 3. Use implicit differentiation to find the value

of dy/dx at this point.

16 A function of three variables is given by

f(x

, x

) =+ln(x

)

Find all of the first- and second-order derivatives of this function and verify that

= f

, f

= f

and f

= f

∂

∂x∂y

∂

∂y∂x

∂z

∂y

∂z

∂x

5.1 • Functions of several variables

355

MFE_C05a.qxd 16/12/2005 10:40 Page 355

section 5.2

Partial elasticity and

marginal functions

The ﬁrst section of this chapter described the technique of partial differentiation. Hopefully,

you have discovered that partial differentiation is no more difﬁcult than ordinary differenti-

ation. The only difference is that for functions of several variables you have to be clear at the

outset which letter in a mathematical expression is to be the variable, and to bear in mind that

all remaining letters are then just constants in disguise! Once you have done this, the actual

differentiation itself obeys the usual rules. In Sections 4.3 and 4.5 we considered various

microeconomic applications. Given the intimate relationship between ordinary and partial

differentiation, you should not be too surprised to learn that we can extend these applications

to functions of several variables. We concentrate on three main areas:

 elasticity of demand

 utility

 production.

We consider each of these in turn.

Objectives

At the end of this section you should be able to:

 Calculate partial elasticities.

 Calculate marginal utilities.

 Calculate the marginal rate of commodity substitution along an indifference curve.

 Calculate marginal products.

 Calculate the marginal rate of technical substitution along an isoquant.

 State Euler’s theorem for homogeneous production functions.

MFE_C05b.qxd 16/12/2005 10:40 Page 356

5.2.1 Elasticity of demand

Suppose that the demand, Q, for a certain good depends on its price, P, the price of an alter-

native good, P

, and the income of consumers, Y, so that

Q = f(P, P

, Y )

for some demand function, f.

Of particular interest is the responsiveness of demand to changes in any one of these three

variables. This can be measured quantitatively using elasticity. The (own) price elasticity of

demand is deﬁned to be

=−

with P

and Y held constant. This deﬁnition is identical to the one given in Section 4.5, so

following the same mathematical argument presented there we deduce that

=− ×

The partial derivative notation is used here because Q is now a function of several variables, and

and Y are held constant.

∂Q

∂P

percentage change in Q

percentage change in P

5.2 • Partial elasticity and marginal functions

357

Advice

You may recall that the introduction of the minus sign is an artificial device designed

to make E

positive. This policy is not universal and you are advised to check which con-

vention your own tutor uses.

In an analogous way we can measure the responsiveness of demand to changes in the price

of the alternative good. The cross-price elasticity of demand is deﬁned to be

with P and Y held constant. Again, the usual mathematical argument shows that

=×

The sign of E

could turn out to be positive or negative depending on the nature of the alter-

native good. If the alternative good is substitutable then Q increases as P

rises, because con-

sumers buy more of the given good as it becomes relatively less expensive. Consequently,

> 0

and so E

> 0. If the alternative good is complementary then Q decreases as P

rises, because

the bundle of goods as a whole becomes more expensive. Consequently,

< 0

and so E

< 0.

∂Q

∂P

∂Q

∂P

∂Q

∂P

percentage change in Q

percentage change in P

MFE_C05b.qxd 16/12/2005 10:40 Page 357

Finally, the income elasticity of demand is deﬁned to be

and can be found from

=×

Again, E

can be positive or negative. If the good is superior then demand rises as income rises

and E

is positive. However, if the good is inferior then demand falls as income rises and E

negative.

∂Q

∂Y

percentage change in Q

percentage change in Y

Partial Differentiation

358

Example

Given the demand function

Q = 100 − 2P + P

+ 0.1Y

where P = 10, P

= 12 and Y = 1000, ﬁnd the

(a) price elasticity of demand

(b) cross-price elasticity of demand

Is the alternative good substitutable or complementary?

Solution

We begin by calculating the value of Q when P = 10, P

= 12 and Y = 1000. The demand equation gives

Q = 100 − 2(10) + 12 + 0.1(1000) = 192

(a) To ﬁnd the price elasticity of demand we partially differentiate

Q = 100 − 2P + P

+ 0.1Y

with respect to P to get

=−2

Hence

=− × =− ×(−2) = 0.10

(b) To ﬁnd the cross-price elasticity of demand we partially differentiate

Q = 100 − 2P + P

+ 0.1Y

with respect to P

to get

= 1

∂Q

∂P

192

∂Q

∂P

∂Q

∂Y

MFE_C05b.qxd 16/12/2005 10:40 Page 358

Hence

=×=×1 = 0.06

The fact that this is positive shows that the two goods are substitutable.

Q = 100 − 2P + P

+ 0.1Y

with respect to Y to get

= 0.1

Hence

=× = ×0.1 = 0.52

1000

192

∂Q

∂Y

∂Q

∂Y

192

∂Q

∂P

5.2 • Partial elasticity and marginal functions

359

Practice Problem

1 Given the demand function

Q = 500 − 3P − 2P

+ 0.01Y

where P = 20, P

= 30 and Y = 5000, find

(a) the price elasticity of demand

(b) the cross-price elasticity of demand

If income rises by 5%, calculate the corresponding percentage change in demand. Is the good inferior

or superior?

5.2.2 Utility

So far in this book we have concentrated almost

exclusively on the behaviour of producers. In this

case it is straightforward to identify the primary

objective, which is to maximize proﬁt. We now

turn our attention to consumers. Unfortunately, it

is not so easy to identify the motivation for their

behaviour. One tentative suggestion is that con-

sumers try to maximize earned income. However,

if this were the case then individuals would try to

work 24 hours a day for 7 days a week, which is

not so. In practice, people like to allocate a rea-

sonable proportion of time to leisure activities.

MFE_C05b.qxd 16/12/2005 10:40 Page 359