Jones M., Fleming S.A. Organic Chemistry

Подождите немного. Документ загружается.

5.2 Rings and Strain 189

is cyclopropane’s 60°. Along with this relief,however, comes increased torsional strain,

as there are eight pairs of hydrogens eclipsed as opposed to cyclopropane’s six pairs

(Fig. 5.8). One might estimate the maximum torsional strain in planar cyclobutane

at 8 kcal/mol (1 kcal/mol strain for each pair of eclipsed carbon–hydrogen bonds).

WEB 3D

FIGURE 5.8 There are eight pairs of

eclipsed carbon–hydrogen bonds in

cyclobutane and therefore about

8 kcal/mol of torsional strain.

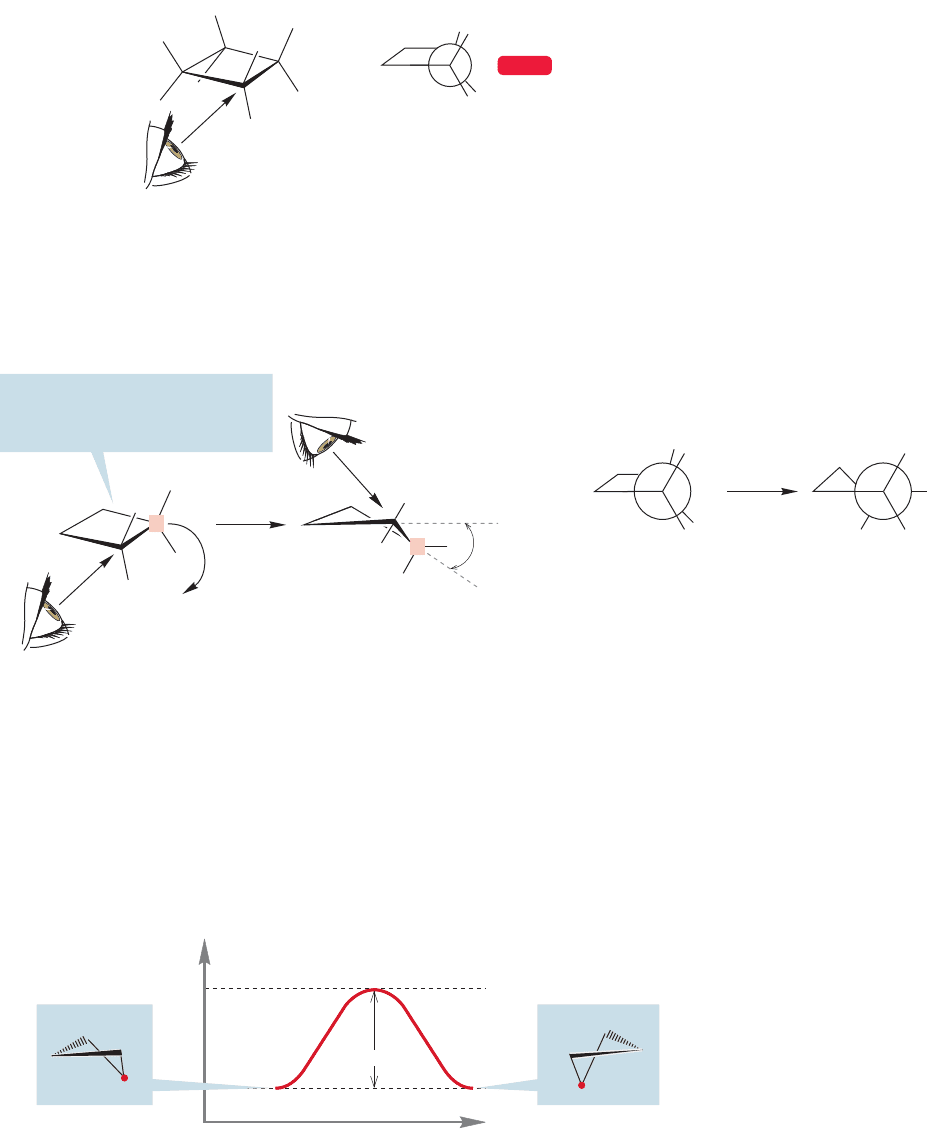
Unlike cyclopropane, cyclobutane has a way to balance torsional and angle

strain. The four-membered ring need not be planar but can distort, or “pucker”

somewhat if this will result in an energy lowering. Let’s look at the consequences

of puckering the ring by moving one methylene group out of the plane of the other

three (Fig. 5.9).

34

In these Newman projections the

red carbon is hidden

Puckering the ring involves

keeping three carbons coplanar

and moving the red carbon down

FIGURE 5.9 Puckering relieves

torsional strain in cyclobutane.

As the ring puckers, torsional strain is reduced, but angle strain is increased. A

balance between the two effects is struck in which the ring puckers about 34° and the

angle closes to about 88°. This form is not static, however; the ring is in

motion through rotation about the carbon–carbon bonds, much as are the acyclic

alkanes.The planar form of cyclobutane is like the eclipsed form of ethane and lies not

in an energy well, but at the top of an energy barrier separating a pair of puckered

cyclobutanes. This barrier is very small, about 1.4 kcal/mol (Fig. 5.10). Cyclobutane

is a mobile, not static, molecule in which different nonplanar forms rapidly intercon-

vert.In Figure 5.10, the bending is exaggerated—the flap is really only 34° out of plane.

Energy

1.4 kcal/mol

The out-of-plane, “down” carbon

is indicated by a red dot

FIGURE 5.10 Mobile cyclobutane.

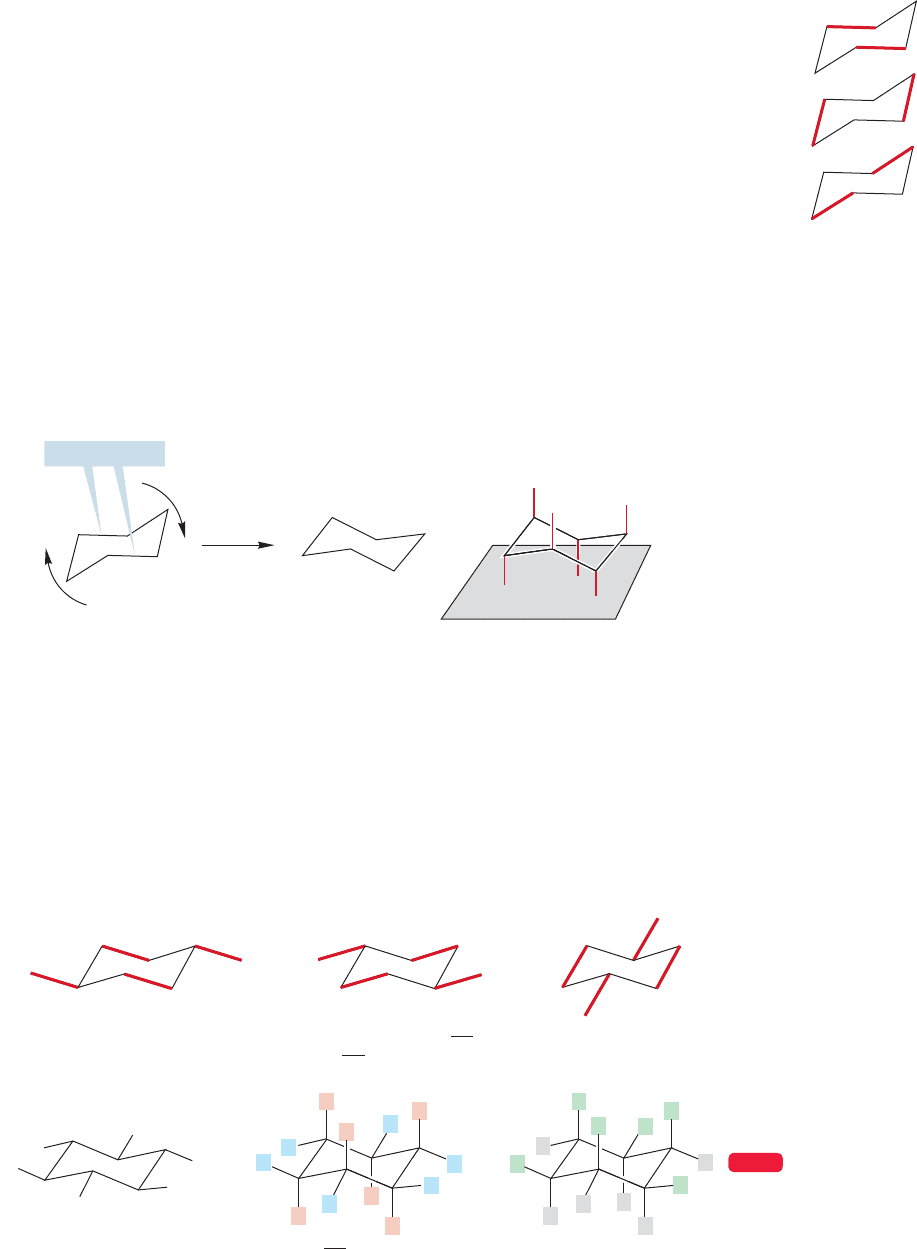
Let’s now look at cyclopentane, (CH

)

,the next cycloalkane,and see how it dis-

torts in a similar way. Were cyclopentane planar, it would suffer the torsional strain

induced by ten pairs of eclipsed hydrogens. The internal angle in a planar pentagon

is 108°, however, so angle strain would be quite small. As in cyclobutane, the ring

distorts from planarity, relieving some eclipsing at the cost of increased angle strain.

For nonplanar cyclopentane, there are two forms of comparable energy, the “enve-

lope” form and the “twist” form (Fig. 5.11).

190 CHAPTER 5 Rings

PROBLEM 5.1 Draw a Newman projection looking down one of the carbon–

carbon bonds in planar and envelope cyclopentane. Use models!

Neither the puckered envelope form nor the twist form of cyclopentane is

static. In the envelope form the “flap” moves around the ring, generating the five

possible puckered isomers. This motion requires only a series of rotations around

carbon–carbon bonds and closely resembles the motions in cyclobutane shown in

Figure 5.10. A model will help you to visualize this motion. Hold two adjacent

carbons, sight down the bond that connects them, and convert one form of the

envelope into another.

By now you must be expecting that a similar distortion from planarity will be

present in cyclohexane, (CH

)

, but you are probably prepared for neither the mag-

nitude of the effect nor its consequences for the structure and stability of all cyclo-

hexanes. In contrast to the smaller rings, distortion from planarity in cyclohexane

relieves both the angle and torsional strain of the planar structure. The internal

angle in a planar hexagon is 120°, larger, not smaller, than the ideal sp

angle of

109.5°. Deviation from planarity will decrease this angle and thus decrease angle

strain. Torsional strain from the twelve pairs of eclipsed carbon–hydrogen bonds

in planar cyclohexane can be expected to contribute about 12 kcal/mol of strain,

which is also decreased in a nonplanar form. So in cyclohexane, both angle and

torsional strain will be relieved by relaxing from a planar structure. Remarkably,

this relaxation produces a molecule in which essentially all of the torsional and

angle strain is gone. The formation of the energy-minimum cyclohexane, called

the “chair” form, is shown in Figure 5.12. The internal angle in real cyclohexane

is 111.5°, close to the ideal angle in a simple straight-chain alkane

(112° in propane), and the carbon–hydrogen bonds are nicely staggered. Newman

projections looking down the carbon–carbon bonds show this, as will (even bet-

ter) a look at a model.

Planar cyclopentane

showing two pairs of

eclipsed hydrogens

The two forms of

nonplanar cyclopentane

Envelope Twist

WEB 3D

FIGURE 5.11 Two distorted

cyclopentanes.

A double Newman projection o

the chair form of cyclohexane;

note the perfect staggering of

the C

H bonds

Chair cyclohexane:

111.5 C

C bond angles;

about 0 kcal/mol of torsional strain

Pull up

Pull down

Planar cyclohexane:

120 C

C bond angles and

about 12 kcal/mol of torsional strain

from C

H bond eclipsing; there is

also angle strain from the too-wide

120 C

C internal angles

FIGURE 5.12 Planar and chair

cyclohexane.

The details of cyclohexane stereochemistry are important enough to warrant a

lengthy discussion (Section 5.4, p. 197), but we can do a few things here in prepa-

ration. First of all, it is necessary to learn to draw a decent cyclohexane. No person

can truly be described as educated unless he or she can do this, and anyone can,

5.2 Rings and Strain 191

regardless of artistic ability. So learn how to do it and the next time your roommate

mentions some obscure European writer, impressing you with his or her erudition

and calling into question your sophistication, confound your tormenter with a

perfectly drawn cyclohexane!

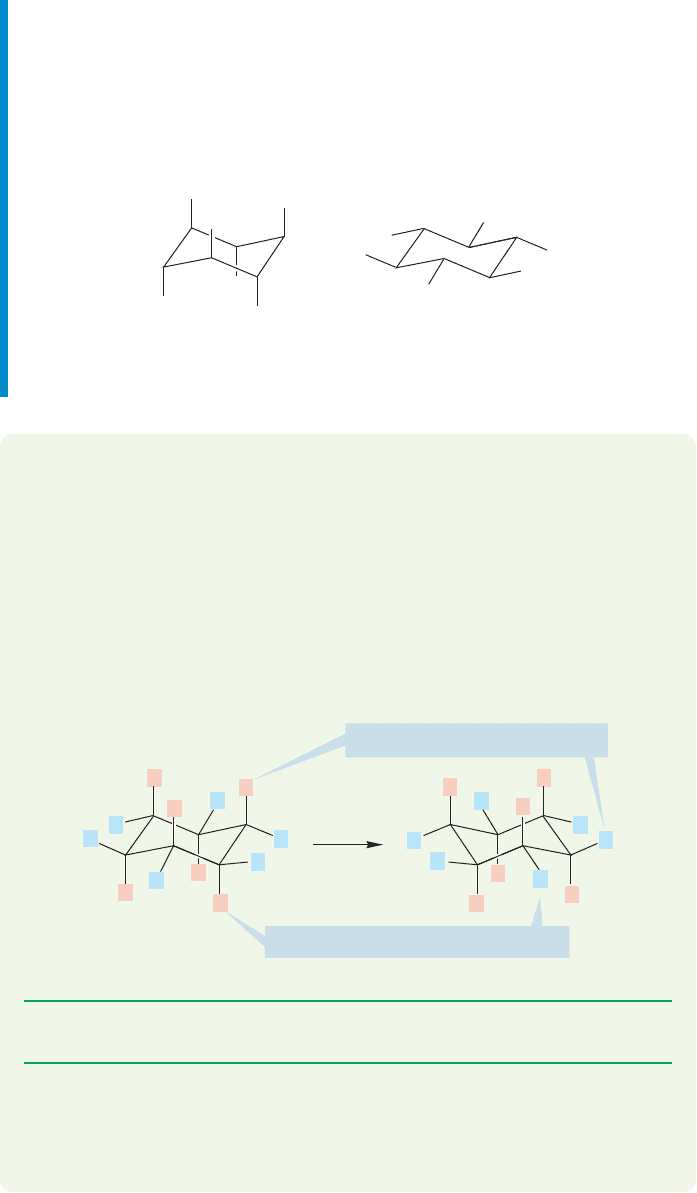
There are a few tricks that make the construction of a perfect drawing easy. First

of all, within the ring, opposite bonds are parallel to each other (Fig. 5.13). With a

little practice, keeping the proper bonds parallel should let you easily draw the

carbon framework of cyclohexane.

It is a bit more difficult to get the hydrogens right. It helps greatly to tip the ring

a little so that the “middle”bonds are not parallel to the top and bottom of the paper

(Fig. 5.14). Now we see the molecule as it would rest on a flat surface. Six of the

carbon–hydrogen bonds are easy to draw; three of them point straight up and three

straight down.The “up”and “down” hydrogens alternate.The hydrogens in these six

bonds are called axial hydrogens, and the bonds to them are called the axial

carbon–hydrogen bonds.

FIGURE 5.13 In chair cyclohexane,

there are three pairs of parallel

carbon–carbon bonds.

tip

Middle bonds

FIGURE 5.14 The set of six “straight

up and down” or “axial”

carbon–hydrogen bonds of chair

cyclohexane are shown in red. All

axial carbon–hydrogen bonds are

parallel.

So far, so good—but it is the positioning of the last six hydrogens, the equa-

torial hydrogens, that gives people the most trouble. To get them right, take

advantage of the parallel carbon–carbon bonds shown in Figure 5.13. Each mem-

ber of this set of six equatorial carbon–hydrogen bonds is parallel to the two

carbon–carbon bonds one bond away.Like the six axial carbon–hydrogen bonds,the

equatorial bonds also alternate up and down, but this set points only slightly up or

slightly down (Fig. 5.15).

The six equatorial hydrogens

of chair cyclohexane

All 12 C

H bonds of chair

cyclohexane; axial hydrogens

are shown in red, equatorial

hydrogens in blue

Up hydrogens in green,

down hydrogens in gray

The three pairs of in-plane or equatorial C

H bonds;

note that they are parallel to the C

C bonds “one bond removed”

WEB 3D

FIGURE 5.15 The equatorial

carbon–hydrogen bonds are parallel

to the ring carbon–carbon bonds one

bond away.The drawing of a perfect

chair cyclohexane is now complete.

192 CHAPTER 5 Rings

Summary

You have learned to draw a perfect cyclohexane ring in its energy-minimum chair

form.This exercise in drawing lets us see one important thing immediately. Note that

there are two different kinds of hydrogen. There is the “straight up and down” set of

six, which are called the axial hydrogens, and the other set of six, which lie roughly

along the equator of the molecule and are called the equatorial hydrogens (Fig.5.16).

WORKED PROBLEM 5.2 It is possible to convert one chair cyclohexane into another.

Get out your models, grasp the two “end” carbons (at the 1 and 4 positions). Move

the carbon that is “up”downward, and move the one that is “down” upward to gen-

erate another chair. You have just “flipped” the ring. We’ll have much more to say

about this process in Section 5.4.What happens to the set of axial hydrogens when

you convert one chair into another? This problem is important and simple.

ANSWER The set of axial hydrogens becomes the set of equatorial hydrogens!

Whether axial or equatorial, an up hydrogen always remains up,however.

Similarly, a down hydrogen is always down, whether axial or equatorial.

The six axial hydrogens

of chair c

clohexane

The six equatorial hydrogens

of chair c

clohexane

FIGURE 5.16 Axial and equatorial hydrogens.

Up axial becomes up equatorial

Down axial becomes down equatorial

ring flip

PROBLEM 5.3 How many carbons will the

C NMR spectrum of cyclohexane reveal?

PROBLEM 5.4 How many hydrogens will the

H NMR spectrum of cyclohexane

reveal? Caution: This problem is much harder than Problem 5.3. Try to find two

answers to this question, one correct at high temperature, the other correct at low

temperature.

Larger rings than cyclohexane will also be nonplanar; but no more spectacular

surprises such as cyclohexane’s energy-minimum form remain to be found. Planar

heptagons and octagons have internal angles of 129° and 135°, respectively, and thus

have substantial angle strain. Both seven- and eight-membered rings would have

5.3 Quantitative Evaluation of Strain Energy 193

severe torsional strain were they to remain planar. There is relaxation to nonplanar

forms, but some amount of strain always remains in these medium-sized rings. It is

a complicated business to analyze medium-sized rings completely, and we will not

embark upon it.Rings with minimal angle strain will have severe interactions—often,

but not always, eclipsings of carbon–hydrogen bonds, and thus substantial torsion-

al strain. Relieving those eclipsings usually induces increased angle strain. As in

cyclopentane, there is a compromise to be made between minimizing angle and tor-

sional strain, and Nature does the best it can, finding the lowest energy structural

compromise. Unlike cyclohexane, however, in the medium-sized rings there is no

obvious low-energy solution. Often there are several somewhat different minima,

close to one another in energy, and separated by quite low barriers.

Fragments of chair cyclohexanes are sometimes seen in the structures of medium-

sized rings. Cyclodecane is an example, as Figure 5.17 shows. Several destabilizing

interactions between carbon–hydrogen bonds should be apparent, especially if you

make a model.

As rings get even bigger, the strain energy decreases. The limit is an infinitely

large ring, which resembles an endless chain of methylene groups. In such a species,

it is possible to stagger all carbon–hydrogen bonds, and, of course, in an infinite ring

there is no angle strain. So after cyclohexane, the next strain-free species is reached

when the ring size has grown large enough to approximate an infinitely large ring.

5.3 Quantitative Evaluation of Strain Energy

Strain is an important factor in chemical reactivity.The more strained a compound,

the higher its energy.The higher in energy a compound,the more likely it is to react.

We have just seen how a combination of torsional and angle strains can act to change

the energy of a ring compound, cyclopropane. Now we move on to some quantita-

tive measures of the energies of ring compounds. We introduce some general

techniques and look ahead to our detailed consideration of energy in Chapter 8.

5.3a Heats of Formation To recapitulate material from Chapter 3 (p. 115), the

heat of formation ( ) of a compound is the enthalpy of its formation by the

reaction of its constituent elements in their standard states.The standard state of an

element is the most stable state at 25 °C and 1 atm pressure. For an element in its

standard state, is taken as zero. The more negative (or less positive) a com-

pound’s , the more stable it is. A negative for a compound means that its

formation from its constituent elements would be exothermic—heat would be liber-

ated. By contrast, a positive means that the constituent elements are more

stable than the compound and its formation would be endothermic—energy would

have to be applied (Fig. 5.18).

¢H °

Cyclodecane

WEB 3D

FIGURE 5.17 A medium-sized ring.

Enthalpy

X + Y

X Y

X + Y

X Y

–

⌬H ⬚

Positive sign

means endothermic

Negative sign

means exothermic

FIGURE 5.18 For a compound more

stable than its constituent elements,

is negative. For a compound less

stable than its constituent elements,

is positive.¢H °

¢H °

194 CHAPTER 5 Rings

Columns 1 and 2 of Table 5.1 collect the heats of formation for some cycloalkanes

and calculate the per methylene group for these hydrocarbons.¢H °

PROBLEM 5.5 How would one get the value of for a CH

group in an infi-

nite chain, (CH

)



? Use the following data to estimate the value of of a

strain-free methylene group in kilocalories per mole: hexane 39.9,

heptane 44.8, octane 49.8, nonane 54.5, decane 59.6 kcal/mol.

¢H °

Note from the final line of Table 5.1 that the for a methylene (CH

) group

in a strain-free straight-chain alkane, (CH

)



, is 4.9 kcal/mol.This value is exactly

the we calculate for a methylene group in cyclohexane. Cyclohexane really is

strain-free.We can now use these data to calculate strain energies for the cycloalkanes.

First, calculate (Table 5.1, column 3) the for the ring constructed from strain-

free methylene groups.The difference between the calculated, strain-free (col-

umn 3) and the real,measured (column 1) is the strain energy (strain E,column 4).

For example, cyclopropane has a measured of 12.7 kcal/mol. A strain-free

cyclopropane ring would have a of 3 4.9 kcal/mol 14.7 kcal/mol.

The difference between these two values (27.4 kcal/mol) is the strain energy

(column 4). The strain energy per CH

(column 5) is (27.4)/3  9.1 kcal/mol.

Now look at the other rings. Cyclopropane and cyclobutane are about equally

strained, although the strain per methylene is significantly higher for cyclopropane.

Cyclopentane and cycloheptane are slightly strained, and the strain gets worse in

the medium-sized rings until we reach a 12-membered ring, in which strain

decreases markedly. Strain continues to decline in the larger rings until (with some

aberrations) we reach the hypothetical strain-free infinite ring.

¢H °

PROBLEM 5.6 Use models to look for the sources of strain in medium-sized

rings.

TABLE 5.1 Strain Energies for Some Cycloalkanes

12 3 4 5

Measured Calcd

per CH

for Strain-free Molecule Strain E Strain E per CH

Molecule (kcal/mol) (kcal/mol) (kcal/mol) (kcal/mol) (kcal/mol)

Cyclopropane 12.7 4.2 14.7 27.4 9.1

Cyclobutane 6.8 1.7 19.6 26.4 6.6

Cyclopentane 18.7 3.7 24.5 5.8 1.2

Cyclohexane 29.5 4.9 29.4 0.1 0

Cycloheptane 28.3 4.0 34.3 6.0 0.9

Cyclooctane 29.7 3.7 39.2 9.5 1.2

Cyclodecane 36.9 3.7 49.0 12.1 1.2

Cyclododecane 55.0 4.6 58.8 3.8 0.3

(CH

)



4.9

≤H °

5.3 Quantitative Evaluation of Strain Energy 195

5.3b Strain Analyzed by Heats of Combustion Strain energies can also be

determined from an analysis of heats of combustion ( ), the energy released—

or consumed—when a compound reacts with oxygen. This method is attractive for

analyzing strain because the measurements can be made and compared directly.

 5 O

3 CO

 4 H

O  Energy

Combustion of a hydrocarbon is an exothermic reaction.The products,H

O and CO

are more stable than the starting hydrocarbon and oxygen.This energy difference, the

exothermicity of the reaction,appears as heat and light (Fig.5.19), which is easily appre-

hended by looking at the light and feeling the heat evolved by a propane stove.

¢H °

530.6 kcal/mol = exothermicity

of this reaction

5 O

3 CO

4 H

O+

Energy

FIGURE 5.19 The combustion of

propane to give CO

O, and

energy.

CONVENTION ALERT

The conventions are confusing here. When writing energy as the product of a

reaction it is conventional to show it as “ energy.”The enthalpy of this exothermic

reaction, ΔH, is negative, however! So, when writing an equation for the reaction,

we say:

 9 O

6 CO

 6 H

O  937 kcal/mol

but, when indicating the enthalpy for the reaction, we say:

 9 O

6 CO

 6 H

O ΔH 937 kcal/mol

Combustion of hydrocarbons can often be used to establish energy differences

between molecules. Compare, for example, the heats of combustion for octane and

an isomer, 2,2,3,3-tetramethylbutane (Fig. 5.20).

A reviewer of this book, RMM, who sat with me (MJ) in chemistry classes at Yale, many, many years ago,

reminds me that we were once told that this molecule, the only isomer of octane with a melting point above

room temperature (mp 104 °C), was known as “solid octane.”We were then told that this was likely to be the

only fact we retained from our organic chemistry course! Now you are stuck with this knowledge.

(solid octane)

+ 12.5 O

8 CO

+ 9 H

O+

FIGURE 5.20 Combustion of two

isomeric octanes.

196 CHAPTER 5 Rings

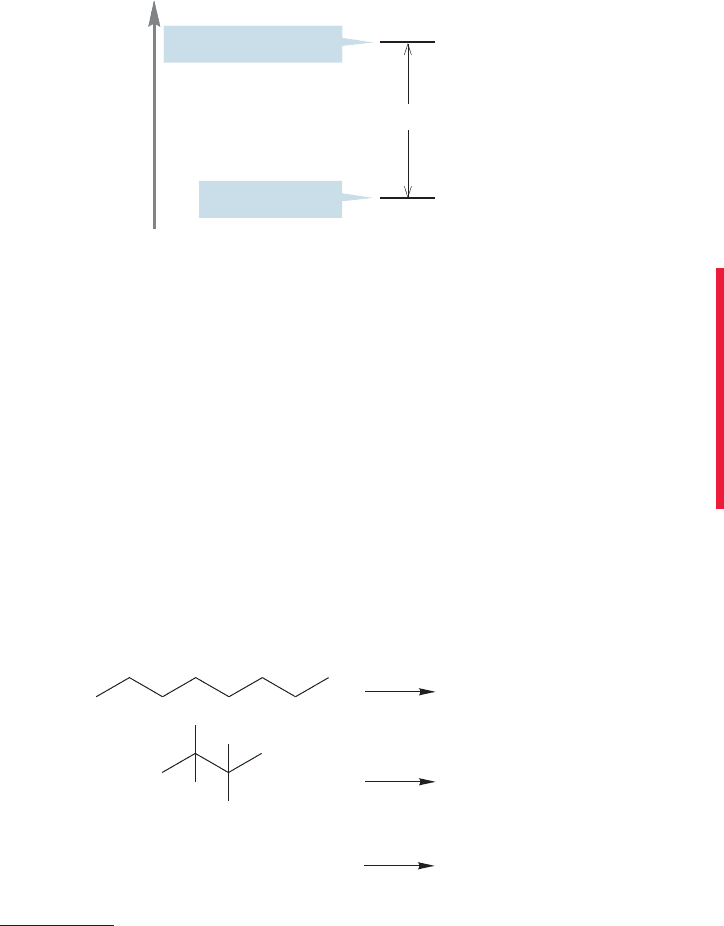
The measured heats of combustion of octane and 2,2,3,3-tetramethylbutane are

1307.60 kcal/mol and 1303.04 kcal/mol, respectively. Figure 5.21 graphically shows

the relationship between these values and the energies of the molecules. Because

these isomeric molecules produce exactly the same products on burning, the differ-

ence in their heats of combustion is the difference in energy between them. Of

course, this analysis also tells you which isomer is more stable, and by how much.

PROBLEM 5.7 The heats of combustion of heptane, 3-methylhexane, and

3,3-dimethylpentane, respectively, are 1149.9, 1148.9, and 1147.9 kcal/mol.

Carefully draw a diagram showing the relative stabilities of these molecules.

We can also use heats of combustion to measure the relative strain energies of

the cycloalkanes. The higher the , the less stable the compound (Fig. 5.22).¢H

8 CO

+ 9 H

Octane

12.5 O

Heat of combustion ( )

1307.60 kcal/mol

Heat of combustion ( )

1303.04 kcal/mol

2,2,3,3-Tetramethylbutane

also, C

12.5 O

This gap is the

energy difference

between these two

isomeric compounds:

4.56 kcal/mol

Energy

1307.60

1303.04

4.56

–

⌬H ⬚

FIGURE 5.21 A quantitative picture

of the combustion of two octanes.

O + CO

166.3

163.9

158.7

157.4

157.5

(CH

)

∞

158.3

158.6

157.8

(kcal/mol)

H 

FIGURE 5.22 The heats of combustion per CH

for a series of cycloalkanes and a strain-free sequence of methylene

(CH

) groups.The higher the heat of combustion, the less stable the compound.

5.4 Stereochemistry of Cyclohexane: Conformational Analysis 197

Once more we need a baseline,and we use the of a strain-free methylene group

in an infinite chain of methylenes,157.5 kcal/mol.This value is determined in much

the same way as was used to get the for a strain-free methylene (p. 194).Then

we measure the values for the series of cycloalkanes, finding the per meth-

ylene for each ring. Subtraction of 157.5 kcal/mol, the of a strain-free meth-

ylene group, gives the strain energy per CH

and, therefore, the strain energy of the

ring compound. As Table 5.2 shows, there is a good correspondence between the

strain energies measured from and . Actually this correspondence is no

surprise, because values are often derived from .¢H

¢H °

TABLE 5.2 Strain Energies for Some Cycloalkanes from and

Measured Strain E per Strain E Strain E

per CH

( −157.5) from from

Molecule (kcal/mol) (kcal/mol) (kcal/mol) (kcal/mol)

Cyclopropane 166.3 8.8 26.4 27.4

Cyclobutane 163.9 6.4 25.6 26.4

Cyclopentane 158.7 1.2 6.0 5.8

Cyclohexane 157.4 0.1 0.6 0.1

Cycloheptane 158.3 0.8 5.6 6.0

Cyclooctane 158.6 1.1 8.8 9.5

Cyclodecane 158.6 1.1 11.0 12.1

Cyclododecane 157.8 0.3 3.6 3.8

(CH

)



157.5

≤H°

≤H °

5.4 Stereochemistry of Cyclohexane: Conformational

Analysis

Earlier, when we were considering the ways in which ring compounds distort so as

to minimize strain, we saw that cyclohexane adopted a strain-free chair conforma-

tion. Now it is time to look at cyclohexane in detail. Six-membered rings are most

common in organic chemistry, and a great deal of effort has been made over the

years at understanding their structure and reactivity. One chair form of cyclohexane

can easily be converted into another. We are now going to look in detail at this

transformation and estimate the energies of the various intermediates and transi-

tion states along the path from one chair to another.This process is an example of

conformational analysis.

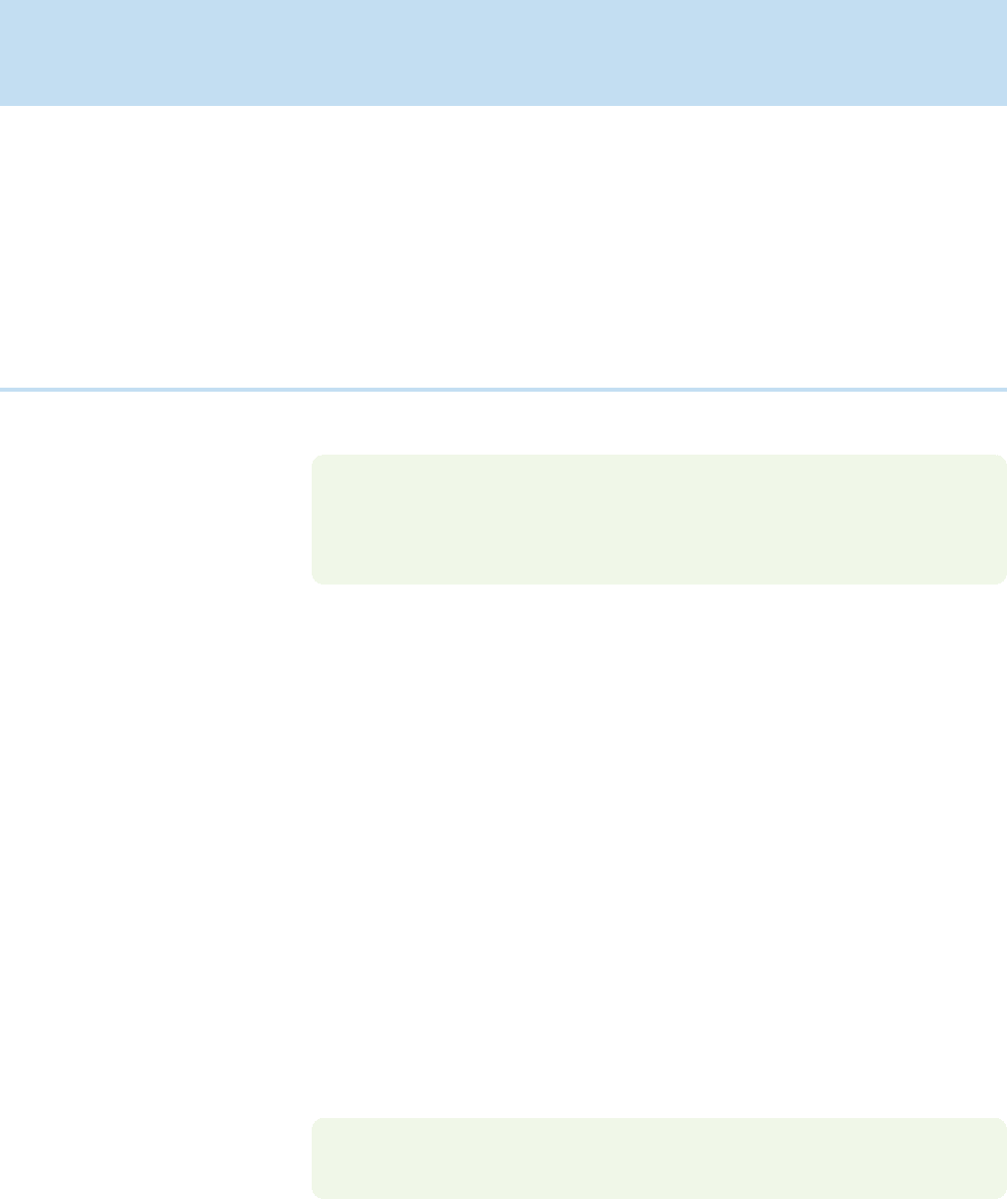
A little manipulation of a model will show the overall conversion, but it’s not

easy to come to the actual pathway for the process. If we move carbons 1, 2, 3, and

4 in Figure 5.23 into one plane, with carbon 6 above the plane and carbon 5 below

the plane, we come to a “half-chair” structure.

Chair Half-chair

(transition state)

Twist

or twist-boat

FIGURE 5.23 Conversion of

the energy-minimum chair

cyclohexane into the half-

chair and then the twist form.

198 CHAPTER 5 Rings

The half-chair conformation does not represent a stable molecule, but is instead

a picture of the top of the energy “mountain pass” (a transition state) leading to a

lower energy molecular “valley” called the twist conformation or, sometimes the

twist-boat conformation (Fig. 5.23). The half-chair contains many eclipsed

carbon–hydrogen bonds,which become staggered somewhat in the twist conforma-

tion, and angle strain is partially relieved as well. The twist conformation can pass

through a second half-chair to give another chair cyclohexane.Kinetic measurements

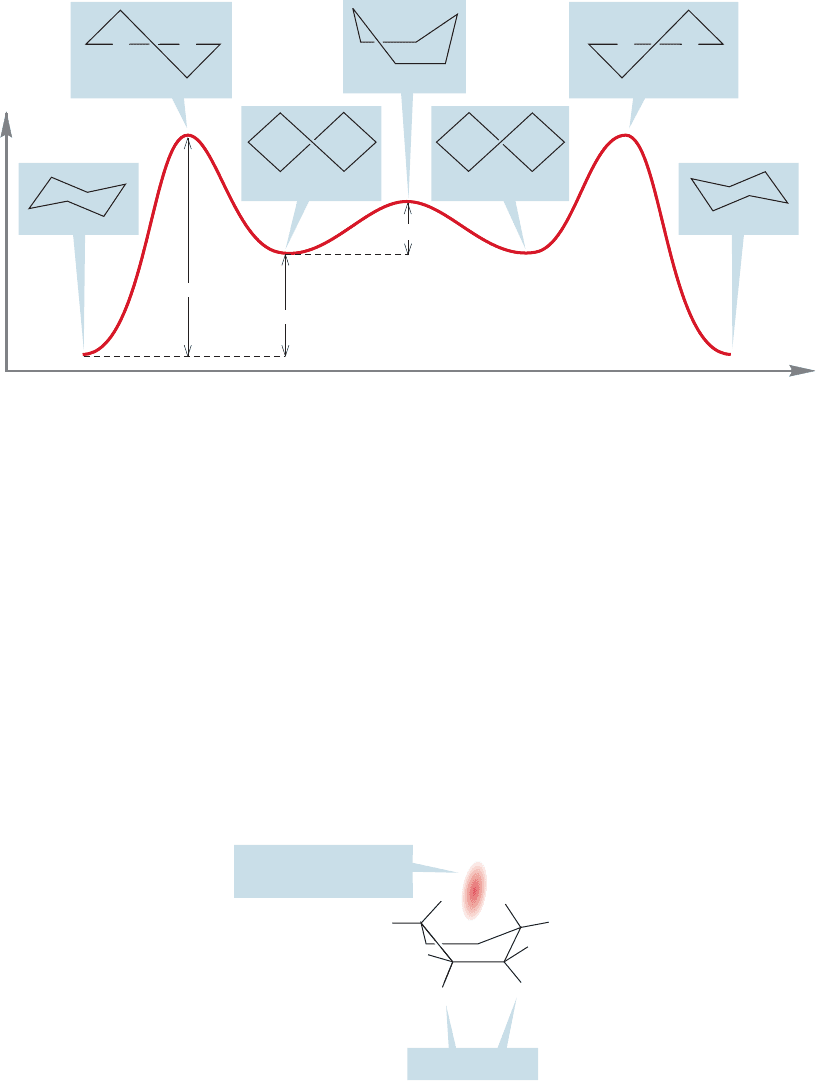
allow an evaluation of the energies involved (Fig. 5.24).The half-chair and the twist

lie 10.8 and 5.5 kcal/mol above the chair, respectively.

Energy

Chair

Twist

Half-chair

10.8 kcal/mol

5.5 kcal/mol

1.5 kcal/mol

Full-boat

C C

Twist

Half-chair

FIGURE 5.24 The interconversion of two chair cyclohexanes. The two chairs and the two twist forms

are intermediates (energy minima), and the two half-chairs and the full-boat are transition states

(energy maxima).

Do not confuse the twist with the full-boat shown at the top of a “mountain” in

Figure 5.24. The full-boat is not an energy minimum but is, like the half-chair, an

energy maximum. It lies at the top of the energy barrier (like the half-chair, it, too,

is a transition state) separating two twist forms. The full-boat is only 1.5 kcal/mol

higher than the twist (7.0 kcal/mol higher than the chair), and can never be isolat-

ed because it is not an energy minimum.

Both the half-chair and the full-boat suffer from the kinds of strain we have seen

before. In the half-chair, much of the ring is planar, and there is both angle and tor-

sional strain. The full-boat also has angle and torsional strain, but there is another

hydrogen–hydrogen interaction that is destabilizing.This new interaction is between

the “prow” and “stern” carbons and between the two “inside”hydrogens at the prow

and stern of the boat.This new kind of strain is induced when two atoms come too

close to each other and is called van der Waals strain (Fig. 5.25).

“Boat” cyclohexane

Torsional strain

Steric repulsion:

van der Waals strain

FIGURE 5.25 van der Waals strain in

the full-boat form of cyclohexane.

Don’t confuse this strain with

attractive van der Waals forces (p. 87).