Кармелюк Г.І. Теорія ймовірностей та математична статистика
Подождите немного. Документ загружается.

311
4.4. Функція розподілу імовірностей випадкової
величини та її властивості
Інтегральною
або функцією розподілу називають
функцію F(x), яка визначає імовірність того, що випадкова
величина Х в результаті випробування набуде значення, яке
строго менше, ніж х: F(x) = P(X < x) (4.4.1).
1. Область визначення функції розподілу – множина всіх
дійсних чисел, а область значень – відрізок [0; 1].
2. F(x) – неспадна функція, тобто
)()(
12
xFxF ≥ , якщо
12
xx >
.
Наслідок 1. Імовірність того, що випадкова величина Х
набуде значення з проміжку [а, b], дорівнює різниці
інтегральних функцій на кінцях цього проміжку:
)()()( aFbFbXaP
−
=≤≤ (4.4.2).
Наслідок 2. Імовірність того, що неперервна випадкова
величина Х при випробуванні набуде одне певне значення до-
рівнює нулю.
3. Якщо можливі значення випадкової величини Х нале-
жать інтервалу [a, b], то: 1) F(x) = 0 при
a
x
≤
; 2) F(x) = 1 при
bx ≥ .
Наслідок. Якщо можливі значення неперервної випадко-
вої величини Х розташовані на всій числовій осі, то вико-
нуються такі граничні співвідношення:
0)(lim =
−∞→
xF
x
; 1)(lim
=
∞→
xF
x
(4.4.3).
Якщо ж неперервна випадкова величина означена в
інтервалі [a, b], то граничні співвідношення мають такий
вигляд
0)(lim
0
=
−→
xF
ax
, 1)(lim
0
=
−→
xF
bx
.
Графіком інтегральної функції є крива, що обмежена пря-
мими y = 0 і y = 1.

312
Задачі
4.4.1. Кидають три монети.
Потрібно:
а) задати випадкову величину X, яка рівна числу випадань
“номіналу”;
б) побудувати ряд розподілу і функцію розподілу F(х)
величини X, якщо ймовірність випадання “герба” рівна 0,5.
Розв’язок.
а) Нехай випадкова величина Х – число випадань номіна-
лу. У трьох випробуваннях n = 3 (підкидають три монети),
номінал може
випасти Х = 0, 1, 2, 3 число разів. Відповідні
імовірності обчислимо згідно формули Бернуллі:
;)(
xnxx
nn
qpCxP
−
=
5,05,011
=
−
=
−
=
pq
;
;125,05,011)0(
30300
3
=⋅⋅===
−
qpCxP
;375,05,05,03)1(
31311
3
=⋅⋅===
−
qpCxP
;375,05,05,03)2(
222
3
=⋅⋅=== qpCxP
(
)
.125,015,01)3(
3
033
3
=⋅⋅=== qpCxP
Перевірка:
0,1125,0375,0375,0125,0 =+++=
∑
i
p .
Отже, закон розподілу Х має вигляд:
Х
0 1 2 3
Р
0,125 0,375 0,375 0,125
1. Якщо 0≤x , то 0)(
=
xF . Дійсно, значень менших
числа 0 величина х не приймає. Отже, при Х < 0 функція
0)()( =≤= xXPxF .
2. Якщо
10
<
≤ x , то 125,0)(
=
xF . Дійсно, Х може
прийняти значення 0 з імовірністю 0,125.
3. Якщо
21
<
≤ x , то
5,0)(
=
xF
. Дійсно, Х може прий-
няти значення 0 з імовірністю 0,125 і значення 1 з імовірністю
0,375. Отже, одне з цих значень, байдуже яке, Х може прий-
няти (за теоремою додавання імовірностей несумісних подій)
з імовірністю 0,125 + 0,375 = 0,5.
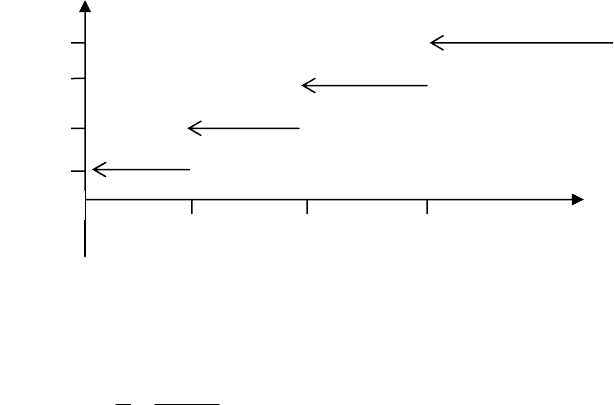
313
4. Якщо 31
<
≤ x , то 875,0)(
=
xF . Дійсно, Х може
прийняти значення 0 з імовірністю 0,125; значення 1 з імовір-
ністю 0,375 і значення 2 з імовірністю 0,375. Отже, одне з цих
значень, байдуже яке, Х може прийняти (за теоремою дода-
вання імовірностей несумісних подій) з імовірністю 0,125 +
+ 0,375 + 0,375 = 0,875.
5. Якщо х > 3, то
1)(
=
xF . Дійсно, подія 3
≤
X – досто-
вірна і її імовірність рівна 1.
Таким чином, інтегральна функція розподілу має вигляд:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
≤<
≤<
<
=
.31
,32875,0
,215,0
,10125,0
,00
)(
x
x
x
x
x
xF
На рис. 4.4.1 наведений графік цієї функції:
Рис. 4.4.1.
4.4.2. Випадкова величина Х задана на всій осі ОХ функ-
цією розподілу
π
arctgx
xF +=
2
1
)(
.
х
1
2
3
0
,
125
0
0
,
5
0
,
875
1
,
0
)(xF

314
Знайти ймовірність того, що в результаті випробування
величина Х прийме значення з інтервалу (0; 1).
Розв’язок.
π
arctgx
xF +=
2
1
)(
. Для знаходження шуканої імовірнос-
ті використаємо формулу
)()()(
α
β
β
α
FFXP
−
=
≤
≤
.
Отже,
=−−+=−=≤≤
π
π
0
2
11
2
1
)0()1()10(
arctgarctg
FFXP
4
1
0
4
=−
⋅
=
π
π
.
4.4.3. Випадкова величина Х задана функцією розподілу:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
1
2
arcsin
2
1
0
)(
π
x
xF
Знайти ймовірність того, що в результаті випробування
величина Х прийме значення, яке належить інтервалу (–1; 1).
Розв’язок.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−+
−≤
=
.2при1
;22
2
arcsin
1
2
1
;2при0
)(
x
x
x
x
xF
π
−−+=−−=≤≤−
2
1
2
1
arcsin
1
2
1
)1()1()11(
π
FFXP
3
1
6
2
6
1
6
1
2
1
arcsin
1
==
⎟
⎠
⎞
⎜
⎝
⎛
−⋅−⋅=
⎟
⎠
⎞
⎜
⎝
⎛
−−
π
π
π
ππ
.
при 2
−
≤
x ;
при
22
≤
<
−
x ;
при
2>x
.

315
4.4.4. Випадкова величина Х задана на всій осі ОХ функ-
цією розподілу:
π
2
arctg
2
1
)(
x
xF +=
.
Знайти можливе значення х
1
, що задовольняє умову: з
ймовірністю 1/4 випадкова величина Х в результаті випро-
бування прийме значення, більше х
1
.
Розв’язок.
Події
)(
1
xX ≤ і )(
1
xX > – протилежні, тому
1)()(
11
=
>+≤ xXxXP . Звідки
6
1
)(1)(
11
=≤−=> xXxXP
згідно умови задачі. Отже,
6
5
6
1
1)(
1
=−=≤ xXP . Але подія
)()()(
111
xXxXxX
<
+
==≤ – сума несумісних подій, то-
му
)()()()(
1111
xXPxXPxXPxXP
<
=
<
+
=
=≤ , оскільки
0)(
1
== xXP , як імовірність того, що неперервна випадкова
величина приймає конкретне значення х. За означенням
2
1
2
1
)()(
1
11
x
arctgxFxXP
π
+==< . Отже, ×+=
π
1
2
1
6
5
2
1
x
arctg×
, або
32
1
π
=
x
arctg , звідки 3
2
1
=
x
, або 32
1
=x .
4.4.5. Випадкова величина Х задана функцією розподілу:
⎪
⎩
⎪
⎨
⎧
=
1
0
)(
2
xxF
Знайти ймовірність того, що в результаті 4 незалежних
випробувань величина Х рівно 3 рази прийме значення, що
належить інтервалу (0,25; 0,75).
при х
≤
0;
при 0 < х
≤
1;
при х > 1.

316
Розв’язок.
Нехай подія А полягає в тому, що в 4 незалежних ви-
пробуваннях подія настає три рази. Обчислимо спочатку
імовірність того, що випадкова величина попадає в заданий
інтервал:
==−=≤≤=
75,0
25,0
2
)25,0()75,0()75,025,0( xFFXPp
.5,00625,05625,0)25,0()75,0(
22
=−=−=
Тоді імовірність події А обчислимо згідно формули
Бернуллі:
qpCP
33
44
)3( = , де р = 0,5; q = 0,5.
Отже,
25,05,05,0
)!34(!3
!4
)3(
3
4
=⋅⋅
−
=P .
4.4.6.. Точку кидають навмання всередину кулі радіуса R.
Ймовірність її попадання в будь-яку область, розташовану в
середині кулі, пропорційна об'єму цієї області.
Знайти функцію розподілу, щільність ймовірності, мате-
матичне сподівання і дисперсію віддалі від точки до центру
кулі.
Розв’язок.
Нехай випадкова величина Х – віддаль від точки до цент-
ру кола. Згідно умови задачі Rx
≤
≤
0 . Тоді ймовірність то-
го, що точка попаде всередину кулі радіуса х рівна відно-
шенню об’ємів куль радіусів х і R:
.
3
4
3
4
)(
3
3
3
3
R
x
R
x
xXP ==≤
π
π
А згідно означення, це є інтегральною функцією
розподілу ймовірності.
317
Отже,
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
<
≤<
=
.при1
;0при0
;0,
)(
3
3
Rx
x
Rx
R
x
xF
Щільність ймовірності
/
3
3
/
)()(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==
R
x
xFxf
.
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥
≤≤
≤
=
.при0
;0,
3
;0,0
)(
3
2
Rx
Rx
R
x
x
xf
Тоді математичне сподівання М(Х) і дисперсія D(Х)
віддалі від точки до центру кулі рівні:
=⋅=⋅=⋅=
∫∫
R
RR
x
R
dxxx
R
dxxfxXM
0
4
3
2
0
3
0
4
33
)()(
;
4
3
4
3
4
3
RR
R
==
−⋅⋅=−=
∫∫
dxx
R
x
R
XMdxXfxXD
RR
2
3
2
0
3
22
0
33
)()()(
.
80
3
16
9
5
3
4
3
5
3
4
3
22
3
5
2
0
5
3
2
RR
R
R
R
x
R
R
R
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
4.4.7. Випадкова величина X розподілена за законом Ре-
лея з щільністю ймовірності:
⎪
⎩
⎪
⎨
⎧
×
=
−
0
)(
2
2
2
2
σ
σ
x
e
x
xf
Знайти:
при x>0 )0( >
σ
,
при
0
≤
x .
318
а) функцію розподілу випадкової величини X;
б) моду і медіану цього розподілу.
Розв’язок.
а) Інтегральна функція розподілу визначається за форму-
лою:
==+==
∫∫∫∫
−
∞−∞−
x
x
xx
dxe
x
dxxfdxxfdxxfxF
0
2
2
0
0
2
2
)()()()(
σ
σ
.1
22
2
2
2
2
2
2
2
2
2
0
2
0
2
2
2
0
2
2
2
σσσσ
σσ
x
x
x
x
x
x
x
ee
x
de
x
de
−−−−
−==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−=
∫∫
б) Мода, як значення випадкової величини при якому
функція щільності досягає максимуму знаходиться з умови
0)(
/
=xf . В результаті диференціювання отримуємо вираз:
[]
.0
11
2
21
22
2
222
22
2
22
2
2
2
=−⋅=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅−
−−−
xe
x
xee
xxx
σ
σσσσ
σσσ
Отже,
22
σ
=x
, або
σ
=
x
. Таким чином, .
σ
=
Mo
Значення медіани знаходиться з умови:
=
≤
)( MexP
,
2
1
)( =≥= MexP .
2
1
)( =MeF
Підставимо Х = Ме у вираз інтегральної функції:
2
1
1
2
2
2
=−
−
σ
Me
e або
2
1
2
2
2
=
−
σ
Me
e .
Прологарифмуємо вираз і отримуємо:
2ln2
22
σ
=Me , отже
σσ
18,12ln2 ≈=Me .
в) Математичне сподівання М(Х) випадкової величини Х
рівне:
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−=⋅=
∫∫
∞
−
∞
−
0
2
2
2
0
2
2
2
)(
2
2
2
2
σσ
σσ
x
dxedxe
x
xXM
xx
319
==−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∫∫∫
∞
−
∞
−
∞
−
∞
−
0
2
0
2
0
2
0
2
2
2
2
2
2
2
2
2
dxedxexeexd
xxxx
σσσσ
.
2
2
;
0
2
0
2
2
2
2
π
σσσ
σ
σ
σ
σ
⋅===
=
⋅==
=
∫∫
∞
−
∞
−
dzedze
dzdx
zxz
x
z
x
2
2
2
2
0
2
2
2
π
π
=
=
−
∞
−
∞
∞−
∫
∫
dze
dze
z
z
– інтеграл Пуассона;
0
2
2
limlim
2
2
2
2
2
2
2
==
∞→∞→
σσ
σ
x
x
x
x
xee
x
.
г) Дисперсія рівна:
);()()(
22
0
XMdxxfxXD −=
∫
∞
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=⋅=
−
∞∞
−
∫∫
2
2
2
2
2
2
00
2
2
22
)(
σσ
σ
xx
edxdxe
x
xXM
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−=+−=
∫∫
∞
−
∞
−
∞
−
0
2
2
2
2
0
2
0
2
2
2
22
2
2
2
2
2
2
σ
σ
σσσ
x
dedxxeex
xxx
=−=⋅=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
−
∞→
∞
−
∞
−
∫
2
2
2
2
2
2
2
2
2
0
2
2
0
2
2
2
2
2
lim22
2
2
σ
σσ
σ
σσ
σ
σ
x
x
xx
e
e
x
de
.202
22
σσ
=−=
Отже,
=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
2
2
2
2
2)(
2
2
2
2
πσ
σ
πσ
σ
XD

320
.4292,0
2
)4(
2
2
σ
πσ
≈
−
=
4.4.8. Випадкова величина Х задана функцією розподілу:
при x
≥ x
0
(x
0
> 0)
при x
0
< x .
Знайти математичне сподівання, дисперсію і середнє
квадратичне відхилення Х.
Розв’язок.
Математичне сподівання неперервної випадкової величи-
ни задається формулою :
dxxfXM
b
a
)()(
∫
= . Отже, необхід-
но від інтегральної функції F(x) перейти до диференціальної:
⎪
⎩
⎪
⎨
⎧
<
>≥
==
.при0
);0(при3
)()(
0
00
4
3
0
xх
xхх
x
x
xFxf
I
Обчислимо математичне сподівання М(Х):
=⋅−===
∞
∞∞
∫∫
0
00
2
3
0
3
3
0
4
3
0
1
2
3
33)(
x
xx
x
x
x
dx
xdx
x
x
xXM
.
2
3
2
3
0
1
2
31
2
3
lim
00
2
3
0
2
3
0
xx
x
x
x
x
x
=+=⋅+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅−=
∞→
Дисперсія D(Х) визначається за формулою:
−=−⋅=
∫∫
∞∞
4
2
3
0
22
00
3)()()(
x
dxx
xXMdxxfxXD
xx
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=−−=−=
⎟
⎠
⎞
⎜
⎝
⎛
−
∞→
∞
∞
∫
x
x
x
x
x
x
x
dx
xx
x
x
x
3
0
2
0
3
0
2
0
2
3
0
2
0
3
lim
4
93
4
9
3
2
3
0
0
⎪
⎩
⎪
⎨
⎧
−
=
0
1
)(
3
3
0
x
x
xF
