Кармелюк Г.І. Теорія ймовірностей та математична статистика
Подождите немного. Документ загружается.

301
−
+
−=+ 884499112,5442249555,3)731085651,1
.0000,1442249568,1 =−
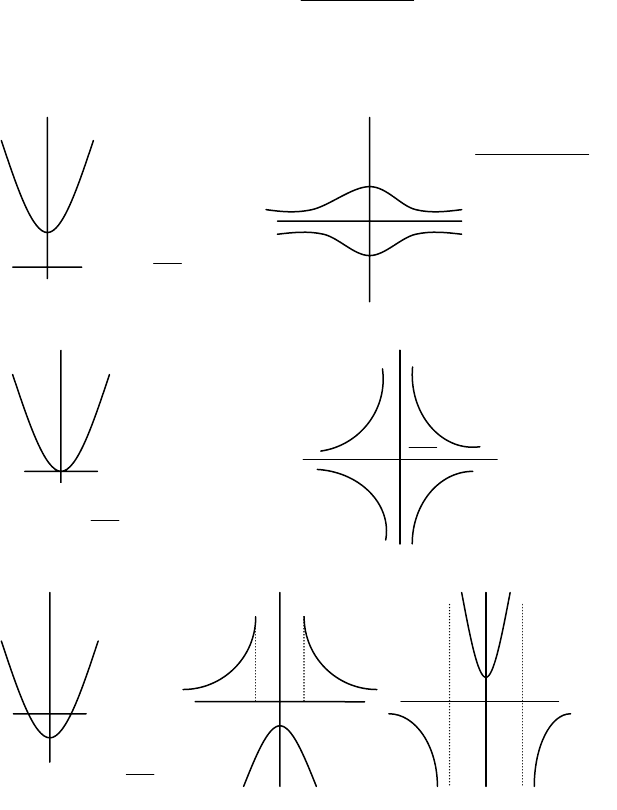
е) Графік функції
cbxax
d
xf
++
=
2
)( в залежності від
знаку параметра d і дискримінанта D має вигляд (рис. 4.3.3є-
і):
Рис. 4.3.3е
Рис. 4.3.3є
Рис. 4.3.3ж
0>d
0<d
0
,0
>
>
D
a
3)
0
,0
>
>
D
a
a
b
x
2
−=
х
1
х
2
х
1
х
2
a
b
x
2
−=
0>d
0
<
d
0
,0
=
>
D
a
2)
0
,0
=
>
D
a
a
b
x
2
−=
a
b
x
2
−=
0,0
2
<>
++=
Da
cbxaxy
cbxax
d
xf
+
+
=
2
)(
0>d
0
<
d
0
,0
<
>
D
a
1)
302
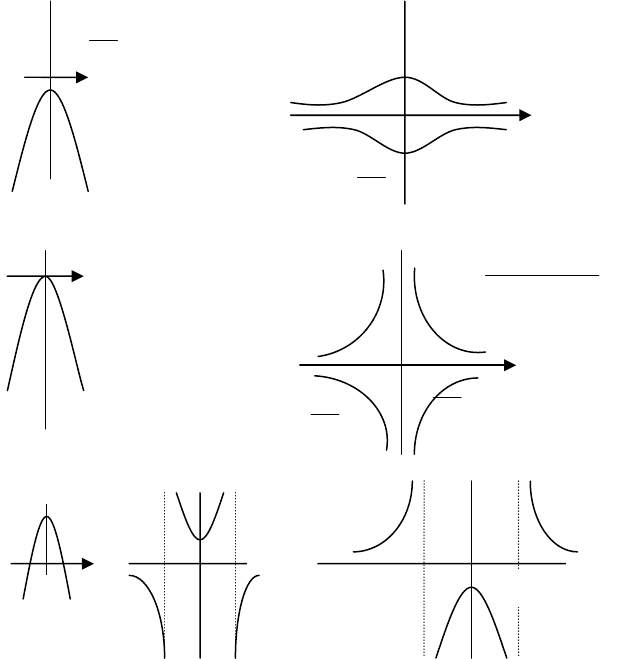
Рис. 4.3.3з
Рис. 4.3.3и
Рис. 4.3.3і
Оскільки функція щільності додатня, то нас будуть ціка-
вити ті випадки, де функція розташована над віссю Х. Виді-
лимо повний квадрат у знаменнику і використаємо влас-
тивість функції щільності:
a
b
x
2
−=
0>d
0
<
d
5)
a
b
x
2
−=
cbxax
d
xf
+
+
=
2
)(
cbxaxxf
Da
++=
=<
2
)(
0,0
cbxaxy
Da
++=
<
<
2
0,0
0>d
0
<
d
0
,0
<
<
D
a
4)
a
b
x
2
−=
a
b
x
2
−=
х
1
х
2
х
0
0
>
<
D
a
6)
х
х
2 х
1
0
0
0
>
>
<
d
D
a
х
1
х
2
х
0
0
0
<
>
<
d
D
a
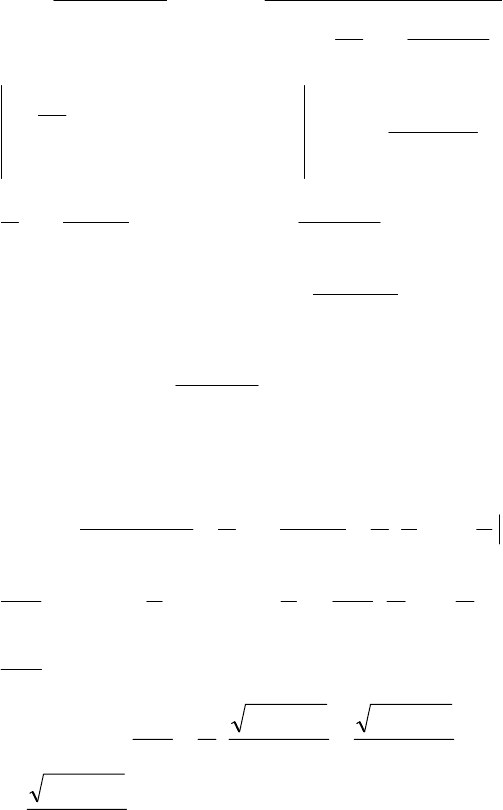
303
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
⎟
⎠
⎞
⎜
⎝
⎛
+
=
++
∫∫
∞
∞−
∞
∞−
2
2
2
2
4
4
2 a
bac
a
b
xa
dx
ddx
cbxax
d
[]
=
±
⋅=
−∞→−∞→∞→∞→
==+
=
∫
∞
∞−
22
;;;
;;
2
kta
dt
d
txtx
dtdxt
a
b
x
,
22
kt
dt
a
d
±
⋅=
∫
∞
∞−
де позначено .
4
4
2
2
2
k
a
bac
±=
−
Знак плюс береться тоді, коли
0
4
4
2
2
>
−
a
bac
, тобто D < 0,
а отже, корені тричлена ах
2
+ bх + с – комплексні; знак мінус
береться тоді, коли
0
4
4
2
2
<
−
a
bac
, тобто D > 0, тобто корені
тричлена ах
2
+ bх + с – дійсні.
1. Нехай D < 0 (рис 4.3.3е: а > 0, d > 0 і рис 4.3.3з: а < 0,
d < 0), тоді:
=⋅=
±
⋅=
++
⋅
∞
∞−
∞
∞−
∞
∞−
∫∫
k
t
arctg
ka
d
kt
dt
a
d
cbxax
dx
d
1
222
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−−
⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅
=
−∞→∞→
22
limlim
ππ
ka
d
k
t
arctg
k
t
arctg
ka
d
tt
.1=⋅
⋅
=
π
k
a
d
Звідки,
;
2
4
2
4
22
πππ
bac
a
bacaka
d
−
=
−
⋅=
⋅
=
π
2
4
2
bac
d
−
=
, причому а і d одного знаку.
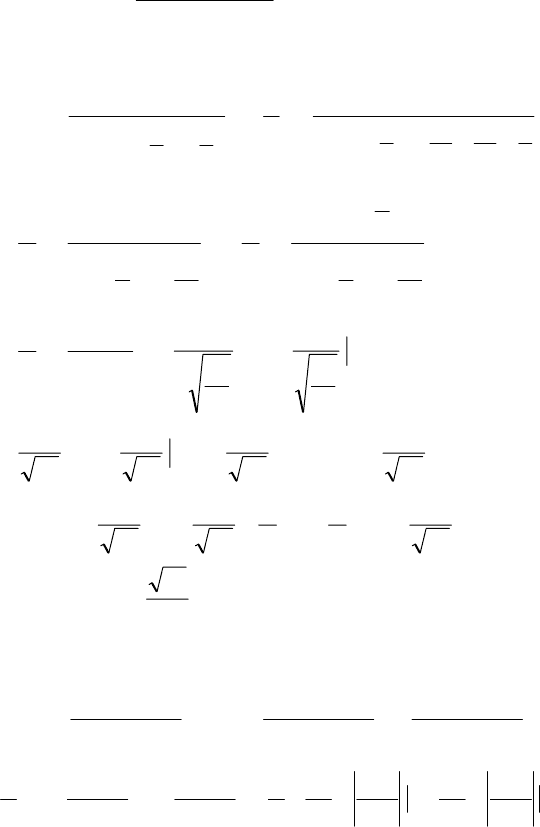
304
Приклад. Обчислити значення параметра d при якому
функція
332
)(
2
−
+
−
=
x
x
d
xf
є щільністю.
У знаменнику виділимо повний квадрат винісши
параметр а = 2 за дужки.
=
+−+⋅−
⋅−=
⎥
⎦
⎤
⎢
⎣
⎡
+−−
⋅
∫∫
∞
∞−
∞
∞−
2
3
16
9
16
9
4
3
2
2
2
3
2
3
2
2
2
xx
dxd
xx
dx
d
=
+
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅−=
+
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅−=
∫∫
∞
∞−
∞
∞−
16
15
4
3
4
3
2
16
15
4
3
2
22
x
xd
d
x
dxd
=−=
+
⋅−=
∞
∞−
∞
∞−
∫
16
15
16
15
2
2
22
t
arctg
d
kt
dtd
⎜
⎝
⎛
−⋅−=−=
∞→
∞
∞−
15
4
lim
15
2
15
4
15
2 t
arctg
dt
arctg
d
t
.1
15
2
22
15
2
15
4
lim =⋅−=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−−⋅−=
⎟
⎠
⎞
−
−∞→
π
ππ
ddt
arctg
t
Звідки
π
2
15
−=d
, параметри а і d – від’ємні.
2. Нехай D > 0 (рис 4.3.3ж: а > 0, d > 0 і рис 4.3.3і: а < 0,
d < 0), тоді:
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
++
+
++
⋅=
++
⋅
∫∫∫
∞
∞−
∞
∞−
2
1
222
x
x
cbxax
dx
cbxax
dx
d
cbxax
dx
d
.ln
2
1
ln
2
1
2
1
2
1
2222
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
+
−
⋅=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
−
⋅=
∞
∞−
∞
∞−
∫∫
t
t
t
t
kt
kt
kkt
kt
ka
d
kt
dt
kt
dt
a
d
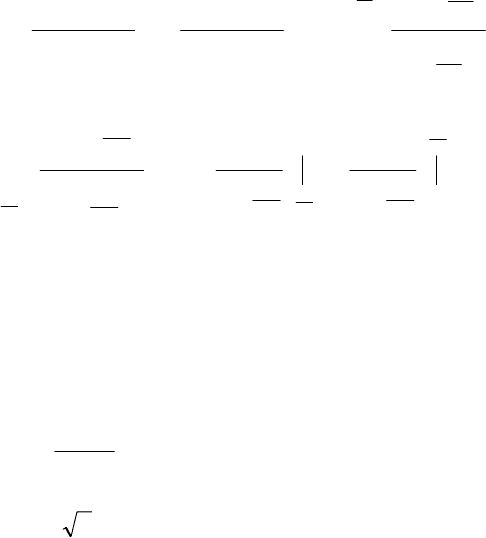
305
Оскільки інтеграли в квадратних дужках розбіжні (не
мають границь), то функція з квадратним тричленом у якого
D > 0, диференціальною бути не може.
3. Нехай D = 0 (рис 4.3.3є: а > 0, d > 0 і рис 4.3.3и: а < 0,
d < 0), тоді:
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅=
⎥
⎦
⎤
⎢
⎣
⎡
++
+
++
⋅
∫∫∫
−−
∞−
∞
+
−
∞−
ε
ε
ε
a
b
x
x
a
b
x
a
b
xd
d
cbxax
dx
cbxax
dx
d
2
2
22
2
2
.
2
1
2
1
2
2
2
2
2
2
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
+
⋅=
⎥
⎥
⎥
⎥
⎦
⎤
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
+
+−
∞
∞−
−−
∞
+−
∫
ε
ε
ε
a
b
a
b
a
b
a
b
x
a
b
x
d
a
b
x
a
b
xd
Оскільки вирази в дужках не мають границь, тобто є
розбіжними, то функція, тричлен якої має D = 0, не може бути
функцією щільності.
4.3.15. Якій з трьох запропонованих лотерей
L
1
(36;0,44;41), L
2
(100;0,8;150), L
3
(100;0,2;150), особа надасть
перевагу, якщо її функція корисності задається формулами:
а) U(x) =
7
32 −х
;
б) U(x) = x
4
;
в)
U(x)
=
4
x ?
Обчислити премію за ризик.
Вказівка. Згідно з основним положенням теорії корис-
ності, суб’єкт керування, що приймає рішення в умовах не-
визначеності та породженого нею ризику, повинен макси-
мізувати сподіване значення корисності результатів.
Розв’язок
1.
Обчислимо сподіваний виграш у лотереї з дискретни-
ми виграшами за формулою:
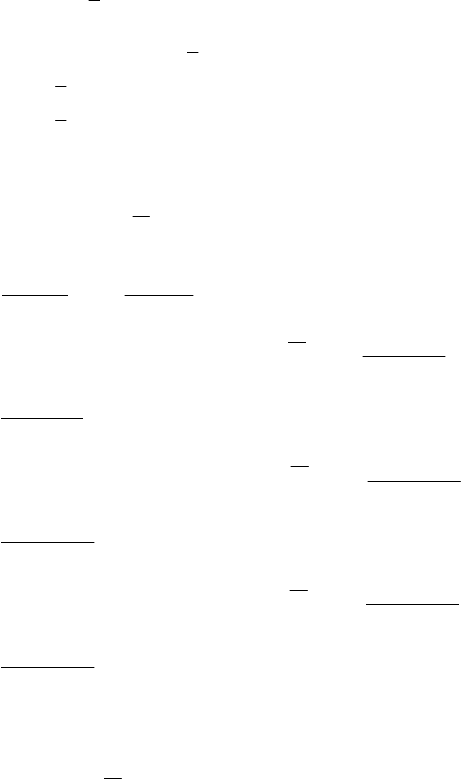
306
М(Х) =
х
=
∑
=
2
1
i
ii
px .
Для лотереї – L
1
:
1
x
= 36 · 0,44+41· 0,56 = 38,8;
L
2
:
2
x = 100 · 0,8+150 · 0,2 =110 ;
L
3
:
3
x
= 100 · 0,2 + 150 · 0,8 =140 .
a) 2. Обчислимо сподівану корисність участі у лотереї за
формулою:
=⋅+⋅=⋅==
∑
=
22
2
1
11
)()()()())(( pxUpxUpxUхUxUM
i
ii
2
2
1
1
7
32
7
32
p
x
p
x
⋅
−
+⋅
−
= .
Для лотереї L
1
: +⋅
−
⋅
== 44,0
7
3362
)())((
11
xUxUM
66,1056,0
7
3412
=⋅
−⋅
+ .
Для лотереї L
2
: +⋅
−
⋅
== 8,0
7
81002
)())((
22
xUxUM
00,312,0
7
31502
=⋅
−⋅
+ .
Для лотереї L
3
: +⋅
−
⋅
== 2,0
7
31002
)())((
33
xUxUM
57,398,0
7
31502
=⋅
−⋅
+ .
Висновок. Оскільки суб’єкт керування повинен макси-
мізувати сподіване значення корисності результатів, то він
вибере лотерею L
3
, оскільки для неї сподіване значення
)())((
33
xUxUM = – максимальне.
3. Визначимо детермінований еквівалент
x
ˆ
(гарантовану
суму
x
ˆ
, отримання якої еквівалентне участі у лотереї) лотереї
L
1
за формулою:

307
U( x
ˆ
) = M(U(x)).
Для лотереї L
1
:
7
3
ˆ
2
1
−x
= 10,657, звідки
x
ˆ
1
=
2
37657,10
+
⋅
= 38,7995 = 38,8.
Для лотереї L
2
:
7
3
ˆ
2
2
−x
= 31,00, звідки
2
ˆ
x
=
=
2
3700,31 +⋅
= 110.
Для лотереї L
3
:
7
3
ˆ
2
3
−
x
= 39,5715, звідки
3
ˆ
x
=
=
=
+⋅
2
375715,39
= 140.
4. Обчислимо премію
π
за ризик участі у лотереї за фор-
мулою:
π
= xx
ˆ
− .
Для лотереї L
1
:
π
1
= 38,8 – 38,8 = 0.
Для лотереї L
2
:
π
2
= 110 – 110 = 0.
Для лотереї L
3
:
π
3
= 140 – 140 = 0.
Висновок. Зростаюча лінійна функція корисності харак-
теризує особу нейтральну до ризику, премія за ризик для якої
дорівнює нулю. Слід вибрати лотерею L
3
, оскільки для неї
сподіване значення корисності виграшу максимальне.
б) U(x) = x
4
.
2.Обчислимо сподівану корисність участі у лотереї :
L
1
: )(
1
xU = U(36) p
1
+ U(41) p
2
= (36)
4
·0,44 + (41)
4
·0,56 =
= 2321457,2;
L
2
: )(
2
xU = U(100) p
1
+ U(150) p
2
= (100)
4
·0,8 + (150)
4
·0,2 =
= 181250000;
L
3
: )(
3
xU = U(100) p
1
+U(150) p
2
= (100)
4
·0,2 + (150)
4
·0,8 =
= 425000000.
3.Визначимо детермінований еквівалент
x
ˆ
для лотерей:
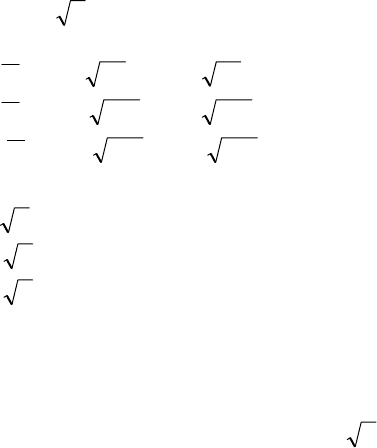
308
L
1
:
4
1
ˆ
x
= 2321457,2; звідки x
ˆ
=39,03;
L
2
:
4
2
ˆ
x
= 181250000; звідки x
ˆ
=116,03;
L
3
:
4
3
ˆ
x
= 425000000; звідки x
ˆ
=143,58.
4. Премія за ризик для лотерей складає:
L
1
:
π
1
= 38,8 – 39,03 = – 0,23;
L
2
:
π
2
= 110 – 116,03 = – 6,03;
L
3
:
π
3
= 140 – 143,58 = – 3,58.
Висновок. Функція корисності U(x) = x
4
, зростаюча і увіг-
нута вниз і оскільки
π
< 0, то вона характеризує особу
схильну до ризику. Треба вибрати лотерею L
3
, оскільки їй
відповідає найбільша сподівана корисність виграшу у лотереї.
в).U(x) =
4
х .
2. Обчислимо сподівану корисність участі у лотереї –
L
1
: )(
1
xU = 44,036
4
⋅ + 56,041
4
⋅ = 2,49;
L
2
: )(
2
xU =
8,0100
4
⋅
+
2,0150
4
⋅
= 3,23;
L
3
: )(
3
xU = 2,0100
4
⋅ + 8,0150
4
⋅ = 3,43.
3. Визначимо детермінований еквівалент
x
ˆ
для лотерей:
L
1
:
1
4
ˆ
x
= 2,4948; звідки x
ˆ
1
= (2,4948)
4
=38,74;
L
2
:
2
4
ˆ
x
= 3,2297; звідки x
ˆ
2
= (3,2297)
4
= 108,81;
L
3
:
3
4
ˆ
x
= 3,4322; звідки x
ˆ
3
= (3,4322)
4
= 138,77.
4. Премія за ризик
π
для участі у лотереях складає:
L
1
:
π
1
= 38,8 – 38,74 = 0,06;
L
2
:
π
2
=110 – 108,8086 = 1,19;
L
3
:
π
3
=140 – 138,7683 = 1,23.
Висновок. Функція корисності U(x)=
4
х зростаюча і
опукла вгору, і оскільки премія за ризик
π
> 0, то вона харак-
теризує особу несхильну до ризику. Оскільки лотереї L
3
від-
повідає найбільша сподівана корисність виграшу, то слід об-
рати лотерею L
3
.
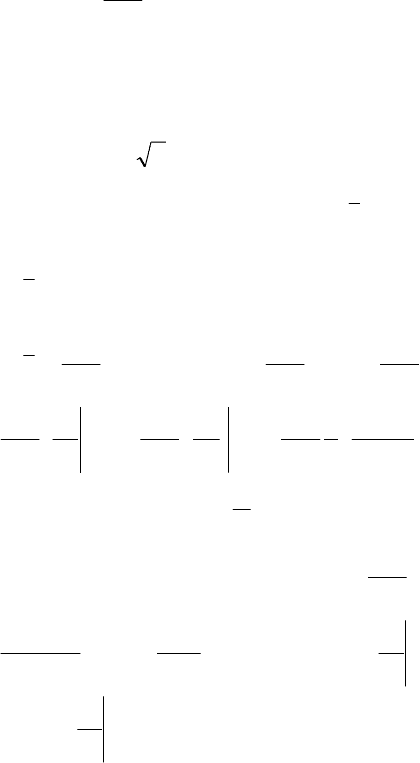
309
4.3.16. Знайти сподіваний виграш, детермінований еквіва-
лент та премію за ризик для лотереї, яка визначається такою
щільністю розподілу ймовірностей виграшу:
⎪
⎩
⎪
⎨
⎧
><
≤≤−⋅
=
.24,0,0
,240),24(
288
1
)(
xx
хx
xf
Корисність лотереї задається виразом:
а) U(x) = 0,890x;
б) U(x) = 0,5x
2
;
в) U(x) = 0,9
x .
Розв’язок
1.Обчислимо сподіваний виграш
x
у лотереї за форму-
лою:
dxxfхХМx
b
a
)()( ⋅==
∫
.
x
=
=−=−⋅
∫∫∫
24
0
24
0
2
24
0
288
1
288
24
)24(
288
1
dxxxdxdxxx
2288
24
2
x
⋅=
0
24
3288
1
3
х
⋅−
96
24
0
24
2
=
3288
241
2
⋅
⋅
= 24 – 16 = 8.
2. a). U(x) = 0,89x.
Сподівана корисність
)(xU рівна:
[]
=−⋅==
∫∫
24
0
24
0
)24(
288
1
89,0)()()( dxxxdxxfxUxUM
−=−
⋅
=
∫∫
24
0
2
24
0
2
24
0
2
0,074167
288
89,0
288
2489,0 x
dxxxdx
.122,7239,1436,21
3
00309,0
24
0
3
=−=−
x
Детермінований еквівалент знаходимо з формули :
U(
x
ˆ
) = M[U(x)]; 0,89 x
ˆ
= 7,121, звідки x
ˆ
= 8,001.
310
Премія за ризик складає:
π
=
x
– x
ˆ
= 8 – 8= 0.
Премія за ризик дорівнює 0, отже особа байдужа до
ризику.
б). U(x) = 0,5x
2
.
Сподівана корисність
)(xU рівна :
[]
∫∫
−⋅=−⋅=
24
0
2
24
0
2
288
24
5,0)24(
288
1
5,0)( dxxdxxxxUM
48144192
4
001736,0041667,0
288
5,0
24
0
4
24
0
24
0
3
3
=−=−=−
∫
x
x
x
dxx
.
Детермінований еквівалент складає:
0,5
x
ˆ
2
= 48; звідки x
ˆ
2
= 96 або x
ˆ
= 9,798;
Премія за ризик:
π
=
x
– x
ˆ
= 8 – 9,8 = – 1,8, премія менша 0, тому особа
схильна до ризику.
в). U(x) = 0,9
х .
Сподівана корисність )(xU рівна:
[]
∫∫
−⋅=−⋅=
24
0
24
0
288
24
9,0)24(
288
1
9,0)( dxxdxxxxUM
=−=
⋅
⋅
−
⋅
⋅
=−
∫
800
24
24
20
1
3320
21
3320
224
288
9,0
5
3
24
0
2
5
24
0
2
3
24
0
2
3
xx
dxx
= 5,87878 – 3,5273 = 2,352.
Детермінований еквівалент складає:
0,9
x
ˆ
=2,352 або x
ˆ
= 2,613, звідки x
ˆ
= 6,829.
Премія за ризик рівна:
π
=
x
– x
ˆ
= 8-6,82667 = 1,1733 > 0,
отже особа несхильна до ризику.
