Кармелюк Г.І. Теорія ймовірностей та математична статистика
Подождите немного. Документ загружается.


281
Задачі
4.3.1. Величина X має щільність розподілу f(х). f(x) –
парна функція.
Обчислити її математичне сподівання.
Розв’язок.
Математичне сподівання неперервної випадкової величи-
ни рівне
0)()( =⋅=
∫
∞
∞−
dxxfxXM , оскільки )(xf – парна
функція, то
)(xfx ⋅ – є непарною функцією, а інтеграл від
непарної функції з симетричними межами рівний 0.
4.3.2. Студент пам’ятає, що щільність показникового роз-
поділу має вигляд
x
eCxf
λ
−
⋅=)( при 0≥x , але він забув, чо-
му рівна постійна C. Потрібно знайти C.
Розв’язок.
Використаємо властивість щільності розподілу:
1)( =
∫
∞
∞−
dxxf
або
1
00
==
−
∞
−
∞
∫∫
dxecdxce
xx
λλ
, звідки
*
1
0
==
−
∞
∫
dxe
c
x
λ
==−=−−=
∞
−
∞
−−
∞
−
∞
∫∫
0
0
00
11
)(
1
xxxx
eexdedxe
λλλλ
λλ
λ
λ
()
.
1
01
111
0
λλλ
λ
λ
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=
∞
⋅−
e
e
.
1
1
*
λ
λ
==
Отже,
λ
=c .

282
4.3.3. Випадкова величина Х при
0≥x
задана щільністю
ймовірності (розподіл Вейбулла):
0
1
0
)(
x
x
n
n
ex
x
n
xf
−
−
⋅= .
Знайти моду Х.
Розв’язок.
Мода – це значення випадкової величини Х, при якому
диференціальна функція щільності f(x) має максимум.
Для цього обчислимо першу похідну по х і прирівняємо її
до 0.
0)1()(
0
1
12
0
00
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−=
−
−
−
−
−
x
nx
exexn
x
n
xf
n
x
x
n
x
x
nI
nn
.
Винесемо за дужки
2
0
−
−
n
x
x
xe
n
, отримаємо:
×
−
−
2
0
0
n
x
x
xe
x
n
n
.011
0
2
00
1
0
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅⋅
−−×
−
−
−
x
xn
nxe
x
n
x
nxx
n
n
n
x
x
n
n
Отже,
n
x
n
xn
=
−
0
)1(
або
n
x
n
n
x
1
0
1
⎥
⎦
⎤
⎢
⎣
⎡
−
=
. Таким чином,
n
x
n
n
xMo
1
0
1
)(
⎥
⎦
⎤
⎢
⎣
⎡
−
=
.
4.3.4. Випадкова величина Х в інтервалі (0; 1) задана
щільністю розподілу f(x) = 2x; поза цим інтервалом f(x) = 0.
Знайти початкові і центральні моменти 1, 2, 3 і 4
порядків.
Розв’язок.
Початкові моменти знайдемо згідно формули:

283
dxxfxv
b
a
k
k
)(⋅=
∫
. Отже,
3
2
1
3
2
3
222
1
0
3
2
1
0
1
0
1
=⋅===⋅=
∫∫
x
dxxxdxxv
;
2
1
4
222
1
0
4
3
1
0
2
1
0
2
===⋅=
∫∫
x
dxxxdxxv
;
5
2
5
222
1
0
5
4
1
0
3
1
0
3
===⋅=
∫∫
x
dxxxdxxv
;
3
1
6
2
22
1
0
65
1
0
4
1
0
4
===⋅=
∫∫
xdxxxdxxv
.
Центральні моменти обчислимо через початкові:
0
1
=
μ
;
18
1
9
4
2
1
3
2
2
1
2
2
122
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
vv
μ
;
+−=
⎟
⎠
⎞
⎜
⎝
⎛
⋅+⋅⋅−=+−= 1
5
2
3
2
2
2
1
3
2
3
5
2
23
3
3
12133
vvvv
μ
135
1
135
1358054
27
16
−=
−+
=+
;
−⋅
⎟
⎠
⎞
⎜
⎝
⎛
+⋅⋅−=−+−=
2
1
3
2
6
5
2
3
2
4
3
1
364
2
4
12
2
13144
vvvvvv
μ
.
135
1
953
8018014445
27
16
3
4
15
16
3
1
3
2
3
4
=
⋅⋅
−+−
=−+−=
⎟
⎠
⎞
⎜
⎝
⎛
⋅−
284
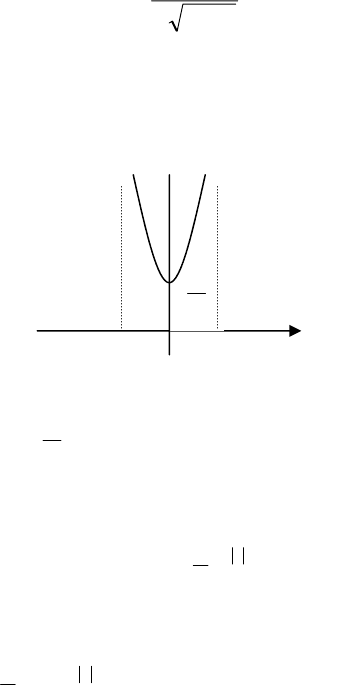
4.3.5. Випадкова величина Х в інтервалі (-1; 1) задана
щільністю розподілу
2
1
1
)(
x
xf
−
=
π
; поза цим інтервалом
f(x) = 0.
Знайти моду та медіану Х.
Розв’язок.
а) Моди Х нема (щільність розподілу не має максимуму).
б) М(Х) = 0 (крива розподілу симетрична відносно х = 0);
Рис. 4.3.1.
;.
1
)(;0
π
== xfx
∞
→
±→
)(lim
1
xf
x
(див. рис. 4.3.1).
4.3.6. Випадкова величина Х задана щільністю ймовір-
ності (розподіл Лапласа)
x
exf
−
=
2
1
)( . Знайти математичне
сподівання величини Х.
Розв’язок.
0
2
1
)( ==
−
∞
∞−
∫
dxxeXM
x
, як інтеграл від непарної функ-
ції з симетричними межами.
π
1
Х
1
-1
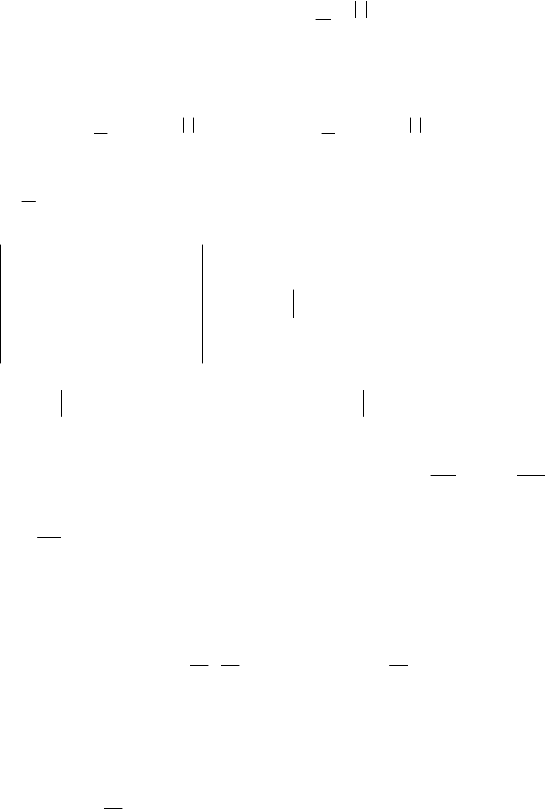
285
4.3.7. Випадкова величина Х задана щільністю ймовір-
ності (розподіл Лапласа)
x
exf
−
=
2
1
)( . Знайти дисперсію
величини Х.
Розв’язок.
=⋅=−⋅=
−
∞
∞−
−
∞
∞−
∫∫
dxexXMdxexXD
xx
222
2
1
)(
2
1
)(
N
==−=−−=⋅=
−
∞
−
∞
−
∞
−
∞
∫∫∫∫
)()()(
2
1
2
2
0
2
0
2
0
2
0
x
dv
x
u
xx
edxedxxdexdxex
N
==−⋅=
−⋅=
==
==
=
−
∞
−
∞
∞
−−−
∫∫
∫∫
dv
x
u
xxxx
edxdxxeex
vduvuudv
eveddv
xdxduux
)(22;);(
;2;
00
0
2
2
.2lim222)(22
0
0
00
0
=⋅−==−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
−
∞→
∞
−−
∞
−
∞
∞
−
∫∫
x
x
xxxx
eeexdedxexe
Тут враховано, що
===
∞→∞→
−
∞→
x
x
x
x
x
x
e
x
e
x
ex
2
limlimlim
2
2
;0
2
lim ==
∞→
x
x
e
.0lim =
−
∞→
x
x
xe
4.3.8. Щільність розподілу неперервної випадкової вели-
чини Х в інтервалі
⎟
⎠
⎞
⎜
⎝
⎛
−
2
;
2
ππ
рівна
xxf
2
cos
2
)(
π
=
; поза цим
інтервалом f(x) = 0.
Знайти ймовірність того, що в трьох незалежних
випробуваннях Х двічі прийме значення, яке належить
інтервалу
⎟
⎠
⎞
⎜
⎝
⎛
4
;0
π
.
286
Розв’язок.
⎪
⎪
⎩
⎪
⎪
⎨
⎧
= xxf
2
cos
,0
2
)(
π
,
⎟
⎠
⎞
⎜
⎝
⎛
−∈
2
;
2
ππ
x ;
Імовірність того, що задана випадкова величина Х знахо-
диться в заданому інтервалі, рівна:
===
⎟
⎠
⎞
⎜
⎝
⎛
≤≤
∫∫
xdxdxxfXP
2
4
0
4
0
cos
2
)(
4
0
π
π
ππ
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
===
∫∫
dx
xx
xxdx
2
2cos12
2
2cos1
coscos
2
4
0
22
4
0
ππ
ππ
=
⋅
+=
⋅
+
⋅
=
∫∫
4
0
4
0
4
0
4
0
2sin
2
11
2cos
2
2
2
2
ππ
ππ
ππππ
xxxdxdx
()
.
4
2
2
1
4
1
01
2
1
4
1
0sin
2
sin
2
1
4
1
π
π
ππ
π
π
π
π
+
=+=−+=
⎟
⎠
⎞
⎜
⎝
⎛
−+⋅=
Тоді імовірність описаної події А знайдемо за формулою
Бернуллі:
knkk
n
k
n
qpCAP
−
=)( , де ,
4
0
⎟
⎠
⎞
⎜
⎝
⎛
≤≤=
π
Xpp pq −
=
1 ,
π
π
π
π
π
π
π
4
23
4
24
4
2
11
−
=
−
−
=
+
−=−= pq .
Отже,
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+
=
−232
2
33
4
23
4
2
)2(
π
π
π
π
CP
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅=
π
π
π
π
4
23
4
2
3
2
.
поза інтервалом.
287
4.3.9. Щільність розподілу неперервної випадкової вели-
чини Х в інтервалі (0; 1) рівна f(x) = Carctgx; поза цим інтер-
валом f(x) = 0.
Знайти постійний параметр C.
Розв’язок.
Шуканий параметр С знайдемо з рівності:
;1)( =
∫
dxxf
b
a
або
;1
1
0
=
∫
Сarctgxdx
звідки
.
1
1
0
arctgxdx
С
∫
=
Обчислимо знаменник:
=
∫
arctgxdx
1
0
=
+
⋅−⋅=
−⋅=
==
+
==
=
∫
∫∫
2
1
0
1
0
2
1
;;
;
1
;
x
dx
xarctgxx
udvvuudv
xvdvdx
x
dx
duuarctgx
=+−=
+
+
−−⋅=
∫
1
0
2
2
2
1
0
)1ln(
2
1
41
)1(
2
1
011 x
x
xd
arctg
π
.
4
4ln
4
2ln2
2ln
2
1
4
1ln
2
1
2ln
2
1
4
−
=
−
=−=+−=
π
π
π
π
Отже,
.
4ln
4
4
4ln
1
−
=
−
=
π
π
C
4.3.10. Випадкова величина Х в інтервалі (-3; 3) задана
щільністю розподілу
2
9
1
)(
x
xf
−
=
π
; поза цим інтервалом
f(x) = 0.
а) Знайти моду та медіану Х.
б) знайти дисперсію Х;
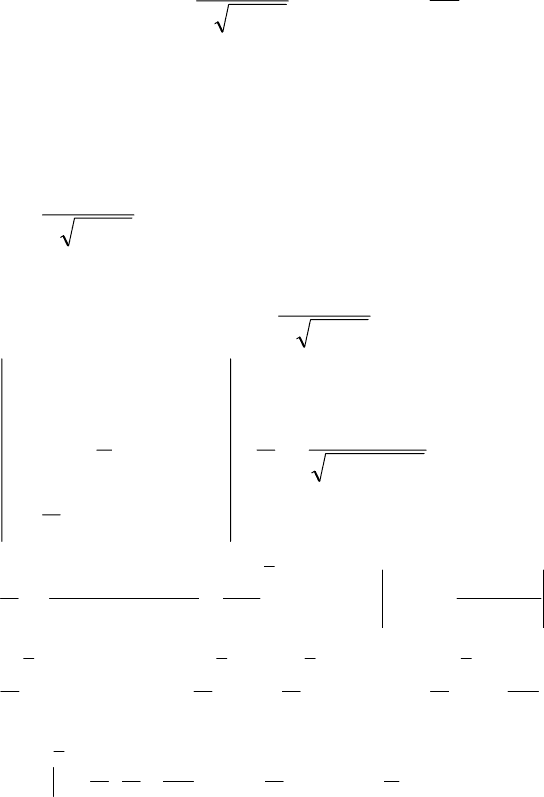
288
в) що імовірніше: в результаті випробування виявиться
Х < 1 чи Х > 1?
Розв’язок.
а)
;
9
1
lim)(lim
2
33
∞→
−
=
±→±→
х
xf
xx
π
(min).
3
1
)0(
π
=f
Функція існує при
)33(
<
<
−
X .
Функція щільності немає максимуму, тому моди теж не-
має.
Крива щільності симетрична відносно прямої х = 0, тому
Ме = 0, М(Х) = 0. Останнє випливає з формули:
=)(XM
0
9
1
2
3
3
=
−
=
∫
−
dx
х
x
π
як інтеграл від непарної підінтеграль-
ної функції з симетричними межами.
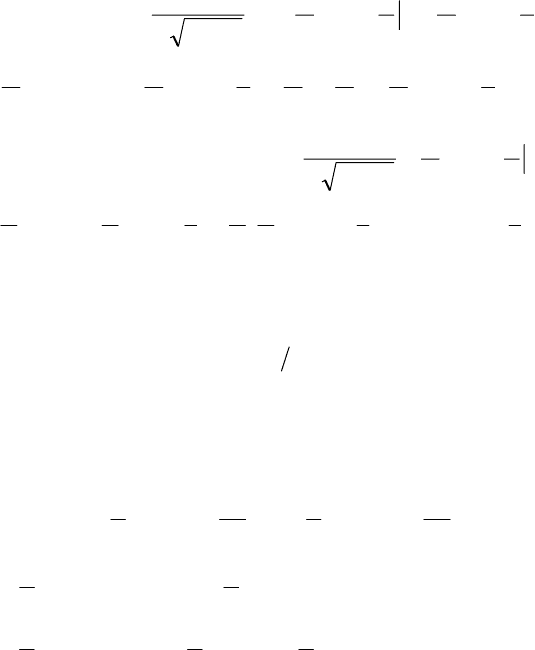
б) Дисперсія
=
−
=
∫
−
dx
х
xXD
2
2
3
3
9
1
)(
π
=⋅
−
=
==
=
==
=
∫
−
tdt
t
t
tt
x
t
tdtdxtx
cos3
sin99
sin91
0;
2
;
3
arcsin
;cos3;sin3
2
2
3
3
21
π
π
=
−
==
⋅
=
⋅
=
∫∫
2
2cos1
sinsin
92
cos3
cos3sin92
22
2
0
2
3
0
t
ttdt
t
tdtt
π
ππ
×−=−=−=
∫∫∫∫
πππππ
ππππ
2
99
2cos
99
)2cos1(
9
2
0
2
0
2
0
2
0
ttdtdtdtt
.5,4
2
9
0sin
2
2sin
2
9
2
9
2sin
2
0
==
⎟
⎠
⎞
⎜
⎝
⎛
−⋅−⋅=×
π
π
π
π
π
t
289
в) Обчислимо імовірність
=
<
<
−
=
<
)13()1( XPXP
−==
−
==
−
−−
∫∫
3
1
arcsin
1
3
arcsin
1
9
1
)(
1
3
2
1
3
1
3
ππ
π
x
dx
х
dxxf
.5,0
3
1
arcsin
1
2
1
3
1
arcsin
1
)1arcsin(
1
+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
−−
⎟
⎠
⎞
⎜
⎝
⎛
=−−
π
π
πππ
==
−
=<<=>
∫
3
1
2
3
1
3
arcsin
1
9
1
)31()1(
x
х
XPXP
π
π
.
3
1
arcsin5,0
3
1
arcsin
2
1
3
1
arcsin
1
1arcsin
1
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
⎟
⎠
⎞
⎜
⎝
⎛
−=
π
πππ
Отже,
)1()1( >>< XPXP .
4.3.11. Випадкова величина Х в інтервалі (3; 5) задана щі-
льністю розподілу
4/456)43()(
2
−+−= xxxf , поза цим
інтервалом
0)( =xf . Знайти моду, математичне сподівання і
медіану Х.
Розв’язок.
Виділимо в функції щільності повний квадрат:
=
⎥
⎦
⎤
⎢
⎣
⎡
+−
⎟
⎠
⎞
⎜
⎝
⎛
−=−+−=
4
45
6
4
3
4
45
6
4
3
)(
22
xxxxxf
[]
[
]
=−+⋅−−=+⋅−−= 11642
4
3
1542
4
3
22
xxxx
()
[]
()
.
4
3
4
4
3
14
4
3
22
+−−=−−−= xx
Як видно з цього виразу, при х = 4 щільність розподілу
досягає максимуму; отже, Мо(Х) = 4. Оскільки крива розпо-
ділу симетрична відносно х = 4, то М(Х) = 4, Ме(Х) = 4:
М(Х) = Мо(Х) = Ме(Х) = 4.
4.3.12. Величина X має щільність розподілу f(х).
Обчислити її математичне сподівання:
290
⎩
⎨
⎧
−−
=
0
11
)(
x
xf
Розв’язок.
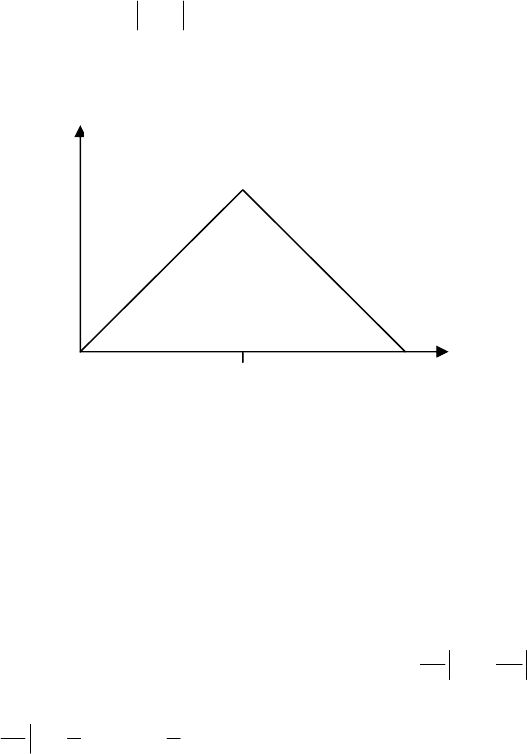
Графік функції щільності поданий на рис 4.3.2.
Рис. 4.3.2.
Розіб’єм інтервал х є [0;2] на два інтервали [0;1] і [1;2],
так що:
=⋅+⋅=⋅=
∫∫∫
dxxfxdxxfxdxxfxXM )()()()(
2
1
1
0
2
0
+⋅=−−+−−=
∫∫∫
xdxxdxxxdxxx
1
0
2
1
1
0
)]1(1[)]1(1[
−+=−+=−+
∫∫∫∫
2
1
2
1
0
3
2
2
1
2
1
2
1
0
2
1
2
2
3
2)2(
xx
dxxxdxdxxxdxx
.1)18(
3
1
14
3
1
3
2
1
3
=−−−+=−
x
Отже, М(Х) = 1, що й видно з малюнка.
4.3.13. Випадкова величина X має щільність ймовіpності:
, якщо х
∈
[0; 2],
, якщо x > 2.
f(
х
X
0
1
2
