Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


331
Розділ IV. Диференційне числення функції однієї змінної
VІІІ. Побудуємо графік.
3)
3
23
6
y
xx
.
І. Функція визначена для будь+якого
х
, тобто
х
(
f
,
f
).
ІІ. Функція неперервна на всій осі.
ІІІ. Дослідимо функцію на парність чи непарність:
у
(
х
)
=
23
3
6
x
x
;
у
(–
х
)
=
23
3
6( ) ( )
x
x
=
23
3
6
x
x
,
f
(
x
)
z
f
(–
x
);
f
(
x
)
z
–f
(–
x
).
Отже, функція є ані парною, ані непарною. Функція неперіодична.
ІV. Знаходимо точки перетину з осями координат:
а) з віссю
Ох
:
3
23
0
6
y
y
xx
°
®
°
¯
3
23
0
60
y
xx
°
®
°
¯
23
0
60
y
xx
®
¯
2
0
(6 ) 0
y
xx
®
¯
12
0
0, 6
y
xx
®
¯
;
б) з віссю
Оу
:
3
23
0
6
x
y
xx
°
®
°
¯
3
23
0
60
x
xx
°
®
°
¯
0
0
x
y
®
¯
Тому (0; 0)
і
(6; 0) — точки перетину графіка з віссю
Ох
; (0; 0) —
точка перетину графіка з віссю
Оу
.
V. Визначимо асимптоти кривої:
Вертикальних асимптот немає.
Похилі:
у = kx + b
.
k =
lim
x
orf
()
f
x
x
=
lim
x
orf
3
23
6xx
x
=
lim
x
orf
23
3
3
6xx
x
=
=
lim
x
orf
3
6
1
x
=
–1;

332
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
b =
lim
xorf
(
f
(
x
)
– kx
)
=
lim
xorf
(
23
3
6xx
+ х
)
=
=
lim
x
orf
23 232 23 2
33
3
232 23 2
3
3
(6 )((6 ) 6 )
(6 ) 6
x
xx xx xxxx
xx xxxx
=
=
lim
x
orf
233
3
232 23 2
3
6
(6 ) 6
xxx
xx xxxx
=
=
lim
x
orf
2
2
3
232 23 2
3
622
6
(6 ) 6
x
x
xx xxx x
xxx
=
=
lim
x
orf
456 23
33
633
6
36 12 6
1
xxx xx
xxx
=
6
3
=
2
.
Отже,
у = –х +
2 — похила асимптота.
VІ. Знаходимо
y
c
і визначаємо критичні точки:
y
c
=
1
23
3
(6 ) )xx
c
=
2
232
3
12 3
3(6 )
xx
xx
=
2
232
3
4
(6 )
xx
xx
.
1) Із рівняння
y
c
= 0:
2
232
3
4
(6 )
xx
xx
=
0,
4
х – х
2
=
0,
х
(4
– х
)
= 0,
х
1
= 0,
х
2
= 4.
2)
y
c
=
f
,
6
х
2
– х
3
=
0,
х
2
(6
– х
)
=
0,
х
3
= 6.
х
1
= 0,
х
2
= 4,
х
3
= 6
—
критичні точки.
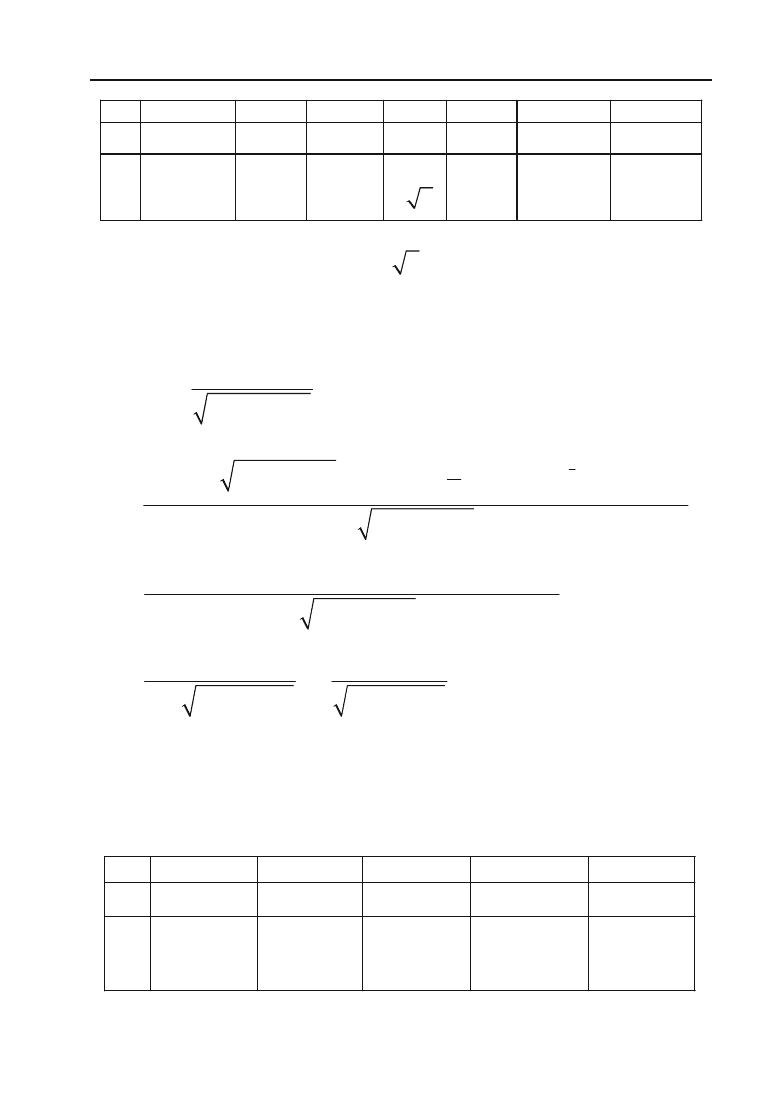
Розбиваємо область визначення критичними точками на інтер+
вали і за знаком похідної в цих інтервалах встановлюємо інтервали
монотонності та екстремуми:
333
Розділ IV. Диференційне числення функції однієї змінної
Отже,
у
min
(0) = 0,
у
max
(4)
=
3
24
.
VІІ. Знайдемо точки перегину та інтервали опуклості та вгнутості
кривої:
y
cc
=
2
232
3
4
(6 )
xx
xx
c
§·
¨¸
¨¸
©¹
=
=
1
3
232 2 2 3 2
3
234
3
2
(4 2 ) (6 ) (4 ) (6 ) (12 3 )
3
(6 )
xxx xx xx xx
xx
=
=
23 2 2
235
3
3(4 2 )(6 ) 2(4 )(12 3 )
3(6 )
xxx xx xx
xx
=
=
2
24 5
3
24
3(6)
x
xx x
=
45
3
8
(6 )xx
.
y
cc
z
0,
y
cc
=
f
,
х
4
(6
– х
)
5
= 0,
х
1
= 0;
х
2
= 6 — критичні точки другого роду.
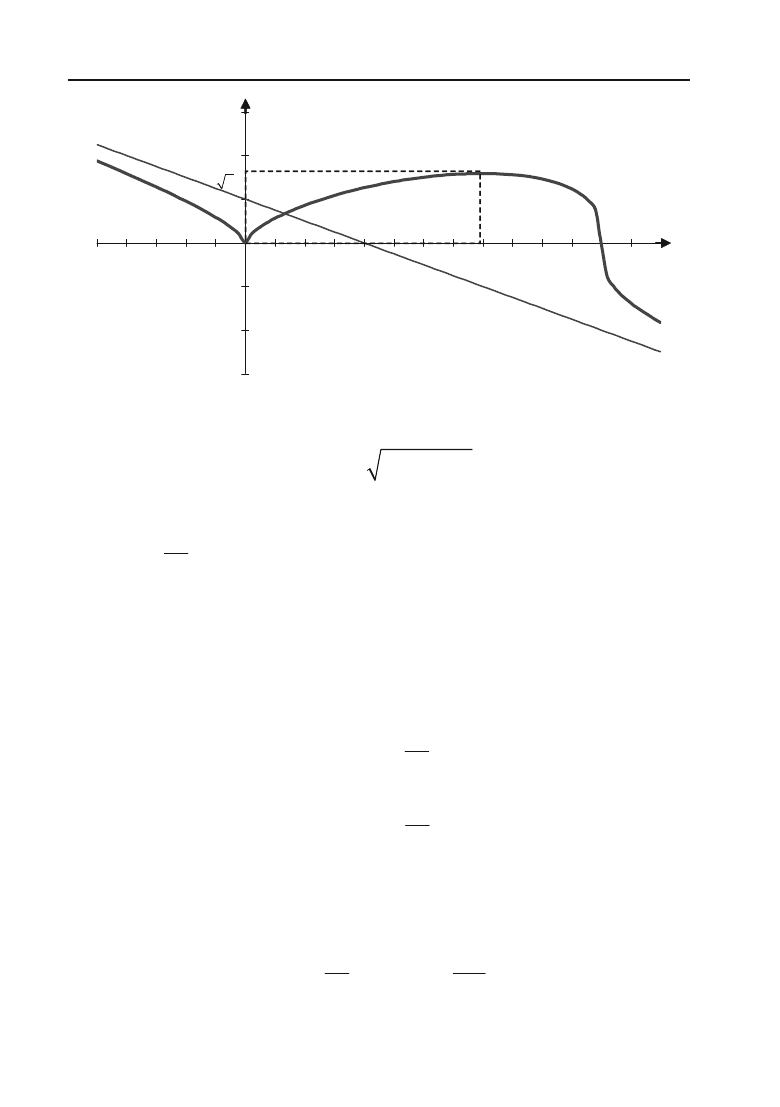
Складаємо таблицю і досліджуємо знак
y
cc
поблизу кожної кри+
тичної точки другого роду.
х (
f
;0) 0 (0; 4) 4 (4; 6) 6 (6;
f
)
y
c
–
f
+ 0 –
f
–
у
2
mіn 0
/
max
3
24
2
немає
екстре+
муму
2
х (
f
; 0) 0 (0; 6) 6 (6;
f
)
y
c
–
f
–
f
+
у
крива
опукла
перегину
немає
крива
опукла
0
точка
перегину
крива
вгнута
334
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
у
пер
(
х = 6
)
=
23
3
6(6) 6
=
0.
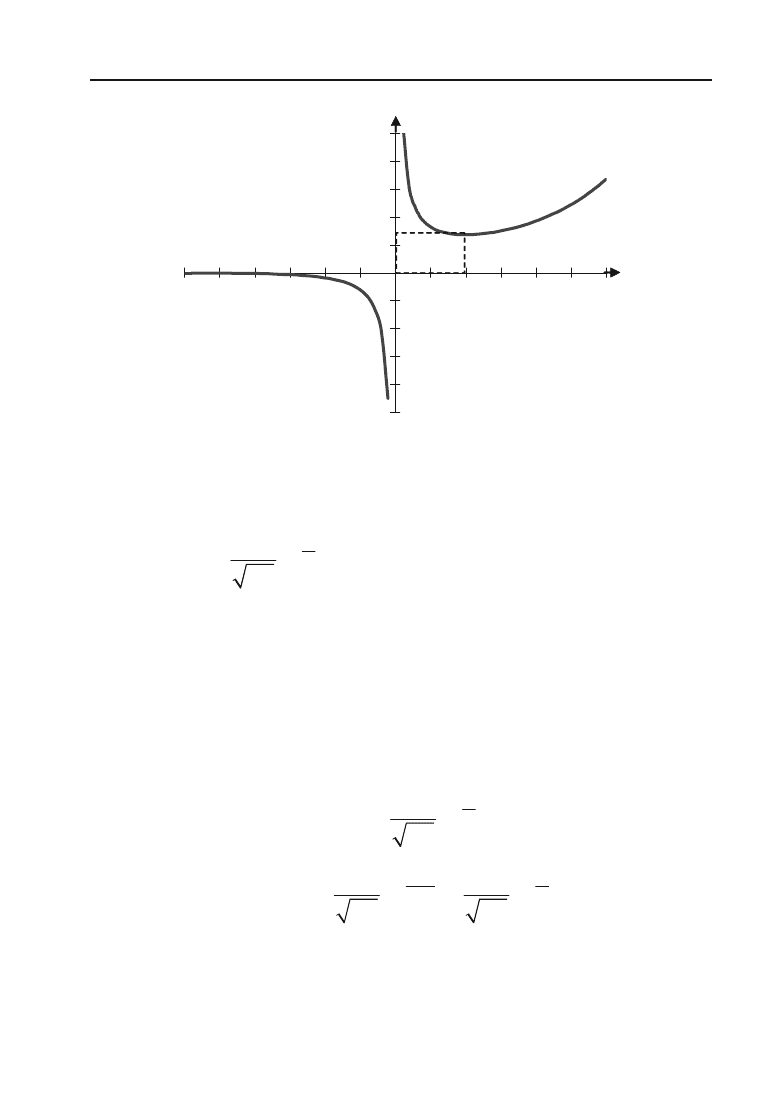
VІІ. Побудуємо графік:
4)
x
e
y
x
.
І. Функція визначена для будь+якого
х,
крім
х
= 0, тобто в інтер+
валах (
f
, 0) і (0;
f
).
ІІ. Знайдемо точки розриву та її односторонні границі в точках
розриву:
х =
0.
00
lim
x
y
o
=
00
lim
x
o
x
e
x
=
f
,
00
lim
x
y
o
=
00
lim
x
o
x
e
x
=
f
.
Функція неперервна в інтервалах (
f
, 0) і (0;
f
). Функція
неперіодична.
ІІІ. З’ясуємо чи є функція парною чи непарною:
f
(
x
)
=
x
e
x
, f
(
–x
)
=
x
e
x
.
+6
+4
+2
0
2
4
6
+2,5 +2 +1,5 +1 +0,5 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 5,5 6 6,5 7
X
Y
3
24
у = 2 – х
Рис. 4.16.
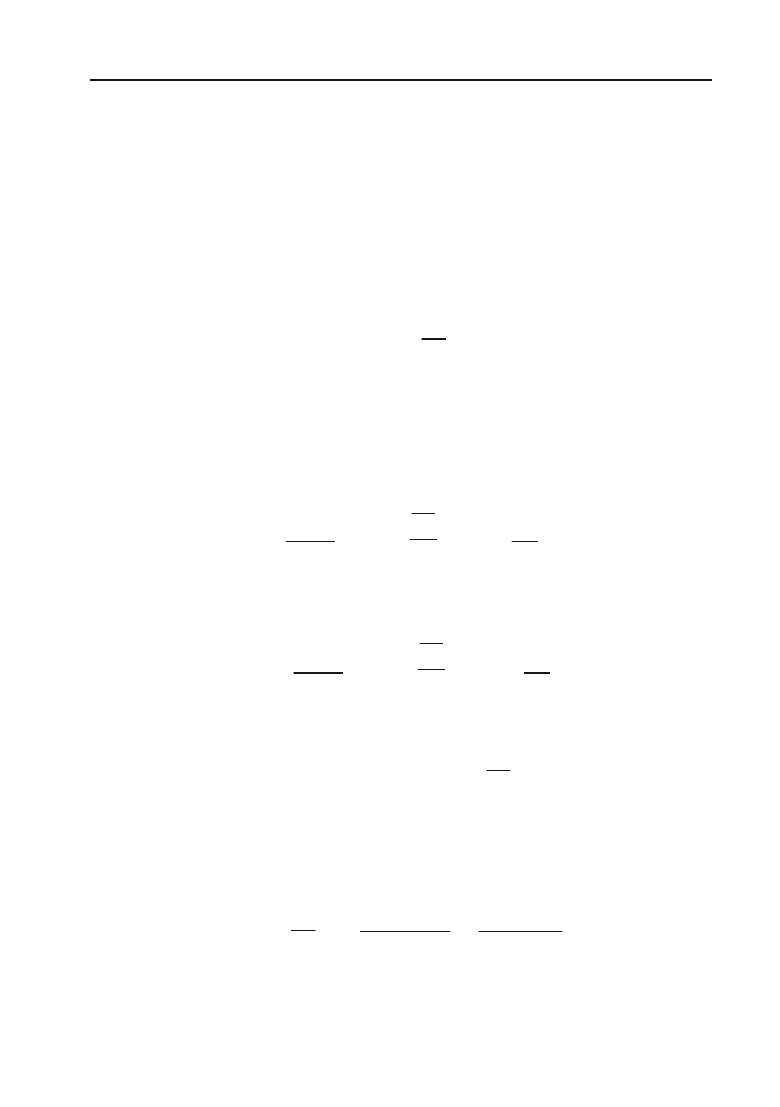
335
Розділ IV. Диференційне числення функції однієї змінної
Ні одна із нерівностей
f
(
x
)
z
f
(
–x
),
f
(
x
)
z
–f
(
–x
)
не має місце.
Отже, функція ані парна, ані непарна.
ІV. Графік функції не перетинає осей координат, так як
х
z
0
і
у
z
0.
V. Визначемо асимптоти графіка функцій:
а) Значення
х =
0 (тобто вся вісь
Оу
) являється вертикальною
асимптотою кривої.
б) Горизонтальні асимптоти:
lim
x
y
of
=
lim
x
of
x
e
x
=
f
,
lim
x
y
of
=
lim
xof
=
0
.
Горизонтальною асимптотою являється вісь
Ох
(
у =
0).
в) Знайдемо похилі асимптоти, рівняння яких
у = kx + b
.
k
1
=
lim
xof
()fx
x
=
lim
x
of
x
e
x
x
=
lim
x
of
2
x
e
x
=
f
.
Це означає, що при
х
o
f
похилих асимптот немає.
k
2
=
lim
xof
()fx
x
=
lim
xof
x
e
x
x
=
lim
xof
2
x
e
x
= 0,
b =
lim
x
of
(
f
(
x
)
– kx
)
=
lim
x
of
x
e
x
=
0.
у
= 0
(похила асимптота співпадає з гризонтальною).
VІ. Визначемо точки екстремуму та інтервали зростання та спа+
дання функції.
y
c
=
x
e
x
c
§·
¨¸
©¹
=
2
x
x
exe
x
=
2
(1)
x
ex
x
.
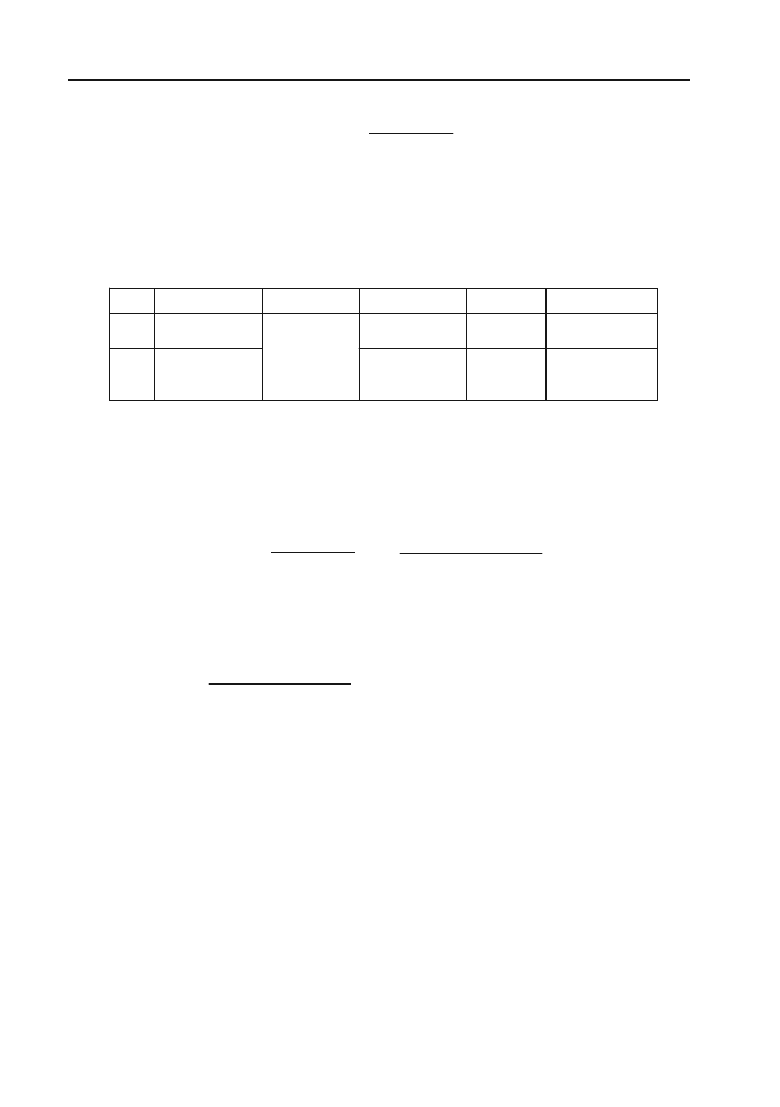
Знаходимо критичні точки:
336
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1) Із рівняння
y
c
= 0, тобто
2
(1)
x
ex
x
=
0, слідує, що
х =
1.
2)
y
c
=
f
при
х =
0, але при
х
= 0 функція не визначена. Таким
чином, функція має критичну точку
х
= 1. Область визначення
функції поділимо на інтервали (
f
; 0),(0; 1), (1;
f
).
Складемо таблицю:
Отже,
у
min
(1) =
е
,
VІІ. Знайдемо точки перегину та інтервали опуклості та вгнутості
кривої:
y
cc
=
2
(1)
x
ex
x
c
§·
¨¸
©¹
=
2
3
(22)
x
ex x
x
.
Знайдемо критичні точки другого роду.
З рівняння
2
3
(22)
x
ex x
x
=
0,
враховуючи, що
е
х
z
0, то
х
2
–
2
х
+
2 = 0, але дискріменент квадратного рівняння менший за нуль.
Отже, немає дійсних значень
х
, при яких друга похідна дорівнює 0.
Знайдемо значення
х,
при яких
y
cc
f
. Таким единим значенням
являється
х =
0. але точка перегибу при
х =
0 не може бути, так як
при
х =
0 задана функція не існує. Отже, точка перегибу графіка
функції не існує.
Для визначення інтервалів опуклості та вгнутості графіка функції
розглянемо знак
y
cc
на інтервалах (
f
, 0) і (0;
f
).
y
cc
< 0
на (
f
, 0), крива опукла;
y
cc
> 0
на (0;
f
), крива вгнута.
х (
f
; 0) 0 (0; 1) 1 (1;
f
)
y
c
– – 0 +
у
2
не
існує
2
mіn е
/
337
Розділ IV. Диференційне числення функції однієї змінної
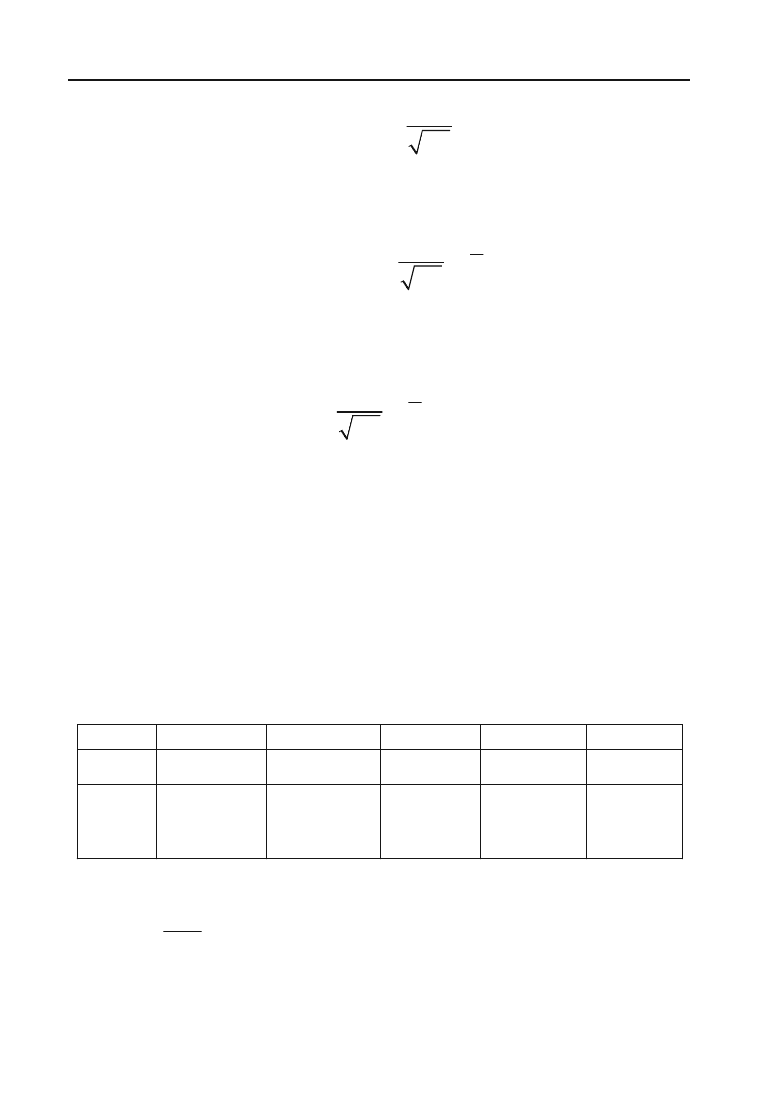
VІІІ. Побудуємо графік. Рис. 4.17.
5)
()
x
M
=
1
2
S
2
2
x
e
.
Функція, яка відіграє важливу роль в теорії ймовірностей, а та+
кож в математичній та економічній статистиці.
І. Функція визначена для будь+якого дійсного значення
х
. вона
приймає тільки додатні значення:
х
(
f
,
f
);
()
x
M
(0;
f
).
ІІ. Точок розриву немає. Функція неперервна на інтервалі
(
f
,
f
).
ІІІ. Функція парна:
()x
M
=
1
2
S
2
2
x
e
,
()x
M
=
1
2
S
2
()
2
x
e
=
1
2
S
2
2
x
e
,
так як
()x
M
=
()x
M
.
Графік функцій симетричний відносно осі ординат.
+10
+8
+6
+4
+2
0
2
4
6
8
10
+3 +2,5 +2 +1,5 +1 +0,5 0 0,5 1 1,5 2 2,5 3
X
Y
e
Рис. 4.17.
338
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
ІV. При
х =
0 значення
()x
M
=
1
2
S
|
0,4
.
Точок перетину з віссю
Ох
немає, так як
()x
M
z
0.
V. Знайдемо асимптоти:
lim
xorf
()x
M
=
lim
x
orf
1
2
S
2
2
x
e
=
0
.
Отже, вісь
Ох
(
у
= 0) є горизонтальною асимптотою кривої.
VІ. Знайдемо точки екстремуму та інтервали монотонності.
Знаходимо першу похідну функції:
()x
M
c
= –х
1
2
S
2
2
x
e
= –х
()x
M
.
Очевидно,
()
x
M
c
>
0 для
х <
0 і
()
x
M
c
<0 для
х>
0.
При
х =
0 функція досягає максимуму
max
M
=
(
0
)
M
|
0,4
.
VІІ. Знаходимо точки перегину та інтервали опуклості та вгну+
тості кривої.
Друга похідна функції має вигляд:
()
x
M
cc
= –
()x
M
– х
()
x
M
c
= –
()x
M
+ х
2
()x
M
=
()x
M
(
х
2
– 1)
.
Так як
()x
M
>
0, то знак
()
x
M
cc
залежить від знаку
х
2
– 1. Кри+
тичних точок буде дві. Це
х =
–1 і
х =
1.
Схема знаків другої похідної має вигляд:
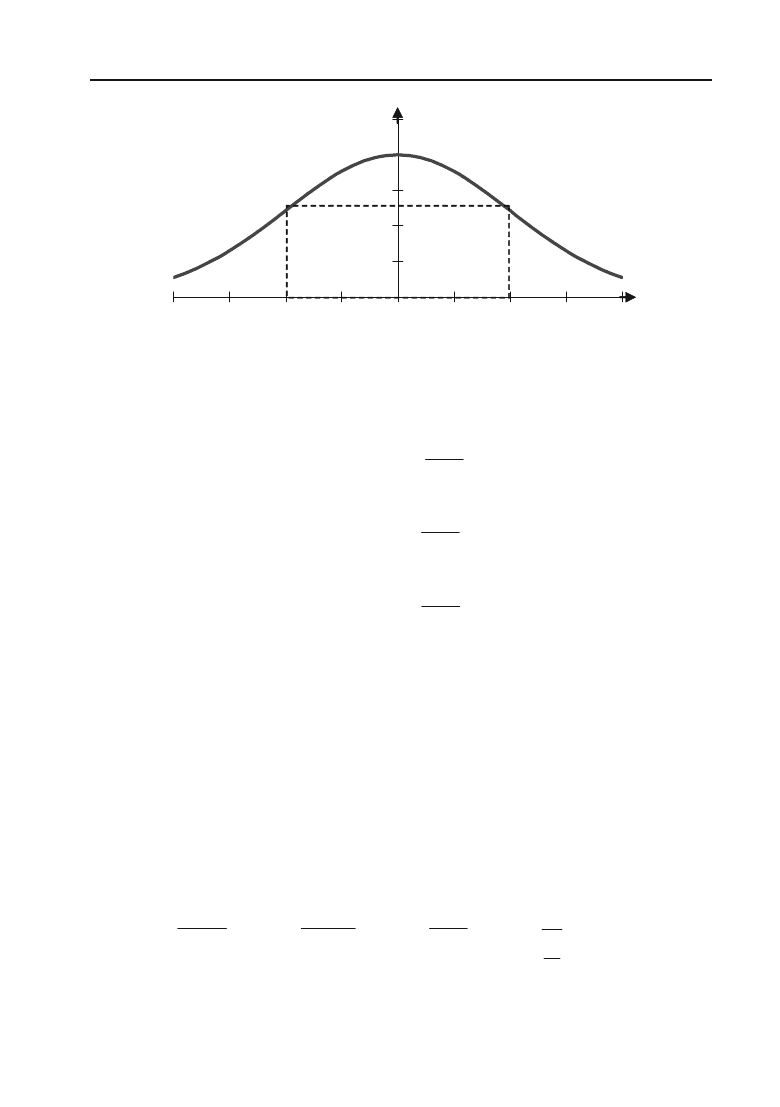
VІІІ. Побудуємо графік. Рис. 4.18.
6)
2
ln
x
y
x
.
І. Функція визначена в інтервалах
х
(0; 1)
(1;
f
).
ІІ. Точками розриву функції є точки
х
= 0 та
х =
1.
х (
f
; –1) –1 (–1; 1) 1 (1;
f
)
()x
M
cc
+ 0 – 0 +
()x
M
вгнута
точка
перегину
0,24
опукла
точка
перегину
0,24
вгнута
339
Розділ IV. Диференційне числення функції однієї змінної
Знаходимо односторонні границі в точках розриву:
00
lim
x
y
o
=
00
lim
x
o
2
ln
x
x
=
0
.
10
lim
x
y
o
=
10
lim
xo
2
ln
x
x
=
f
.
10
lim
x
y
o
=
10
lim
xo
2
ln
x
x
=
f
.
ІІІ. Функція не є ані парною ані непарною.
ІV. Знаходимо точки перетину графіка функції з осями коорди+
нат. З віссю
Оу
графік не перетинається, бо
х
z
0; з віссю
Ох
він та+
кож не перетинається.
V. Знаходимо асмптоти графіка функції. Оскільки
10
lim
x
y
o
=
f
,
10
lim
x
y
o
=
f
, то
х =
1 — вертикалльна асимптота. Зщнаходимо по+
хилі асимптоти:
у = kx + b.
Маємо
k =
lim
xof
()fx
x
=
lim
xof
2
ln
x
x
x
=
lim
x
of
ln
x
x
=
lim
xof
1
1
x
=
lim
x
of
х =
f
.
Отже, похилих асимптот немає.
0
0,1
0,2
0,3
0,4
0,5
+2 +1,5 +1 +0,5 0 0,5 1 1,5 2
X
Y
0,24
Рис. 4.18.
340
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
VІ. Знаходимо точки екстремуму та інтервали монотонності
функції:
y
c
=
2
2
1
2ln
(ln )
xxx
x
x
=
2
2ln
(ln )
x
xx
x
=
2
(2ln 1)
(ln )
xx
x
;
y
c
=
0,
х
(2ln
x
– 1) = 0.
Враховуючи область визначення функції:
х
z
0, 2ln
x
– 1 = 0, ln
x =
1
2
, x =
1
2
e
=
e
.
Подальший розв’язок можна оформити у вигляді таблиці:
VІІ. Знаходимо вгнутості і опуклості та точки перегину графіка
функції:
y
cc
=
2
4
11
(2ln 1 2 )(ln ) (2 ln )2ln
(ln )
xxxxxxx
xx
x
=
=
4
ln
((
2ln 1
)
ln 4 ln 2
)
(ln )
xx xxxx
x
=
2
4
ln (2ln 3ln 2 )
ln
xxxx
x
.
Точок перегину немає, бо
y
cc
не обертається в нуль ні за якого
значення
х
.
y
cc
>
0 при
х
(0; 1),
графік функції вгнутий;
y
cc
<
0 при
х
(1;
f
),
графік функції опуклий.
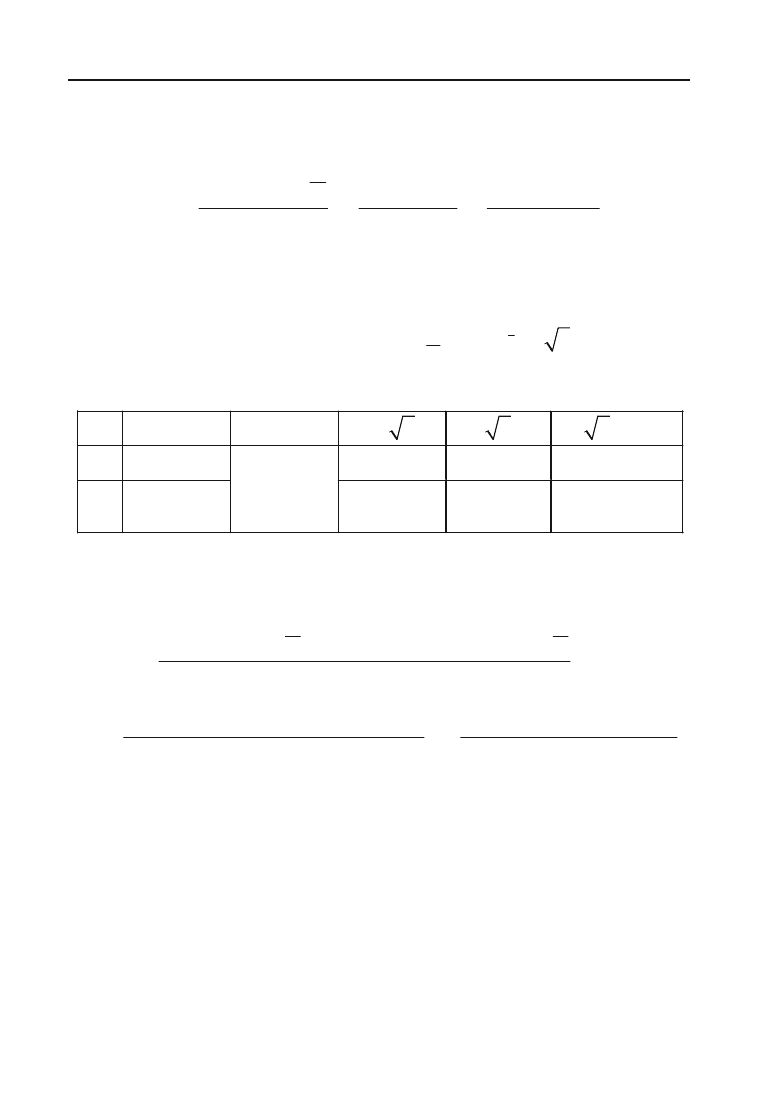
VІІІ. Будуємо графік функції з урахуванням того, що
у
o
0 при
х
o
0. Рис. 4.19.
х (0; 1) 1
(1;
e
)
e
(
e
;
f
)
y
c
– – 0 +
у
2
не
існує
2
mіn 2е
/
