Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

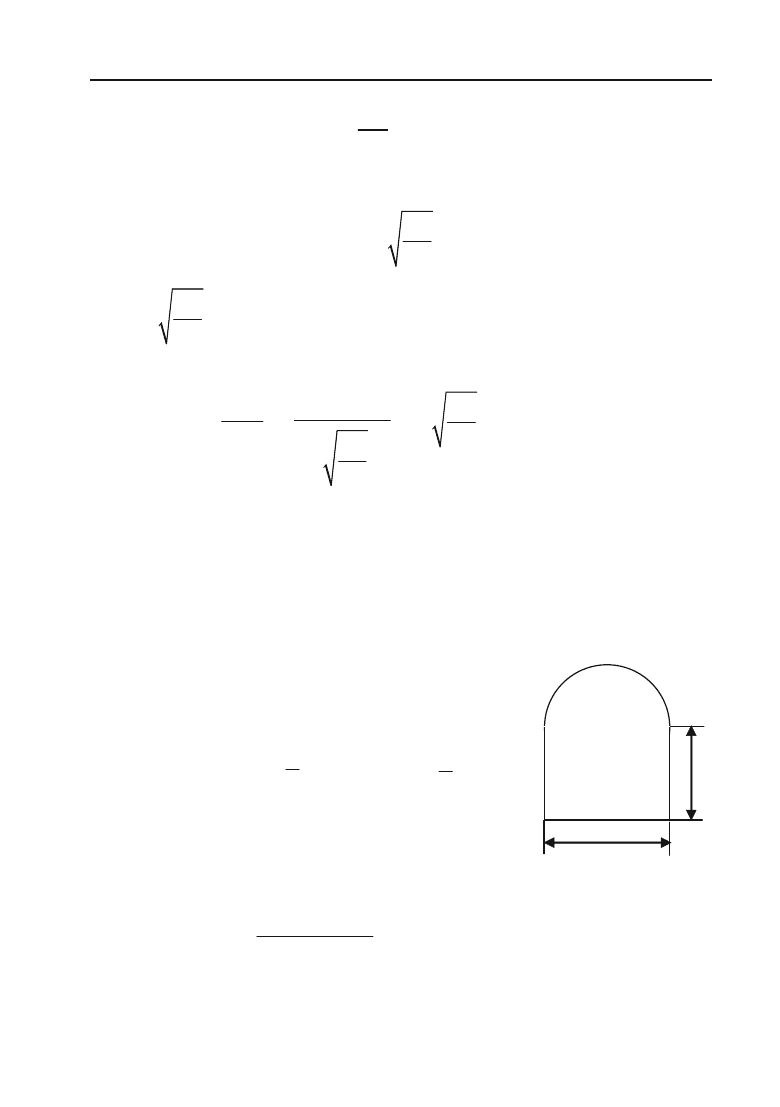
311
Розділ IV. Диференційне числення функції однієї змінної
2
4
() 4
V
SR
R
S
cc
(
R
z
0),
і при будь+якому
R
маємо, що
()
0SR
cc
!
. Із рівняння
()
0SR
c
маємо, що
3
4 R
S
–
2
V =
0
i
3
2
V
R
S
. Так як
()
0SR
cc
!
,
то значен+
ня
3
2
V
R
S
є значенням мінімуму функції, а разом з тим і наймен+
шим значенням. Запишемо значення
h
:
h =
2
V
R
S
=
2
3
2
V
V
S
S
§·
¨¸
¨¸
©¹
=
3
2
2
V
S
, тобто
h =
2
R.
Таким чином, на виготовлення циліндра заданого об’єму піде
найменша кількість матеріалу, якщо взяти висоту циліндру, рівну
діаметру.
Задача 4.57.
Вікно має форму прямокутника, завершеного
півкругом. Визначити розміри вікна, щоб вікно пропускало найбіль+
шу кількість світла, при заданому периметрі.
Розв’язок.
Нехай периметр вікна є задане
число
Р
, необхідно знайти
R
i
h
, щоб площа
вікна була найбільшою.
Площа вікна
S =
2
1
2
R
S
+
2
Rh
, де
2
1
2
R
S
—
площа півкруга, 2
Rh
— площа прямокутника.
Маємо функцію двох незалежних змінних. Ви+
разимо
h
через
R
.
Р =
S
R +
2
R +
2
h
,
h
=
2
2
PRR
S
.
Отже, площа вікна
h
2R
Рис. 4.7.
312
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
S =
2
1
2
R
S
+
2
R
2
2
PRR
S
= PR –
2
R
2
–
2
2
R
S
;
S
(
R
)
= PR –
2
R
2
–
2
2
R
S
.
Знаходимо
()
SR
c
= P –
4
R
–
S
R
;
()
SR
c
=
0;
P –
4
R
–
S
R =
0;
R =
4
P
S
;
()
SR
cc
=
–4 –
S
< 0.
А це означає, що при
R =
4
P
S
функція
S
(
R
) має максимум
знайдемо
h.
h =
2
44
2
PP
P
S
SS
=
4
P
S
.
Таким чином, щоб вікно пропускало найбільшу кількість світла,
необхідно, щоб ширина вікна була в два рази більша за висоту.
Задача 4.58.
Витрати на паливо для пароплава ділиться на дві
частини. Перша із них не залежить від швидкості і дорівнює 480
гривен за годину. А друга частина витрат пропорційна кубу швид+
кості, причому при швидкості 10 км/годину ця частина витрат дорів+
нює 30 гривен за годину. Необхідно знайти, при який швидкості сума
витрат на 1 км шляху буде найменшою.
Розв’язок
. Позначимо через
х
(км/год) — швидкість пароплава.
Тоді друга частина витрат дорівнює
kx
3
, де
k
— коефіцієнт пропорцій+
ності. Для визначення
k
підставимо
х =
10, тоді: 30 = 1000
k
, звідки
k =
30
1000
=
0,03.

313
Розділ IV. Диференційне числення функції однієї змінної
Пароплав пройде 1 км шляху за
1
x
годин. Витрати на паливо
будуть рівні: 480
1
x
+ 0,03
х
3
1
x
.
Необхідно знайти найменше значення функції
f
(
x
)
=
480
1
x
+ 0,03
х
2
на проміжку (0;
f
).
Знайдемо першу похідну:
()
f
x
c
=
–480
2
1
x
+
0,06
х.
Якщо
()
f
x
c
= 0, то
х
3
=
480
0,06
=
8000, а
х =
20.
Перевіримо, що при
х =
20 функція
f
(
x
) досягає мінімального
значення.
()
f
x
cc
=
960
3
1
x
+ 0,06;
(20)f
cc
=
960
1
8000
+
0,06 > 0.
Отже, при швидкості 20 км/год загальна сума витрат на 1 км
шляху буде найменшою.
4.8.5. Задачі для самостійного розв’язку
Задача 4.59.
Із квадратного листа жерсті з стороною а необхідно
виготовити відкриту зверху коробку, вирізавши по кутам квадрати+
ки та загнувши утворені кромки. Яка повинна бути сторона короб+
ки, щоб її об’єм був найбільший.
Задача 4.60.
Необхідно виготовити ящик з кришкою, об’єм яко+
го повинен бути рівним 72 см
3
, причому сторони основи відносились
б, як 1:2. Які повинні бути розміри всіх сторін, щоб повна поверхня
була найбільшою?
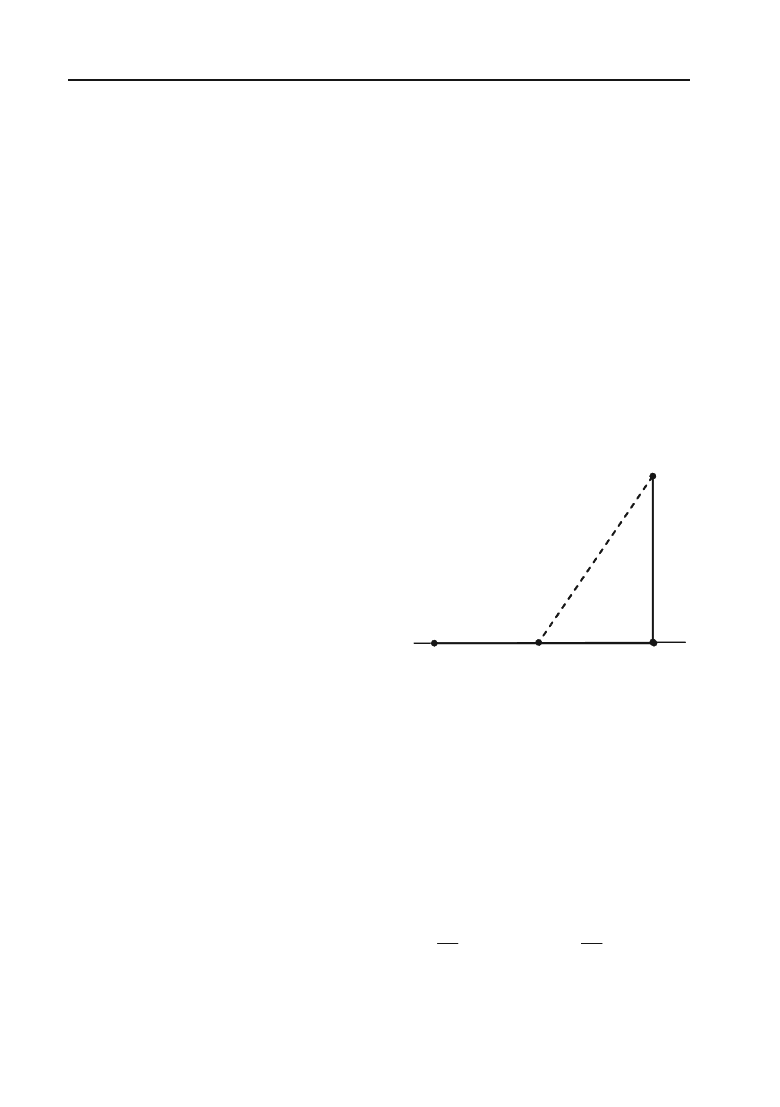
314
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Задача 4.61.
Відкритий бак має форму циліндра. При даному
об’ємі
V
які повинні бути радіус основи і висота циліндра, щоб його
поверхня була найменшою.
Задача 4.62.
На сторінці текст повинен займати 384 см
2
. Верхнє
та нижнє поля повинні бути по 3 см, праве та ліве — по 2 см. Якщо
приймати до уваги тільки економію паперу, то які повинні бути най+
вигідніші розміри сторінки.
Задача 4.62.
На сторінці текст повинен займати 384 см
2
. Верхнє
та нижнє поля повинні бути по 3 см, праве та ліве — по 2 см. Якщо
приймати до уваги тільки економію паперу, то які повинні бути най+
вигідніші розміри сторінки.
Задача 4.63.
Бак без кришки з квадратною основою повинен мати
об’єм
V
. Як повинні відноситись довжина основи до висоти баку, щоб
на його виготовлення пішла найменша кількість матеріалу.
Задача 4.64.
Завод
Д
необхідно
з’єднати шосейною дорогою з пря+
молінійною ділянкою залізниці, на
якій знаходиться місто
А
. Відстань
ДВ
по залізниці дорівнює
а
,
відстань
АВ
до залізниці дорівнює
l
. Витрати перевезень по шосе в
m
раз дорожчі вартості перевезень по
залізниці (
m
t
1). Як провести
шосе
ДР
до залізниці, щоб вартість
перевезень від заводу до міста була
найменшою.
А х Р
Д
Рис. 4.8.
4.8.6. Застосування похідної для дослідження динаміки функцій
Темп зміни функції
Розглянемо функцію
у
=
f
(
x
). Швидкість її зміни визначається,
як відомо, похідною
()
y
fx
cc
. Відносною швидкістю або темпом
зміни функції називають відношення
y
y
c
. Водночас:
(ln )
y
y
y
c
c
.
Отже, темп зміни функції дорівнює її логарифмічній похідній.
315
Розділ IV. Диференційне числення функції однієї змінної
Приклад 4.66.
Обсяг продукції
U
, виробленої підприємством
впродовж робочого дня, представлено функцією:
U
(
t
) = –
5
6
t
3
+
15
2
t
2
+ 100
t
+ 50 (од.)
1
d
t
d
8,
де
t
— робочий час, год.
Необхідно знайти:
1) продуктивність праці, швидкість і темп її зміни;
2) при якому часі
t
після початку роботи продуктивність праці
максимальна;
3) значення продуктивності праці, швидкості і темпу її зміни че+
рез
t
=
і
(
і
=
1, 8
) годин після початку роботи.
Результати обчислень звести в таблицю та проаналізувати.
Розв’язок.
1. Продуктивність праці виражається похідною
z
(
t
)
=
()
Ut
c
, а
швидкість і темпи зміни продуктивності праці – відповідно похідною
()
z
t
c
і логарифмічною похідною
Т
z
(
t
)
=
[ln ( )]
z
t
c
:
z
(
t
)
=
()
Ut
c
= –
5
2
t
2
+
15
t +
100
(од/год)
;
()
z
t
c
= –
5
t
+ 15
(од/год)
;
Т
z
(
t
)
=
()
()
z
t
z
t
c
=
2
515
5
15 100
2
t
tt
=
2
26
640
t
tt
(
1
год
)
.
2. Знайдемо максимум функції
z
(
t
):
()
z
t
c
= –
5
t +
15
=
0,
t =
3;
t =
3
— критична точка
z
(
t
);
()
z
t
c
> 0
при
t
< 3,
()
z
t
c
< 0
при
t
> 3. Звідси випливає, що
t
= 3 — точка максимуму функції
z
(
t
).
Знайдемо
z
(3):
z
(3)
= –
5
2
3
2
+
15
3 + 100 = 122,5
(од/год).

316
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Складемо таблиці значень
z
(
t
),
()
z
t
c
,
Т
z
(
t
) при
і =
1, 8
.
і z(і)
()zi
c
Т
z
(і)
1 112,5 10 0,09
2 120 5 0,04
3 122,5 0 0
4 120 –5 –0,04
5 112,5 –10 –0,09
6 100 –15 –0,15
7 82,5 –20 –0,24
8 60 –25 –0,42
Результати обчислень показують, що до кінця робочого дня про+
дуктивність праці істотно зменшується: при цьому зміна знаку
()
z
t
c
і
Т
z
(
t
) з плюса на мінус свідчить про те, що підвищення продуктив+
ності праці в перші години робочого дня змінюються її зниженням в
останні години.
4.8.7. Задачі для самостійного розв’язку
Задача 4.66.
Обсяг продукції
U,
виробленої підприємством впро+
довж робочого дня може бути заданий функцією
U = U
(
t
), 1
d
t
d
8,
де
t
— робочий час, год.
Необхідно знайти:
1) продуктивність праці, швидкість і темп її зміни;
2) при якому часі
t
після початку роботи продуктивність праці
максимальна;
3) значення продуктивності праці, швидкості і темпу її зміни через
t = і
(
і =
1, 8
) годин після початку роботи.
Результати обчислень звести в таблицю та проаналізувати.
а)
U
(
t
)
=
3
2
t
3
+
27
2
t
2
+
180
t +
80
(
од
);
б)
U
(
t
)
=
7
6
t
3
+
49
4
t
2
+
105
t +
90 (
од
)
.
317
Розділ IV. Диференційне числення функції однієї змінної
4.8.8. Опуклість та вгнутість функції
Темп зміни функції показує, наскільки одиниць збільшується чи
зменшується швидкість перебігу процесу, який описаний заданою
функцією, при кожному конкретному значенні її аргументу. Чим
вищий темп, тим швидше змінюється швидкість. Як це відображаєть+
ся на формі графіка функції? Як, маючи графік функції, відрізнити
один від одного з різними по знаку і абсолютній величині темпом?
Виявляється, графіки функції, що змінюються в додатному темпі
мають одну і ту ж властивість. Всі вони розміщені вище всіх своїх
дотичних. В зв’язку з цим, введемо поняття опуклих і вгнутих функції
та встановимо їх ознаки.
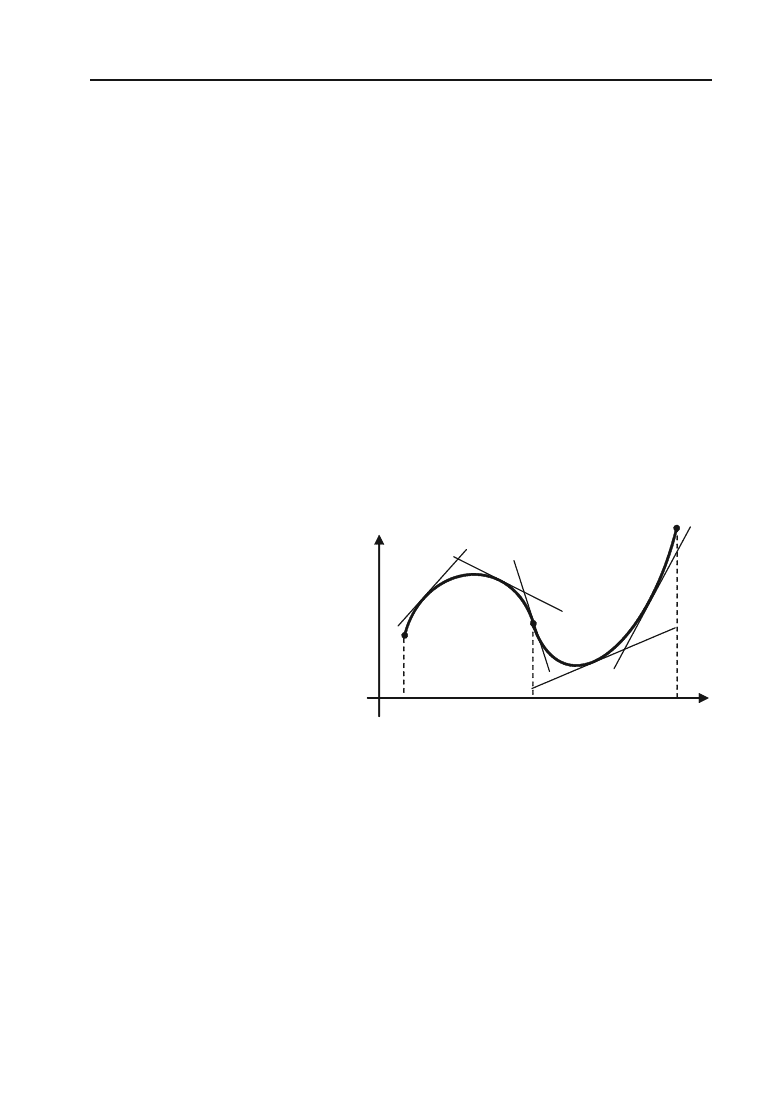
Крива
y
=
f
(
x
) називається
опуклою на інтервалі (a, b),
якщо усі
точки графіка функції лежать нижче її дотичних на цьому інтервалі.
Крива
y
=
f
(
x
) називається
вгнутою на інтервалі (b, c)
, якщо усі
точки графіка функції лежать вище її дотичних на цьому інтервалі.
Функція, зображена на рис. 4.9, на інтервалі (
a
,
b
) опукла, а на
інтервалі (
b
,
с
) вгнута.
Якщо на інтервалі (
a
,
b
)
функція
y
=
f
(
x
) визначена,
має першу і другу похідні та
()
f
x
cc
< 0 для
х
(
a
,
b
), то
функція опукла на цьому
інтервалі.
Якщо для всіх
х
(
b
,
с
)
функція
y = f
(
x
) визначена,
має першу і другу похідні та
()
f
x
cc
> 0, то функція вгнута на цьому інтервалі.
Інтервали, в яких дуги кривої опуклі, визначаються із нерівності
()
f
x
cc
< 0, а інтервали, в яких дуги кривої вгнуті, — із нерівності
()
f
x
cc
> 0.
Темп зміни функції
y = f
(
x
) виражається її другою похідною
()
f
x
cc
. Якщо на інтервалі (
a
,
b
) темп зміни функції від’ємний, то
функція на ньому опукла. Функція з додатнім темпом зміни вгнута
на відповідному інтервалі. В цьому і заключається геометричний зміст
темпу зміни функції.
0 а b c X
Y
N
M
Рис. 4.9.

318
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Точка кривої, що відділяє її опуклу частину від вгнутої називаєть+
ся
точкою перегину
. Точки кривої, в яких
()
f
x
cc
=
0 або
()fx
cc
f
,
а також ті з них, в яких
()
f
x
cc
не існує, називаються
критичними
точками другого роду
. Точки перегину необхідно знаходити серед
критичних точок другого роду. В критичній точці другого роду
х = х
0
перегин буде тільки в тому випадку, коли при переході через цю точку
()
f
x
cc
змінює знак.
Для визначення точок перегину кривої необхідно знайти всі кри+
тичні точки другого роду і розглянути знак
()
f
x
cc
в кожних двох
сусідніх інтервалах, на які ці точки поділяють область існування
функції. В випадку, якщо знаки
()
f
x
cc
в двох сусідніх інтервалах
різні, критична точка другого роду являється точкою перегину. Якщо
ж в двох сусідніх інтервалах
()
f
x
cc
має один і той же знак, то в
розглянутій критичній точці другого роду перегину немає. В точці
перегину крива перетинає дотичну.
Приклад 4.67.
Визначити точки перегину на інтервали опуклості
та вгнутості кривої
у = х
6
–
6
х
5
+
15
2
х
4
+
3
х.
Розв’язок.
Функція визначена та два рази диференційовна для
всіх
х
. Для визначення критичних точок другого роду знаходимо
()
f
x
cc
:
()
f
x
c
=
6
х
5
–
30
х
4
+
30
х
3
+
3;
()
f
x
cc
=
30
х
4
– 120
х
3
+
90
х
2
;
()
f
x
ccc
=
0,
30
х
4
–
120
х
3
+
90
х
2
= 0;
30
х
2
(
х
2
–
4
х
3
+ 3) = 0;
х
2
= 0;
х
2
–
4
х
3
+ 3 = 0;
х
1
= 0;
х
2
= 1;
х
3
= 3.
Одержані точки являються критичними точками другого роду.
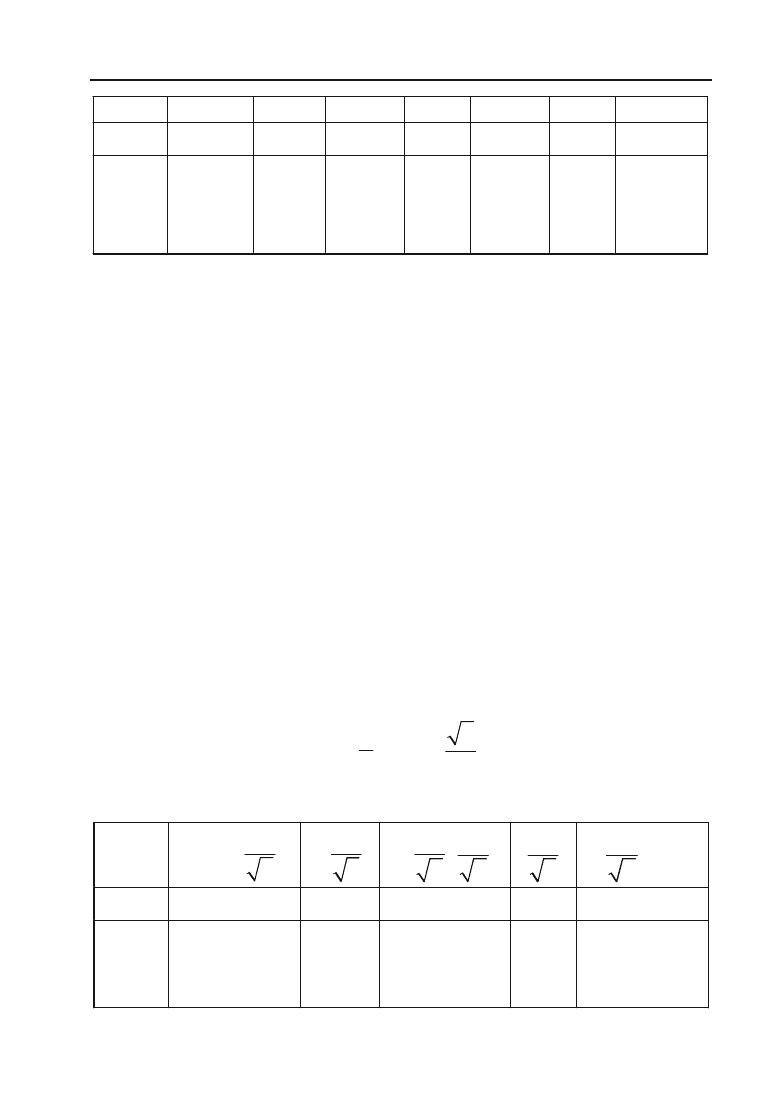
Складемо таблицю значень
()
f
x
cc
.
319
Розділ IV. Диференційне числення функції однієї змінної
Точка
х
=
0
не є точкою перегину. Точки
х =
1,
х =
3
являються
точками перегину, тому, що при переході зліва направо через ці точ+
ки друга похідна змінює знак на протилежний.
Знайдемо
у
перегину
(
х =
1) = 5,5;
у
перегину
(
х
= 3) = –112,5.
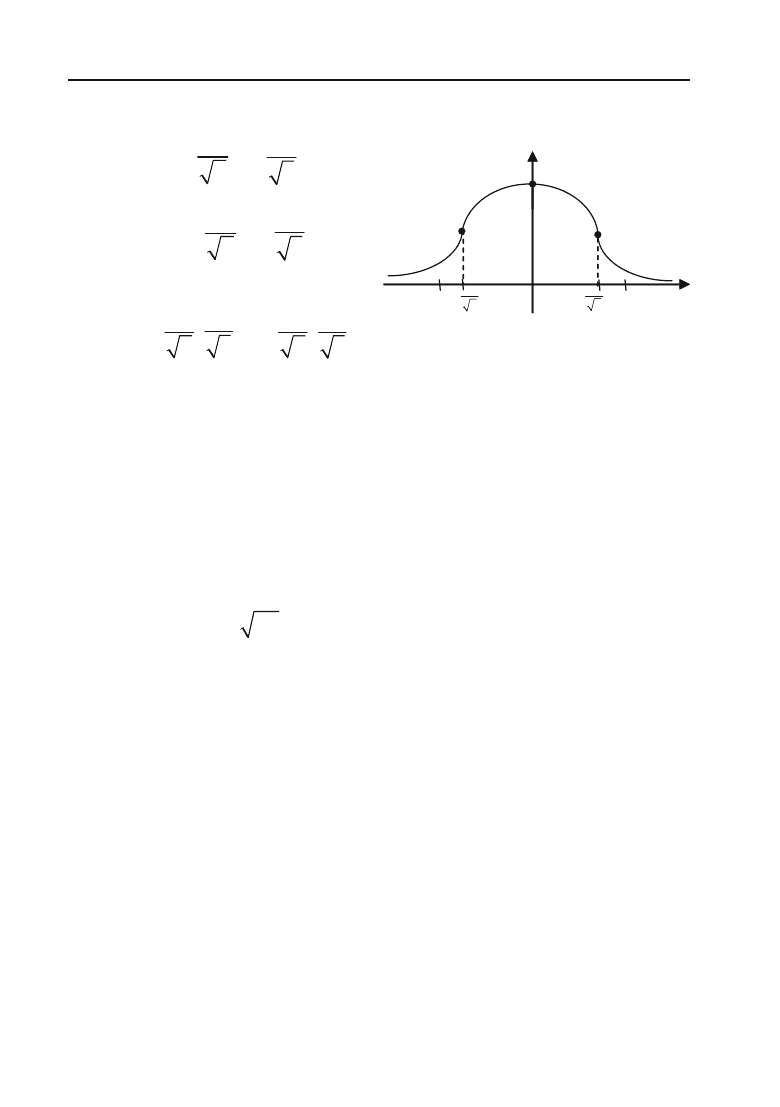
Задача 4.68.
Визначити точки перегину, інтервал опуклості та
вгнутості кривої
2
x
y
e
(крива Гауса).
Розв’язок.
Функція визначена на інтервалі (
f
;
f
). Знаходимо
першу та другу похідні:
y
c
=
2
x
e
(–2
х
)
=
– 2
х
2
x
e
,
y
cc
=
–2
2
x
e
– 2
х
2
x
e
(–2
х
)
=
–2
2
x
e
+
4
х
2
2
x
e
.
Знаходимо критичні точки другого роду:
y
cc
=
0,
–2
2
x
e
+ 4
х
2
2
x
e
= 0;
–2
2
x
e
(1 – 2
х
2
) = 0;
1 – 2
х
2
= 0;
х
2
=
1
2
,
х =
2
2
r
.
Складемо таблицю зміни знаків
y
cc
.
х (
f
; 0) 0 (0; 1) 1 (1; 3) 3 (3;
f
)
()fx
cc
+ 0 + 0 – 0 +
f(x)
крива
вгнута
нема
перегину
крива
вгнута
перегин
крив
опукла
перегин
крива
вгнута
х
(
f
;
1
2
)
1
2
(
1
2
;
1
2
)
1
2
(
1
2
;
f
)
()fx
cc
+ 0 – 0 +
f
(
x
)
крива вгнута
пере+
гин
крив опукла
пере+
гин
крива вгнута
320
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.8.9. Задачі для самостійного розв’язку
Задача 4.69.
Знайти точки перегину та інтервали опуклості і
вгнутості кривої:
1)
у
=
х
3
– 3
х
2
– 9
х
+ 9;
2)
у
=
х
+ 36
х
2
– 2
х
3
–
х
4
;
3)
у
= 1 – ln(
х
2
– 4);
4)
у
=
х
+ 2 –
5
3
x
.
Знаходимо
у
пер
(
х =
1
2
)
=
1
e
;
у
пер
(
х =
1
2
)
=
1
e
.
Отже, крива має дві точки пе+
регину: (
1
2
;
1
e
)
і (
1
2
;
1
e
).
Див. рис. 4.10.
–1
1
2
0
1
2
1 Х
у =
2
x
e
Y
1
Рис. 4.10.
4.8.10. Асимптоти
Асимптотою кривої
називається така пряма, до якої необмеже+
но наближається точки кривої при необмеженому віддаленні її від
початку координат. Крива може наближатися до своєї асимптоти
тими ж способами, як і змінна до своєї границі: залишаючись з однієї
сторони від асимптоти або з різних сторін, кілька раз перетинаючи
асимптоту і переходячи з однієї сторони на другу.
Розрізняють асимптоти: вертикальні, горизонтальні і похилі.
Для знаходження асимптот керуються наступними правилами:
а) Якщо при
х
=
а
крива
y
=
f
(
x
) має розрив ІІ+го роду, тобто
якщо при
х
o
а
– 0 або при
х
o
а
+ 0 функція прямує до нескінче+
ності (того чи іншого знаку), то пряма
х
=
а
являється вертикаль+
ною асимптотою;
