Колесников А.А. Синергетические методы управления сложными системами: теория системного синтеза
Подождите немного. Документ загружается.


u
i+1
= −f
i+1
(x
1
,...,x
n
) − z
j+1
−
D
1
D
;
.....................................
u
n
= −f
n
(x
1
,...,x
n
) − z
n
−
D
n
D
,
D=
γ
11
γ
12
... γ
1m
γ
21
γ
22
... γ
2m
... ... ... ...
γ
m1
γ
m2
... γ
mm
=0,D
1
=
Φ
1
γ
12
... γ
1m
Φ
2
γ
22
... γ
2m
... ... ... ...
Φ
m
γ
m2
... γ
mm
=0,
Φ
s
=0,
D
n
=
γ
11
γ
12
... γ
1,m−1
Φ
1
γ
21
γ
22
... γ
2m
Φ
2
... ... ... ... ...
γ
m1
γ
m2
... γ
mm
Φ
m
=0,
Φ
s
=0,
Φ
s
= γ
s1
˙v
1
(t)+γ
s2
˙v
2
(t)+···+ γ
sn
˙v
n
(t) −
1
T
s
ϕ
s
(ψ
s
).
ψ
1
=
0,...,ψ
m
=0
v
k
M
1
(t),...,M
r
(t)
•
•
•

V
s
=0, 5ψ
2
s
ψ
s
(x
1
,...,x
n
) ψ
r
=0
n −rm
ψ
s
=0

ψ
s
(ψ
1
,...,ψ
m
)

ψ
1
,...,ψ
m
ψ
m
=0
ψ
s
(ψ
1
,...,ψ
m
)
ψ
s
ψ
s
(ψ
1
,...,ψ
m
)
ψ
s
ψ
s
ψ
1
,...,ψ
m
ψ
k
(x
1
,...,x
n
)=0
ψ
k
=0
ψ
1
=0,...,ψ
m
=0
ψ
1
,...,ψ
m
ψ
k
=0
ψ
k
=0

ψ
1
=0,...,ψ
m
=0
•
•

•
•
•
˙x
i
(t)=
n
k=1
a
ik
x
k
+ F
i
(x
1
,x
2
,..., x
n
) ,i= 1,n
˙x
i
(t)=
n
k=1
a
ik
x
k
.
x
k
=0


ψ
1
=0 ψ
2
=0 ψ
m
=0
r
i
n − 1 n − 2
n − r
(n − r)
r
˙x
i
(t)=f
i
(x
1
,...,x
n
),i=1, 2,...,p;
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j= p +1,p+2,...,n− 1;
˙x
n
(t)=f
n
(x
1
,...,x
n
)+u,
x
i
x
j
f
i
(x
1
,...,x
n
)
f
i
(0,...,0) = 0 f
j
(x
1
,...,x
j
)
f
j
(0,...,0) = 0 u
p =0
˙x
1
(t)=f
1
(x
1
)+a
2
x
2
;
˙x
2
(t)=f
2
(x
2
)+a
3
x
3
;
......................;
˙x
n−1
(t)=f
n−1
(x
n−1
)+a
n
x
n
;
˙x
n
(t)=f
n
(x
n
)+u,
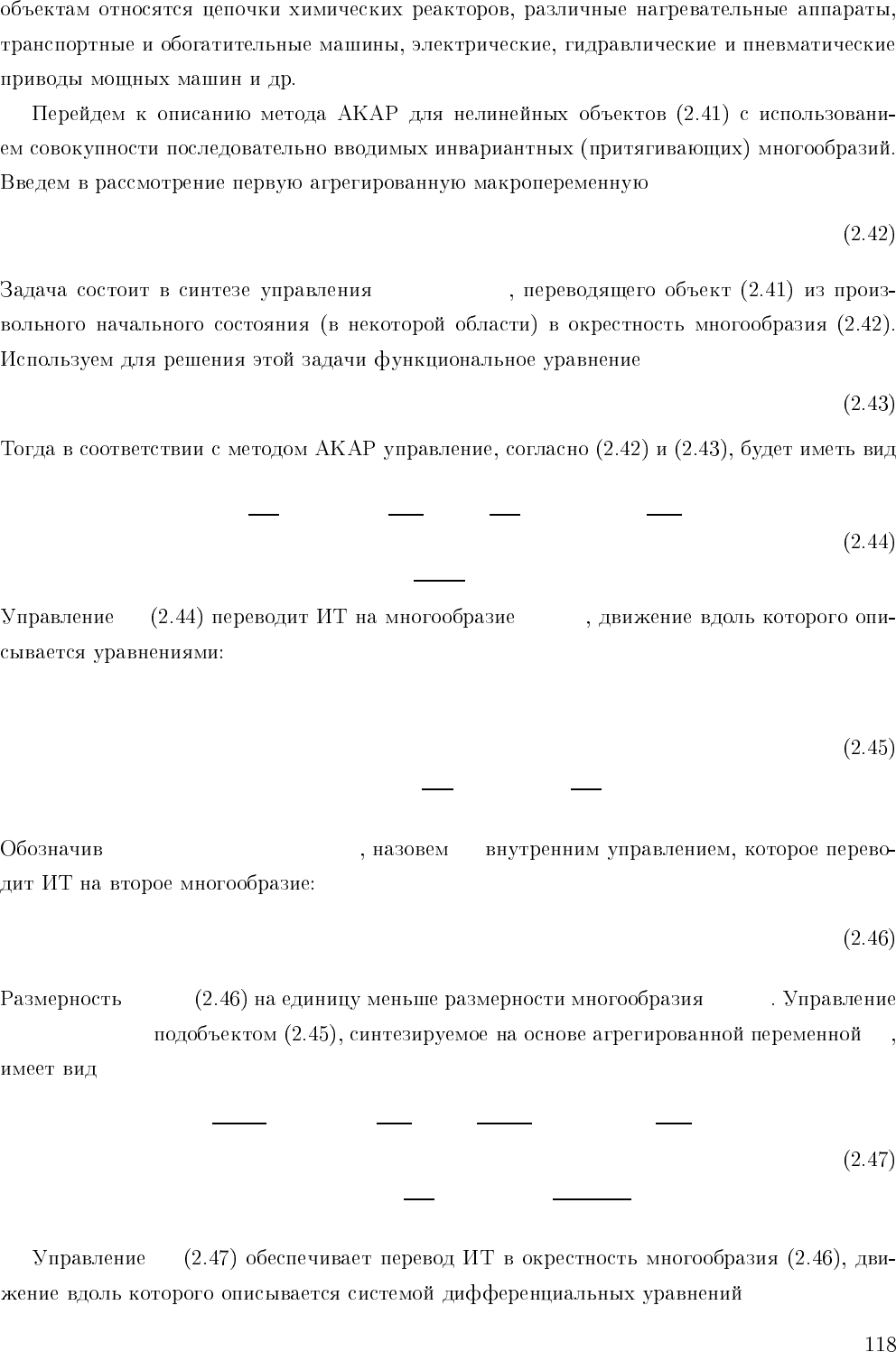
ψ
1
=
n
k=1
β
1k
x
k
+ ϕ
1
(x
1
,...,x
n−1
),
u
1
(x
1
,...,x
n
)
T
1
˙
ψ
1
(t)+ψ
1
=0.
u
1
= −
1
β
1n
p
i=1
β
1i
+
∂ϕ
1
∂x
i
f
i
−
1
β
1n
n−1
j=p+1
β
1j
+
∂ϕ
1
∂x
j
×
× (f
j
+ a
j+1
x
j+1
) −
1
β
1n
T
1
ψ
1
− f
n
.
u
1
ψ
1
=0
˙x
1
(t)=f
i
(x
1
,...,x
n
),i=1, 2,...,p;
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j= p +1,...,n− 2;
˙x
n−1
(t)=f
n−1
(x
1
,...,x
n−1
) −
a
n
β
1n
n−1
k=1
β
1k
x
k
−
a
n
β
1n
ϕ
1
(x
1
,...,x
n−1
).
β
1n
u
2
= a
n
ϕ
1
(x
1
,...,x
n−1
) ϕ
1
ψ
2
=
n−1
k=1
β
2k
x
k
+ ϕ
2
(x
1
,...,x
n−2
)=0.
ψ
2
=0 ψ
1
=0
u
2
(x
1
,...,x
n−1
) ψ
2
u
2
=
1
β
2,n−1
p
i=1
β
2i
+
∂ϕ
2
∂x
i
f
i
+
1
β
2,n−1
n−2
j=p+1
β
2i
+
∂ϕ
2
∂x
i
×
× (f
j
+ a
j+1
x
j+1
) −
a
n
β
1n
n−1
k=1
β
1k
x
k
+
1
β
2,n−1
T
2
ψ
2
+ f
n−1
.
u
2

˙x
1
(t)=f
i
(x
1
,...,x
n
),i=1, 2,...,p;
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j= p +1,...,n− 2;
............................................................;
˙x
n−2
(t)=f
n−2
(x
1
,...,x
n−2
) −
a
n−1
β
2,n−1
n−2
k=1
β
2k
x
k
−
a
n−1
β
2,n−1
ϕ
2
(x
1
,...,x
n−2
).
β
2,n−1
u
3
= a
n−1
ϕ
2
(x
1
,...,x
n−2
)
u
3
(x
1
,...,x
n−2
)
ψ
3
=
n−2
k=1
β
3k
x
k
+ ϕ
3
(x
1
,...,x
n−3
)=0.
ψ
4
=0 ψ
5
=0
ψ
l
=0
u
l
(x
1
,...,x
n−l+1
)=
a
n−l+1
β
l−1,n−l+2
ϕ
l−1
(x
1
,...,x
n−l+1
),l=1, 2,...,r;
u
l
=
1
β
l,n−l+1
p
i=1
β
li
+
∂ϕ
l
∂x
i
f
i
+ f
n−l+1
+
1
β
l,n−l+1
n−l
j=p+1
β
li
+
∂ϕ
l
∂x
i
×
× (f
j
+ a
j+1
x
j+1
) −
a
n−l+2
β
l−1,n−l+2
n−l+1
k=1
β
l−1,k
x
k
+
1
T
l
β
l,n−l+1
ψ
l
.
ψ
l
=
n−l+1
k=1
β
lk
x
k
+ ϕ
l
(x
1
,...,x
n−l
)=0
˙x
i
(t)=f
i
(x
1
,...,x
n
),i=1, 2,...,p;
˙x
j
(t)=f
j
(x
1
,...,x
j
)+a
j+1
x
j+1
,j= p +1,p+2,...,n− l +1;
..................................................................;
˙x
n−l
(t)=f
n−l
(x
1
,...,x
n−l
) −
a
n−l+1
β
l,n−l+2
n−l
k=1
β
lk
x
k
−
−
a
n−l+1
β
l,n−l+2
ϕ
l
(x
1
,...,x
n−l
),l=1, 2,...,r, r n − 1.
u
1
(x
1
,...,x
n
)
ψ
l
=0 l =2,...,r
u
l
(x
1
,...,x
n−l+1
)
