Колесников А.А. Синергетические методы управления сложными системами: теория системного синтеза
Подождите немного. Документ загружается.


˙x
1
(t)=ax
1
− bx
1
x
2
;
˙x
2
(t)=−cx
2
+ mx
1
x
2
+ u
2
.
u
2
˙x
ψ
(t)=r
ψ
(k
ψ
− x
ψ
)x
ψ
,

r
ψ
k
ψ
x
ψ0
x
ψs
= k
ψ
r
ψ
k
ψ
x
ψs
= k
ψ
k
s
ψ
k
(x
1
,...,x
n
)=0
u
2
(x
1
,x
2
)
u
2
(x
1
,x
2
)
ψ
2
(x
1
,x
2
)=β
1
x
1
+ β
2
(N −x
2
)
ψ
2
T
2
˙
ψ
2
(t)+ψ
2
=0.
˙
ψ
2
(t)
u
2
=
β
1
β
2
(ax
1
− bx
1
x
2
)+mx
1
x
2
+ cx
2
−
1
β
2
T
2
ψ
2
,
ψ
2
=0
˙x
1ψ
(t)=x
1ψ
a − bN − b
β
1
β
2
x
ψ1
.
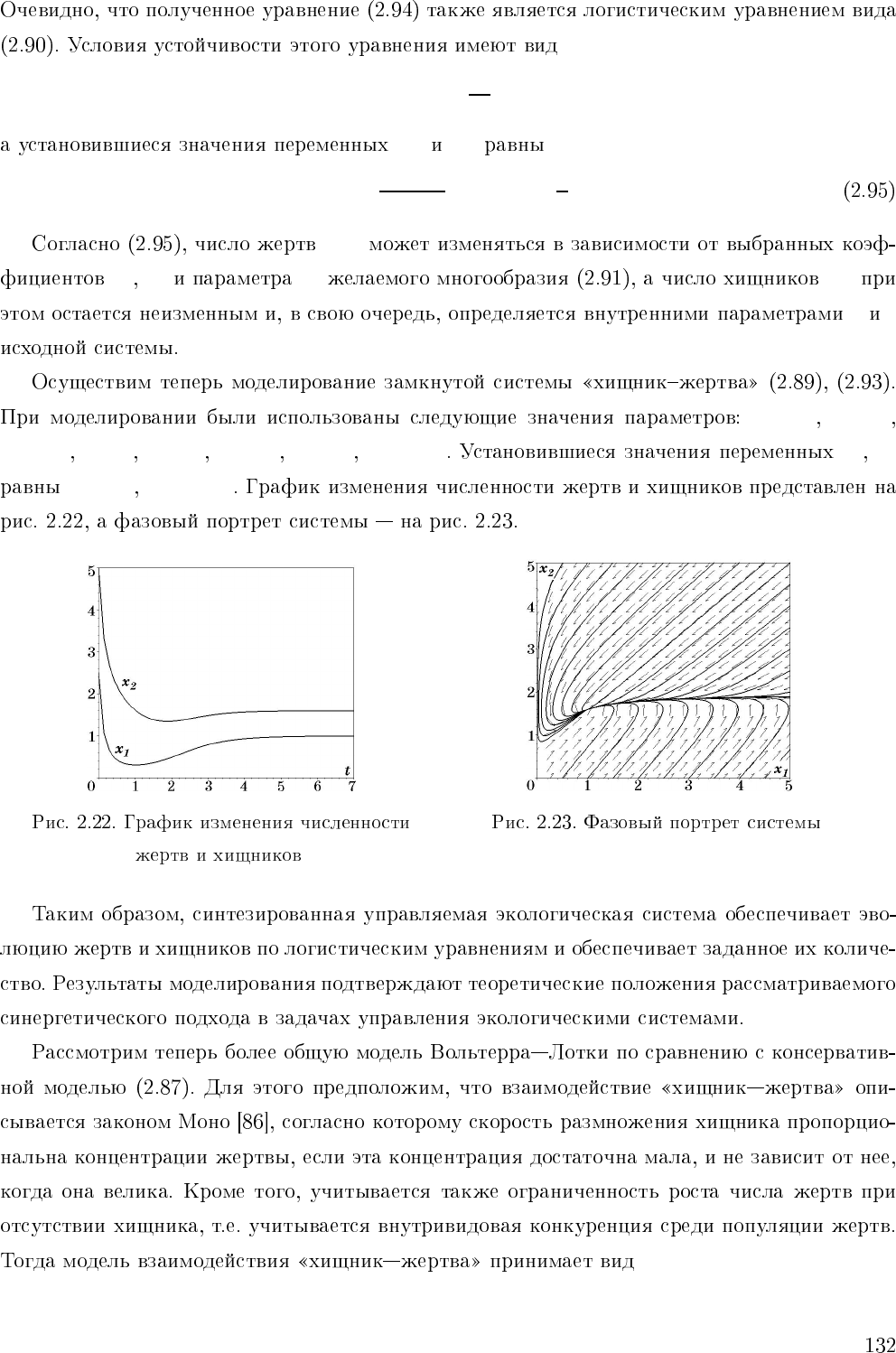
a>bN, b
β
1
β
2
> 0,
x
1s
x
2s
x
1s
=
a − bN
bβ
1
β
2
,x
2s
=
a
b
.
x
1s
z
β
1
β
2
N x
2s
a b
T =1 a =4
b =2, 5 c =2 m =1 β
1
=1 β
2
=1 N =0, 6 x
1
x
2
x
1s
=1 x
2s
=1, 6

˙x
1
(t)=ax
1
−
x
1
x
2
k + x
1
− bx
2
1
;
˙x
2
(t)=
x
1
x
2
k + x
1
− cx
2
,
a b k c>0
(x
2
=0)
˙x
1
(t)=ax
1
− bx
2
1
.
x
2
=0 x
1s
=
a
b
(b =0)
˙x
1
(t)=ax
1
−
x
1
x
2
k + x
1
− bx
2
1
;
˙x
2
(t)=
x
1
x
2
k + x
1
− cx
2
+ u
2
.
u
2
(x
1
,x
2
)
ψ = x
2
− βkx
1
− βx
2
1
,
T
˙
ψ(t)+ψ =0
u
2
= −
x
1
x
2
k + x
1
+ cx
2
+ β(k +2x
1
)
a −
x
2
k + x
1
− bx
1
x
1
−
1
T
ψ.
ψ =0
˙x
1ψ
(t)=ax
1ψ
− (β + b)x
2
1ψ
.

x
1s
=
a
β + b
,
β
x
2s
=
βa(kβ + kb + a)
(β + b)
2
.
u
2
(x
1
,x
2
)
ψ =0
T =1 a =1 b =0, 5 c =0, 5
β =0, 5
x
1s
x
2s
˙x
1
(t)=r
1 −
1
k
x
1
x
1
− αx
2
1 − exp(−λ
1
x
1
)
;
˙x
2
(t)=−bx
2
+ β
1 − exp(−λ
2
x
2
)
x
2
.
(x
2
=0)
˙x
1
(t)=r
1 −
1
k
x
1
x
1
,
x
1s
=ln
1+
b
β
−
1
λ
2
; x
2s
=
r
k
x
1s
1 −
x
1s
k
1 −
1+
β
b
λ
1
λ
2
.
r k α b λ
1
λ
2

˙x
1
(t)=r
1 −
1
k
x
1
x
1
− αx
2
1 − exp(−λ
1
x
1
)
;
˙x
2
(t)=−bx
2
+ β
1 − exp(−λ
2
x
2
)
x
2
+ u
2
.
u
2
(x
1
,x
2
)
ψ = x
2
− γx
1
,
T
˙
ψ(t)+ψ =0
u
2
= γr
1 −
1
k
x
1
x
1
− x
2
γk −γk exp(−λ
1
x
1
) − b + β − β exp(−λ
2
x
2
)
−
1
T
ψ.
ψ =0
˙x
1ψ
(t)=
r − αγ −
r
k
x
1ψ
+ αγ exp
− λ
1
x
1ψ
x
1ψ
.
exp
− λ
1
x
1ψ
≈−λ
1
x
1ψ
˙x
1ψ
(t)
∼
=
r − αγ −
r
k
+ αγλ
1
x
1ψ
x
1ψ
.
x
1s
≈
k(r − αγ)
r + kαγλ
1
; x
2s
= γx
1s
.
rx
1s
− αγk exp
− λ
1
x
1s
= k(r − αγ).
γ
x
1s
x
2s
= γx
1s
u
2
ψ =0
r = k = α = β =1 T =1 b =0, 5 λ
1
=1 λ
2
=1, 5 β =1

˙x
1
(t)=(a − ax
1
− bx
2
)x
1
;
˙x
2
(t)=(c − cx
2
− mx
1
)x
2
+ u
2
.
x
1s
=
c(a − b)
ac − bm
; x
2s
=
a(c − m)
ac − bm
,
a>b c>m
u
2
=0
u(x
1
,x
2
)
ψ = x
2
− βx
1
.
ψ
T
˙
ψ(t)+ψ =0,
u = β(a − ax
1
+ bx
2
)x
1
− (c − cx
2
− mx
1
)x
2
−
1
T
ψ,
ψ =0
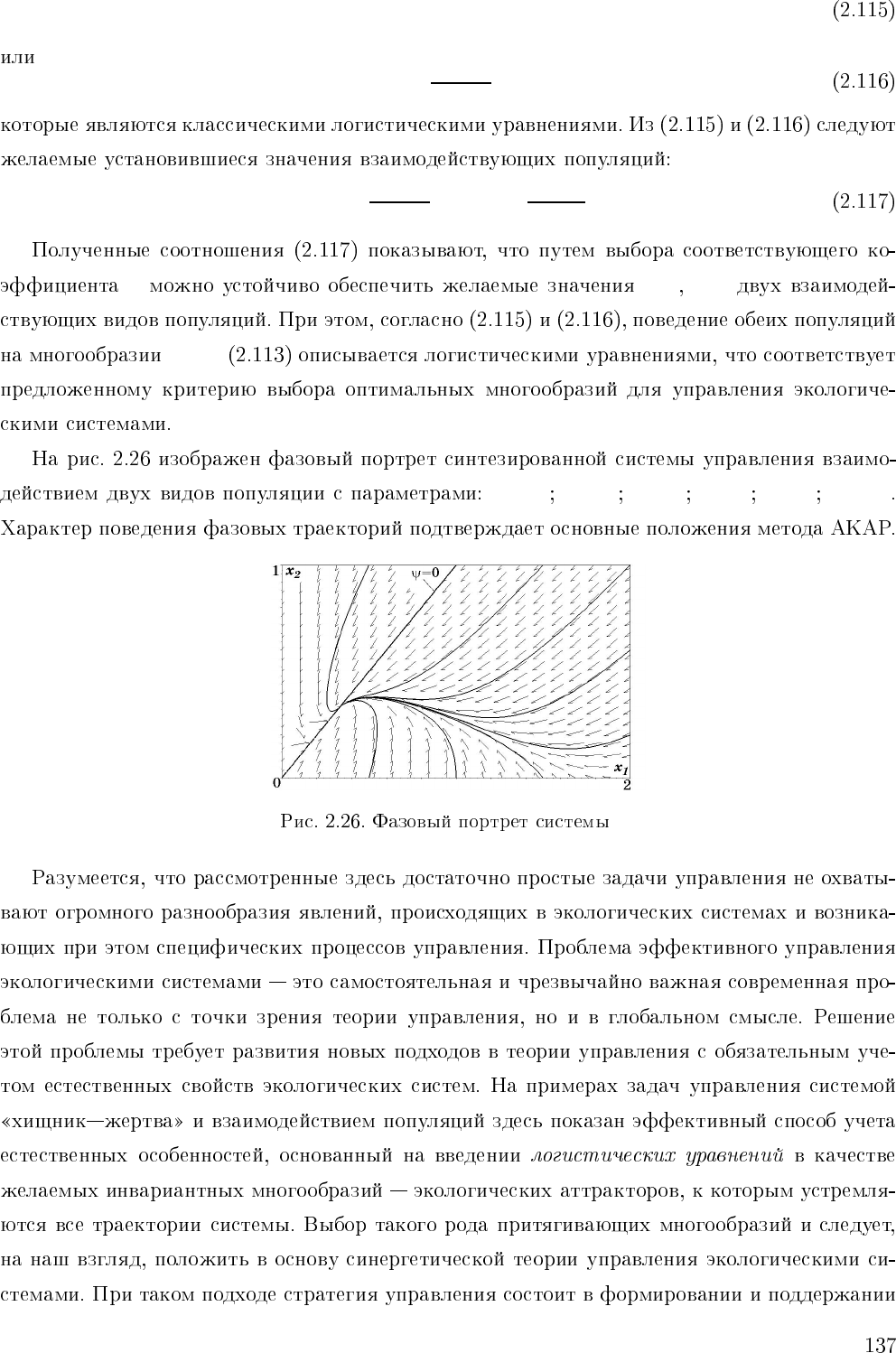
˙x
1ψ
=
a − (a + βb)x
1ψ
x
1ψ
˙x
2ψ
=
a −
a + βb
β
x
2ψ
x
2ψ
,
x
1s0
=
a
a + βb
; x
2s0
=
βa
b + βb
.
β x
1s0
x
2s0
ψ =0
T =1 β =1 a =1 b =2 c =2 m =1

˙x(t)=µ(s)x − Dx,
˙s(t)=DU −αµ(s)x − Ds,
µ(s)=
µ
m
s
k
m
+ s
.
s x
D α
s
µ(s)x Dx
αµ(s)x

DU Ds
U(x, s)
˙x(t)=r(A − x)x,
A r>0
ψ = µ(s) − r(A − x) − D.
ψ
T
˙
ψ(t)+ψ =0,
DU(x, s)=αµ(s)x + Ds −
(k
m
+ s)
2
µ
m
k
m
rµ(s)x −rDx +
1
T
1
ψ
1
.
ψ =0
x
k
= A 3T ψ =0
ψ =0 r
