Колесников А.А. Синергетические методы управления сложными системами: теория системного синтеза
Подождите немного. Документ загружается.


T
l
˙
ψ
l
(t)+ψ
l
=0,l=1, 2.
u
l
i i +1
ψ
1
,...,ψ
r
i i − 1
ψ
i
=0
ψ
i
=0
u
1
(x
1
,...,x
n
)
ϕ
1
(x
1
,...,x
n−1
) n−1
∂ϕ
1
∂x
j
ϕ
1
(x
1
,...,x
n−1
)
ϕ
2
(x
1
,...,x
n−2
),...,ϕ
r
(x
1
,...,x
n−r
)
u
l
(x
1
,...,x
n−l+1
)
ϕ
r
(x
1
,...,x
n−r
)
r ϕ
r−1
(x
1
,...,x
n−r+1
)
ϕ
r−2
(x
1
,...,x
n−r+2
)
u
l
(x
1
,...,x
n−l+1
)
u
l
ψ
l
=0
u
l
ψ
l
ϕ
l
ϕ
r
=
n−r+1
k=1
β
rk
x
k
+ ϕ
r
(x
1
,...,x
n−r
).
ϕ
r
(x
1
,...,x
n−r
) β
i
r i

r
ψ
r
=0
T
l
˙
ψ
l
(t)+ψ
l
=0,l=1, 2,... .
t
Σp
(4 ...5)
r−1
l=1
T
l
+ t
ψr
,
t
ψr
ψ
r
=0
n r
n − r
˙x
1
(t)=ax
3
1
+ x
2
;˙x
2
(t)=u.

a>0
x
2
(t) → 0 x
1
(t) →∞
u(x
1
,x
2
)
x
1
→ 0 x
2
→ 0
ψ
ψ
1
= x
2
+ βx
1
+ bx
3
1
.
T
1
˙
ψ
1
+ ϕ(ψ
1
)=0,
u
1
(x
1
,x
2
)=−
3bx
2
1
+ β
ax
3
1
+ x
2
−
1
T
1
ϕ(ψ
1
),T
1
> 0,
ϕ(ψ
1
)
ψ
1
=0 ϕ(ψ
1
) ϕ(ψ
1
)·ψ
1
> 0
ψ
1
=0
˙x
|ψ|
(t)=−βx
|ψ|
− (b − a)x
3
|ψ|
.
V=0, 5x
2
|ψ|
˙
V(t)=−βx
2
|ψ|
− (b − a)x
4
|ψ|
< 0.
β>0 b a T
1
> 0
˙x
1
(t)=ax
3
1
= x
2
;˙x
2
(t)=−
3bx
2
1
+ β
ax
3
1
+ x
2
−
1
T
1
ϕ(ψ
1
).
dx
1
ax
3
1
+ x
2
= −
T
1
dx
2
T
1
3bx
2
1
+ β
ax
3
1
+ x
2
+ ϕ(ψ
1
)
= dt.
ψ
1
=0 ϕ(0) = 0
ax
1
+ bx
3
1
= −x
2
ψ
1
=0
ψ
1
=0
ϕ = ψ
1
= x
2
+ βx
1
+ ax
3
1
u
1
= −
β
T
1
x
1
−
1
T
1
x
2
−
a
T
1
x
3
1
−
3ax
2
1
+ β
x
3
1
+ x
2
.
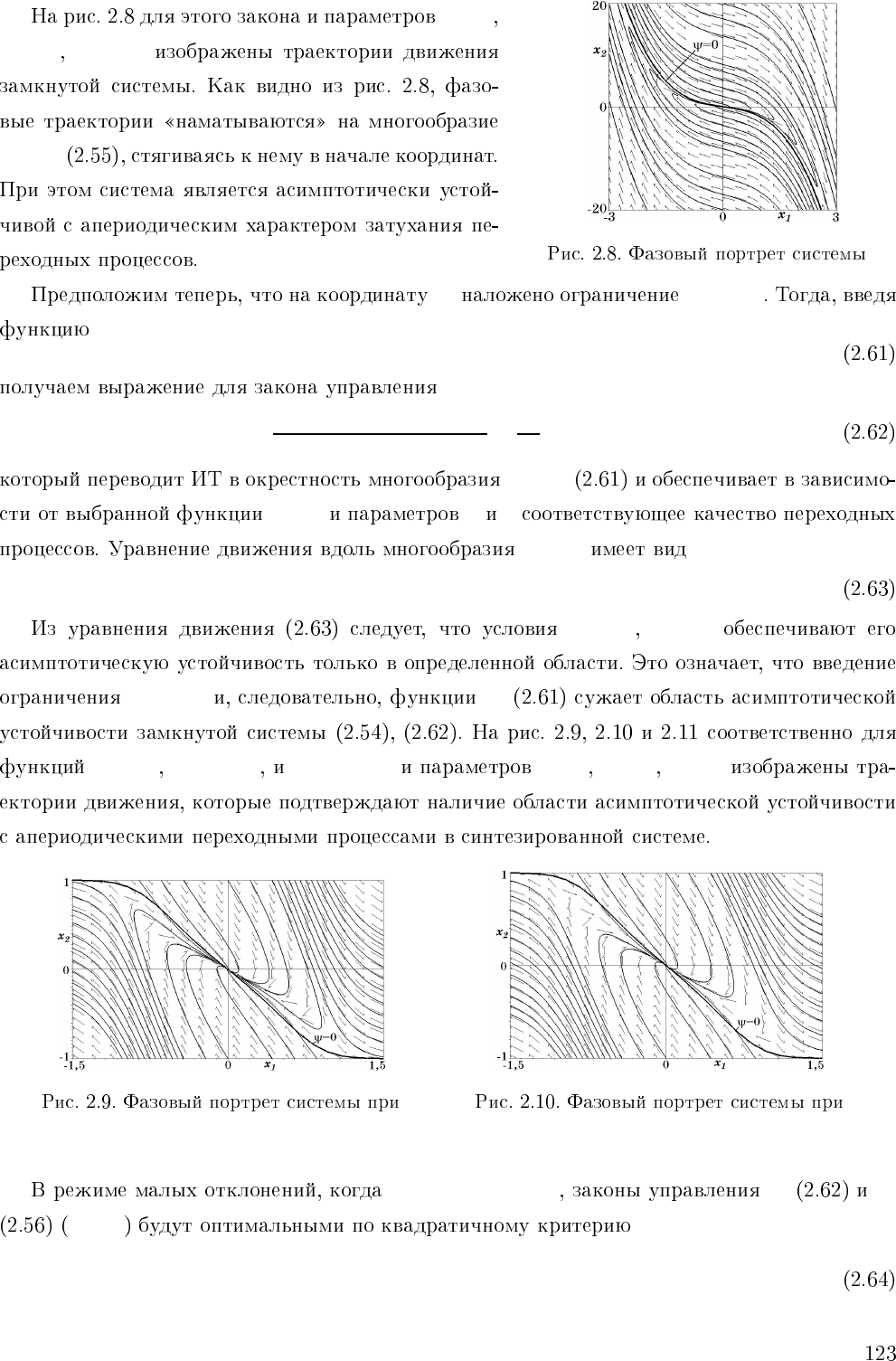
β =1
a =1 T
1
=1
ψ
1
=0
x
2
|x
2
| A
ψ
2
= x
2
+ A th(βx
1
+ βx
3
1
),
u
2
= −
A
β +3bx
2
1
ax
3
1
+ x
2
ch
2
βx
1
+ bx
3
1
−
1
T
2
ϕ(ψ
2
),T
2
> 0,
ψ
2
=0
ϕ(ψ
2
) β a
ψ
2
=0
˙x
1ψ2
(t)=x
3
1ψ2
− A th
βx
1ψ2
+ bx
3
1ψ2
.
β>0 b 1
|x
2
| A ψ
2
ϕ = ψ
2
ϕ =thψ
2
ϕ =signψ
2
b =1 T =1 A =1
ϕ = ψ
2
ϕ =thψ
2
ψ
2inf
= x
2
+ Aβx
1
u
2
u
1
A =1
J
inf
=
x
0
β
2
A
2
x
2
1
+
1+β
2
A
2
T
2
x
2
2
+ T
2
u
2
dt.

ϕ =signψ
2
u
1
u
2
|x
2
| A
˙x
1
(t)=x
2
1
+ x
2
, ˙x
2
(t)=u,
ψ = x
2
+ βx
1
+ ax
1
|x
1
|
T
1
˙
ψ(t)+ψ =0,
u = −
β
T
x
1
−
a
T
x
1
|x
1
|−
1
T
x
2
−
2a|x
1
| + β
x
2
2
+ x
2
.
ψ =0
˙x
1ψ
(t)=x
2
1ψ
− βx
1ψ
− a|x
1ψ
|x
1ψ
.
x
1ψ
=0
V=0, 5x
2
1ψ
˙
V(t)=x
3
1ψ
− βx
2
1ψ
− a|x
1ψ
|x
2
1ψ
.
x
1ψ
< 0
˙
V(t) < 0
β>0 a>0 x
1ψ
> 0
˙
V(t) < 0
β>0 a 1
β>0 a 1
x
1
= x
2
=0
β =1

T =1 a =2
m∆
¨
h(t)=a
1
δ + b
1
δ
3
; T
˙
δ(t)+δ = c
1
u,
∆h δ m a
1
b
1
c
1
T
˙x
1
(t)=x
2
;˙x
2
(t)=ax
3
+ bx
3
3
;˙x
3
(t)=−ωx
3
+ cu,
x
1
=∆h x
2
=∆
˙
h(t) x
3
= δ a =
a
1
m
b =
b
1
m
ω =
1
T
c =
c
1
T
u(x
1
,x
2
,x
3
)
x
k
(0, 0, 0)
˙y
1
(t)=y
2
;˙y
2
(t)=y
2
;˙y
3
(t)=u
0
,
y
1
= x
1
y
2
= x
2
y
3
=˙x
2
(t)=ax
3
+ bx
3
3
u
0
=
a +3bx
2
3
(−ωx
3
+ cu
1
)
ψ
1
= ρ
1
y
1
+ ρ
2
y
2
+ y
3
.
ψ
1
T
1
˙
ψ
1
(t)+ψ
1
=0,
u
0
= −
ρ
1
T
1
y
1
−
ρ
1
+
ρ
2
T
1
y
2
−
ρ
2
+
1
T
1
y
3
.
cu
1
= −
1
a +3bx
2
3
ρ
1
T
1
x
1
+
ρ
1
+
ρ
2
T
1
x
2
+
ρ
2
+
1
T
1
a + bx
2
3
x
3
+ ωx
3
.
u
0
ψ
1
= ρ
1
y
1
+ ρ
2
y
2
+ y
3
=0,
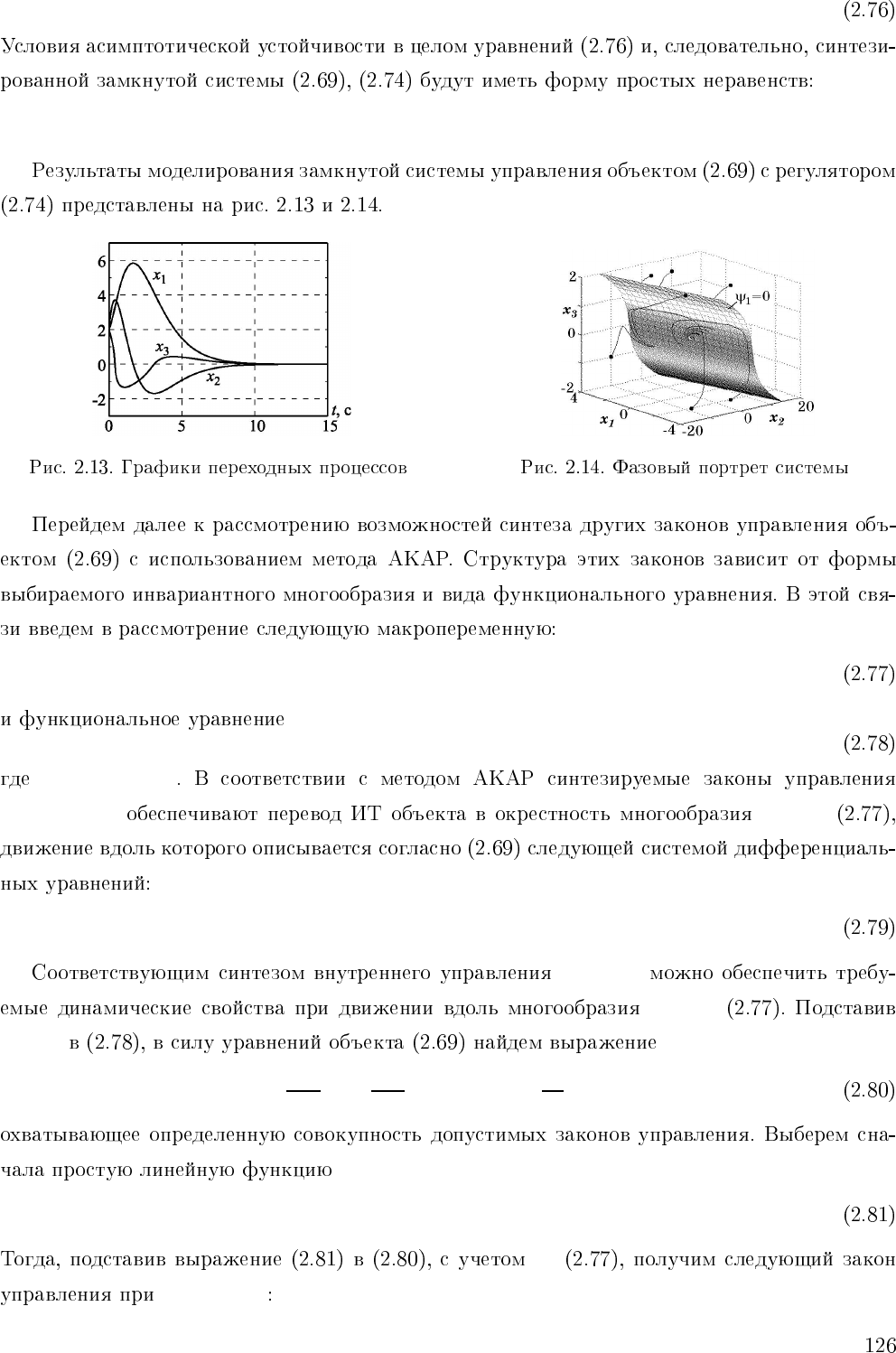
˙y
1ψ1
(t)=y
2ψ1
, ˙y
2ψ1
(t)=−ρ
1
y
1ψ1
− ρ
2
y
2ψ1
.
ρ
1
> 0; ρ
2
> 0; T
1
> 0.
ψ
2
= x
3
+ ϕ(x
1
,x
2
)
T
2
˙
ψ
2
(t)+F (ψ
2
)=0,
F (ψ
2
)ψ
2
> 0
u
2
(x
1
,x
2
,x
3
) ψ
2
=0
˙x
1ψ2
(t)=x
2ψ2
;˙x
2ψ2
(t)=−aϕ
x
1ψ2
,x
2ψ2
− bϕ
3
x
1ψ2
,x
2ψ2
.
ϕ(x
1
,x
2
)
ψ
2
=0
ψ
2
=0
cu
2
= −
∂ϕ
∂x
1
x
2
−
∂ϕ
∂x
2
a + bx
2
3
x
3
−
1
T
2
F (ψ
2
)+ωx
3
,
ϕ(x
1
,x
2
)=β
1
x
1
+ β
2
x
2
.
ψ
2
F (ψ
2
)=ψ
2
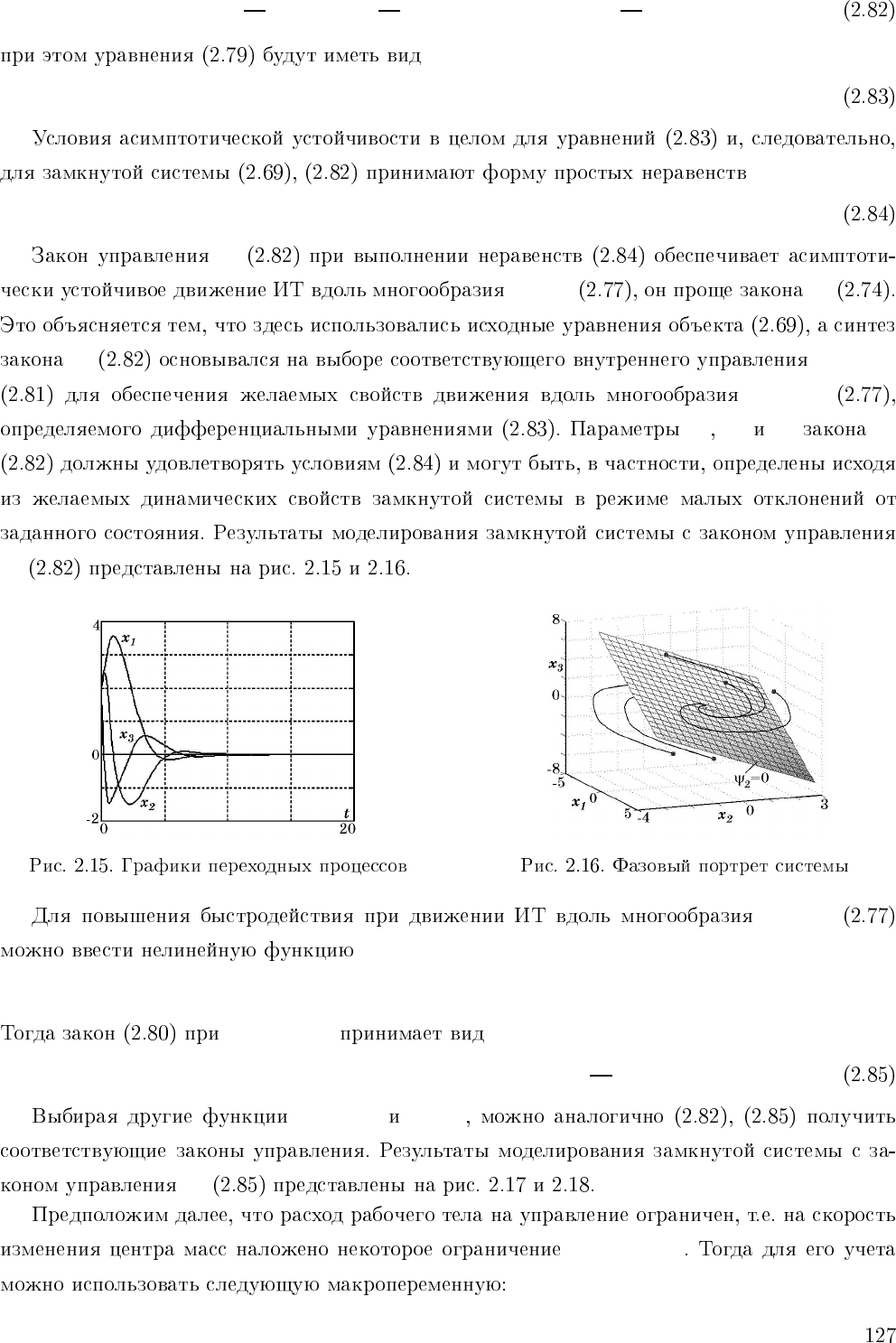
cu
2
= −
β
1
T
2
x
1
−
β
1
+
β
2
T
2
x
2
−
β
2
a + β
2
bx
2
3
+
1
T
2
− ω
x
3
,
˙x
1ψ2
(t)=x
2ψ2
;˙x
2ψ2
(t)=−β
1
ax
1ψ2
− β
2
ax
2ψ2
− b
β
1
x
1ψ2
+ β
2ψ2
3
.
β
1
> 0; β
2
> 0; T
2
> 0.
u
2
ψ
2
=0 u
1
u
2
ϕ(x
1
,x
2
)
ψ
2
=0
β
1
β
2
T
2
u
2
u
2
ψ
2
=0
ϕ(x
1
,x
2
)=β
1
x
1
+ β
2
x
2
+ β
3
x
3
2
.
F (ψ
2
)=ψ
2
cu
2
= −β
1
x
2
−
β
2
+3β
3
x
2
2
a + bx
2
3
x
3
−
1
T
2
ψ
2
+ ωx
3
.
ϕ(x
1
,x
2
) F (ψ
2
)
u
2
|x
2
| A/β
2

ψ
2
= β
2
x
2
+ A th(x
3
+ β
1
x
1
).
ψ
3
T
3
˙
ψ
3
(t)+ψ
3
=0,
cu
3
= ωx
3
− β
1
x
2
−
1
A
ch
2
x
3
+ β
1
x
1
β
2
ax
3
+ β
2
bx
3
3
+
1
T
3
ψ
3
.
|x
2
| A
x
1
x
3
ψ
3
=0
˙x
1ψ3
(t)=x
2ψ3
;
˙x
2ψ3
(t)=−β
1
x
1ψ2
− aAr th
β
2
A
x
2ψ3
− b
β
1
x
1ψ3
+ Ar th
β
2
A
x
2ψ3
3
.
β
1
> 0 β
2
> 0
x
2
|x
2
| A/β
2
x
1
x
3

˙x
1
(t)=ax
1
− bx
1
x
2
;
˙x
2
(t)=−cx
2
+ mx
1
x
2
.
x
1
(t) x
2
(t)
a b c m
x
1
x
2
(mx
1
− c)dx
1
x
1
=
(a − bx
2
)dx
2
x
2
.
c ln x
1
+ a ln x
2
− mx
1
− bx
2
= c ln x
10
+ a ln x
20
− mx
10
− bx
20
x
c
1
· e
−mx
1
= B · x
−a
2
· e
bx
2
.
B
x
10
x
20
a =4 b =2, 5 c =2 m =1
(x
1
,x
2
)
