Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

elaborated first by Eilenberger (1968), Eliashberg (1971), and Larkin and

Ovchinnikov (1977). It is much simpler to handle than the original approach

which uses the full Green functions. Fundamentals of the quasiclassical method

can be found in the review by Serene and Rainer (1983).

We turn now to definitions of the quasiclassical Green functions. Integrating over

the energy near the Fermi surface we note that it is easy to define the integrals

(5.2)

end p.78

They converge rather quickly for

T, since F and F decrease as . This

is due to the fact that the functions F and F

exist only in the superconducting

state. The integrals are, of course, determined by contributions from the

quasiparticles having energies near the Fermi surface. These quasiparticle states

correspond to the poles of the Green functions. We denote this fact by

(5.3)

(5.4)

where shows that we take the contributions from poles close to the Fermi

surface. The particle momentum lies at the Fermi surface, the only variable is the

momentum direction; we use this fact and denote

the unit vector in the

direction of p.

However, the full integral over d

diverges for the function G. This is because G

contains the normal part which decays slowly for large

. We can, however,

introduce the integral

(5.5)

which only takes the contribution from poles near the Fermi surface. With help of

eqn (3.78) the full integral over the magnitude of the momentum can be written

(5.6)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共5页 2010-8-8 11:13

where is the zero-field Green function in the normal state. In the last line,

the integral over d

converges; it is thus determined by poles near the Fermi

surface. The accuracy of this approximation is again of the order of

Since

and

we have

(5.7)

Therefore,

end p.79

(5.8)

so that

(5.9)

where means the principal value integral.

In the same way we introduce

(5.10)

so that

(5.11)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共5页 2010-8-8 11:13

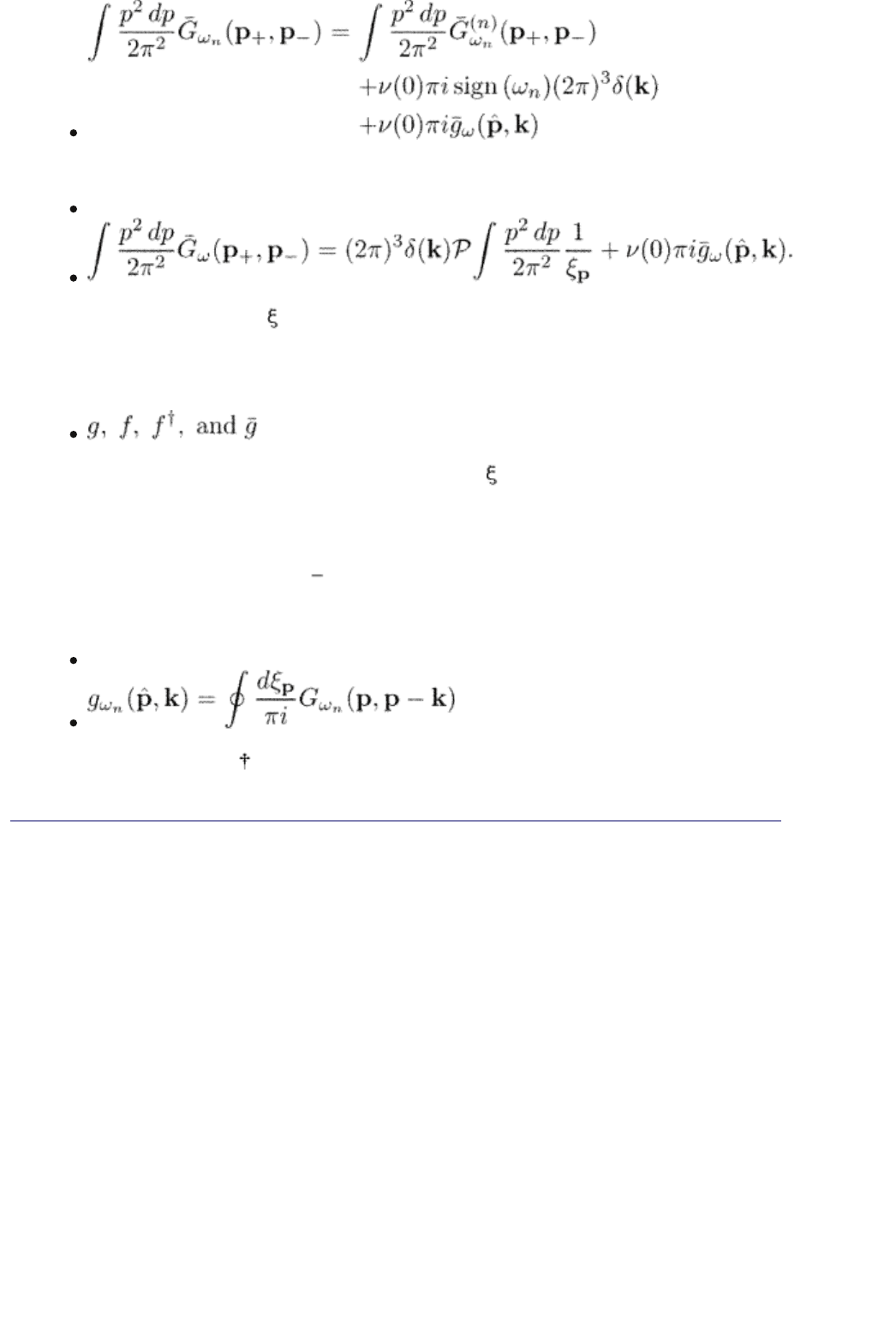
and

(5.12)

We can see that the large-

contribution to the full momentum integral of G

only depends on the properties of the material in the normal state. All the

superconducting properties are included into the functions g, f, etc., determined

by a vicinity of the Fermi surface. The functions

are called quasiclassical Green functions. The large-

contributions are

important, for example, when we calculate the density of electrons in the

superconducting state. We consider this issue in the next section.

We have defined the quasiclassical function in a symmetric way with respect to

incoming p+k/2 and outgoing p

k/2 momenta in eqns (5.3), (5.4), and (5.5).

Making shift in the momentum p, one observes that also, with the accuracy of

the quasiclassical approximation,

(5.13)

and similarly for f and f .

end p.80

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共5页 2010-8-8 11:13

Now, after the

-integration, the Green function only depends on the

momentum direction and, on the center-of-mass coordinate Fourier-transformed

into the k space. The coordinate dependence of the Green function contains

(5.14)

The integration over d

is the integration over the magnitude of the

momentum; it is equivalent to the limit r

taken along the direction of the

quasiparticle momentum p. The result thus depends on the unit vector

The term “quasiclassical Green function” means that the fast oscillations of the

Green function associated with variations of the relative coordinate r

on a

scale of

are excluded. They are not relevant to the superconducting

properties. Instead, there remains only a slow dependence on the center-of-mass

coordinate

on a scale of

characteristic to the superconducting state. Sometimes we use

a mixed Fourier-coordinate representation

(5.15)

which deals with the functions of the center-of-mass coordinate and of the

particle momentum direction.

To make the formulas more compact, we introduce the matrix notation

(5.16)

where the matrices in the Nambu space are constructed out of g, f, etc., in the

same way as the matrix

is made of G , F, etc.

5.2 Density, current, and order parameter

Using the momentum space volume element in the form of eqn (3.78) the

electron density can be written as

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [81]-[85]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:18

where

Introducing the normal-state electron density

end p.81

we find

(5.17)

Note that the procedure of taking the limit is only important for the normal-state

part of the Green function: there is no singularity in the last two terms for large

. Indeed, the sum in eqn (5.17) is

(5.18)

because the function under the sum is odd. Therefore,

(5.19)

Similarly,

(5.20)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:18

Combining eqns (5.19) and (5.20) we get

(5.21)

Note that the sums of the type of eqn (5.18) in eqn (5.21) cancel each other.

We shall see later that always

(5.22)

in a static situation. This is a consequence of the particle–hole symmetry of a

superconductor as a Fermi-liquid, i.e., the symmetry between “particles” defined

as excitations in the part of the spectrum with

> 0 and “holes” with

< 0.

end p.82

This properly holds only for quasiparticle states near the Fermi surface and is in

addition to the general relation (3.44) or (3.45). The particle–hole symmetry is

conserved in expressions for the order parameter, the current and the particle

density within the quasiclassical approximation which assumes a linear

dependence of the phase–space volume on

and uses a fixed value of the

particle moment inn magnitude |p| = p

If the density of slates and /or the

momentum magnitude are energy dependent, the particle–hole symmetry is

broken in expressions for the physical observables. In particular, the electron

density in the quasiclassical approximation does not change after a transition to

an equilibrium superconducting state:

The expression for the electric current can be transformed as follows:

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:18

The diamagnetic term in this equation, is canceled by the large-

contribution

from the normal-state Green function

, p ) in the same way as it

happened in Section 3.4. Finally,

(5.23)

Similarly,

(5.24)

end p.83

Therefore,

(5.25)

The order parameter can also be written in terms of a

-integrated Green

function. For an s-wave superconductor,

(5.26)

(5.27)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 15:18

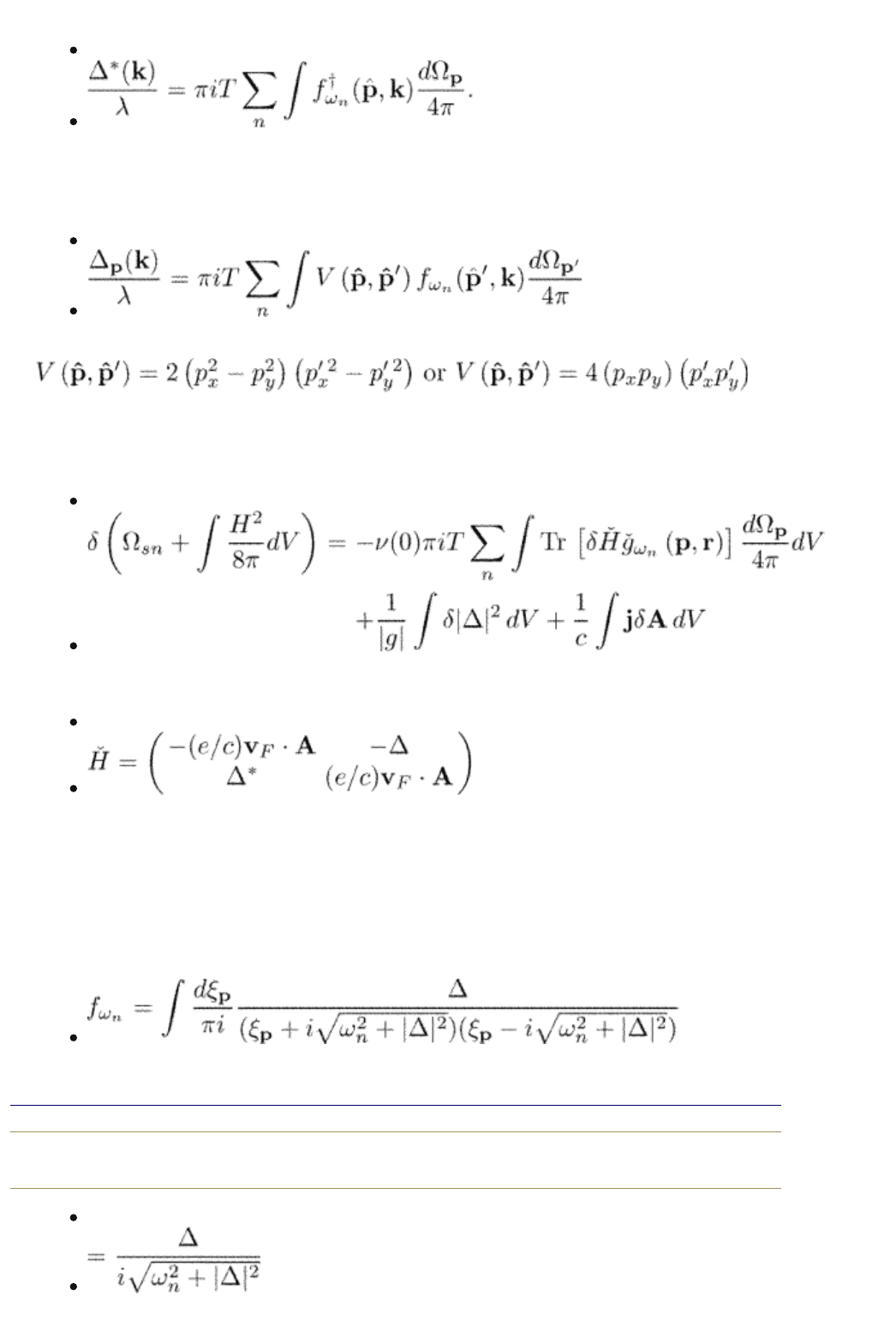
Similarly,

(5.28)

For nontrivial pairing, the order parameter equations contains the corresponding

normalized moment of the pairing potential. For example, in case of d-wave

pairing, the order parameter is

(5.29)

where

, etc. For simplicity, we assume an s-wave pairing if not specified otherwise.

Using the quasiclassical representation, one can write the expression for the

variation of the thermodynamic potential eqn (3.71) in the form

(5.30)

where now

(5.31)

instead of eqn (3.70).

5.3 Homogeneous state

For further use we calculate the functions g, f, etc., for a homogeneous case. We

have

end p.84

(5.32)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 15:18

and, similarly,

(5.33)

The integration is performed by shifting the contour of integration to either upper

or lower half-plane of

, see Fig. 3.2.

To calculate g we write

(5.34)

The two terms in the second line cancel each other. Using the contour of Fig. 3.2

we obtain from the third line

(5.35)

We find in exactly the same way

(5.36)

We see from these equations that

(5.37)

This is in agreement with the general relation eqn (5.22). Another useful relation

is the so-called normalization condition which is satisfied by the functions g, f,

and f

(5.38)

Equations (5.37) and (5.38) can be combined into one matrix equation

(5.39)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 15:18

end p.85

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 15:18