Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

this implies that g + = 0 everywhere along v

, i.e., in any inhomogeneous

situation, as well. Using this condition, we see that there are only three

independent functions, i.e., g, f, and f

which satisfy three equations

(5.83)

(5.84)

(5.85)

However, they are still not completely independent due to the normalization

condition of eqn (5.38). It was obtained for a homogeneous superconductor. To

prove it for a general case, we multiply the matrix Eilenberger equation (5.82)

first from the left and then from the right, and add the two thus obtained

equations. We have

The solution of this equation has the form

(5.86)

where A and B are constants. At large distances, i.e., in a homogeneous state

without impurities, we have A = 1 and B = 0. Therefore, they should have the

same values also for a nonhomogeneous case. This proves eqn (5.39) together

with eqns (5.37) and (5.38).

end p.93

Equations (5.83–5.85) can be written in a matrix form. Let us introduce the

matrices

(5.87)

The Eilenberger equations take the form

(5.88)

The Eilenberger equations for the real-time retarded and advanced functions are

obtained from eqns (5.83)–(5.85) by substitution i

= :

(5.89)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 15:22

(5.90)

(5.91)

Retarded and advanced Green functions also satisfy the normalization condition

(5.39). Therefore, only two of the equations (5.89), (5.90) and (5.91) are

independent.

5.6 Dirty limit. Usadel equations

The Eilenberger equations can be simplified considerably in the dirty limit (Usadel

1970), when the impurity scattering rate or the mean free path

satisfies the

condition

This limit applies only for s-wave superconductors where is independent of the

momentum direction.

A strong scattering by impurities produces averaging over momentum directions.

Therefore, in the first approximation, the Green function does not depend on the

momentum directions. The first-order correction is linear in v

. We can thus write

(5.92)

where

does not depend on directions of v

, and |g| g

; is the unit

vector in the direction of momentum. Therefore

The normalization condition gives

(5.93)

Consider a superconductor without magnetic impurities. The nonmagnetic

collision integral is determined by eqn (5.83). As we know, it vanishes after

end p.94

averaging over the momentum directions, eqn (5.77). Let us average eqn (5.88)

over directions of v

. We obtain

(5.94)

We now multiply eqn (5.88) by and average it over momenta. We have

(5.95)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 15:22

We use here eqns (5.80) and (5.81). In the dirty limit, we can neglect the terms

with . Multiplying this equation by

and using the normalization condition

eqn (5.93), we get

(5.96)

where .

Equation for the averaged functions becomes

(5.97)

where D =

F tr

/3 is the diffusion constant. In components, eqn (5.97) has the

form

(5.98)

and

(5.99)

These equations are known as the Usadel equations.

We can easily get the expression for the current from eqn (5.96):

(5.100)

The normal-state Drude conductivity is

(5.101)

In a homogeneous case, | | = const, we have

(5.102)

end p.95

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 15:22

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 15:22

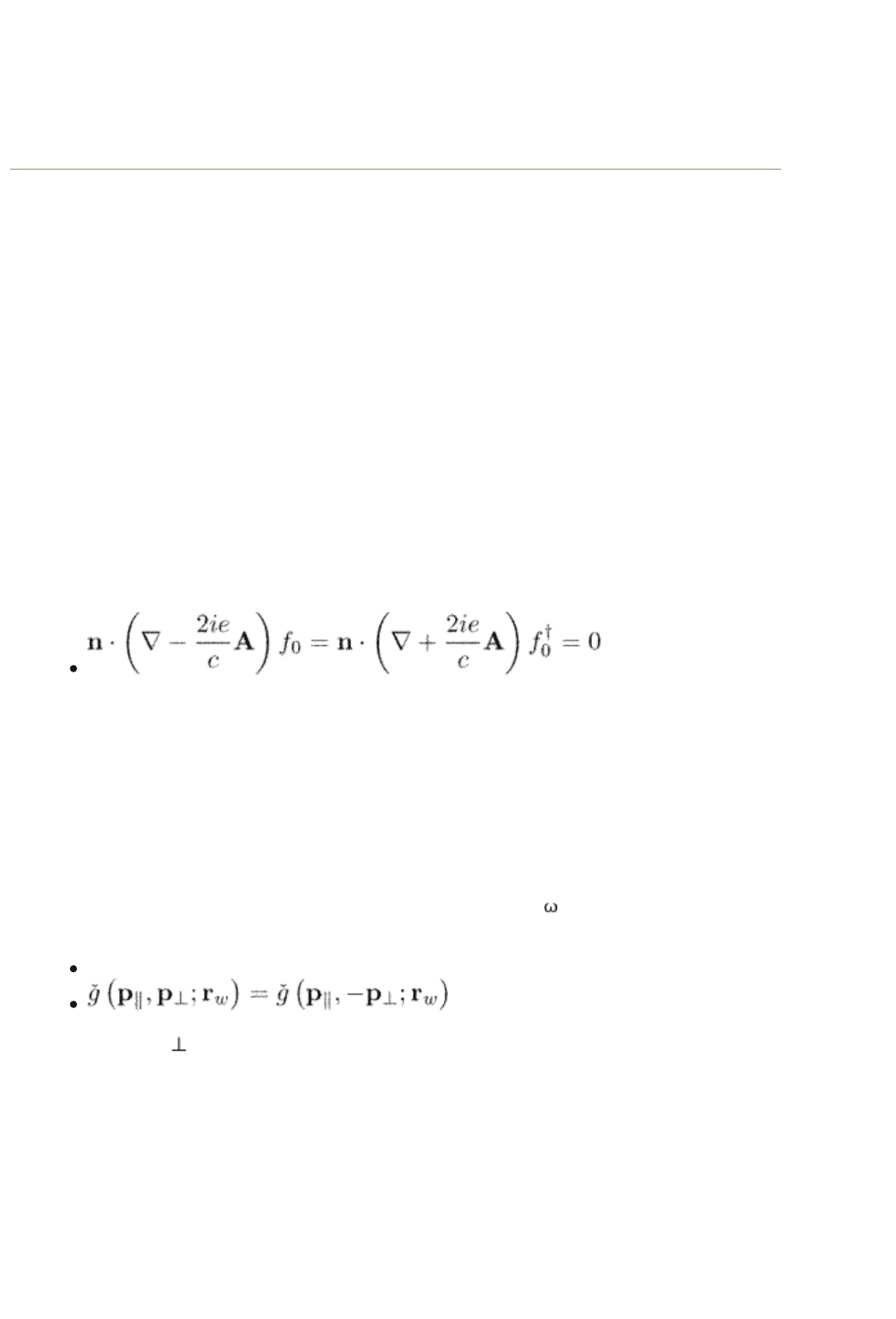
5.7 Boundary conditions

To solve the Eilenberger equations one needs some boundary conditions. They

are imposed either at the surfaces of the superconductor or in the bulk, i.e., at

large distances from those regions where the spatial dependence of the Green

functions is nontrivial. The boundary conditions in the bulk are more or loss

obvious: one has to match the obtained solution with the- Green functions for a

homogeneous situation. The boundary conditions at the surfaces depend on the

characteristics of the particular surface and vary from one surface to another. In

general, boundary conditions can be formulated in terms of the scattering

T-matrix (Serene and Rainer 1983). However, in their general form, these

conditions are rather complicated. We discuss briefly a few simple examples of

quasiclassical conditions at various boundaries.

The boundary conditions for dirty superconductors reduce to the boundary

conditions for diffusion-like Usadel equations (5.97). They are usually formulated

in terms of continuity of quasiparticle currents. For example, at the interface

between the superconductor and vacuum (non-conducting medium), the current

through the surface should vanish. According to eqn (5.100) this requires

at the boundary. Here n is the unit vector normal to the surface.

For clean superconductors, the boundary conditions are more complicated. The

whole set of conditions at interfaces between superconductors and metals or

other conducting media was derived by Zaitsev (1984).

In this section, we discuss the boundary conditions which can be imposed for a

clean superconductor at the boundary with vacuum. We consider two kinds of

surfaces. First is a completely smooth surface which is characterized by specular

reflection of incident quasiparticles. Specular reflections require that the Green

function of the reflected particle taken at the surface r = r

is equal to that

before the reflection:

(5.103)

where p

and p are the parallel and perpendicular to the surface components of

the particle momentum. Equation (5.103) automatically results in vanishing of

the current through the surface. Another example is a diffusive surface.

5.7.1 Diffusive surface

Diffusive surface reflects the incident particles randomly. The conditions at a

diffusive surface are much more complicated (Serene and Rainer 1983). First of

all, they strongly depend on the particular characteristic of the surface, for

example, on the degree of diffusivity. In certain cases, a diffusively scattering

boundary with an non-conducting medium (vacuum) is modeled by an impurity

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [96]-[100]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 15:25

layer which covers the surface. The thickness of the layer and the quasiparticle

end p.96

mean free path inside the layer are assumed to be much shorter than the

coherence length

. The specular boundary conditions are applied at the outer

side of the layer with respect to the superconductor (superfluid). To describe

various degrees of diffusivity, the ratio of the layer thickness to the mean free

path,

= d/l, varies from zero (specular wall) to infinity (diffusive wall). The

equations for the Green functions ought to be solved first inside the impurity

layer, and then the solutions should have to be matched to those in the bulk.

In this section we describe another approach where the limit

accomplished analytically for a completely diffusive surface using the method

developed by Ovchinnikov (1969). It gives the boundary conditions for the Green

functions which are to be applied directly at the boundary of the superconductor.

For a derivation of the boundary conditions it is useful to expand the

quasiclassical Green functions

(5.104)

into the three Pauli matrices in the Nambu space

(5.105)

which constitute the vector We can write

(5.106)

where n are the three expansion coefficients constituting a vector. Generally, the

components n

are functions of the coordinates and of the directions of the

quasiparticle momenta,

The vector n can be expanded into three constant, basis vectors n(N), where N

= 1, 2, 3, which satisfy the orthogonality conditions

(5.107)

where [, ]± is an anticommutator (commutator).

One can easily check that, for any two non-equal vectors n(N

) and n(N

), the

commutator

is proportional to the product of and

the third n-vector:

(5.108)

Note that the numbers N

, N

, and N

constitute an even permutation of 1, 2,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 15:25

and 3.

We can now write the Green function as follows:

(5.109)

Above, the coefficients C

are functions of r and p. Due to the normalization

end p.97

the coefficients C

satisfy the condition

(5.110)

The function in eqns (5.109) can be either retarded (advanced) or Matsubara

Green function.

The quasiparticle self-energy due to impurity scattering inside the layer is

(5.111)

where c is the impurity concentration, in the layer, and

is the scattering

cross section. The mean free time is

(5.112)

The Eilenberger equation for the Green function inside the layer has the form

(5.113)

From the definition of the impurity self-energy one has, identically,

(5.114)

Deep in the boundary layer, the Green function depends neither on the distance

form the surface of the layer nor on the momentum direction due to

isotropization in the course of the scattering. Therefore, it can be presented in

the form

with the vector n(l) independent of p and of the distance

from the surface of the layer. However, the vector n(l) may have a smooth

dependence on the position at the layer surface, r

, if the boundary is not

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 15:25

planar. We choose this vector n(l) as one of the basis vectors for the

-expansion.

One can present the Green function near the layer surface in the form

(5.115)

where the vectors n(2) and n(3) are the other two constant basis vectors. Due to

the normalization condition of eqn (4) we have

(5.116)

The coefficients C

and C

now contain all the information on the coordinate and

momentum dependencies of the Green function.

end p.98

The self-energy becomes in the boundary layer, according to eqn (5.115),

(5.117)

Using eqn (5.117) and the commutation rules of eqns (5.107, 5.108), one gets

(5.118)

This results in the equations

for the coefficients C

and C

in the layer. Here z is measured along the layer-

surface normal directed inwards the superconductor so that z < 0 corresponds to

a position inside the layer.

Like Ovchinnikov (1989), we assume that the scattering cross section,

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 15:25

nonzero only for . Using this assumption one can eliminate the

solutions which increase exponentially as z

, by requiring

(5.119)

at the surface of the layer.

There are two more conditions for the coefficients C

2,3

which follow from eqns

(5.114), (5.119) upon integration over the momentum directions:

(5.120)

Equations (5.119) and (5.120) ensure that there is no current through the

interface.

Using eqns (5.115), (5.119), and (5.120) one obtains for the basis vector

end p.99

(5.121)

where is the unit vector in the momentum direction. Since

(5.122)

and

(5.123)

one can exclude the unknown vectors n(2) and n(3) using eqn (5.116):

Since the coefficients C

and C

are coupled by eqn (5.119): C

= C

for

, and C

= C

for , one obtains

(5.124)

The conditions of eqn (5.124) can also be written directly for the functions g, f,

and f

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 15:25

(5.125)

These three equations determine the three functions g, f, and f .

These conditions hold for both the real-frequency (retarded and advanced) and

Matsubara Green functions. They are linear with respect to the functions for a

given momentum direction. This fact may be very important for practical use.

The coefficients, however, are the integrals of the functions over momentum

directions, so the boundary conditions of eqns (5.125) are nonlinear in a strict

sense.

end p.100

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 15:25