Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

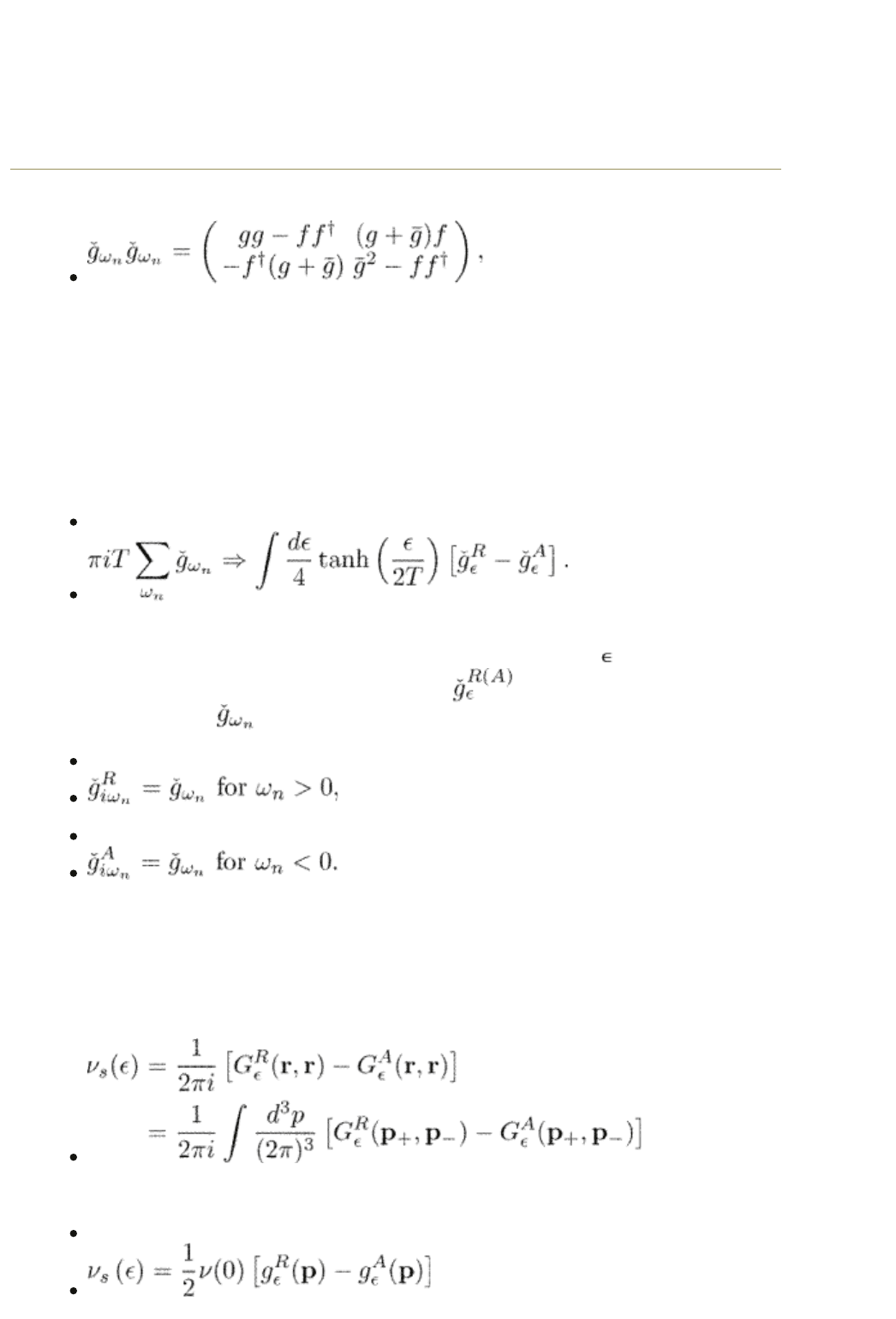
Indeed, since

eqn (5.39) is satisfied because of eqns (5.37, 5.38). We shall prove later that

eqn (5.39) holds also in a general spatially nonhomogeneous case for any

stationary situation.

5.4 Real-frequency representation

Equations for the order parameter, the current, and the particle density can be

presented in terms of real-frequency Green functions, as well, using the recipe

(5.40)

This transformation can also be used for the particle density because the

normal-state contribution vanishes due to an odd parity of tanh (

/2T). The

quasiclassical retarded and, advanced functions

can be obtained from the

Matsubara functions

by an analytical continuation using the relation

(5.41)

(5.42)

The retarded function is the Matsubara function continued analytically from the

positive imaginary axis while the advanced function is its continued from the

negative imaginary axis.

The functions g

and g

, in particular, determine the density of states. Indeed,

we know from eqn (3.62) that

is the density of states per one spin projection. We observe now that

(5.43)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [86]-[90]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:19

is the density of states near the Fermi surface (per one spin) for a given

momentum direction.

5.4.1 Example: Homogeneous state

First of all, we note that, in the normal state

end p.86

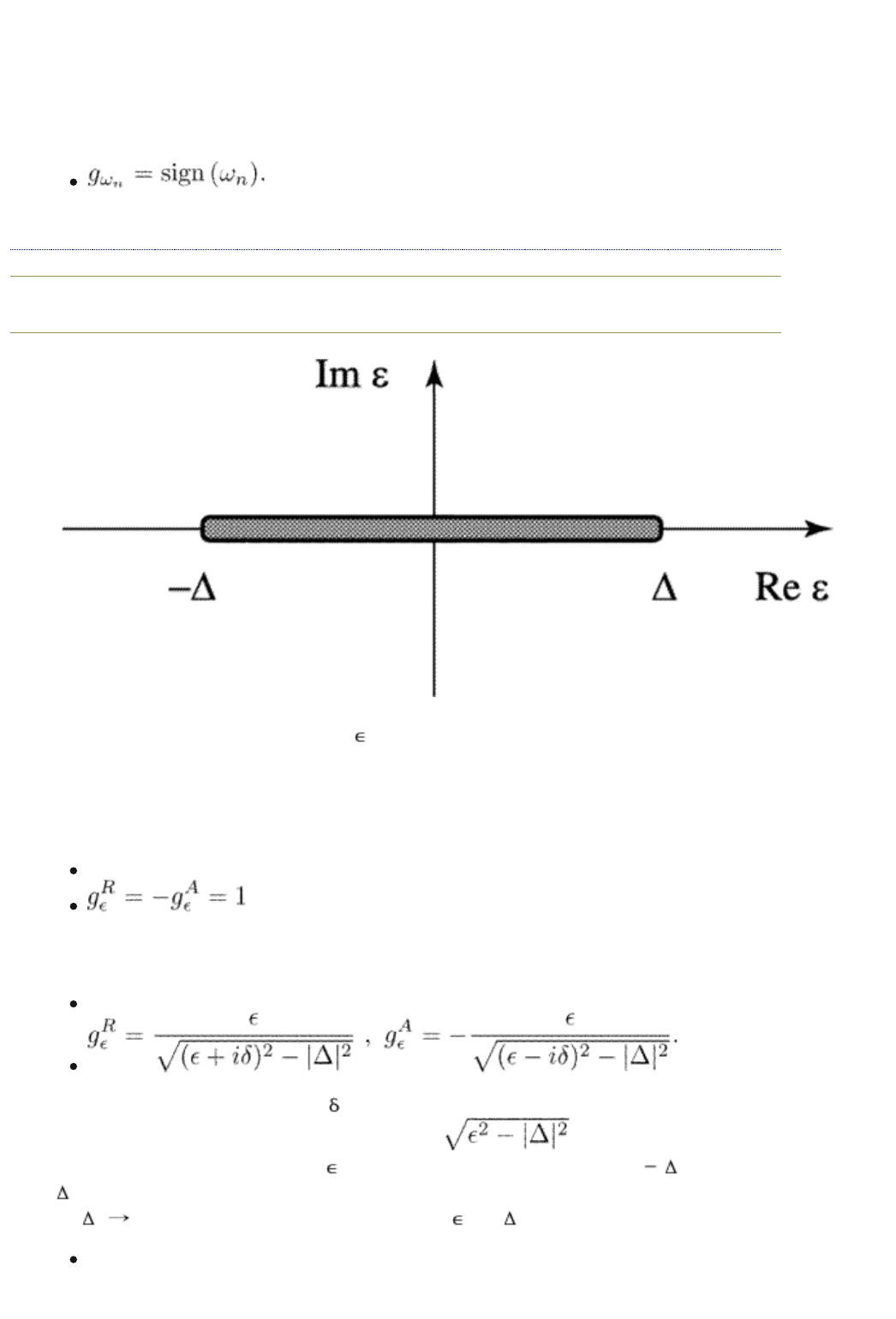
FIG. 5.1. The plane of complex with the cut. It is this plane

where the retarded and advanced functions for a homogeneous

state are defined.

Therefore,

(5.44)

in the normal state. In a homogeneous superconductor, we obtain from eqn

(5.35)

(5.45)

The infinitely small complex part i is introduced to demonstrate the analytical

properties of the functions. We can also define

as an analytical

function on the plane of complex

with the cut connecting the points | | and

| (see Fig. 5.1). This is the definition which results in eqn (5.44) in the

limit|

| 0. With this definition, we have for | | > | |

(5.46)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:19

To get the function g

in the region | | < | |, we continue the square root

to the upper edge of the cut; it becomes . To get

, we continue the square root to the lower edge of the cut; it becomes

. Therefore, we have for | | < | |

(5.47)

The functions g

R(A)

are thus “even” in for | | > | | and odd in for | | < | |.

This contrasts to

which is always odd in

. Of course, the functions

and are coupled through eqn (5.37), i.e.,

(5.48)

Similarly,

(5.49)

One has for | | > | |

end p.87

(5.50)

and

(5.51)

for | | < | |. The functions f

R(A)

are odd in for | | > | | and even in for | | <

|. Retarded and advanced function also satisfy the normalization condition of

eqn (5.39).

One can find the density of states in a homogeneous superconductor. One has

from eqn (5.43)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:19

It diverges near the gap edge and is zero for | | < | |: there are no states

within the energy gap.

5.5 Eilenberger equations

To derive equations for the quasiclassical Green functions we consider the

Gor’kov equations in the momentum representation

(5.52)

Here we use the shortcut notation

(5.53)

We write the inverse operator as

(5.54)

Here is the self-energy matrix with the components

(5.55)

The zero-order inverse operator is

(5.56)

and the effective Hamiltonian is [compare with eqn (3.70)]

(5.57)

We include the scalar electromagnetic potential into the Hamiltonian eqn

(5.57) because

= E

e while we measure energy from the Fermi level:

end p.88

= E

. We neglect k as compared to p

in the Hamiltonian since k/p

1/(p

) and omit the term

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 15:19

which is also small in the same parameter, eqn (1.61), that determines the

accuracy of the quasiclassical approximation.

The left-sided Gor’kov equation becomes

(5.58)

Similarly, the right-sided equation is

(5.59)

where

(5.60)

Let us now subtract two eqns (5.58) and (5.59). We have

(5.61)

The term with

drops out, being proportional to the unit matrix which

commutes with any matrix. We can now integrate this equation over d

near

the Fermi surface to obtain

(5.62)

With the quasiclassical accuracy, we can put everywhere |p| = p

so that

and . The product is a usual product in the

Fourier representation:

The “collision integral” is

(5.63)

It is the matrix in the Nambu space with the components

The equation for the real-frequency Green functions can be obtained by

continuation of all Green functions in eqn (5.62) onto the real frequency axis

from

end p.89

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 15:19

the positive or from the negative imaginary axis for retarded or advanced Green

functions, respectively. We have

(5.64)

where

(5.65)

Equations (5.62) or (5.64) are the famous Eilenberger equation (Eilenberger

1968) for quasiclassical Green functions. Note that the scalar potential e

disappears from the Eilenberger equations in the stationary case because it

enters

with the unit matrix and commutes with any matrix .

5.5.1 Self-energy

The self-energies can also be presented in terms of the

-integrated functions.

For example, the impurity self-energy eqn (4.10) is

(5.66)

For isotropic scattering,

(5.67)

The momentum integral can be written as

The last term gives equal positive contributions to both

and ; being

proportional to the unit matrix, it can thus be incorporated into the chemical

potential. It then drops out of the Eilenberger equation. One can write finally

(5.68)

(5.69)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 15:19

For isotropic scattering, we obtain

(5.70)

(5.71)

end p.90

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 15:19

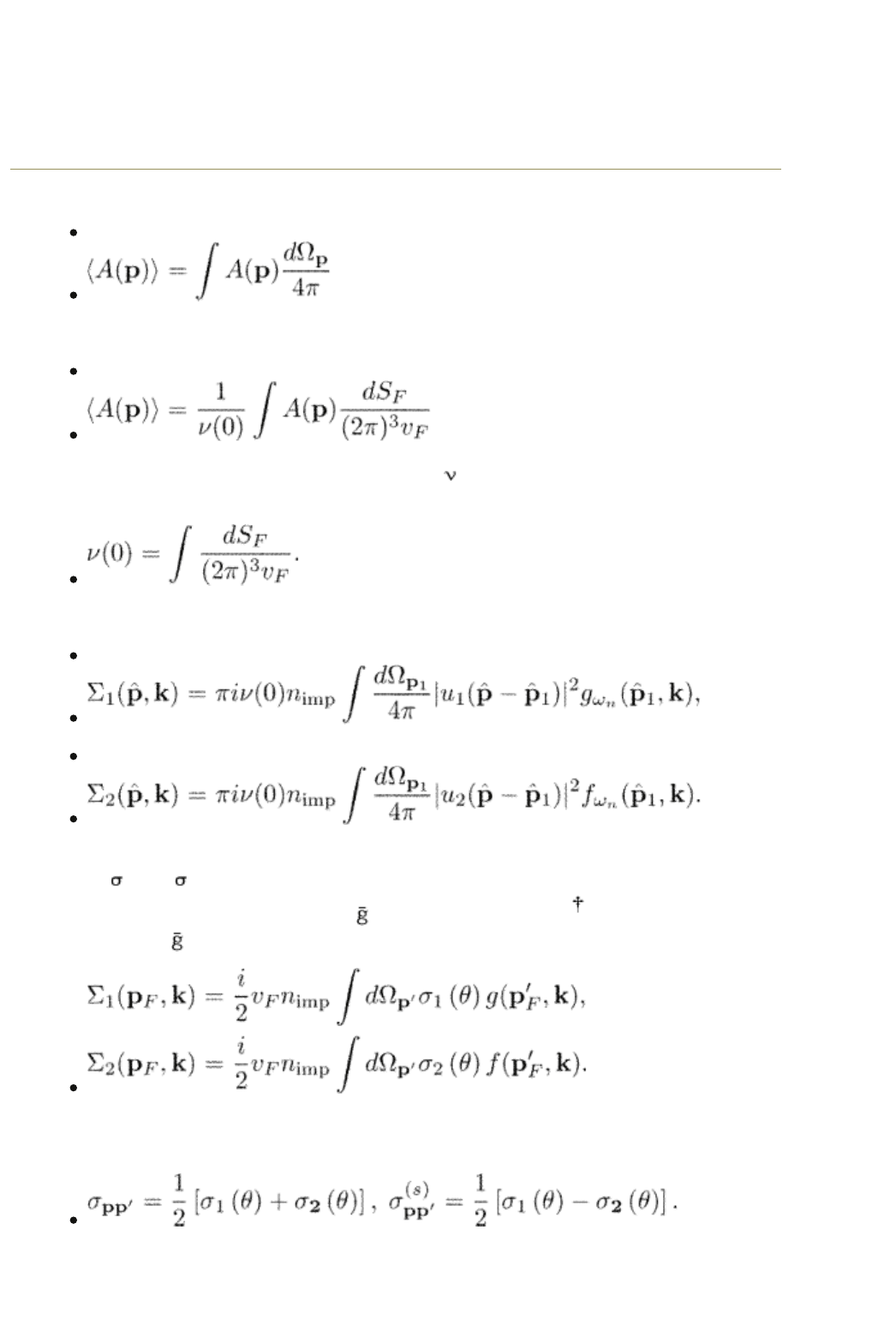
We introduce the average over the Fermi surface

(5.72)

or, more generally,

(5.73)

for a nonspherical Fermi surface. The quantity (0) here is the integrated

density of states at the Fermi surface

For magnetic impurities one has from eqns (4.14) and (4.15)

(5.74)

(5.75)

The scattering amplitudes can be parametrized by two different scattering cross

sections

and

associated with the diagonal and off-diagonal components

(i.e., with either the functions g and

or the functions f and f ) of the matrix

Green function

, respectively. As in eqns (5.74) and (5.75),

One can defne the scattering times according to eqns (4.16), (4.17) together

with the spin-flip time eqn (4.18). Let us introduce the cross sections

The spin-flip scattering cross section is positive according to eqn (4.19)

(Abrikosov and Gor’kov 1960), however, it is usually much smaller than the

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [91]-[95]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:22

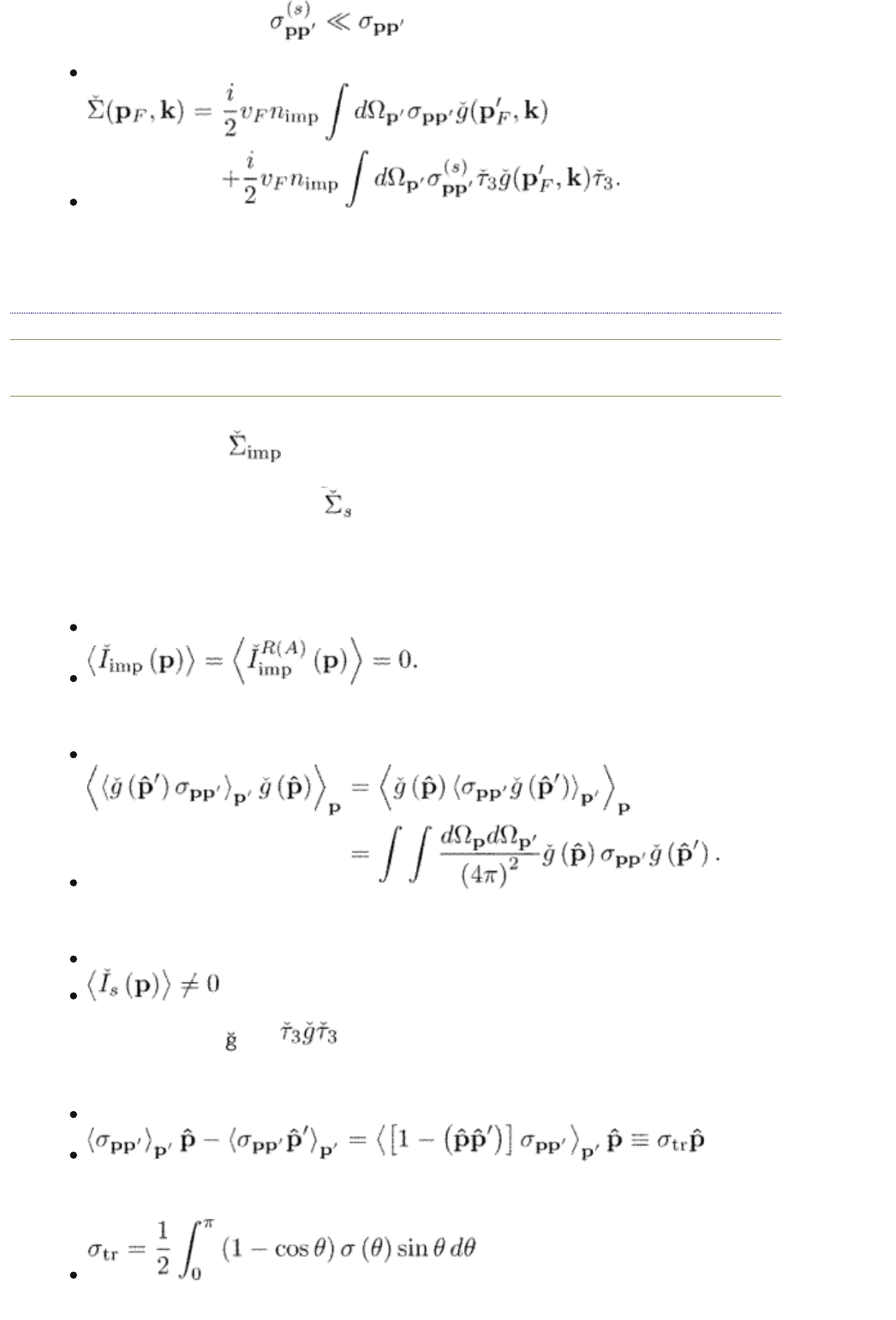
nonmagnetic cross section We can write

(5.76)

The first term describes the scattering without changes in the spin state of

electrons and coincides with the scattering by nonmagnetic impurities while the

end p.91

second term refers to the scattering accompanied by a spin-flip process. We shall

attribute the notation

only to the nonmagnetic part of the self-energy, i.e.,

to the term in the first line of eqn (5.76), and denote the spin-flip self-energy in

the second line of eqn (5.76) by

The impurity collision integral for nonmagnetic scattering eqn (5.63) or (5.65) is

expressed through nonmagnetic self-energies defined by eqn (5.76). The collision

integral vanishes after averaging over the momentum directions:

(5.77)

This is because

(5.78)

Equation (5.77) does not hold, however, for the spin-fip scattering integral:

(5.79)

because the matrices and do not commute.

Another useful relation is

(5.80)

where

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:22

is the transport cross section. To prove it we note that , should be

directed along

. Multiplying this by , we find

which proves eqn (5.80), We shall also use the transport

mean free time defined as

(5.81)

We have considered the impurity scattering in detail here. The phonon

self-energy can also be expressed through the quasiclassical Green functions. We

shall discuss this later in Section 8.2.

5.5.2 Normalization

In the mixed Fourier-coordinate representation of eqn (5.15), the Eilenberger

equation for

becomes

(5.82)

Here the product is just the usual product of two matrices. All the functions

here are functions of

and r. The matrix Eilenberger equation can be written in

components. We have

end p.92

We observe in particular that the Eilenberger equations together with the quasi-

classical functions for a stationary superconductor are invariant tinder the gauge

transformation of eqn (1.7).

From the first two equations we see immediately that g and

are not

independent:

To find the constant we assume that our superconducting state transforms

gradually into a homogeneous state without impurities at large enough distances

along the direction of v

from the region which is under consideration for a given

problem. Moreover, we assume that the magnetic field vanished at these

distances. In a homogeneous ease, the constant is zero according to eqn (5.37);

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:22