Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

6 QUASICLASSICAL METHODS IN STATIONARY PROBLEMS

Nikolai B. Kopnin

Abstract: This chapter demonstrates the potentialities of the quasiclassical

method for selected problems in the theory of stationary superconductivity. The

Ginzburg–Landau equations are derived, the upper critical field of dirty

superconductors at arbitrary temperatures is calculated, and the gapless regime

in superconductors with magnetic impurities is discussed. Effects of impurities on

the critical temperature and the density of states in d-wave superconductors are

discussed. The energy spectra of excitations in vortex cores of s-wave and

d-wave superconductors are calculated.

Keywords: Ginzburg– Landau equations, critical field, magnetic impurity,

gapless superconductivity, d-wave superconductor, vortex, energy

spectrum

We demonstrate the potentialities of the quasiclassical approach for

selected problems in the theory of stationary superconductivity: We derive

the Ginzburg–Landau equations, calculate the upper critical field of dirty

superconductors at arbitrary temperatures, and discuss the gapless regime

in superconductors with magnetic impurities. We consider effects of

impurities on the density of states in d-wave superconductors. Finally, we

find the energy spectrum of excitations in vortex cores of s-wave and

d-wave superconductors.

6.1 S-wave superconductors with impurities

6.1.1 Small currents in a uniform state

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [101]-[105]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:26

In this chapter we consider several useful applications of the quasiclassical

methods to stationary properties of superconductors. We start with a

homogeneous state of an s-wave superconductor. Without a magnetic field, the

Green functions do not depend on coordinates and on the momentum direction.

This fact tells us that

We denote the impurity scattering time simply by for brevity. Therefore, the

self-energies commute with the Green functions and drop out of the Eilenberger

equations. As a result, the homogeneous state does not depend on impurity

concentration. We know this already as the Anderson theorem. This

consideration clearly demonstrates how much simpler the quasiclassical method

is as compared to the full Green function technique: without any calculations we

have arrived to the conclusion which took two pages of algebra in Section 4.2.

Eilenberger equations (5.84, 5.85) give

Equation (5.83) vanishes. To find g and f we need to use the normalization

condition eqn (5.38). We obtain

The sign was chosen by comparison with our previous result. For retarded and

advanced functions we recover eqns (5.46), (5.47), (5.50), and (5.51).

end p.101

Consider now a superconducting state where the magnetic field and currents are

small, and the gradients are slow. The condition is

and

. The latter means that variations are slow on the scale of the

coherence length

. We also assume an isotropic scattering by impurities.

We solve the Eilenberger equations by perturbations. Let the Green function be

where

is the solution for a homogeneous state and

is a small correction

proportional to gradients and the vector potential. The first-order correction is

proportional either to the dot product of

and v

or to the dot product of A and

. It is thus linear in v

. We have therefore

The normalization condition (5.38) gives

(6.1)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:26

The corrections f

and are found from eqns (5.84) and (5.85)

(6.2)

(6.3)

We multiply the first equation by , the second equation by f

and add the two

equations. Using the normalization condition and eqn (6.1), we obtain

We find from this equation

(6.4)

The current becomes

(6.5)

where the London penetration length is found from

end p.102

(6.6)

Note that the order parameter does depend on the impurity concentration in

presence of magnetic field or current and/or in presence of order parameter

gradients because the Green function now contains the mean free time

The London penetration depth in the dirty case,

, is determined by

(6.7)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:26

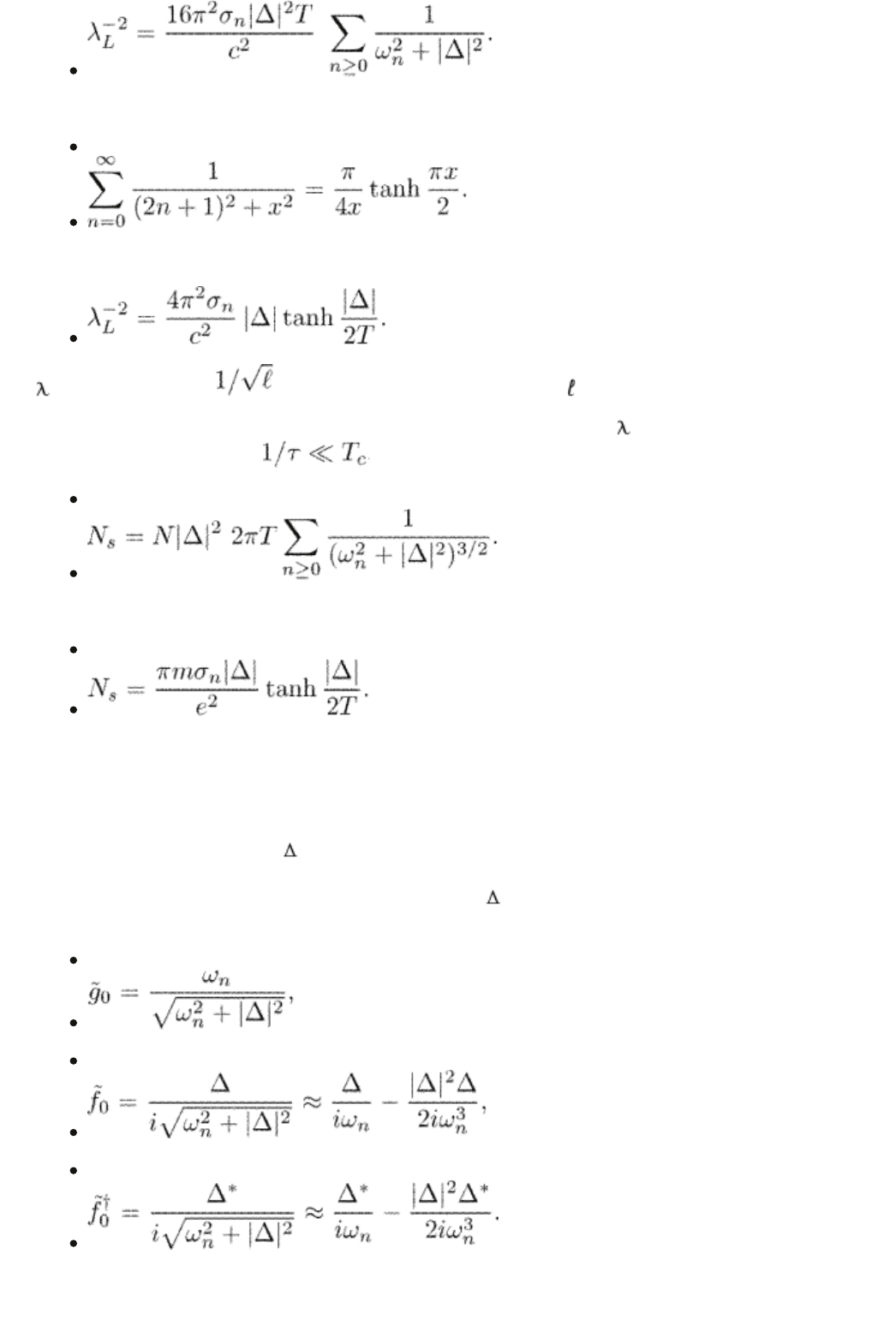
This sum can be evaluated using

(6.8)

We find

is proportional to and increases with a decrease in .

One can express the density of superconducting electrons through

using eqn

(1.25). In the clean limit,

, the superconducting density is

(6.9)

In the dirty case we have

(6.10)

6.1.2 Ginzburg–Landau theory

The Ginzburg–Landau equations can easily be derived using the quasiclassical

method. Let us assume that

and the magnetic field are small and spatial

variations of all the quantities are slow. Under these conditions, we can expand

the Eilenberger equations in small gradients and in

. Within the zero

approximation in gradients, we have for an s-wave superconductor

(6.11)

(6.12)

(6.13)

We need the function f up to the terms which are simultaneously of the

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 15:26

third-order in and zero-order in gradients, or of the second-order in gradients

and

end p.103

of the first-order in . Within the first-order in , the function g = 1. Note that

the function g contains only even powers of

. Therefore, a first-order correction

in gradients for the function g is simultaneously of the second order in

The first-order corrections both in the gradient and in

are found from eqn (6.2)

(6.14)

The correction of the second-order in gradients and first-order in is found from

Since g

is zero again, we get

(6.15)

Performing the angular averaging we solve the resulting equation for f

whence

where we use

for a spherical Fermi surface. For the third-order terms in we do not need

gradients. Therefore, the final expression for the averaged Green function is

(6.16)

The gradient-independent terms do not contain in accordance with the

Anderson theorem.

6.1.2.1 Order parameter

The self-consistency equation for the order parameter (5.27) gives

(6.17)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 15:26

In the first sum, we introduce the cut-off value as in eqn (3.81)

(6.18)

end p.104

Therefore

(6.19)

where we use the expression for the critical temperature eqn (3.83) through the

interaction constant. Next,

(6.20)

Here we use

where

is the Riemann function. The equation for the order parameter becomes

(6.21)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 15:26

where

and

(6.22)

The function

For clean superconductors the coefficient

The condition of a small is T. This is satisfied for T T

. Therefore,

ln(T

/T) 1 T/T

. We finally obtain

(6.23)

Equation (6.23) is identical to the famous Ginzburg–Landau equation (1.12) for

the order parameter. It was derived microscopically by Gor’kov (1959 a, 1959 c).

end p.105

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 15:26

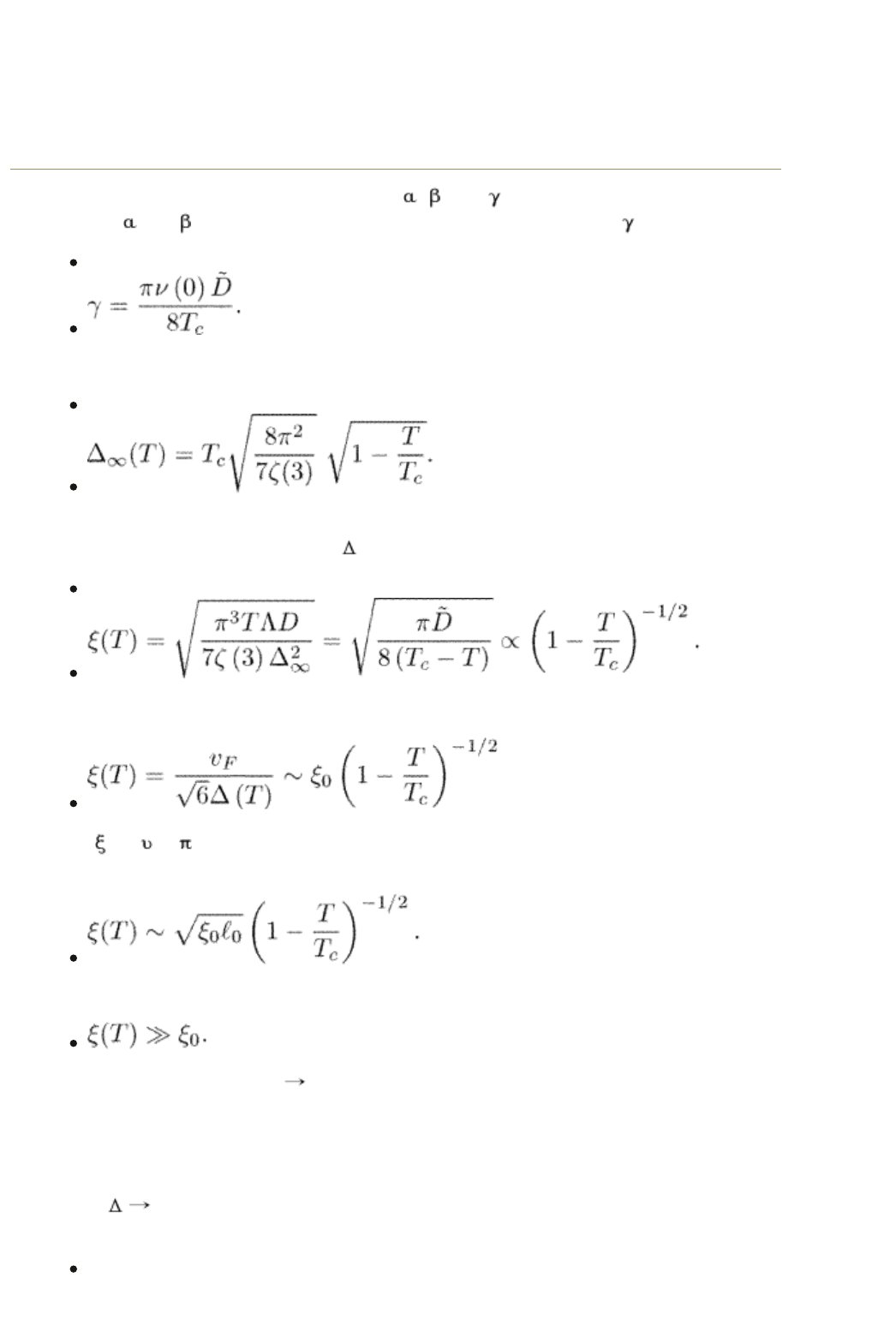
Equation (6.23) determines the constants , , and introduced on page 4. The

constants

and were already defined by eqn (1.8). The constant is

(6.24)

The equilibrium order parameter is

(6.25)

The GL equation determines the temperature-dependent coherence length, i.e.,

characteristic scale of variations of

(6.26)

We have already encountered it on page 6. For clean superconductors

where

/2 T

is the zero-temperature coherence length. For dirty

superconductors

The condition of slow variations of the order parameter implies that

This is always satisfied for T T

6.1.2.2 Current

To find the current, we can use the results obtained earlier. We take eqn (6.5)

and put

0 in the denominator. We reproduce eqn (1.13) which can be

written as

(6.27)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [106]-[110]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:28

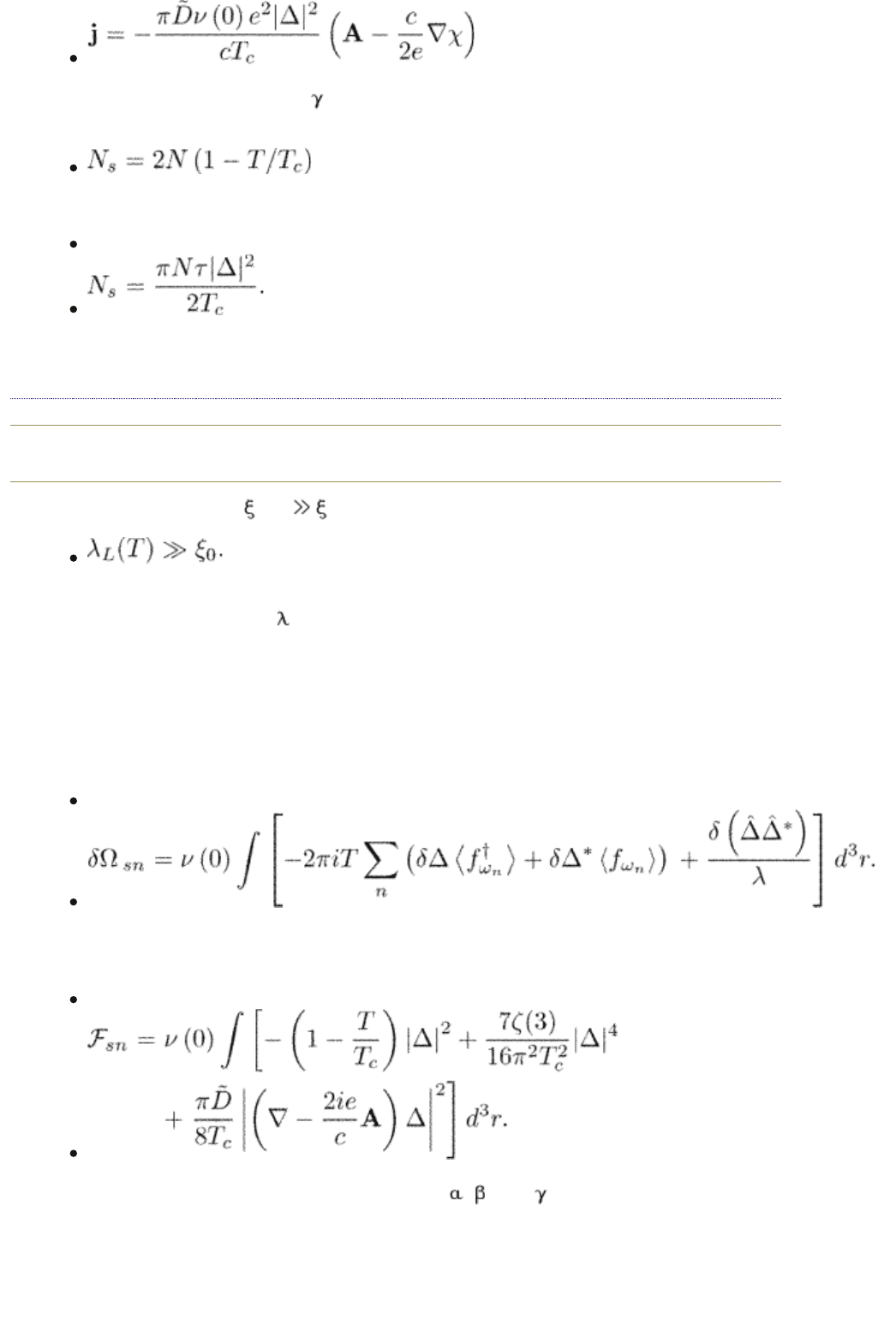
using the microscopic value for . With this expression for the supercurrent we

find, in particular, that the density of superconducting electrons is

in clean superconductors. For dirty superconductors

(6.28)

This agrees, of course, with eqn (6.6).

end p.106

Note that in addition to (T)

, the condition of slow variations implies also

It is fulfilled for both type I and type II superconductors when temperatures are

close enough to T

because

increases as T approaches T

6.1.2.3 Free energy

One can use equation (5.30) for the thermodynamic potential to find the

Ginzburg–Landau free energy of a superconductor. For a constant chemical

potential we have

(6.29)

The same expression also holds for variation of the free energy for a constant

particle density. Calculating the sums we find from eqn (6.16)

(6.30)

It coincides, of course, with eqn (1.3) for given , , and .

6.1.3 The upper critical field in a dirty alloy

Consider the second-order phase transition of a dirty alloy from normal into the

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:28

superconducting state in a decreasing magnetic field. As in Section 1.1.2, we are

going to calculate the critical magnetic field below which the superconducting

state first appears, i.e., the upper critical field H

. At this time, however, we do

not restrict ourselves to temperatures close to T

but shall use the quasiclassical

method and demonstrate that it is able to treat this problem for arbitrary

temperatures.

Near the transition, the order parameter is small. We can again expand the

Green function in a small

. In the zero-order approximation, g

= 1, and

where

has yet to be found. The Usadel eqn (5.98) gives

(6.31)

This equation has exactly the same form as the Ginzburg–Landau equation for

the order parameter near the upper critical magnetic field, eqn (1.31). We again

take the vector potential in the form

end p.107

where the magnetic field is nearly homogeneous and is directed along the z-axis

and put

(6.32)

The equation for Y(x) becomes the oscillator equation

(6.33)

The solution which appears first with decreasing the magnetic field corresponds

to the lowest level of eqn (6.33) and has the form of eqn (1.35) with

(6.34)

The full expression for is a linear combination of functions (6.32) with various

k. A periodic solution has the form of a vortex lattice, eqn (1.36), obtained by

Abrikosov (1957).

The Green function becomes

(6.35)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:28