Kothari D.P., Nagrath I.J. Modern Power Systems Analysis

Modern

Power

System

Anatysts

The

circuit

model

for

the

system

of

Example

9'3

for

computation

of

postfault

condition

is

shown

in

Fig'

9'14'

_

0.9636x

70.60

=

-

78.565

pu

Change

in

generator

current

due

to

fault'

AI^=- l8.s6s

t

io'+

-

i2'141

Pu

,,

B

_

r"."

"_

j0.60

Change

in

motor

current

due

to

fault'

At^=-

78.565

x

j.$*i

--

-

i6'424

Ptt

To

these

changes

we

add

ttre

prefault

current

to

obtain

the

subtransient

current

in

machines.

Thus

I'l=

I"

+

AIr

-

(0.623

-

j1.67$

Pu

In

=

-

I"

+

AI^=

(-

0.623

-

76.891)

Pu

which

are

the

same

(and shoutd

be)

as

calculated

already

we

have

thus

solved

Example

9.3

alternatively

through

th9

Thevenin

theorem

ond

,up.rposition.

This,

in4eecl,

is

a

powerful

method

for

large

networks.

9.5

SELECTION

OF

CIRCUIT

BREAKERS

.Iwootthccircuitbrcakcrratingswhiclrrcc;uircthcctrnlptlttttionofSCcurrent

are:

rated

momentary

current

and

rated

symmetrical

interruptirtg

c:nrrent'

Syrnmetrical

SC

current

is

obtained

by

using

subtransient

reactances

for

synchronous

rnachines.

Momcntary

current

irms)

is

then

calculated

by

multiplying

the

symmetrical

-o-"nory

current

by

a

factor

of

1'6

to

account

for

the

presence

of

DC

off-set

current'

Symmetrical

current

to

be

intcrrupted

is

computed

by

r'rsing

subtransient

reactances

tor

synchronous

generators

and

transient

reactances

for

synchronous

motors-induction

motors

are

neglected*.

The

DC

off-set

value

to

be

added

to

obtain

the

current

to

be

interrupted

is

accounted

for

by

multiplying

the

symmetrical

SC

current

by

a

factor

as

tabulated

below:

Multiplying

Factor

,Qrrrnmalrinal E^..t+ A --r. --!-

If

sc

MVA (explained

below)

is

more

than

500,

the

above

multiplyingiactors

are

increased

by

0.1

each.

The

multiplying

factor

for

air

breakers

rated

600

v

or

lower

is

1.25.

The

current

that

a

circuit

breaker

can

intemr

rng

voltage

over

a certain

range,

i.e.

Amperes

at

operating

voltage

Rated

intemrpting

MVA

(three-phase)

capacity

=

'6ty(tifle)lrated

x

11(line)lrated

inremrpting

cunent

where

V(line)

is in

kV

and

1

(line)

is

kA.

Thus,

instead

of_computing

the

sc

current

to

be

intemrpted,

we

cbmpute

three-phase

SC

MVA

to

be

intemrpted,

where

r

--'

'

SC

MVA

(3-phase)

_

Jt

x

prefault

line

voltage

in

kV

x

SC

current

in

kA.

If

voltage

and

current

are

in per

unit

values

on

a three-phase

basis

SC

MVA

(3-phase)

=

lylp,..roul,

x

11116

x (MVA)uur.

(e.r7)

Circuit

Breaker

SPeed

8

cycles

or

slower

5

cycles

3

cyclcs

2

cycles

attempts,

currents

contributed

accounted

for.

1.0

1.1

1.2

1.4

by

induction

motors

during

a

short

Ohviorrslrr rqf oA l\/\/ A i-+^*,--.:- - - -'-'L'Yru'uJrJ'

iciiuu

lvtvA

inieirupiiilg

capaclty

of

a

circuit

breaker

is

to

be

rnurc

thln

(or

cclual

to)

thc

sc

MVA

required

to

be

intemupted.

For

the

selection

of

a

circuit

breaker

for

a particular

location,

we

must

find.

the

maximum

possible

SC

MVA

to

be

intemrpted

with

respect

to

type

and

location

of

fault

and

generating

capacity

(also

synchronous

rnotorl

load)

connected

to

the

system.

A

three-phase

fault

though

rare

is

generally

the

one

which

gives

the

highest

SC

MVA

and

a

circuit

breaker

must

be

capable

of

interrurpting

it.

An

exception

is

an

LG

(line-to-ground)

f.ault

close

to

a

synchronous

generator*.

In

a

simple

system

the

fault

location

which

gives

the

highest

sc

MVA

may

be

obvious

but

in

a

large

system

various

possible

locations

must

be

tried

our

to

obtain

the

highest

st

nava

requiring

Lp"ur"a

SC

computations.

This

is

ilustrated

by

the

examples

that

follow.

Iii"'n"

r.;

I

Three

6.6

kv generators

A,

B

and

c,

each

of

I0o/o

leakage

reactance

and

MVA

ratings

40,

50

and

25,

respectively

are

interconnected

electrically,

as

shown

in

t'In

some

recent

circuit

have

been

tThis

will

be

explained

in

Chapter

1 l.

15:!"'l

.";: I

{d46..t|

Modern

Power

System

Analysis-

T

Fig.

f.i5,

by

a tie

bar

through

curent

timiting

reactors,

each

of

I2Vo

reactance

baiecl

upon

the

rating

ofthe

machine

to

which

it

is

connected.

A

threc-phase

feeder

is

supplied

from

the

bus

bar

of

generator

A

at

a line

voltage

of

6'6

kV'

^f n 1a

Q/phase.

Estimate

the

maximum

MVA

that

can

be

fed

into

a symmetrical

short

circuit

at

the

far

end

of

the

feeder.

currents

can

then

be

calculated

by

the

circuit

model

of

Fig.

g.l6acorresponding

to

Fig.

9.13d.

The

circuit

is

easily

reduced

ro

rhat

of

Fig.

9.16b,

where

7-(0.069

+

j0.138)+

j0.r2s

il

00.15

+

jo.22|

j0.44)

=

0.069

+

j0.226

=

0.236173

SC MVA

=

Volf

=

V"('+')

=

+

pu

(since

Vo

=

1 pu)

\Z)

Z

Fig.

9.15

Sotution

Choose

as

base

50

MVA,

6.6

kV'

Feeder

imPedance

=

%

=(o.o6e+/0.138)pu

Gen

A

reactance

-

o'1[50

=

0.125

Pu

40

Gen

B

reactance

=

0.1

Pu

GenCreactance=0.1

*

4

25

Reactor

A

reactan."

=

o't

''I

tn

40

Reactor

B

reactance

=

0.12

Pu

(MVA)Ba."

=

212

MVA

0.236

Consider

the

4-bus

system

of

Fig.

9.17.

Buses

1

and

2

aregenerator

buses

and

3 and

4

are

load

buses.

The generators

are

rated

l

kv,

100

MVA,

with

transient

reactance

of

l07o

each.

Both

the

transformers

are

1ll110

kV,

100

MVA

with

a

leakage

reactance

of

5Vo.

The

reactances

of

the

lines

to

a

base

of

100

MVA,

110

kv

are

indicated

on

the

figure.

obtain

the

short

circuit

solution

for

a

three-phase

solid

fault

on

bus

4

(load

bus).

Assume

prefault

voltages

to

be

1

pu

and prefault

currents

to

be

zero.

(G)

Fig.

9.17

Four-bus

system

of

Example

g.5

Solution

Changes

in

voltages

and

currents

caused

by

a

short

circuit

can

be

calculated

from

the

circuit

model

of

Fig.

9.18.

Fault

current

1/

is

calculated

by

systematic

network

reduction

as

in

Fig.

9.19,

I

Z

50

Reactor

C

reactance

=

0.12

x 50

=

0.2

pu

=

0.15

pu

-

0.24

pu

(0.069

+i0.138)

(a)

j0.2

j0.12

jo.24

Tie

bar

1

yo

=

1Z0o(

Fig.

9.16

(b)

lo*

!o;E

,^o I Moclern Power Svstem

AnalYsis

I

14

tt

=

-*=

=

-

jt.37463

pu

j0.13s60

t,=

rs x

i:

i3;::

=

-

j3

837or

pu

j0.37638

12=

r, x

{:

i::::

=

-

j3.53

762 pu

-

''

j0.37638

Let us

now

compute

the

voltage

changes

fclr

buses

l,2and

3. From Fig.

9.

l9b,

wc givc

AVr-

0

-

(/0.15)

(-

j3.8370r)

=

-

0.57555 pu

AV,

=

0

-

(iO.l.s) (-

.i3.53762)

=

-

0.53064

pu

Now

jo

1,

),

7

D':

_

jo.2

[0

t,

i0.1

A,

l,zs

2

t,

i,

-t,

10.15

I

I r

-

---rnTl

4+

ib.rs

Izt

\

i

ro'rs

o)

r

-f-

i.0.11

I

t--

-

'AtiA'-

l,

i0

1'':,

,

,t,.(^

.-

t

iots

ll

4T

(

tvl=to

(a)

*

irt

(c)

l''l

I

F'tt

I

2iI06'

)

(rlr

io.t\P

''r),}o'rs

-l

(b)

(.

)vl

=

t.o

ir

fr'

(

,-l

,

-J

10.04166

tt*)

-i

(

)V?

=

1.0

\..

t.

Ill

I

(e)

+

I

,-j

;0.

''

uuuo

l

(

)

v?

=

t.o

Tr

V,'=

l+

lVt=0.4244.5

pu

V),

=l+

AVz=0.46936pu

.

v,J

-vJ

/

l-t

=

,of

tr.o.t

=

J0'17964

pu

AVy=

0

-

[(/0.15)

(-

j3.83701)

+

Q0.15)

(/0.17964)l

=

-

0.54fi(r0

pu

Vtt=

I

-

0.54860

=

0.4514 pu

vlo=

o

The

determination

of

currents

in the

remaining

lines

is left

as an

exercise

to

tltcr

rr'ldcr.

Short circuit

study

is complete

with

the

computation

of

SC

MVA

at bus

4.

(SC

MVA)^

=

7 .37463

x

100

=

737.463

MVA

It is

obvious that

the

heuristic

network

reduction

procedure

adopted

above

is

not practical

for

a real

power

network

of even

moderate

size.

It is,

therefore,

essential

to

adopt

a suitable

algorithm

fbr

carrying

out

short

circuit

study

on

a

digital

computer.

This is

discussed

in

Sec.

9.6.

9.6 ALGORITHM

FOR

SHORT

CIRCUIT

STUDIES

So far

we have

carried

out

short

circuit

calculations

for

simple

systems

whose

llitssivc

ttctworks

can

be

easily

reduced.

In this scction

wc

extcnd

our study

to

Now

Fig.

9.19

Systentatic

reduction

of

the

network

of

Fig'

9'18

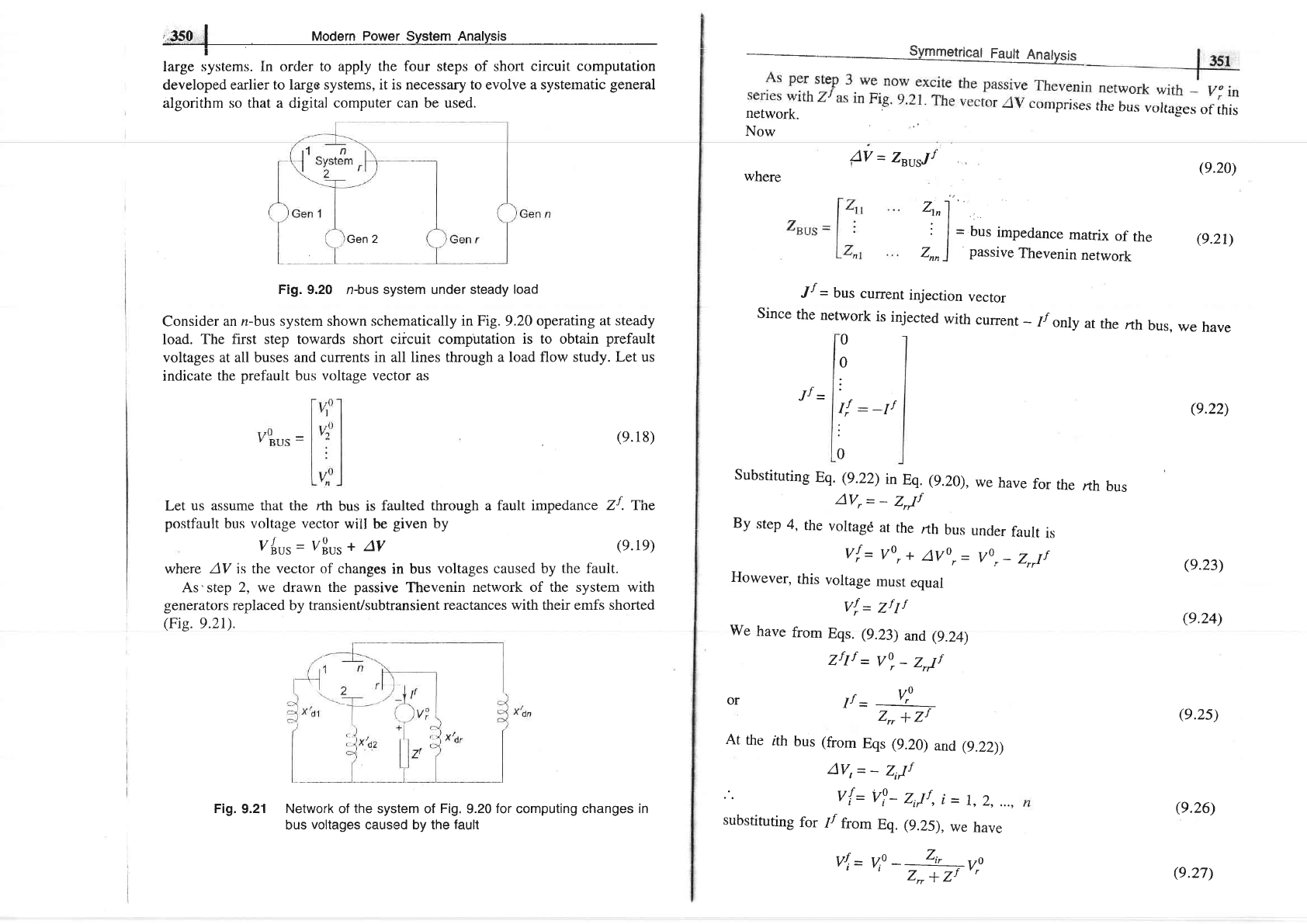
i*.3€0

-l

Modern Power

System

Analysis

large

,tyrt"-r. In orcler to apply the four steps of short

circuit computation

developed earlier

to

large

systems, it is necessary to evolve a systematic

general

algorithm so that a digital computer

can

be used.

Gen 2

Fig. 9.20 n-bus system under steady

load

Consider

an n-bus system shown

schematically in Fig.9.20 operating

at steady

load.

The first step towards short ciicuit computation

is to obtain

prefault

voltages at all buses and

currents in all lines through

a load flow study. Let us

indicate

the

prefault

bus voltage vector as

_

Symmetr.ic-,.....,*",,;al

Fault Anatlrsis

4V

=

Z"urJf

where

.7

-'l

'-

otn

I

i

I

=

bus

impedance

matrix

of

the

e.2D

Znn

)

passive

Thevenin

network

rth

bus

(e.20)

(e.22)

(e.23)

(e.24)

u//

=

bus

current

injection

vector

Since

the

network

is

injected

with

current

-

1/

only

at

the

rth

bus,

we

have

0

Let

us assume that the rth

bus is

faulted

through a fault impedance

Zf . The

postfault bus voltage vector

will be

given

by

V{ur=

VBus

+

AV

:

rf ,f

I,

:

-I'

:

Substituting

Eq. (9.22)

in

Eq.

(g.20),

we

have

for

rhe

AV,

=

-

ZrJf

By

step

4,

the

voltage

at

the

nh

bus

under

fault

is

v!=

vor+

avo,-

vor-

Z,Jf

However,

this

voltage

must

equal

Vd

=

7f

1f

We

have

from

Eqs. (9.23)

and (g.24)

zftf

-

vo,_

z,Jf

or

f=

V:

Zr,

+

Zf

At

the

rth

bus (from

Eqs (9.20)

and (g.22))

AV,

=

-

Z,Jf

v{=

v?-

Z,Jf,

i

=

1,2,

...,

substituting

for

//

from

Eq. (9.25).

we

have

vI=

vf

-

:

zl';rv!

z*+L

/-

(e.18)

(e.1e)

where AV is

the vector of changes

in

bus

voltages caused by

the fault.

As'step

2,

we drawn

the

passive

Thevenin

network of the system with

generators

replaced by transient/subtransient

reactances with their emfs shorted

(Fie.9.21).

Fig.

9.21 Network of

the

system of

Fig.

9.20

for

computing

changes in

bus

voltages

caused by the

fault

(e.2s)

(e.26)

(e.27)

network.

_--.rr.vv\,

rrrv

u(rr

vurraegcs

oI

mls

Now

Fi1.9.22

f",

=

&#;

(prefault generator output

=

Pci

+

iQci)

(9.30)

v,u

E'Gi

=

V,

+

jXt"/t)",

(9'31)

From

the SC

study,

Vf

,is

obtained.

It then

follows

from

Fig.

9.22(b)

that

I rca

Siimmetrica!

Fault

,Analysis

|

-?53

First of all the bus

admittance

matrix

for the network

of

Fig.

9.18

is

formed

as follows:

-r

-

j28.333

352

i

rtllodern

Power

System

Analysis

Fori=rinEq.(9.27)

(e.28)

In the

above

relationship

V,o'r,

the

prefault

bus

voltages

are assumed

to be

known

from

a load

flow

study.

Zuu,

matix of

the short-circuit

study

network

of

Fig. 9.21

can

be

obtained

by

the

inversion

of

its furr5

matrix

as

in Example

9.6

or the

Zru, building

algorithm

presented

in Section

9.7.It

should

be

observed

here that

the

SC study

network

of

Fig. 9.2I

is different

from

the

corresponding

load

flow study

network

by the

fact'that

the shunt

branches

corresponding

to

the

generator reactances

do

not appear

in

the load

flow

study

network.

Further,

in

formulating

the

SC study

network,

the

load

impedances

are

ignored,

these being

very

much

larger

than

the

impedances

of

lines

and

ginerators. Of

course

synchronous

motors

must

be included

in

Zuur

tormula-

tion

for

the SC

study.

Postfault

currents

in

lines

are

given by

f

u=

yu

(vri-

vt)

Q.29)

For

calculation

of

postfault

generator current,

examine

Figs.

9.22(a)

and

(b).

From

the

load flow

study

(Fie.

9.22(a))

Prefault

generator output

=

PGr

+

iQci

-l

Yr.>=Yrt=

_-

175.000

tL Lt

j0.2

-l

Y3=

Yy

=

;r*

-

i6.667

-1

Yrq=

Yq=

J,3.l

=

i10.000

Yzz=

.:-++-+++:^

=-

j28.333

j0.15 j0.1s

"

jj.r j0.2

Yzt=

Yn=

+=

j10.000

j0.1

-l

Yzq=

Yn=

F;

-

i6.667

Y-.=

I

+

I

=-i16.667

'33-

j0.15

'

jo.1

Ytq= Yqt

=

0.000

v

-

I

-

I

Yqq=

,-

*

,.""

--

i76'667

I1

-t-

I

--r

(b)

(a)

By inversion

we

get

Z",tt as

rrc,=tfr!

i

ir;rnr;;.;

I

(e.32)

j0.0s97

j0.0903

j0.0780

jo.o719

j0.0719

j0.0780

j0.13s6

j0.0743

Now, the

postfault

bus

voltages can be obtained using Eq.

(9.27)

as

To

illustrate

the

algorithm

discussed

above,

we shall

recompute

the

short

circuit

solution

for Example

9.5

which was

solved

earlier

using the

network

reduction

technioue.

V{= Vo

-Zto

VP

rrZooa

,2.tr!A | ^/lndarn Pnrrrar Qrratarn Analrrcic

JJ' I

lYlVVVlll

I

Vltvl

Vtvlvlll

,

rlrsrtvre

I

The

prlfault

condition

being

no load, V0r=

Voz=

V03- Voo=

1pu

- r 1.000

,J

-

_

-

2,,{or

Zzz)

malriaal

| |

tglt

tvql

Eat

qu

1.00

j0.0903

=

-

jIL074I97

pu

r.o-

i99199

x

10

=0.4248pu

i

0.1356

vrz= v:

-

?':

r,',

LLzoor

i

0.0710

=

1.0

-

o -

::

x

1.0

=

0.4698

pu

j0.1356

7

v{= v\

-

1*

vf

Zoo

i0.0743

=

1.0

-

'

-

::

_:

1.0

=

0.4521

pu

j0.r3s6

vi

=

o'o

Using Eq.

(9.25)

we can obtain

the

fault current

as

7r=

.r-^0.9^o=-

=,

j7.3j463pu

j0.13s6

These

values

agree

with those

obtained

earlier in

Example 9.5.

Let us

also

calculate

the

short circuit

current

in lines 1-3,

1-2,

l-4,2-4

and

2-3.

,r

v,r

-v{

0.4248-0.4521

[12=

-:-

-

jo'182

Pu

z.n

i0.15

- r

v,r

-v{

0.4248-

0.4698

trrz=

-'_-

'2-:-

_

j0.225

pu

zrz

.i0.2

r r

yr -v{

_

o.4z4v-o

,

t4

-

i4.248

pu

4q

jo'l

. r

u'l

-

v{

0.46e8

-

o

Iiq='-

q

---=

-

j3.132pu

zz+

i0'15

--r

v{

-v^

0.4698

-0.4521

I-Izt=

tiutt

=

TO-

=

-

./0.177 Pu

For the

example on

hand this method

may appear

more involved

compared

to the heuristic

network

reduction

method

employed

in

Example

9.5.

This,

however, is

a systematic

method and

can be

easily adopted

on

the digital

computer

for

practical

networks

of large size.

Further,

another

important

feature

of the method

is that having

computed Zu's,

we can

at once

obtain

all the

required short

circuit

data for a fault on

any bus. For

example,

in

this

particular

system, the

fault

current

for a fault on

bus

I

(or

bus

2)

will be

By Inventing

Y"u"

/nus

=

Yrus Vsus

or

Vsus

=

[Y"ur]-t

/eus

=

Znus /eus

or

Zsvs

=

[Yuur]-t

The

sparsity

of fsu,

may

be retained by

using an efficient inversion

technique

[1]

and

nodal

impedance

matrix can

then be calculated directly

from

the

factorized

admittance

matrix.

This is beyond

the scope of this book.

Current

Iniection

Technique

Equation

(9.33)

can

be

written in the

expanded form

V1

:

211\

*

Ztzlz

1

...

*

ZnIn

v2:22111

+

22212

+... +

zznln

(e.34)

(e.33)

(e.35)

V,

:

Zntll

*

2,,21r

*

.. .+ Z,,nl,,

It

immediately

follows

from

Eq.

(9.34)

that

z

-v'l

"ii

-

Irl,r:

rz

:...:

rn=o

I1-r0

Also

Zi,

-

Ziii

(Znvs

is

a symmetrical

matrix).

As

per

Eq.

(9.35)

if a

unit current

is injected at bus

(node)

7,

while the

other

buses

ere kept

opon

circuited,

the bus

voltages

yield

the

values

of

theTth

column

of

Zuur.

However,

no

organized

computerizable

techniques are

possible

for

finding

the

bus

voltages.

The

technique

had

utility

in AC

Network Analyzers

'where

the bus

voltages

could

be read by

a voltmeter.

Consider

the network

of

Fig. 9.23(a)

with three buses

one of which is a

reference.

Evaluate

Zsus.

Sotution

Inject

a

unit

current

at

bus

I keeping bus

2 open circuit, i.e.,

Ir

=

I.

and

Ir=

0

as in

Fig. 9.22(b).

Calculating

voltages at buses I

and 2,

wehave

Ztt=Vt=7

Zzt=Vz=4

.f

356

|

Modern

Power

System Analysis

Now let It

=

0

and

12

=

1. It similarly

fbllows

that

Ztz=Vt=4=

Zn

Because

of the above

computational procedure,

the Zru,

matrix

is

referred

to as the

'open-circuit

impedance

matrix'.

Z"vs

Building

Algo4ithm

It

is

a step-by-step programmable

technique

which

proceeds

branch

by branch.

It has

the advantage

that any

modification

of the

network

does not require

complcte

rebuilding

of Z"ur.

Consider that Zrur

has been

formulated

upto

a certain stage

and another

branch is

now added. Then

Zrur

(old)

Zo:branch

impedance

Zsus

(new)

Upon adding a new

branch,

one of the

following

situations is

presented.

Fig. 9.23 Current injection

method of

computing Zru.

26 is

added from a new

bus to

the reference

bus

(i.e.

a new branch is

added

and

the

dimension

of

Zry5

goes

up

by one). This is type-I

modificution.

Symmetrical

Fault

Analysis

!,

f5l

,

4r,

the dimension

of Zsu5

goes up by one).

This is

type-2 modification.

3.

Zuconnects

an old

bus

to the

reference branch

(i.e.,

a new loop is

formed

dimension

of 2o,,"

does not change).

This is

type-3 modification.

4. Zuconnects

two

old buses

(i.e.,

new loop

is

formed

but the dimension

of

Zuu, does

not change).

This

rs type-4

rnodittcation.

5.

Zu connects

two

new buses

(Zeus

remains

unaffected

in this

case).

This

situation

can

be avoided

by suitable

numbering of

buses

and from

now

onwards

will be

ignored.

Notation:

i,

j-old

buses;

r-lsfelence

bus; k-new

bus.

Type-

1

Modification

Figure

9.24

shows

a

passive

(linear)

n-bus

network

in

which branch

with

impedance

2,,

is added

to the

new bus

k

and

the

reference

bus r. Now

Hence

V*=

ZJ*

Zri=

Z*

=

0;

i

=

1,2.

....

tt

Zm=

Zu

Fig. 9.24

,

Type-1 modification

Type-2

Modification

Zo is

added

from

new

bus ft to

the old

bus

7

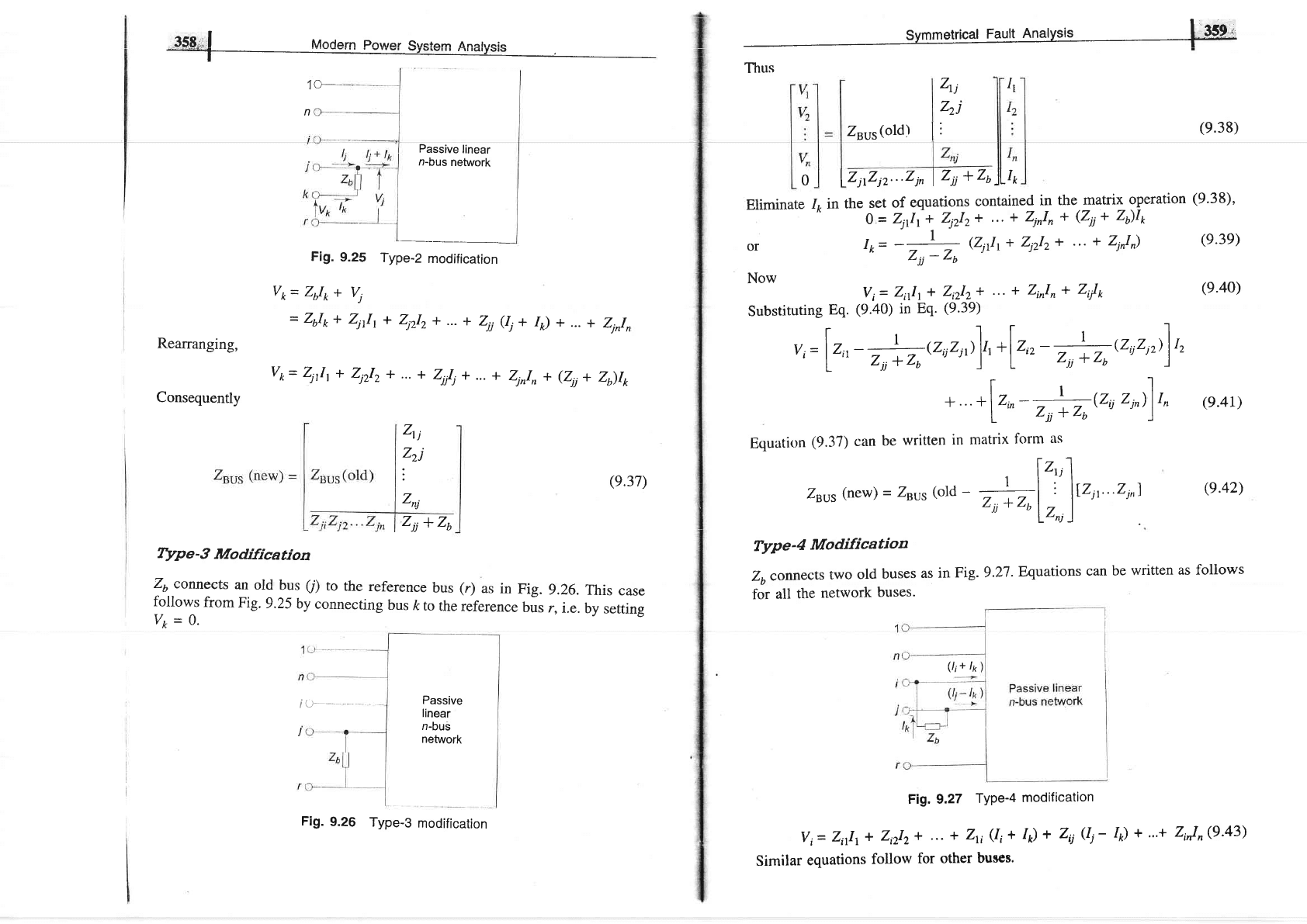
as in Fig. 9.25.It

follows from

this

figure

that

l7

41

Zvus=

l+

6l

s,,"

(old)

Zsvs

(new)

-

(e.36)

t.

Passive

linear

n-bus

network

35S;,1 MorJern Powcr Srrctarn anatrroio

1O_

n

Passive

linear

n-bus

network

Fig.

9.25

Type-Z

modification

Vo=

Zdo

+

V,

=

Zr,I*+

ZiJr+

Zlzlz

+...

+

Zii

ei*

I)

+

...

+

Zinln

Rearranging,

V*=4lt+

Zlzlz

+...

+

2,,1,+...+

Zi,ln+(Zii+

Z)lk

Consequently

Zrj

zzj

Zsvs(old)

I

:

(e.38)

o

I lzyziz...zi,

I

zii

+

z,

)lI*

lr

Eriminate

{

in

the

3":';,,iiy';;;?::"i"t

i.I"

a;y>;i:ation

(e'

3

I

)'

1

or

'o=

-12

(\1Ir+

Zi2Iz+

"'

+ ZlnI)

(9'39)

Now

V;=

2;111+

Z,rI,

+

"'

+ Z'nIn

+

Z;/r

(e.40)

(e.42)

Zti

Zzj

:

Znj

(e.37)

Substituting

Eq.

(9.40) in

Eq.

(9.39)

,,

=

lr^

-

h(z*

1

rr]a

*

lr,,

-

"h

rz

uz,,>)r,

+

lr^-

^i{zu

2,,1)r,

(s.4t)

Equation

(9.37) can

be

written

in matrix

form

as

. |t"f

ZsLr5

(new)

=

znvs(old

-

;+;l

:

ltz't"Zv)

"jjT"ulz,,

l

zjj

+

zb

IYpe-3

Modification

zu

connects

an

old

bus

(l)

to

the

reference

bus

(r)

as

in

Fig.

9.26.

This

case

follows

from

Fig.9.25

by

connecting

bus

ft

to

the

reference

bus

r,

i.e.

by

setting

v*=o'

Type-

Modification

zo

connects

two

old

buses

as

in

Fig. 9.27

. Equations

can

be

written

as follows

for

all

the

network

buses.

Fig. 9.27

TYPe-4

modification

Vi=

Z;11,

+

Z,lr+

"'

+

Zri

(Ii

+ /)

+

ZU

Qi-

Similar

equations

follow

for

other

buses.

J

Passive

linear

n-buS

network

(l;+ lp

Fig.

9.26

Type-3

modification

/o)

+ ...+

ZiJ"(9.43)

360

|

Modern

power

System

Analysis

I he voltages

of the

buses

i and

j

are,

however,

constrained

by

the

equation

(Fig.

9.27)

Symmetrical

Fault

Analysis

I

fOt

Step

I: Add

branch

2,,

-

0.25

(from

bus

I

(new)

to

bus

r)

Step

ZBUS

=

t}.25l

(i)

Add

branch

Zzt

=

0.1

(from

bus

2

(new)

to bus

I

(old));

type-Z

V,=

Z,rlo+

Vi

or 21111

+

\212+

...

+

Zit

(1,+

I)*

Zii

(Ii-

I) + ...

+

(e.44)

zi,In

=

Ztl*+

Z,rl,

+

Z,rl"

+

...

+

ZlU,+

I

earTangtng

_I

0

=(Zit-

21)

Ir+ ...

+

(Zti-

Z)

Ii+

eu-

Z)

Ii

+...+

(Z*

-

21,)

In +

(Zu

*

Zii *

Zii

-

Zi

-

Z)

11,

e.45)

Collecting

equations

similar

to

Eq.

(9.43)

and

Eq.

(9.45)

we

can

write

vl

V

vn

0

(9.46)

Eliminating

1o

in

Eq.

(9.46)

on lines

similar

to whar

was

done

modification,

it follows

that

l'"

lZ,,

with

the

use of

fbur

relarionships

Eqs

(9.36),

(9.37),

(9.42)

and

(9.47)

bus

impedance

matrix

can

be

built

by a

step-by-step

procedure

(bringing

in

one

branch

at

a tinle)

as illtrstratc'tl

in lixrrrnple

9.8.

This

pror.cdrrr-c

-hcing

a

mechanical

one

can

be

easily

computerized.

When

the

network

undergoes

changes,

the

modiflcation

proceclures

can

be

cttrployccl

to rcvisc

thc

bLrs

irtrpcdance

rnatrix

ul'thc

nctwol'k.

Thc

opeling

o1

a

line

(Ztt)

is equivalent

to

adding

a branch

in

parallel

to it

with

impedance

-

2,,

(see

Example

9.8).

j Example

9.8

For

the

3-bus

network

I

!,--

0.25

l,'

(--

I

l

I

Ref bus

r

Fig.

9.28

zsvs=',lZ:11,

31i]

(ii)

Step

3: Add

branch

,rt

=

0.1

(from

bus 3

(new)

to bus I

(old));

type-Z

modification

lo.2s

o.zs

0.2s1

zsvs

=

|

o.zs

o.3s

o.2s

|

(iii)

lo.2s

0.2s

0.3s..l

Step

4: Add

branch

zz,

(from

bus

2

(old)

to

bus

r); type-3

modification

10.2s

o.zs

0.25'l

[0.25-l

Zet)s

=

|

o.zs

0.3s

0.2s

| |

o.ts

I to.zs

0.3s

0.251

Lo.2s

o.2s

o3sl

o'3s

+

o

"

Ln.trj

[0.14s8

0.1042

0.14s8-l

=

I

o.ro+z

o.r4s8

o.lo42

|

fo.tott

o.ro42

o.24s8l

Step

5:

Acld

branch

iz-r

=

0.1

(from

bus

2

(olct)

to brrs 31old)):

type-4

modification

[o.l4s8

0.1042

0.l4s8l

zsvs

=

l

o.'oo,

0.1458

o.to42l-

|

0.1

+

0.1458

+

0.2458-2xO.lO42

10.l4s8

O.tO42

0.24s8

)

[-0

1042.l

=

I

0.0417

|

[-o.to+z

0.0411

-0.0417]

[-o.o+tz-l

lo.r3e7

0.1103

0.12501

=

|

0.1ro3

o.I3e7

0.1250

I

|

0.1250

0.17sol

Oltenirtg

o

tinu

(line

3-2):

This is

equivalent

to connecting

an intpeclance

-

0.I

between

bus 3

(old)

and

bus

2

(old)

i.e.

type-4

modification.

Zsus=

Zuur(olcl)

-

(-01)+ol?5

#

Z131,s

(new) =

Zsuts

(old)

-

lzit

-

z1t)

...

(zi,

-

zi))

zb+zii*Zii-zzij

Zsus

I

i,J

o r.

I

shown

in

Fig.

9.28

build

r

9l z

I

'irl

l

L-,

tr

ili

-,

--

6"11-.

I

0.1

3

o.t

filf.lid,

Modern Power

System

Anatysis

-r-r-^r r^..tr Ana*raio

ffir

:)ymmelrlual

raull

rurqryo's

r**

Now

I

-

|

0.1042

0.14s8

0.1042l;

(same

as in

step

4)

0.1458

0.1042

0.2458

|

For

the

power

system

shown

in

Fig.

9.29 the pu

reactances

are

shown

therein.

For

a

solid

3-phase

fault

on bus

3,

calculate

the

following

(a)

Fault

current

(b)

V\ and

vt

(c)

It,r,

I'\,

uxl

Il,

(d)

1fr,

and If,

Assume

prefault

voltage

to be I pu.

0.2

0-.09

1

and

il=(FZE-)=0.286'i2-[^

zu)

These

two

voltages

are

equal

because

of

the

symmetry

of

the

given

power

network

(c)

From

Eq.

(9.29)

and

But

|ffr

Jt

-

or

1f

-

(b)

As

per

Eq.

(9.26)

rr.f

-

v

i-

\,

//

o

''

\

,/'0.,

\/

\..

,/

.,

ll

3'

'

Fig.

9.29

[

0.0147-l

tl

|

-0.0147

|

10.0147

-

0.0147

0.0s001

L

o.osoo_J

(d)

Iri

=

Y,j

(vl

-

vl)

Irtz=

+(0.286

-

0.286;

=

g

j0.1

'

I\t=t|t=

fr

ro.186-o)

-

i2.86

As

per Eq.

(9.32)

, r

E'

or-vrf

r

Gr

-

ixtic

+

ixr

E'Gr

=

1

Pu

(Prefault

no

load)

JI-

F

0.1

c)

|

i-,,

IL.=

1-0'286--

=-

j2'86

Gt-

io.2+io.os

SimilarlY

Ifcz=

i2.86

Solution

The

Thevenin

passive

network

for

this

system

is

drawn

in

Fig.

9.28

with

its

Zru, given

in Eq.

(iv)

of

Example

9.8.

(a)

As

per

Eq.

(9.25)

PROB

LE

M

S

A

transmission

line

of

inductance

0.1

H

ancl

resistance

5 ohms

is

suddenly

short

circuited

at

t

=0

at

the

bar

end

as

shown

in

Fig'

P-9'1'

Write

the

expression

for

short

circuit

current

i(r).

Find

approximately

the

value

of

the

first

current

maximum

(maximum

momentary

current)'

[Hint:

Assume

that

the

first

current

ntaximum

occurs

at the

same

time as

the

first

current

maximum

of

the

symmgtricl.:non

ttrcuit

current')

V:

2,,

+

Zl

Yo-:._1--

--

js.jl

zn

j0.175

vl

-

--Zt--yu

'

zrr+zl'r

9.1

Kothari D.P., Nagrath I.J. Modern Power Systems Analysis

Подождите немного. Документ загружается.