Кузьмин С.И. Методы научных исследований в технических задачах

171

ожидания

kМ

X

.

r

, то относительная ошибка

Δ

v

в оценке мате-

матического ожидания оригинала

kН

X

.

r

определится интерва-

лом:

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

Δ−

−≥Δ≥

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

Δ+

−

−− 11

1

kjkj

aa

v

. (7.35)

Выход за границы интервала связан с вероятностью

)1( h−

.

При исследовании моделей реальных систем признание

того факта, что математическое ожидание величины в натуре

kН

X

.

v

находится внутри интервала

(

)

max

.

min

. kНkН

XX

&&&&&&

−

, не только

вносит неопределенность в принятие решения по ее конкрет-

ной величине, но и может повлиять на выводы, связанные с

характеристиками исследуемого объекта. Так, например,

принимая, что

min

.. kНkН

XX

&&&

v

=

, а фактически может выполняться

другое равенство

max

.. kНkН

XX

&&&

v

=

, то результаты в натуральной

системе будут превышать достоверные на величину погреш-

ности в оценке математического ожидания этой же величины

на модели:

1

min

.

min

.

max

.

−

⎟

⎠

⎞

⎜

⎝

⎛

Δ−

Δ+

=

−

ki

a

kН

kНkН

X

XX

&&&

&&&&&&

,

или в противном случае (гипотеза:

max

.. kНkН

XX

&&&

v

=

, а факт -

min

.. kНkН

XX

&&&

v

=

) результаты могут оказаться заниженными на ту

же величину:

1

max

.

max

.

min

.

−

⎟

⎠

⎞

⎜

⎝

⎛

Δ+

Δ−

=

−

ki

a

kН

kНkН

X

XX

&&&

&&&&&&

.

Поэтому наиболее сложным и неопределенным вопро-

сом при моделировании стохастических систем является

обоснование предельной погрешности, которую можно до-

пустить в конечном результате. Одним из способов такого

172

обоснования может являться требование о предельной по-

грешности при некотором заданном значении вероятности

подобия.

Обозначив требуемую вероятность подобия через

*

h

, а

предельную погрешность подобия

Δ

для некоррелированных

индикаторов подобия предлагается соотношение [15]:

()

∏

∑

=

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

Δ

=

m

j

l

i

iij

m

Xa

p

Фh

1

5,0

1

22

*

2

ω

, (7.36)

Равенство (7.36) решается относительно необходимого

числа моделей

p

методом подбора.

Учитывая вероятность снижения надежности моделиро-

вания вследствие случайности значений коэффициентов ва-

риации

()

iМ

X

.

ω

, рекомендуется принимать для расчетов заве-

домо завышенное значение вероятности подобия

h

hh Λ+=

*

,

где

h

Λ

- некоторая абсолютная погрешность в оценке значе-

ния

*

h

, которая не будет превышена с вероятностью

α

.

Допускаемая относительная погрешность

h

λ

определя-

ется из отношения:

*

h

Λ

=

λ

.

Относительная погрешность системы (общая)

h

λ

нахо-

дится как результирующая относительных погрешностей от-

дельных индикаторов подобия

hi

λ

. Например для

=m

2:

2121 hhhhh

λ

+

+≤

. (7.37)

В этом выражении погрешности

hi

λ

приходится зада-

вать, причем достаточно произвольно, лишь бы удовлетво-

173

рить необходимое условие. Абсолютная погрешность

−

j

го

индикатора определится по выражению:

jhhj

h

λ

=

Λ

,

а, затем по

(

)

j

Ф

δ

- распределению находится значение ошиб-

ки

jН .

δ

при нижней оценки надежности

(

)

hjjМjН

hh

λ

−

=

1

..

. Та-

ким образом можно получить два значения

j

δ

: одно соответ-

ствует

j

h

, а другое

jН .

δ

- значению

jН

h

.

. И приемлемая отно-

сительная погрешность величины

j

δ

составит:

Mj

НjМj

δ

λ

δ

−

=

.

Предельное значение относительной погрешности

S

&&&

λ

выборочного среднего квадратичного отклонения

(

)

j

IS

&&&

δ

λ

−

=

1

S

&&&

Предельная относительная погрешность для коэффици-

ента вариации

()

i

X

ω

определяется с учетом числа моделей

p

:

()

11 −

⎟

⎠

⎞

⎜

⎝

⎛

+=

∧

i

S

X

a

p

i

&&&

λ

ω

. (7.38)

Предельные относительные погрешности для генераль-

ных среднего

μ

и среднеквадратичного отклонения

σ

связа-

ны между собой формулой:

()

μμωσ

λλλλ

−−=

∧

1

i

X

. (7.39)

С другой стороны по выборки объема

n

из нормально

распределенной совокупности относительные погрешности

генерального среднего оцениваются через распределение

Стьюдента

()

α

,1−n

t

при доверительной вероятности

α

:

(

)

()

αμ

ω

λ

,1−

≤

n

t

n

X

,

174

а генерального среднеквадратичного отклонения через рас-

пределение Пирсона -

()

2

1,1

−− n

α

χ

:

(

)

()

1

2

1,1

−

≤

−− n

n

α

σ

χ

λ

.

Принимая соответствующие значения

μ

λ

и

σ

λ

(в преде-

лах ограниченных (7.39)), подбором находится объем выбор-

ки, достаточный для обеспечения заданной надежности мо-

делирования.

В целом, обеспечение условий моделирования стохас-

тических систем может быть сведено к следующим положе-

ниям [15].

1. Определяется необходимое количество моделей

p

,

обеспечивающих заданную надежность моделирования

h

при доверительной вероятности

α

. Определяется расчетная

надежность моделирования (погрешность подобия вероятно-

сти)

*

h

.

2. Вычисляется относительная погрешность моделиро-

вания:

*

h

hh

h

−

=

λ

2.

Если критериев подобия больше двух

2≥

I

, то полу-

ченное значение

h

λ

распределяется между ними на

основе соотношения (7.37):

∑∑∑

<<

=

<

++=

kji

hkhjhi

mj

ji

hjhi

m

i

hih

λλλλλλλ

*.....*

Распределение погрешностей

hkhi

λ

,...,

рекомендуется

проводить пропорционально дисперсиям критериев

(

)

(

)

ki

ISIS

&&&&&&

22

,.....,

.

175

3. Для каждого критерия проводится анализ на опреде-

ление количества образцов необходимых для вычисления

средних и среднеквадратичных ошибок параметра

j

X

.

3.1. Анализ начинается с критерия, у которого наи-

большее значение

hj

λ

. С помощью распределения Лапласа

Ф

абсолютные ошибки в моделирования для модели

М

δ

и на-

турального объекта

Н

δ

:

⎟

⎠

⎞

⎜

⎝

⎛

=→

−

2

1

Мj

МjМj

h

Фh

δ

⎟

⎠

⎞

⎜

⎝

⎛

=→

−

2

1

Нj

НjНj

h

Фh

δ

Надежность моделирования натуры

Нj

h

определяется по

формуле:

(

)

MjhjНj

hh

λ

−

=

1

3.2. Вычисляется относительная ошибка (погрешность)

абсолютного отклонения

j

δ

λ

:

Mj

НjMj

j

δ

λ

δ

−

=

.

3.3. Определяется предельная относительная погреш-

ность коэффициента вариации физической величины (подле-

жащей изучению на статистические характеристики) в моде-

ли

()

X

ω

по формуле (7.38):

()

11 −

⎟

⎠

⎞

⎜

⎝

⎛

+=

∧

i

jS

Xj

a

p

&&&

λ

ω

j

jS

δ

λ

−

=

1

&&&

3.4. Находится относительная погрешность генерально-

го среднего

j

μ

λ

:

()

∧

=

Xjj

b

ωμ

λλ

,

176

и генерального среднеквадратичного отклонения

j

σ

λ

:

()

(

)

jjXjj

μμωσ

λλλλ

−−=

∧

1

где

b

- коэффициент, подбираемый опытным путем из сооб-

ражения равенства числа образцов, необходимых для оценки

генерального среднего

μ

и генерального среднеквадратично-

го отклонения

σ

. Рекомендуемые значения

(

)

1,005,0 −

=

b

.

3.5. Исходя из предположения о нормальном распреде-

лении параметров в выборке объема

n

, последовательно на-

ходится количество образцов для оценки генерального сред-

него

μ

n

и генерального среднеквадратичного

σ

n

:

()

j

n

j

n

t

X

μ

α

μ

ω

λ

→=

−1,

(

)

()

j

n

j

n

σ

α

σ

χ

λ

→−

−

=

−−

1

2

1,1

Пример. Методику оценки точности моделирования

технической системы рассмотрим на примере исследования

деформации пространственной строительной конструкции

при воздействии сосредоточенных нагрузок

P

.

Условие подобия при воздействии на конструкцию со-

средоточенными усилиями выражается одним безразмерным

комплексом (индикатором подобия):

1

21

==

−−

МММ

ННН

LEР

C

rr

r

σ

(7.40)

где

E

- модуль упругости материла, Па;

L

- характерный линейный размер.

Интервальная оценка для напряжений

σ

и перемеще-

ний

u

в натуральном объекте по соответствующим характе-

ристикам модели определится в соответствие с (7.34):

σσ

σσσ

СС

МНМ

v

&&&

v

&&&

Δ−

<<

Δ+ 1

1

177

LМНLМ

СuuСu

v

&&&

v

&&&

5,05,0

1

⎟

⎠

⎞

⎜

⎝

⎛

Δ−

<<

⎟

⎠

⎞

⎜

⎝

⎛

Δ+

(7.41)

Среднее арифметическое значение модуля упругости

М

E

определено экспериментально, результаты приведены в

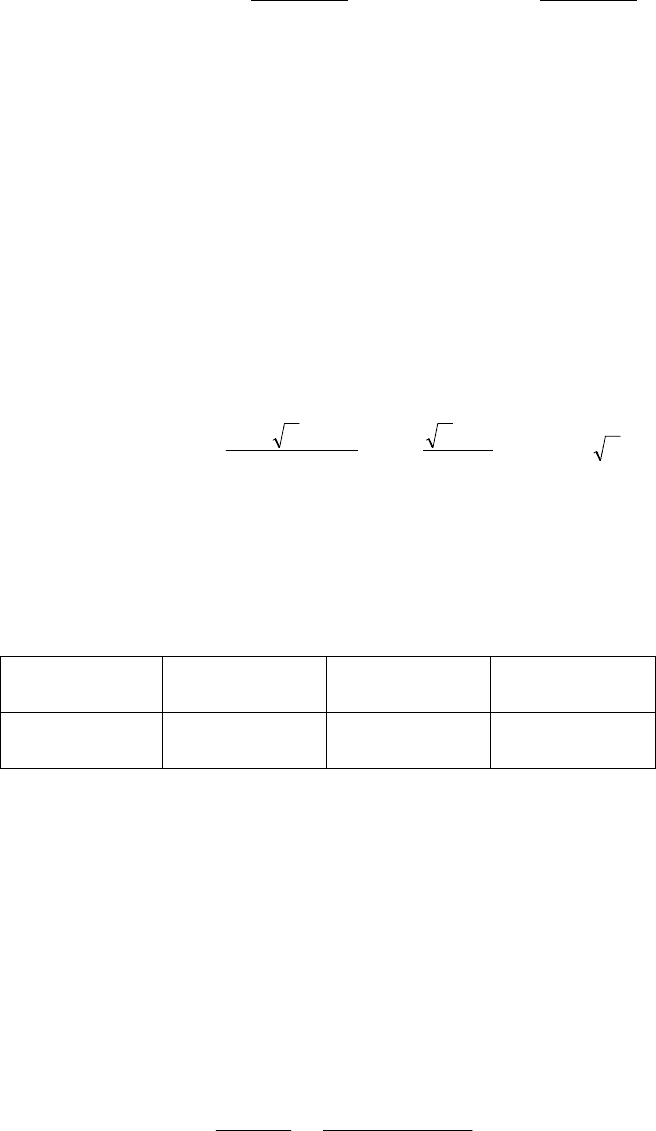
таблице.

Таблица

Коэффициент вариации модуля упругости для нату-

рального образца находится по формуле:

()

[

]

(

)

ММEH

ЕE

ω

λ

ω

.

1

+

=

Относительная погрешность коэффициента вариации

модели

()

ME.

ω

λ

определится через соответствующие статисти-

ческие оценки при доверительной вероятности

95,0=

α

и

числе степеней свободы

)15(

−

=

f

:

()

474,1

042,01

042,037,1

1

.

=

−

+

=

−

+

=

E

ME

r

v

λ

σ

ω

()

042,078,2

5

034,0

5

)1(

===

−

α

ω

λ

t

E

M

E

v

()

37,11

71,0

4

1

2

=−=−=

α

σ

χ

λ

f

E

Возможная погрешность в оценке коэффициента вариа-

ции модуля упругости натурального объекта составит:

Значение параметра в опыте

Параметр

1 2 3 4 5

Модуль упругости модели,

КПа

334 356 362 347 338

Среднее значение модуля

упругости, КПа

347

Дисперсия воспроизво-

димости

2

.

Eвоспр

S Па

2

,

138800000

Среднеквадратичная

ошибка

()

M

ES , Па

11781

Коэффициент вариации

модуля упругости

()

M

E

ω

0,034

178

()

[

]

084,0034,0*474,11

=

+

=

H

E

ω

Среднеквадратичное отклонение

(

)

IS

индикатора

σ

C

составит:

() ( ) ( ) ()

[]

[

]

093,002,0*4084,004

5,0

22

5,0

222

=++=++= LEPIS

ωωω

Предельная допустимая погрешность индикатора подо-

бия

Δ

определится в предположении о нормальном распре-

делении

E

и

L

по формуле:

182,0093,0*96,1

2

1

==

⎟

⎠

⎞

⎜

⎝

⎛

=Δ

−

S

h

Ф

Где

1−

Ф

обратная функция Лапласа при

95,0

=

h

.

Тогда интервалы для напряжений

Н

σ

и перемещений

Н

u

натурального объекта составят:

σσσσ

σσσσσσ

СССС

МНММНМ

v

&&&

v

&&&

v

&&&

v

&&&

222,1846,0

182,01

1

182,01

1

<<=

−

<<

+

LМНLМLМНLМ

СuСuСuСu

v

&&&

v

&&&

v

&&&

v

&&&

105,1920,0

1

5,05,0

<<=

⎟

⎠

⎞

⎜

⎝

⎛

Δ−

<<

⎟

⎠

⎞

⎜

⎝

⎛

Δ+

σσ

Таким образом, с надежностью 95% можно предполо-

жить, что погрешность в оценке напряжений не превышает

(+16,4%) и (-22,2%), а для перемещений соответственно

(+8%) и (-10,5%).

Задача определения числа моделей при моделировании

математического ожидания натурального объекта решается

исходя из назначаемых величин погрешности моделирования

Δ

и требуемого уровня доверительной вероятности подобия

h

.

Примем уровень вероятности подобия

95,0

=

h

, а пре-

дельную погрешность результатов оценки напряжений для

натурального объекта

H.

σ

Δ

не более

%10

±

. Так как в приня-

той системе имеется только один индикатор подобия (7.35),

179

следовательно

1=

kj

α

, и по (*) найдется \погрешность оценки

напряжений для модели:

MM

H

jk

..

.

1

11,0

1

.

σ

α

σ

Δ−

−=−=

⎟

⎠

⎞

⎜

⎝

⎛

Δ−

−=Δ−

−

;

09,0

.

=

Δ

M

σ

Среднеквадратичное отклонение индикатора модели со-

ставит:

() ( ) ( ) ()

[]

[

]

052,002,0*4034,004

5,0

22

5,0

222

=++=++= LEPIS

ωωω

По формуле () при

M.

σ

Δ

=

Δ

и найденном значении

()

IS

определяется

()

[]

()

pФ

IS

p

Ф

Xa

p

Фh

M

m

j

l

i

iij

m

731,1222

5,0

2

.

1

5,0

1

22

*

=

⎟

⎠

⎞

⎜

⎝

⎛

Δ

=

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

Δ

=

∏

∑

=

σ

ω

Значения

*

h при различных количествах испытываемых

моделей

p

представлены в таблице.

Таблица

p

1 2 3

h

0,916 0,986 0,997

Таким образом, уже при

p

=2, расчетная надежность мо-

делирования превышает заданное значение:

95,0986,0

*

>=h

.

Объем выборки для определения коэффициента вариа-

ции модуля упругости в модели

(

)

(

)

Mi

EX

22

ωω

= , определяется

по изложенному выше алгоритму.

Относительная погрешность моделирования:

0365,0

986,0

95,0986,0

*

=

−

=

−

=

h

hh

h

λ

Абсолютные ошибки в моделирования для модели

М

δ

и

натурального объекта

Н

δ

:

180

46,2

2

986,0

2

11

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=→

−−

Ф

h

Фh

Mj

MjMj

δ

96,1

2

95,0

2

11

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=→

−−

Ф

h

Фh

Нj

НjНj

δ

Надежность моделирования натуры

Нj

h

:

(

)

(

)

95,0986,0*0365,011

=

−

=

−=

MjhjНj

hh

λ

Относительная ошибка (погрешность) абсолютного от-

клонения

j.

δ

λ

:

203,0

46,2

96,146,2

.

=

−

=

−

=

Mj

НjMj

j

δ

λ

δ

,

и относительная погрешность коэффициента вариации

модуля упругости модели

(

)

M

E

ω

-

()

∧

Eм

ω

λ

:

()

7748,01

1

255,0

1211 =−

⎟

⎠

⎞

⎜

⎝

⎛

+=−

⎟

⎠

⎞

⎜

⎝

⎛

+=

∧

i

jS

Eм

a

p

&&&

λ

ω

255,0

203,01

203,0

1

=

−

=

−

=

j

jS

δ

λ

&&&

Принимая

05,0=b

, находится относительная погреш-

ность генерального среднего

j

μ

λ

:

()

0387,07748,0*05,0 ===

∧

Eмj

b

ωμ

λλ

и генерального среднеквадратичного отклонения

j

σ

λ

:

()

(

)

(

)

706,00387,00387,017748,01 =−−=−−=

∧

jjXjj

μμωσ

λλλλ

Далее находится количество образцов для оценки генераль-

ного среднего

μ

n

и генерального среднеквадратичного

σ

n

:

()

11,1

034,0

0387,0

1,95,0

===

−

μ

ω

λ

n

t

E

n

M

j

5

=

μ

n

Кузьмин С.И. Методы научных исследований в технических задачах

Подождите немного. Документ загружается.