Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

NAP-SVM

The main goal of the SVM Nuisance Attribute Projec-

tion (NAP) method is to reduce the impact of channel

variations (called also session variability). It uses an

appropriate projection matrix P in the SVM super-

vector space (a supervector is obtained by concatenat-

ing the Gaussian means) to remove the subspace that

contains the session variability.

¼ P  s; ð1Þ

where, s is a GMM supervector. The projection matrix

can be written as follow:

P ¼ðI  VV

Þ; ð2Þ

where, V ¼½v

; :::; v

 is a rectangular matrix of

low rank whose columns are orthonormal. The vec-

tors v

are obtained from the k eigenvectors having

the k largest eigenvalues of the following covariance

matrix:

s ¼1

i¼1







Þð







ð3Þ

where



represents the GMM supervector of the ith

session of the sth speaker. S is the number of speaker in

V -Matrix training data. n

is the number of different

sessions belonging to the sth speaker.



is the mean

GMM supervector obtained overall the sessions be-

longing to the sth speaker:



i¼1



: ð4Þ

▶ Session Effects on Speaker Modeling

National Institute for Standards and

Technology

▶ Fingerprint, Forensic Evidence of

Natural Gradient

When a parameter space has a certain underlying

structure, the ordinary gradient (partial derivative) of

a function does not represent its steepest direction.

Riemannian space is a curved manifold where, there is

no orthonormal linear coordinates. The steepest descent

direction in a Riemannian space is given by the ordinary

gradient pre-multiplied by the inverse of Riemannian

metric. Such direction is referred to as natural gradient.

▶ Independent Component Analysis

Near Field Communication

Synonym

NFC

Definition

A method of wireless communication that uses mag-

netic ﬁeld induction to send data over very short dis-

tances (less than 20 cm). NFC is intended primarily

for deployment in mobile handsets.

▶ Transportable Asset Protection

2009 Springer Science+Business Media, LLC

Near Infrared (NIR)

Electromagnetic radiation, identical to visible light, ex-

cept at wavelengths longer than red light; the near infra-

red band (IR-A) extends from 700 to 1,400 nm, while

the whole infrared region ranges from 700 to 3,000 nm.

▶ Face Recognition, Near-infrared

▶ Finger Vein

▶ Iris Databases

▶ Iris Device

▶ Palm Vein

Near-infrared Image Based Face

Recognition

▶ Face Recognition, Near-Infrared

NEXUS

▶ Iris Recognition at Airports and Border-Crossings

NIST SREs (Speaker Recognition

Evaluations)

Evaluations of speaker recognition systems coordina-

ted by the National Institute of Standards and Tech-

nology (NIST) in Gaithersburg, MD, USA, 1996–2008.

▶ Speaker Databases and Evaluation

Noisy Iris Challenge Evaluation –

Part I (NICE.I)

The Noisy Iris Challenge Evaluation – Part I (NICE.I)

began in 2007 by the University of Beira Interior.

The NICE.I contest focuse s on the development of

new iris segmentation and noise detection techniques

unlike similar contest which focus more on iris

recognition performance. The iris database used for

the contest, UBIRIS.v2, consists of very noisy iris

images to simulate less constraining image capturing

conditions.

▶ Iris Databases

Nominal Identity

Nominal identity represents the name and in certain

cases the other abstract concepts associated with

a given indiv idual (e.g . the Senator, the Principal,

the actor). Such an identity is malleable and distin-

guished from the less mutable biometric identity,

which is typically predicated on physiological or

behavioral characteristics that do not change much

over time.

▶ Fraud Reduction, Applications

Non-ideal Iris

Non-ideal iris is deﬁned as dealing with off-angle,

occluded, blurred, noisy images of iris.

▶ Iris Image Quality

Non-linear Dimension Reduction

Methods

▶ Non-linear Techniques for Dimension Reduction

1002

Near Infrared (NIR)

Non-linear Techniques for

Dimension Reduction

JIAN YANG,ZHONG JIN,JINGYU YANG

School of Computer Science and Technology, Nanjing

University of Science and Technology, Nanjing, Peoples

Republic of China

Synonyms

Non-linear dimension reduction methods

Definition

Dimension reduction refers to the problem of con-

structing a meaningful low-dimensional representation

of high-dimensional data. A dimension reduction tech-

nique is generally associated with a map from a high-

dimensional input space to a low-dimensional output

space. If the associated map is non-linear, the dimen-

sion reduction technique is known as a non-linear

dimension reduction technique.

Introduction

Dimension reduction is the construction of a

meaningful low-dimensional representation of high-

dimensional data. Since there are large volumes

of high-dimensional data (such as climate patterns,

stellar spectra, or gene distributions) in numerous

real-world applications, dimension reduction is a fun-

damental problem in many scientiﬁc ﬁelds. From the

perspective of pattern recognition, dimension reduc-

tion is an effective means of avoiding the ‘‘curse

of dimensionality’’ and improving the computational

efﬁciency of pattern matching.

Researchers have developed many useful dimension

reduction techniques. These techniques can be broadly

categorized into two classes: linear and no n-linear.

Linear dimension reduction seeks to ﬁnd a meaningful

low-dimensional subspace in a high-dimensional

input space. This subspace can provide a compact

representation of high-dimensional data when the

structure of data embedded in the input space is linear.

The principal component analysis (PCA) and Fisher

linear discriminant analysis (LDA or FLD) are two

well-known linear subspace learning methods which

have been extensively used in pattern recognition and

computer vision areas and are the most popular tech-

niques for face recognition and other biometrics.

Linear models, however, may fail to discover essen-

tial data structures that are non-linear. A number of

non-linear dimension reduction techniques have been

developed to address this problem, with two in partic-

ular attracting wide attention:

▶ kernel-based techni-

ques and

▶ manifold learning related techniques. The

basic idea of kernel-based techniques is to implicitly

map observed patterns into potentially much higher

dimensional feature vectors by using non-linear

mapping determined by a kernel. This makes it possi-

ble for the non-linear structure of data in observation

space to become linear in feature space, allowing the

use of linear techniques to deal with the data. The

representative techniques are kernel principal compo-

nent analysis (KPCA) [1] and kerne l Fisher discrimi-

nant analysis (KFD) [2, 3]. Both have proven to be

effective in many real-world applications.

In contrast with kernel-based techniques, the mo-

tivation of manifold learning is straightforward, as it

seeks to directly ﬁnd the intrinsic low-dimensional

non-linear data structures hidden in observation

space. Over the past few years many manifold learning

algorithms for discovering intrinsic low-dimensional

embedding of data have been proposed. Among

the most well-known are isometric feature mapping

(ISOMAP) [4], local linear embedding (LLE) [5],

and Laplacian Eigenmap [6]. Some experiments

demonstrated that these methods can ﬁnd perceptually

meaningful embeddings for face or digit images. They

also yielded impressive results on other artiﬁcial and

real-world data sets. Recently, Yan et al. [7] proposed a

general dimension reduction framework called graph

embedding. LLE, ISOMAP, and Laplacian Eigenmap

can all be reformulated as a uniﬁed model in this

framework.

Kernel-Based Non-Linear Dimension

Reduction Techniques

Over the last 10 years, kernel-based dimension reduc-

tion techniques, represented by kernel principal compo-

nent analysis (KPCA), and kernel Fisher discriminant

analysis (KFD), have been extensively applied to

biometrics and have been proved to be effective. The

basic idea of KPCA and KFD is as follows.

Non-linear Techniques for Dimension Reduction

1003

By virtue of a non-linear mapping F, the input data

space R

is mapped into the feature space H

F: R

! H

x 7! F xðÞ

ð1Þ

As a result, a pattern in the original input space R

mapped into a potentially much higher dimensional

feature vector in the feature space H

. KPCA is to per-

form PCA in the feature space, while KFD is to perform

LDA in such a space.

This description reveals the essence of the KPCA

and KFD methods, but it does not suggest an effective

way to implement these two methods, because the

direct operation in the high-dimensional or possibly

inﬁnite-dimensional feature space is computationally

so intensive or even becomes impossible. Fortunately,

kernel tricks can be introduced to address this prob-

lem. The algorithms of KPCA and KFD can be imple-

mented in the input space by virtue of kernel tricks. An

explicit non-linear map and any operation in the fea-

ture space are not required at all.

To explain what a kernel trick is and how it works,

B. Scho

lkopf [8] gave an example, as shown in Fig. 1.

In the example, the two-class data is linearly non-

separable in the two-dimensional input space. That is,

one cannot ﬁnd a projection axis by using any linear

dimension reduction technique such that the projected

data is separable on this axis. To deal with this problem,

the data can be transformed into a feature space by

the map F given in Fig. 1. As a result, the data become

linear separable in the yielding three-dimensional

feature space, thereby the linear dimension reduction

technique can be applied in such a space. To imple-

ment a linear dimension reduction technique in the

feature space, one needs to calculate the inner product

as follows:

hFðxÞ; Fðx

Þi ¼ ðx

;

ﬃﬃﬃ

; x

Þðx

;

ﬃﬃﬃ

; x

¼hx; x

¼ :kðx; x

Therefore, the inner product operation can be expres-

sed by a 2-order polynomial kernel function. In this

way, the operation of the inner product in the feature

space is essentially avoided, as it can be calculated in

the input space via a kernel function. In addition, one

need not construct an explicit map, since the map is

completely determined by the kernel function.

Now, KPCA and KFD can be outlined as follows.

Given a set of M training samples x

; x

; ; x

, the covariance operator on the feature space H

can

be constructed by

j¼1

Fðx

Þm



Fðx

Þm



ð2Þ

where m

j¼1

Fðx

Þ, and F is a map into the

feature space H

which is determined by a kernel k.In

a ﬁnite-dimensional Hilbert space, this operator is

generally called the covariance matrix.

Non-linear Techniques for Dimension Reduction. Figure 1 An example of kernel mapping. (a) The data is linearly non-

separable in the input space. (b) The data is linearly separable in the mapped feature space.

1004

Non-linear Techniques for Dimension Reduction

It is easy to show that every eigenvector of S

, b,

can be linearly expanded by

b ¼

i¼1

Fðx

Þ: ð3Þ

To obtain the expansion coefﬁcients, one can con-

struct the M  M Gram matr ix K with elements

¼ kðx

; x

Þ and centralize K as follows

K ¼ðI  DÞKðI  DÞ; where I is the

identity matrix and D ¼ð1

MÞ

MM

ð4Þ

Calculate the orthonormal eigenvectors v

; v

; ; v

K corresponding to the m largest positive eigenva-

lues l

; l

; ; l

. The orthonormal eigenvectors

; b

; ; b

of S

corresponding to the m largest

positive eigenvalues l

; l

; ; l

are

ﬃﬃﬃﬃ

j ¼ 1; ; m

where

Q ¼ Fðx

Þ; ; Fðx

Þ½

ð5Þ

After the projection of the centered, mapped sample

FðxÞ on to the eigenvector system b

; b

; ; b

one can obtain the KPCA-transformed feature vector

y by

y ¼ðb

; b

; ; b

½FðxÞm



¼ L



½FðxÞm



¼ L



ðI  DÞðK

 KD

ð6Þ

where

L ¼ diagðl

; l

; ; l

Þ; V ¼½v

; v

; ; v

;

and

¼ kðx

; xÞ; kðx

; xÞ; ; kðx

; xÞ½

and

¼ð1=MÞ

M1

KFD seeks a set of optimal discriminant vectors by

maximizing the Fisher criterion in the feature space.

KFD can be derived in the similar way as used in KPCA.

That is, the Fisher discriminant vector can be expanded

using Eq. (3) and then the problem is formulated in a

space spanned by all mapped training samples. (For

more details, please refer to [2, 3].) Recent works

[9, 10] revealed that KFD is equivalent to KPCA plus

LDA. Based on this result, a more transparent KFD

algorithm has been proposed. That is, KPCA is ﬁrst

performed and then LDA is used for a second dimen-

sion reduction in the KPCA-transformed space.

Manifold Learning Related Non-Linear

Dimension Reduction Techniques

Of late, manifold learning has become very popular in

machine learning and pattern recognition areas. As-

sume that the data lie on a low-dimensional manifold.

The goal of manifold learning is to ﬁnd a low-dimen-

sional representation of data, and to recover the struc-

ture of data in an intrinsically low-dimensional space.

To gain more insight into the concept of manifold

learning, one can begin with a fundamental problem:

how is the observation data on a manifold generated?

Suppose the data is generated by the following model:

f ðYÞ!X; ð7Þ

where Y is the parameter set, and f can be viewed as a

non-linear map. Then, its inverse problem is: how can

one recover the parameter set without knowing the

map f ? How can one build a map f from the data

space to the parameter space? Manifold learning

seeks answers to these problems. The process of

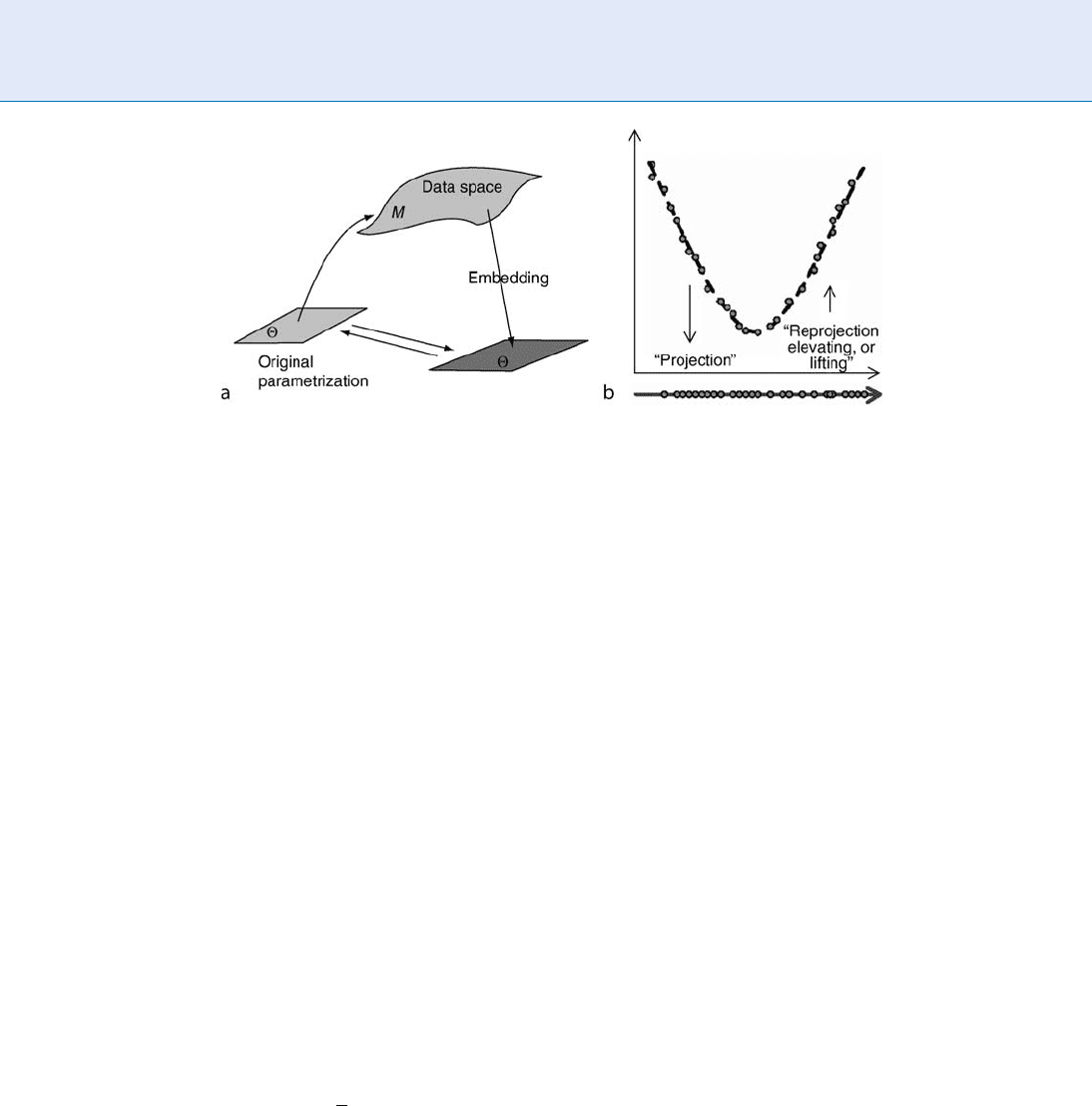
manifold learning is illustrated in Fig . 2 ; Fig . 2 (a)

presents a general process of manifold learning [11],

and Fig . 2( b) shows an example of how to ﬁnd a

one-dimensional embedding (parameter set) from

the two-dimensional data lying on a one-dimensional

manifold [12].

Many manifold learning related dimension reduc-

tion techniques have been developed over the last few

years. Among the most well-known are isometric fea-

ture mapping (ISOMAP) [4], local linear embedding

(LLE) [5], and Laplacian Eigenmap [6]. Here, LLE can

be considered as an example to introduce manifold

learning related dimension reduction techniques.

Let X ¼fx

; x

; ; x

g be a set of N points in a

high-dimensional observation space

. The data points are assumed to lie on or close

to a low-dimensional manifold. LLE seeks to ﬁnd a

low-dimensional embedding of X by mapping the data

into a single global coordinate system in R

(d < n).

The corresponding set of N points in the embedding

space R

can be denoted as Y ¼fy

; y

; ; y

The LLE algorithm is outlined in the following

three steps.

Non-linear Techniques for Dimension Reduction

1005

Step 1: For each data point x

2 X, ﬁnd K nearest

neighbors of x

. Let O

¼fjjx

belongs to the set

of K nearest neighbors of x

Step 2: Reconstruct x

from its K nearest neighbors

identiﬁed. The reconstruction weights can be

obtained by minimizing the reconstruction error

¼ x





; ð8Þ

subject to

¼ 1 and w

¼ 0 for any j =2 O

Suppose the optimal reconstruction weights are



ði; j ¼ 1; 2; ; NÞ.

Step 3: Compute d-dimensional coordinates y

minimizing the embedding cost function

FðyÞ¼







: ð9Þ

subject to the following two constraints

¼ 0 and

¼ I; ð10Þ

where I is an identity matrix.

The process of LEE algorithm is illustrated in Fig. 1 of

SVM and Kernal Method by Scho

lkopf [8].

Although some previous experiments have demon-

strated that the LEE and ISOMAP methods can pro-

vide perceptually meaningful representation for facial

expression or pose variations, these manifold learning

methods may not be suitable for biometric recogni-

tion tasks. [13] First, the goal of these manifold

learning algorithms has no direct connections to clas-

siﬁcation. Second, these algorithms are inconvenient

to deal with new samples because the involved non-

linear map is unknown. How to model biometric

manifolds and develop effective manifold learning

algorithms for classiﬁcation purp oses deserve further

investigation.

Summary

Two kinds of non-linear dimension reduction techni-

ques, kernel-based methods and manifold learning

related algorithms, have been introduced here. The

mechanism of kernel methods is to increase the dimen-

sion ﬁrst by an implicit non-linear map determined by

a kernel and then to reduce the dimension in the

feature space, while that of manifold learning related

algorithms is to reduce the dimension directly via a

non-linear map. Recent research on these two kinds of

dimension reduction techniques has revealed an inter-

esting result: manifold learning al gorithms, such as

ISOMAP, local linear LLE, and Laplacian Eigenmap,

can be described from a kernel po int of view [14].

Related Entries

▶ Biometrics, Overview

▶ Kernel Methods

▶ Linear Techniques for Dimension Reduction

▶ Manifold Learning

▶ Non-Linear Dimension Reduction Methods

Non-linear Techniques for Dimension Reduction. Figure 2 Illustration of the process of manifold learning. (a) A general

process of manifold learning [11]. (b) An example of how to derive a one-dimensional embedding from the

two-dimensional data lying on a one-dimensional manifold [12].

1006

Non-linear Techniques for Dimension Reduction

References

1. Scho

lkopf, B., Smola, A., Muller, K.R.: Nonlinear component

analysis as a kernel eigenvalue problem. Neural Comput. 10(5),

1299–1319 (1998)

2. Mika, S., Ra

tsch, G., Weston, J., Scho

lkopf, B., Mu

ller, K.R.:

Fisher discriminant analysis with kernels. IEEE International

Workshop on Neural Networks for Signal Processing IX, Madi-

son (USA), August 1999, pp. 41–48

3. Baudat, G., Anouar, F.: Generalized discriminant analysis using a

kernel approach. Neural Comput. 12(10), 2385–2404 (2000)

4. Tenenbaum, J.B., de Silva, V., Langford, J.C.: A global geometric

framework for nonlinear dimensionality reduction. Science 290,

2319–2323 (2000)

5. Roweis, S.T., Saul, L.K.: Nonlinear dimensionality reduction

by locally linear embedding. Science. 290, 2323–2326 (2000)

6. Belkin, M., Niyogi, P.: Laplacian eigenmaps for dimensionality

reduction and data representation. Neural Comput. 15(6),

1373–1396 (2003)

7. Yan, S., Xu, D., Zhang, B., Zhang, H.J., Yang, Q., Lin, S.: Graph

embedding and extensions: A general framework for dimension-

ality reduction. IEEE Trans. Pattern Anal. Mach. Intell. 29(1),

40–51 (2007)

8. Scho

lkopf, B.: SVM and Kernel Method. http://www.kernel-

machines.org/

9. Yang, J., Jin, Z., Yang, J.Y., Zhang, D., Frangi, A.F.: Essence

of Kernel Fisher Discriminant: KPCA plus LDA, Pattern Recogn.

37(10), 2097–2100 (2004)

10. Yang, J., Frangi, A.F., Yang, J.Y., Zhang, D., Zhong, J.: KPCA plus

LDA: A complete kernel ﬁsher discriminant framework for fea-

ture extraction and recognition. IEEE Trans. Pattern. Anal.

Mach. Intell. 27(2), 230–244 (2005)

11. Grimes, C., Donoho, D.: Can these things really work? Theoretical

Results for ISOMAP and LLE, a presentation at the Workshop of

Spectral Methods in Dimensionality Reduction, Clustering, and

Classiﬁcation in NIPS 2002. http://www.cse.msu.edu/lawhiu/

manifold/

12. McMillan, L.: Dimensionality reduction Part 2: Nonlinear meth-

ods. http://www.cs.unc.edu/Courses/comp290-90-f03/

13. Yang, J., Zhang, D., Yang, J.Y., Niu, B.: Globally maximizing,

locally minimizing: Unsupervised discriminant projection with

applications to face and palm biometrics. IEEE Trans Pattern

Anal. Mach. Intell. 29(4), 650–664 (2007)

14. Ham, J., Lee, D., Mika, S., Scho

lkopf, B.: A kernel view of the

dimensionality reduction of manifolds. In: Proceedings of the

Twenty-First International Conference on Machine Learning,

Alberta, Canada, pp. 369–376 (2004)

Normalised Hamming Distance

▶ Score Normalization Rules in Iris Recognition

Nuisance Attribute Projection

▶ Session Effects on Speaker Modeling

Numerical Standard

Minimal number of corresponding minutiae between a

ﬁngermark and a ﬁngerprint necessary for a formal

identiﬁcation, in absence of signiﬁcant difference.

▶ Fingerprint, Forensic Evidence of

Numerical Standard

1007

Object Recognition

Given a few training image of the same target object

(same object, bu t may be viewed from different ang les

or position), the goal of object recognition is to retrieve

the same object in other unseen images. It is a difﬁcult

problem because the target object in unseen image may

appear different from what it appears in the training

image, due to the variation of view points, background

clutter, ambient illumi nation, partially occluded by

other object or deformation of the object itself. A

good object recognition algorithm is supposed to be

able to recognize target object given all of the above

variations.

▶ Iris Super-Resolution

Observations from Speech

▶ Speaker Features

Ocular Biometrics

▶ Retina Recognition

Odor Biometrics

ADEE A. SCHOON

,ALLISON M. CURRAN

ENNETH G. FURTON

Animal Behavior Group, Leiden University, Leiden,

The Netherlands

Department of Chemistry and Biochemistry,

International Forensic Research Institute, Florida

International University, Miami, FL, USA

Synonyms

Osmology; Scent identiﬁcation line-ups

Definition

Human odor can be differentiated among individuals

and can therefore be see n as a biometric that can be

used to identify this person. Dogs have been trained to

identify objects held by a speciﬁc person for forensic

purposes from the beginning of the twentieth centur y.

Advancing technology has made it possible to identify

humans based on

▶ headspace analysis of objects they

have handled, opening the route to the use of odor as a

biometric.

Introduction

From the early twentieth century, dogs have been used

to ﬁnd and identify humans based on their odor. This

has originated from the capacity of dogs to follow the

track of a person, either by following the odor the

person left directly on the ground that the dog needed

to follow quite closely (‘‘tracking’’), or by following

a broader odor trail that the dogs could follow at

some distance (‘‘trailing’’). Some dogs were very

2009 Springer Science+Business Media, LLC