Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

▶ Multi-Samp le Systems

▶ Multi-Sensor System s

▶ Multi-Unit Systems

▶ Multiple Classiﬁer Sys tems

▶ Multiple Experts

▶ Score-Level Fusion

References

1. Korves, H., Nadel, L., Ulery, B., Masi, D.: Multibiometric fusion:

From research to operations. Mitretek Sigma, Summer 2005

(2005)

2. ISO/IEC JTC 1/SC 37 Standing Document 2 – Harmonized

Biometric Vocabulary, ISO/IEC JTC 1/SC 37 N2263 (2007)

3. Jain, A.K., Nandakumar, K., Ross, A.: Score normalization in

multimodal biometric systems. Pattern Recognit. 38(12),

2270–2285 (2005)

4. Wang, Y., Tan, T., Jain, A.K.: Combining face and iris biometrics

for identity veriﬁcation. In: Proceedings of the Fourth Interna-

tional Conference on Audio- and Video-Based Biometric Person

Authentication, Guildford, UK, pp. 805–813 (2003)

5. Kittler, J., Hatef, M., Duin, R.P., Matas, J.G.: On combining

classiﬁers. IEEE Trans Pattern Anal. Mach. Intell. 20(3),

226–239 (1998)

6. Neyman, J., Pearson, E.S.: On the problem of the most efﬁcient

tests of statistical hypotheses. Philos. Trans. R. Soc. Lond A. 231,

289–337 (1933)

7. Ross, A., Govindarajan, R.: Feature level fusion using hand and

face biometrics. In: Proceedings of the SPIE Conference on

Biometric Technology for Human Identiﬁcation, Orlando,

USA, pp. 196–204 (2005)

8. Chang, K., Bowyer, K.W., Sarkar, S., Victor, B.: Comparison and

combination of ear and face images in appearance-based

biometrics. IEEE Trans. Pattern Anal. Mach. Intell. 25(9),

1160–1165 (2003)

9. Kumar, A., Wong, D.C.M., Shen, H.C., Jain, A.K.: Personal

veriﬁcation using palmprint and hand geometry biometric. In:

Proceedings of the Fourth International Conference on Audio-

and Video-Based Biometric Person Authentication, Guildford,

UK, pp. 668–678 (2003)

10. ISO/IEC TR 24722:2007, Information technology – Biometrics –

Multimodal and other multibiometric fusion (2007)

11. ANSI INCITS 439, Information Technology – Fusion Informa-

tion Format for Data Interchange (2008)

12. ISO/IEC 19784-1:2006, Information technology – Biometric

Application Programming Interface – Part 1: BioAPI Speciﬁca-

tion (2006)

13. ANSI INCITS 358–2002, Information technology – BioAPI

Speciﬁcation (2002)

14. ANSI INCITS 358-2002/AM1-2007, Information technology –

BioAPI Speciﬁcation – Amendment 1: Support for Biometric

Fusion (2007)

15. ISO/IEC 24713–3, Information technology – Biometric proﬁles

for interoperability and data interchange – Part 3: Biometric

based veriﬁcation and identiﬁcation of Seafarers (2008)

Multifactor

Multifactor authentication/identiﬁcation solutions

consist of a combination (integrated or loosely linked)

of different categories of authentication and identiﬁca-

tion technologies. A multifactor solution could thus be

composed of a ﬁngerprint recognition system tied to a

proximity card reader and a PIN-based keypad system.

▶ Fraud Reduction, Overview

Multimodal

▶ Multibiometrics

Multimodal Fusion

▶ Multiple Experts

Multimodal Jump Kits

A compact, durable, and mobile kit that encases mul-

tiple biometric testing devices. An example kit is a

briefcase that contains digital ﬁngerprints, voice and

iris prints, and photographs.

▶ Iris Acquisition Device

Multiple Classifier Fusion

▶ Fusion, Decision-Level

980

Multifactor

Multiple Classifier Systems

FAB IO ROLI

Department of Electrical and Electronic Engineering ,

University of Cagliari, Piazza d’Armi, Cagliari, Italy

Synonyms

Classiﬁer combination; Ensemble learning; Multiple

classiﬁers; Multiple expert systems

Definition

The rationale behind the growing interest in multiple

classiﬁer systems is the acknowledgment that the clas-

sical approach to design a pattern recognition system

that focuses on ﬁnding the best individual classiﬁer has

some serious drawbacks. The most common type of

multiple classiﬁer system (MCS) includes an ensemble

of classiﬁers and a function for parallel combination of

classiﬁer outputs. However, a great number of methods

for creating and combining multiple classiﬁers have

been proposed in the last 15 years. Alth ough reported

results showed the good performances achievable by

combining multiple classiﬁers, so far a designer of

pattern classiﬁcation systems should regard the MCS

approach as an additional tool to be used when build-

ing a single classiﬁer with the required performance is

very difﬁcult, or does not allow exploiting the comple-

mentary discriminatory informati on that other classi-

ﬁers may encapsulate.

Motivations of Multiple Classifiers

The traditional approach to classiﬁer design is based

on the ‘‘evaluation and selection’’ method. Perfor-

mances of a set of different classiﬁcation algorithms

are assessed against a data set, name validation set, and

the best classiﬁer is selected. This approach works well

when a large and representative data set is available, so

that the estimated performances allow selecting the

best classiﬁer for future data collected during the oper-

ation of the classiﬁer machine. However, in many real

cases where only small training sets are available, esti-

mated performances can substantially differ from the

ones that classiﬁers will exhibit during their operation.

This is the well-known phenomenon of the generaliza-

tion error, which can makes impossible the selection of

the best individual classiﬁer, or cause the selection of a

classiﬁer with a poor performance. In the worst case,

the worst classiﬁer in the considered ensemble could

exhibit the best apparent accuracy when assessed

against a small vali dation set.

A ﬁrst motivation for the use of multiple classiﬁers

comes from the intuition that instead of selecting a

single classiﬁer, a safer option would be to use them all

and ‘‘average’’ their outputs [1, 2]. This combined

classiﬁer might not be better than the individual best

classiﬁer, but the combination should reduce the risk

of selecting a classiﬁer with poor performance. Experi-

mental evidences and theoretical results support this

motivation. It has been proved that averaging the out-

puts of multiple classiﬁers do eliminates the risk of

selecting the worst classiﬁer, and can provide a perfor-

mance better than the one of the best classiﬁer under

particular conditions [3].

Dietterich suggested further reasons for the use of

a multiple classiﬁer system (MCS) [2]. Some classiﬁers,

such as neural networks, are trained with algorithms

that may lead to different solutions, that is, different

classiﬁcation accuracies, depending on the initial

learning conditions. Combining multiple classiﬁers

obtained with different initi al learning conditions

(e.g., different initial weights for a neural net), reduces

the risk of selecting a classiﬁer associated to a poor

solution of the learning algorithm (a so called ‘‘local

optimum’’). The use of MCS can simplify the problem

of choosing adequate values for some relevant para-

meters of the classiﬁcation algorithm (e.g., the number

of hidden neurons in a neural net). Multiple versions

of the same classiﬁer with different values of the para-

meters can be combined. In some practical cases with

small training sets, training and combining an ens-

emble of simple classiﬁe rs (e.g., linear classiﬁers) to

achieve a certain high accuracy can be easier than

training directly a complex classiﬁer [4]. Finally, for

some applications, such as multi-modal biometrics,

the use of multiple classiﬁers is naturally motivated

by application requirements.

It is worth noting that the above motivations neither

guarantee that the combination of multiple classiﬁers

always performs better than the best individual classiﬁer

in the ensemble, nor an improvement on the ensemble’s

average performance for the general case. Such guaran-

tees can be given only under particular conditions that

Multiple Classifier Systems

981

classiﬁers and the combination function have to satisfy

[3]. However, reported experime ntal results and theo-

retical works developed for par ticular combination

functions show the good performances achiev able

by combining multiple classiﬁers. So far a designer of

pattern classiﬁcation systems should regard the MCS

approach as an additional tool to be used when build-

ing a single classiﬁer with the required performance is

very difﬁcult, or does not allow exploiting the comple-

mentary discriminatory informati on that other classi-

ﬁers may encapsulate.

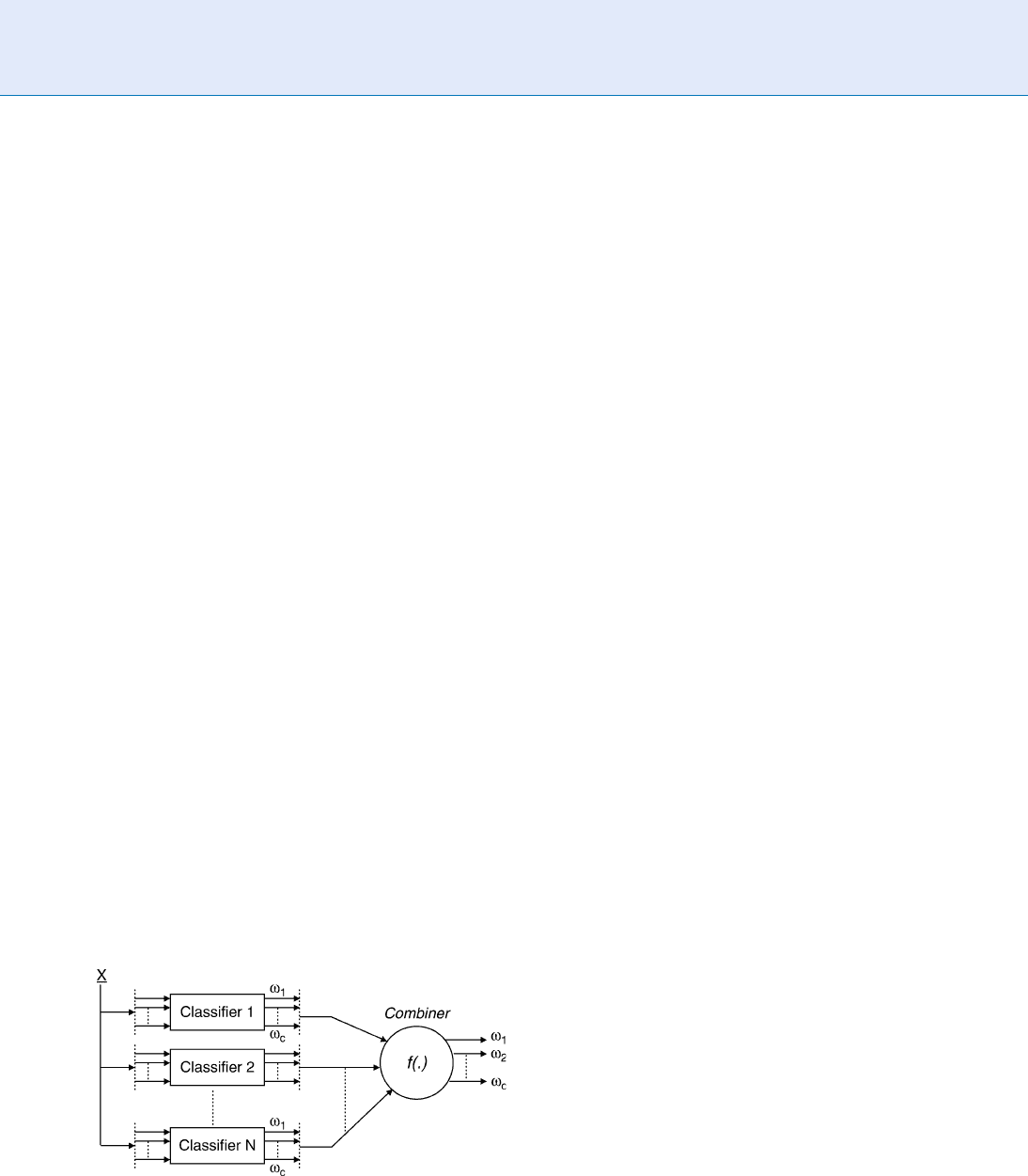
Design of Multiple Classifier Systems

The most common type of MCS, widely used and

investigated, includes an ensemble of classiﬁers,

named

▶ ‘‘base’’ classiﬁers, and a function for parallel

combination of classiﬁer outputs (Fig. 1). The base

classiﬁers are often algorithms of the same type (e.g.,

decision trees or neural networks), and statistical clas-

siﬁers are the most common choice. The use of hybrid

ensembles containing different types of algorithms

has been investigated much less, as well as ensembles

of structural classiﬁers have not attracted much atten-

tion, though they could be important for some real

applications.

The design of a MCS involves two main phases: the

design of the classiﬁer ensemble and the design of the

combination function [4]. Although this formulation

of the design problem leads one to think that effective

design should address both the phases, most of the

design methods described in the literature focused

on only one. Two main design approaches have been

proposed, that Ho called ‘‘coverage optimization’’ and

‘‘decision optimization’’ methods [5]. Coverage opti-

mization refers to methods that assume a ﬁxed, usually

simple, decision combination function and aim to

generate a set of mutually complementary classiﬁers

that can be combined to achieve optimal accuracy.

Several techniques have been proposed for creating a

set of mutually complementary classiﬁers. The main

approaches are outlined in the following. However,

decision optimization methods assume a given set

of carefully designed classiﬁers and aim to select and

optimize the combination function. These metho ds ﬁt

well with those applications where a set of classiﬁers

developed separately is already available (e.g., a face

and a ﬁngerprint classiﬁer in biometric applications)

and one is interested in combining them optimally.

A large set of combination functions of increasing

complexity is available to the designer to perform the

selection and optimization, ranging from simple vot-

ing rules through ‘‘trainable’’ combination functions.

The three main types of combination functions are

brieﬂy explained below. There are few methods for

building a MCS that cannot be classiﬁed as either a

decision optimization or a coverage optimization

method. For example, MCS based on the mixture of

experts model trains the classiﬁers and the combi-

nation function simultaneou sly, so implementing a

sort of joint optimization [6]. In some works dealing

with real-life applications, hybrid design methods that

ﬁrst generate a classiﬁer ensemble and then select and

optimize the combination function have been also

proposed.

It is easy to see that the classiﬁers in a MCS should

be as accurate as possible and should not make coinci-

dent errors. Although this sounds an intuitive and

simple concept, it revealed a complex issue that was

addressed in the literature under the name of classiﬁer

‘‘diversity’’ [1, 7]. The type of diversity required for

maximizing MCS performance obviously depends on

the combination function used. As an example, coin-

cident errors can be tolerated if the majority-voting

rule is used, but the majority of classiﬁer decisions

should be always correct. Many diversity measures

have been proposed, and some of them have been

also used to design effective MCSs [4]. The main

approaches for creating multiple classiﬁers, which are

outlined in the following, aim to induce classiﬁer di-

versity. However, so far it appeared to be difﬁcult to

Multiple Classiﬁer Systems. Figure 1 Standard

architecture of a multiple classifier system for a

classification task with c classes. The multiple classiﬁer

system is made up by an ensemble of N classiﬁers and a

function for parallel combination of classiﬁer outputs.

982

Multiple Classifier Systems

deﬁne diversity measures that are related well to the

MCS performance, so that such performance can be

predicted by measuring the diversity of the classiﬁers.

Although the parallel architecture was the most

used and investigated (Fig. 1), other types of architec-

tures are also possible. For example, serial architectures

where classiﬁers are applied in succession, with each

classiﬁer working on inputs, which previous classiﬁers

were not able to recognize w ith a sufﬁcient conﬁdence.

Such architectures could be very important for real

applications that demand for a trade-off between ac-

curacy and computational complexity. However, non-

parallel architectures have been relatively neglected.

Although some design methods proved to be very

effective and some works investigated the comparative

advantages of different methods [4, 5], clear guidelines

are not yet available for choosing the best design meth-

od for the classiﬁcation task at hand. The designer of

MCS has a toolbox containing quite a lot of instru-

ments for generating and combining classiﬁers. She/he

may design a myriad of different MCSs by coupling

different techniques for creating classiﬁer ensembles

with different combination functions. However, for

the general case, the best MCS can only be determined

by performance evaluation. Optimal design is possible

only under particular assumptions on the classiﬁers

and the combination func tion [3].

Creating Classifier Ensembles

Several techniques hav e been proposed for creating a set

of complementary classiﬁers. All these techniques try to

induce classiﬁer diversity, namely , to create classiﬁers

that make errors on differ ent patterns, so that they can

be combined effectively. In the following, the main

approaches to classiﬁer ensemble generation are outlined.

Using Different Base Classifiers

A simple way for generating multiple classiﬁers is using

base classiﬁers of different types. For example, classi-

ﬁers based on different models (e.g., neural networks

and decisio n trees) or using different input informa-

tion. This simple technique may work well for applica-

tions where complementary information sources are

available (e.g., multi-sensor applications) or distinct

representations of patterns are possible (e.g., minu-

tiae-based and texture-based representations in ﬁnger-

print classiﬁcation).

Injecting Randomness

Random variation of some parameters of the learning

or classiﬁcation algorithm can be used to create multi-

ple classiﬁers. The classiﬁer ensemble is created using

multiple versions of a certain base classiﬁer obtained

by random variation of some parameters. For example,

training a neural network several times with different

random values of the initial weights allows generating a

network ensemble.

Manipulating Training Data

These techniques generate multiple classiﬁers by train-

ing a base classiﬁer with different data sets. To this end,

the most straightforward method is the use of disjoint

training sets obtained by splitting the original training

set (this technique is called sampling without replace-

ment). A very popular technique based on training

data manipulation is Bagging (Bootstrap AGGregat-

ING) [8]. Bagging creates an ensemble made of N

classiﬁers trained on N bootstrap replicates of the

original training set. A bootstrap replicate consists of

a set of m patterns drawn randomly with replacement

from the original training set of m patterns. The clas-

siﬁers are usually combined by majority voting rule, or

by averaging their outputs. Another po pular techn ique

based on training data manipulation is Boosting [9].

This method incrementally builds a classiﬁer ensemble.

The classiﬁer that joins the ensemble at step k is forced

to learn patterns that previous classiﬁers have misclas-

siﬁed. In other words, while Bagging samples each

training pattern with equal probability, Boosting fo-

cuses on those training patterns that are most often

misclassiﬁed. Essentially, a set of weights is maintained

over the training set and adaptive resampling is per-

formed, such that the weights are increased for those

patterns that are misclassiﬁed. It is worth noting that

Boosting is a complete design method, where the com-

bination function is also speciﬁed, and it is not only a

technique for generating a classiﬁer ensemble.

Manipulating Input Features

Manual or aut omatic feature selection can be used for

generating multiple classiﬁers using different feature

sets as inputs. Ho proposed a successful technique of

this type, call ed Random Subspace Method [10]. Fea-

ture space is randomly sampled, such that complemen-

tar y classiﬁers are obtained by training them with

different feature sets.

Multiple Classifier Systems

983

Manipulating Output Labels

A multiclass problem can be subdivided into a set of

subproblems (e.g., two-class problems), and a classiﬁer

can be associated to each subproblem, thereby gener-

ating an ensemble. The standard problem subdivision

is the so-called ‘‘one-per-class’’ decomposition, where

each classiﬁer in the ensemble is associated to one of

the classes and it is aimed to discriminate such class

from the others. Dietterich and Bakiri proposed a

general method, called ECOC (error correcting output

codes) method, for generating multiple classiﬁers by

decomposing a multiclass task into subtasks [11].

Combining Multiple Classifiers

There are two main strategies in combining classiﬁers:

fusion and selection [1]. The most of the combination

functions follow one of these basic strategies, with the

majority of combination methods using the fusion strat-

egy. There are few combiners that use hybrid strategies,

where fusion and selection are merged. In classiﬁer fu-

sion, each classiﬁer contributes to the ﬁnal decision for

each input pattern. In classiﬁer selection, each classiﬁer

is supposed to have a speciﬁc domain of competence

(e.g., a region in the feature space) and is responsible for

the classiﬁcation of patterns in this domain. There are

combination functions lying between these two main

strategies. For example, the mixture of experts model

uses a combination strategy that, for each input pattern,

selects and fuses a subset of available classiﬁers [6]. Some

combination functions, such as the majority-voting

rule, are called ‘‘ﬁxed’’ combiners because they do not

need training (i.e., they do not nee d estimation of

parameters from a training set). Other combination

functions need additional training and they are called

‘‘trainable’’ combiners. For example, the weighted

majority-voting rule needs to estimate weights that

are used to give different importance to the classiﬁers

in the vote. Trainable combiners can obviously outper-

form the ﬁxed ones, supposed that a large enough and

independent validation set for training them in an

effective way is available [4]. It should be noted that

each classiﬁer in the ensemble is often biased on the

training data, so that the combiner should not be

trained on such data. An additional data set that is

independent from the training set used for the individ-

ual classiﬁers should be used. In general, the complex-

ity of the combiner should be adapted to the size of the

data set available. Complex trainable combiners, that

need to estimate a lot of parameters, should be used

only when large data sets are available [1, 12].

Fusion of Multiple Classifiers

The combination functions following the fusion strat-

egy can be classiﬁed on the basis of the type of outputs

of classiﬁers forming the ensemble. Xu et al. distin-

guish between three types of classiﬁer outputs [13]: (1)

Abstract-level output: Each classiﬁer outputs a unique

class label for each input pattern; (2) Rank-level out-

put: Each classiﬁer outputs a list of ranked class labels

for each input pattern. The class labels are ranked in

order of plausibility of being the correct class label;

(3) Measurement-level output: Each classiﬁer outputs

a vector of continuous-valued measures that represent

estimates of class posterior probabilities or class-

related conﬁdence values that represent the support

for the possible classiﬁc ation hypotheses. On the

basis of this classiﬁcation, the following three classes

of fusion rules can be deﬁned.

Abstract-Level Fusion Rules

Among the fusion rules that use only class labels

to combine classiﬁer outputs, the most often used

rule is the majority vote that assigns the input pattern

to the majority class, that is, the pattern is assigned

to the most frequent class in the classiﬁer outputs.

A natural variant of the majority vote, namely, the

plurality vote, is also used. The trainable version of

the majority vote rule is the weighted majority vote

that uses weights that are usually related to the classiﬁ-

er performances. Among the trainable fusion rules of

this type, a popular rule is the Behavior Knowledge

Space (BKS) method [1]. In the BKS method, every

possible combination of abstract-level classiﬁers outputs

is regarded as a cell in a look-up table. The BKS table is

of the training set characterized by a particular value of

class labels. Training samples in each cell are subdivided

per class, and the most representative class label (the

‘‘majority’’ class) is selected for each cell. For each un-

known test pattern, the classiﬁcation is performed

according to the class label of the BKS cell indexed by

the classiﬁer outputs. The BKS method requires very

large and representative data sets to work well.

Rank-Level Fusion Rules

The most commonly used rule of this type is the Borda

Count method. The Borda count method combines

984

Multiple Classifier Systems

the lists of ranked class labels provided by classiﬁers ,

and it classiﬁes an input pattern by its overall class

rank, that is computed summing the rank values

that classiﬁers assigned to the pattern for each class.

The class with the maximum overall rank is the winner.

Rank-level fusion rules are suitable for problems

with many classes, where the correct class may appear

often near the top of the list, although not always at

the top.

Measurement-Level Fusion Rules

Examples of ﬁxed rules that combine continuous clas-

siﬁer outputs are: the simple mean (average), the max-

imum, the minimum, the median, and the product of

classiﬁer outputs [1]. Linear combiners (i.e., the aver-

age and its trainable version, the weighted average) are

used in popular ensemble learning algorithms such as

Bagging [8], the Random Subspace Method [10], and

AdaBoost [1, 9], and represent the baseline and ﬁrst

choice combiner in many applications. Continuous

classiﬁer outputs can be also regarded as a new feature

space (an intermediate feature space [1]). Another

classiﬁer that takes classiﬁer outputs as input and out-

puts a class label can do the combination. However,

this approach usually demands very large data sets that

allow training effectively this additional classiﬁer. The

Decision Templates method is an interesting example

of a trainable rule for combining continuous classiﬁer

outputs [1]. The idea behind decision templates com-

biner is to store the most typical classiﬁer outputs

(called decision template) for each class, and then

compare it with the classiﬁer outputs obtained for

the input pattern (called decision proﬁle of the input

pattern) using some similarity measure.

Selection of Multiple Classifiers

In classiﬁer selection, the role of the combiner is selecting

the classiﬁer (or the subset of classiﬁers) to be used for

classifying the input pattern, under the assumption that

different classiﬁers (or subsets of classiﬁers) hav e different

domains of competence. Dynamic classiﬁer selection

rules have been proposed that estimate the accuracy of

each classiﬁer in a local region surrounding the pattern to

be classiﬁed, and select the classiﬁer that exhibits the

maximum accuracy [14, 15]. As dynamic selection

may be too computationally demanding and require

large data sets for estimating the local classiﬁer accura-

cy, some static selection rules have also been proposed

where the regions of competence of each classiﬁer are

estimated before the operational phase of the MCS [1].

Classiﬁer selection has not attracted as much atten-

tion as classiﬁer fusion, probably due to the practical

difﬁculty of identifying the domains of competence

of classiﬁers that make possible an effective selection.

Related Entries

▶ Ensemble Learning

▶ Fusion, Decision-Level

▶ Fusion, Rank-Level

▶ Fusion, Score-Level

▶ Multi-Algorithm Systems

▶ Multiple Experts

References

1. Kuncheva, L.I.: Combining Pattern Classiﬁers: Methods and

Algorithms, Wiley, NY (2004)

2. Dietterich, T.G.: Ensemble methods in machine learning, Multi-

ple Classiﬁer Systems, Springer-Verlag, LNCS, 1857, 1–15 (2000)

3. Fumera, G., Roli, F.: A Theoretical and experimental analysis of

linear combiners for multiple classiﬁer systems. IEEE Trans.

Pattern Anal. Mach. Intell. 27(6), 942–956 (2005)

4. Roli F., Giacinto, G.: Design of multiple classiﬁer systems. In:

Bunke, H., Kandel, A. (eds.) Hybrid Methods in Pattern Recog-

nition, World Scientiﬁc Publishing (2002)

5. Ho, T.K.: Complexity of classiﬁcation problems and compara-

tive advantages of combined classiﬁers, Springer-Verlag, LNCS,

1857, 97–106 (2000)

6. Jacobs, R., Jordan, M., Nowlan, S., Hinton, G.: Adaptive mix-

tures of local experts. Neural Comput. 3, 79–87 (1991)

7. Kuncheva, L.I., Whitaker, C.J.: Measures of diversity in classiﬁer

ensembles. Mach. Learn. 51, 181–207 (2003)

8. Breiman, L.: Bagging predictors. Mach. Learn. 24, 123–140

(1996)

9. Freund, Y., Schapire, R.E.: A decision-theoretic generalization of

on-line learning and an application to boosting. J. Comput. Syst.

Sci. 55(1), 119–139 (1997)

10. Ho, T.K.: The random subspace method for constructing deci-

sion forests. IEEE Trans. Pattern Anal. Mach. Intell. 20, 832–844

(1998)

11. Dietterich, T.G., Bakiri, G.: Solving multiclass learning problems

via error-correcting output codes. J. Artif. Intell. Res. 2, 263–286

(1995)

12. Roli, F., Raudys, S., Marcialis, G.L.: An experimental comparison

of ﬁxed and trained fusion rules for crisp classiﬁers outputs. In:

Proceedings of the third International Workshop on Multiple

Classiﬁer Systems (MCS 2002), Cagliari, Italy, June 2002, LNCS

2364, 232–241 (2002)

Multiple Classifier Systems

985

13. Xu, L., Krzyzak, A., Suen, C.Y.: Methods for combining multiple

classiﬁers and their applications to handwriting recognition.

IEEE Trans. Syst. Man Cybern. 22(3), 418–435 May/June (1992)

14. Woods, K., Kegelmeyer, W.P., Bowyer, K.: Combination of mul-

tiple classiﬁers using local accuracy estimates. IEEE Trans. Pat-

tern Anal. Mach. Intell. 19(4), 405–410 (1997)

15. Giacinto, G., Roli, F.: Dynamic Classiﬁer Selection Based on

Multiple Classiﬁer Behavior. Pattern Recognit. 34(9), 179–181

(2001)

Multiple Classifiers

▶ Multiple Classiﬁer Systems

Multiple Expert Systems

▶ Multiple Classiﬁer Systems

Multiple Experts

JOSEF BIGU N

Halmstad University, IDE, Halmstad, Sweden

Synonyms

Decision fusion; Feature fusion; Fusion; Multimodal

fusion; Score fusion

Definition

A Biometric expert, or an expert in bio metric recogni-

tion context, refers to a method that expresses an

opinion on the likelihood of an identity by analyzing

a signal that it is specialized on, e.g. a ﬁngerprint expert

using minutiae, a lip-motion expert using statistics of

optical-ﬂow. Accordingly, there can be several experts

associated with the same sensor data, each analyzing

the data in a different way. Alternatively, they can be

specialized on different sensor data. Multiple experts

can address the issue of how expert opinions should

be represented and reconciled to a single opinion on

the authenticity of a

▶ client identity.

Introduction

In biometric signal analysis, the fusion of multiple

experts can in practice be achieved as

▶ feature fusion

or score fusion. In addition to these, one can also

discern data fusion, e.g. stereo images of a face, and

decision fusion, e.g. the decisions of several experts

wherein each expresses either of the crisp opinions

‘‘client’’ or ‘‘

▶ impostor,’’ in the taxonomy of fusion

[1]. However, one can see data fusion and decision

fusion as adding novel experts and as a special case of

score fusion, respectively. On the other hand, feature

fusion is often achieved as concatenation of feature

vectors, which is in turn modeled by an expert suitable

for the processing demands of the set of the novel

vectors. For this reason we only discuss score fusion

in this article. The initial frameworks for fusion have

been simplistic in that no knowledge on the skills of

the experts is used by the

▶ super visor. Later efforts

to reconcile different expert opinions in a multiple

experts biometric system have been described from

a probabilistic opinion modeling [2] and a pattern

discrimination [3], view points, respectively. From

both perspectives, it can be concluded that the weight-

ed average is a good way of reconciling different

authenticity scores of individual exp erts to a single

opinion, under reasonable conditions. As the weights

reﬂect the skills of the exper ts, some sort of training is

needed to esti mate them. Belonging to probabilistic

modeling school, respective discriminant analysis

school, Bayesian modeling [4, 5], and support vector

machines [6–8 ] have been utilized to fuse expert opi-

nions. An important issue for a fusion method is,

however, whether or not it has mechanisms to discern

the general skill of an expert from the quality of the

current data. We summarize the basic principles to

exemplify typical fusion approaches as follows.

Simple Fusion

This type of fusion applies a rule to input opinions

delivered by the experts. The rule is not obtained by

986

Multiple Classifiers

training on expert opinions, but are decided by the

designer of the supervisor. Assuming that the supervi-

sor receives all expert inputs in parallel, common sim-

ple fusions include,

where M

is the score output by the supervisor

at the instant of operation j, when m expert opinions,

expressed as real numbers x

i,j

,i :1...m, are available to

it. In addition to a parallel application of a single

simple fusion to all expert opinions, one can apply

several simple fusion rules serially (one after the

other) if some expert opinions are delayed before

they are processed by the supervisor(s).

Probabilistic Fusion

Experts can express opinions in various ways. The

simplest is to give a strict decision on a claim of an

identity, ‘‘1’’ (client) or ‘‘0’’ (impostor). A more com-

mon way is to give a graded opinion, usually a real

number in [0, 1]. However, it turns out that machine

experts can beneﬁt from a more complex representa-

tion of an opinion, an array of real variables. This is not

surprising to human experience because, a human

opinion is seldom so simple or lacks variability that it

can be described by what a single variable can afford.

A richer representation of an opinion is therefore the

use of the distribution of a score rather than a score.

Bayes theory is the natural choice in this case because it

is about how to update knowledge represented as dis-

tribution (prior) when new knowledge (likelihood)

becomes available.

Before describing a particular way of constructing a

Bayesian super visor let us illustrate the basic mecha-

nism of Bayesian updating. Let two stochastic variables

, X

represent these errors of two different measure-

ment systems measuring the same physical quantity.

We assume that these errors are independent and

are distributed normally as N(0, s

), N(0, s

), respec-

tively. Then their weighted average

M ¼ q

þ q

; where q

þ q

¼ 1 ð1Þ

is also normally distributed with N(0, q

þ q

Given the variances s

, s

, if the weights q

are

chosen inversely proportional to the respective var-

iances, the variance of the new variable M (the weighted

mean) will be smallest provided that

; q

ð2Þ

where inverse-proportionality constants (the denomi-

nators) ensure q

þ q

¼ 1. Notice that the composite

variable M is normally distributed always if the X

, X

are independent but the variance is smallest only for a

particular choice, (seen earlier) yielding

varðMÞ¼q

þq

 minðs

; s

Þð3Þ

The fact that the composite variance never exceeds the

smallest of the component variances, and that it con-

verges to the smallest of the two when either becomes

large, i.e. one distribution approaches the noninforma-

tive distribution N(0, 1), can be exploited to improve

the precision of the aggregated measurements, Fig. 1.

Appropriate weighting is the main mechanism on

how knowledge as represented by distributions can be

utilized to improve biometric decision making. Bayes

theory comes handy at this point because it offers the

powerful Bayes theorem to estimate the weights for the

aggregation of the distributions, incrementally, or at one-

go as new knowledge becomes available. We follow [4]to

max

min

sum

median

Product

Maximum of the scores,

Minimum of the scores,

Arithmetic mean of the scores,

Median of the scores,

Geometric mean of the scores,

¼ maxðx

1;j

; x

2;j

; ...; x

m;j

¼ minðx

1;j

; x

2;j

; ...; x

m;j

i¼1

i;j

¼ x

mþ1



¼ð

i¼1

i;j

Multiple Experts. Figure 1 The component distributions

with X

N(0,1), X

N(0,1.3

) and the composite

distribution M N(0,1∕(1.3

2

þ1)), (1).

Multiple Experts

987

exemplify the Bayesian approach. Let the following list

describe the variables representing the signals made

available by a multiexpert biometric system specialized

in making decisions. Next we will discuss the errors of

the experts on client and impostor data separately.

One can model the errors (not the scores) that

a speciﬁc expert makes when it encounters clients.

To this end, assume that Y

¼1 and that the conditional

stochastic variable Z

given its expectation value

is normally distributed i.e. (Z

)N(b

). If Z

are independent then, according to Bayes theory, the

posterior distribution (b

), will also be normal

ðb

ÞNðM

; V

Þð4Þ

with mean and variance

j¼1

and V

1

ð5Þ

respectively. In this updating, we see the same pattern

as in the example, (1–3). Here C is a label that

denotes that the applicable variables relate to clients.

This distribution at hand, one can now estimate b

the expectation of (b

) which is M

. This derivation

can be seen as that we updated a noninformative prior

distribution, b

2N(0, 1), i.e. ‘‘nothing is known about

’’ to obtain the posterior distribution (b

) 2 N

, V

). The resulting distribution is a Gaussian

function which attempts to capture the bias of each

expert, as well as the precision of each expert, which

together represent its skills.

We proceed next to use the observed knowledge

about an expert to obtain an unbiased estimate of its

score distribution at the time instant j ¼ n

.Byre-

applying Bayes theorem to update the distribution

given in (4) one obtains that,

ðY

i;1

; z

i;2

; :::; z

i;n

; x

i;n

Þ2NðM

; V

Þð6Þ

with mean and variance

¼ x

i;n

þ M

and V

¼ V

þ s

i;n

: ð7Þ

Consider now the situ ation that m independent

experts have delivered their authenticity scores on

supervisor-training shots (j ¼ 1, 2, ...,n

) and the test

shot n

. Using the Bayesian updating again, the

posterior distribution of b

, given the scores at the

instant j ¼ n

and the earlier errors, is normal;

ðY

1;1

; :::; z

1;n

; x

1;n

; :::; z

m;1

; :::z

m;n

; x

m;n

2 N ðM

; V

ð8Þ

where

i¼1

and V

i¼1

1

ð9Þ

However, to compute these means and variances,

the score variances s

are needed. We suppose that

these estimations are delivered by experts depending

on, e.g. the quality of the current biometric sample

underlying their scores. This is reasonable because not

all samples have the same (good) quality, inﬂuencing

the precision of the observed score x

. In case this is

not practicable for various reasons, one can assume

that x

has the same variance within an expert i (but

allow it to vary between experts). Then, the variances

of the distributions of x

need not be delivered to the

supervisor, but can be estimated by the supervisor, as

discussed in the following section. Before one can use

the distribution N(M

, V

) as a supervisor, one

needs to compare it with the distribution obtained by

an alternative aggregation.

Assume now that we perform this training with n

impostor samples (Y

¼ 0) i.e. that we compute the

bias distribution N(M

, V

) when expert i evaluates

impostors, and the ﬁnal distribution N(M

, V

), with

I being a label denoting ‘‘Impostor.’’ We do not write

the update formulas explicitly as these are identical

Index of the experts. i 2 1...m,

Index of shots (one or more per candidate), j 2

1...n, n

. It is equivalent to time since an expert

has one shot per evaluation time (period). The

time n is the last instant in the training whereas

is the test time when the system is in

operation.

The authenticity score, i.e. the score delivered by

expert i on shot j ’s claim of being a certain client

The true authenticit y score of shot j’s claim being

a certain client. This variable can take only two

numerical values corresponding to ‘‘True’’ and

‘‘False’’

The miss-identification score, that is Z

¼ Y

X

The variance of Z

as estimated by expert i

988

Multiple Experts

to (5,7,9) except that the training set consists of impos-

tors. One of the two distributions N(M

, V

), and N

, V

), represents the true knowledge better than

the other at the test occasion, j ¼ n

. At this point one

can choose the distribution that achieves a resemblance

that is most bona-ﬁde to its role, e.g.

; if 1  M

 M

;

; otherwise:



ð10Þ

In other words if the client-supervisor has a mean

closer to its goal (one, because Y

¼1 represents client)

than the impostor-supervisor’s mean is to its goal

(zero) then the choice falls on the distribution coming

from the client-supervisor and vice-versa. An addi-

tional possibility is to reject to output a distribution

in case the two competing distributions overlap

more than a desired threshold. One could also think

of a hypersupervisor to reconcile the two antagonist

▶ super visor opinions.

In practice most experts deliver scores that are

between 0 and 1. However, there is a formal incompat-

ibility of this with our assumptions because the dis-

tributions of Z

would be limited to the interval [1,1]

whereas the concept we discussed earlier is based on

normal distributions taking values in] 1, 1[. This

is a classical problem in statistics and is addressed

typically by remapping the scores so that one works

with ‘‘odds’’ of scores

¼ log

1  X

ð11Þ

where X

2 ]0,1[. It can be shown that the supervisor

formula (10) and its underlying updating formulas

hold for X

as well. The only difference is in the con-

ditional distributions which will be log normal yield-

ing, in particular, the expected value exp(M

þV

∕2)

and the variance exp(2M

þ 2V

)exp(2M

þV

) for

, (8).

Quality estimations for Bayesian supervisors. There

are various ways to estimate the variance of a score

distribution associated with a particular biometric

sample on which an expert expresses an opinion of

authenticity. A Bayesian supervisor expects this esti-

mate because it works with distributions to represent

the knowledge/opinion concerning the current sample

as well as the past experience, not scalars. It makes

most sense that this information is delivered by the

expert or by considering the quality of the score. Next

we discuss how these can be entered into update

formulas.

One can assume that the experts give the precisions

correctly except for an individual proportionality

constant.

¼ a

ð12Þ

Applying the Bayes theory again, i.e. a

is ﬁrst modeled

to be a distribution rather than a scalar, then the

distribution of (a

j(z

i,1

),...,(z

i,n

)) can be com-

puted (it is a beta distribution under reasonable

assumptions [4]). In turn this allows one to estimate

the conditional expectation of

, yielding a Bayesian

estimate of the score-error variances



i;j

¼ Eðs

; ðz

i;1

; s

i;1

Þ; ðz

i;n

; s

i;n

ÞÞ

¼ s



¼ s

ðG

 D

n  3

ð13Þ

with

¼ E



ðG

 D

n  3

; G

j¼1

and

j¼1



j¼1



1

ð14Þ

Note that, n will normally represent the number of

biometric samples in the training set and equals to

either n

or n

. From this result it can also be con-

cluded that if an expert is unable to give a differen-

tiated quality estimation then its variance estimation s

will be constant across the biometric samples it

inspects and the



will approach gracefully to the

variance of the error of the scores of the expert (not

adjusted to sample quality).

The machine expert will, in practice, be allowed to

deliver an empirical quality score p

because these are

easier to obtain than variance estimations, s

. At this

point, one can assert that these qualities are inversely

proportional to the underlying standard deviations of

the score distributions, yielding

ð15Þ

where p

is a quality measure of the biometric sample j

as estimated by the expert i . If it is a human exper t that

estimates the quality p

it can be the length of the

interval in which she/he is willing to place the score

, so that even human and machine opinions can be

reconciled by using the Bayesian supervisor. In Fig. 2 (a),

Multiple Experts

989