Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

calibration or 3D reconstruction. Other application

domains include pose estimation, image alignment,

or mosaicing. A t ypical example here is the features

used in the KLT tracker [1]. Finally, a set of local

features can be used as a robust image representation,

that allows to recognize objects or scenes without the

need for segmentation. Here again, it does not really

matter what the features actually represent. They do

not even have to be localized precisely, since the goal is

not to match them on an individual basis, but rather to

analyze their statistics. This way of exploiting local

features was ﬁrst reported in the seminal work of [2]

and soon became very popular, especially in the con-

text of object recognition (both for speciﬁc objects as

well as for category-level recognition). Other applica-

tion domains include scene classiﬁcation, texture anal-

ysis, image retrieval, and video mining.

Introduction

The ﬁrst publication on local features appeared after

the observation on the importance of corners and

junctions in visual recognition [3] (see Fig. 1). Since

then a large number of algorithms have been suggested

for extracting

▶ interest points at the extrema of vari-

ous functions computed on the digita l shape. Also, it

has been understood early on in the image processing

and visual pattern recognition ﬁeld that intersections

of straight lines and straight corners are strong indic a-

tions of man made structures. Such features have been

used in the ﬁrst series of applications from line draw-

ing images [4] and photomosaics [5]. First mono-

graphs on digital image processing [6, 7] and later

editions served to establish the ﬁeld on a sound theo-

retical foundation. Several survey articles on local fea-

tures appeared recently [8–10].

Interest points are now the preferred strategy for

solving a wide variety of problems, from wide baseline

matching and the recognition of speciﬁc objects to the

recognition of object classes. Additionally, similar ideas

have been applied to texture recognition, scene classi-

ﬁcation, robot nav igation, visual data mining, and

symmetry detection, to name just a few application

domains.

Local

▶ invariant features not only allow to ﬁnd

correspondences, in spite of large changes in viewing

conditions, occlusions, and image clutter (wide base-

line matching), but also yield an interesting descrip-

tion of the image content for image retrieval and object

or scene recognition tasks (both for speciﬁc objects as

well as categories). To put this into context, some

alternative strategies are brieﬂy summarized, including

global features, image segments, and exhaustive and

random sampling of features.

Global Features

In the ﬁeld of image retrieval, many global features

have been proposed to describe the image content,

with color histograms and variations thereof as a

Local Image Features. Figure 1 Illustration of local features in line drawing images and a grayvalue image.

940

Local Image Features

typical example [11]. This approach works surprisingly

well, at least for images with distinctive colors, as long

as it is the overall composition of the image as a whole

that the user is interested in, rather than the fore-

ground object. Indeed, global features cannot distin-

guish foreground from background, and mix

information from both parts together.

Global features have also been used for object rec-

ognition, resulting in the ﬁrst appearance-based

approaches to tackle this challenging problem. [12]

and later [13] proposed to compute a principal com-

ponent analysis of a set of model images and to use the

projections onto the ﬁrst few principal components as

descriptors. Compared to the purely geometry-based

approaches tried before, the results of the novel ap-

pearance-based approach were striking. A whole new

range of natural objects could suddenly be recognized.

However, being based on a global description, image

clutter and occlusions again form a major problem,

limiting the usefulness of the system to cases with clean

backgrounds or where the object can be segmented

out, e.g., relying on motion information.

Image Segments

An approach to overcome the limitations of the global

features is to segment the image in a limited number

of regions or segments, with each such region

corresponding to a single object or a part thereof.

However, this raises a chicken-and-egg problem as

image segmentation is a very challenging problem in

itself, which in general requires a high-level under-

standing of the image content. For generic objects,

color and texture cues are insufﬁcient to obtain mean-

ingful segmentations.

Sampled Features

A way to deal with the problems encountered with

global features or image segmentation is to exhaustively

sample different subparts of the image at each location

and scale. For each such image subpart, global features

can then be computed. This approach is also referred

to as a sliding window based approach. It has been

especially popular in the context of face detection,

but has also been applied for the recognition of speciﬁc

objects or particular object classes such as pedestrians

or cars.

By focusing on subparts of the image, these meth-

ods are able to ﬁnd similarities between the queries and

the models in spite of changing backgrounds, even if

the object covers only a small percentage of the total

image area. In the bottom, they still do not manage to

cope with partial occlusions, and the allowed shape

variability is smaller than what is feasible with a local

feature based approach. However, by far the biggest

drawback is the inefﬁciency of this approach. Each and

every subpart of the image must be analyzed, resulting

in thousands or even millions of features per image.

This requires extremely efﬁcient methods which signif-

icantly limits the scope of possible applications. To

overcome the complexity problems sparser ﬁxed grid

sampling of image patches can be used. It is however

difﬁcult to achieve invariance to geometric deforma -

tions for such features. The approach can tolerate some

deformations due to dense sampling over possible

locations, scales, poses etc. but the individual features

are not invariant. As a result, sampled features cannot

be used when the goal is to ﬁnd precise corres-

pondences between images. However, for some app-

licationssuchassceneclassiﬁcationortexture

recognition, they may well be sufﬁcient.

In a similar vein, rather than using a ﬁxed grid of

patches, a random sampling of image patches can also

be used. This gives a larger ﬂexibility in the number of

patches, the range of scales or shapes, and their spatial

distribution. Random patches are in fact a subset of the

dense patches, and are used mostly to reduce the com-

plexity. Their repeatability is poor hence they work

better as an addition to the regular features rather

than as a stand alone method.

Finally, to overcome the complexity problems

while still providing a large number of features with

better than random localization one can sample fea-

tures uniformly from edges. This proved useful for

dealing with wiry objects well represented by edges

and curves.

Properties of the Ideal Local Feature

Local features typically have a spatial extent, i.e., the

local neighborhood of pixels ment ioned above. In con-

trast to classical segmentation, this can be any subset of

an image. The region boundaries do not have to corre-

spond to the changes in image appearance such as

color or texture. Also, multiple regions may overlap,

Local Image Features

941

and ‘‘uninteresting’’ parts of the image such as homo-

geneous areas can remain uncovered.

Ideally, one would like such local features to corre-

spond to semantically meaningful object parts. In

practice, however, this is unfeasible, as this would

require high-level interpretation of the scene content,

which is not available at this early stage. Instead, detec-

tors select local features directly based on the underly-

ing intensity patterns.

Good features should have the following

properties:



Repeatability: Given two images of the same object

or scene, taken und er different viewing conditions,

a high percentage of the features detected on the

scene part visible in both images should be found

in both images.



Distinctiveness/informativeness: The intensity pat-

terns underlying the detected features should

show a lot of variation, such that features can be

distinguished and matched.



Locality: The features should be local, so as to

reduce the probability of occlusion and to allow

simple model approximations of the geometric and

photometric deformations between two images

taken under different viewing conditions (e.g.,

based on a local planarity assumption).



Quantity: The number of detected features should

be sufﬁciently large, such that a reasonable number

of features are detected even on small objects. How-

ever, the optimal number of features depends on

the application. Ideally, the number of detected

features should be controllable over a large range

by a simple and intuitive threshold. The density

of features should reﬂect the information con-

tent of the image t o provide a compact image

representation.



Accuracy: The detected features should be accu-

rately localized, in both image location, with re-

spect to scale and possibly shape.



Efﬁciency: Preferably, the detection of features

in a new image should allow for time-critical

applications.

Repeatability, arguably the most important

property of all, can be achieved in two different

ways: either by invariance or by robustness.



Invariance: When large deformations are to be

expected, the preferred approach is to model these

mathematically if possible, and then develop

methods for feature detection that are unaffected

by these mathematical transformations.



Robustness: In case of relatively small deformations,

it often sufﬁces to make feature detection methods

less sensitive to such deformations, i.e., the accu-

racy of the detection may decrease, bu t not drasti-

cally. Typical deformations that are tackled using

robustness are image noise, discretization effects,

compression artifacts, blur, etc. Also geometric and

photometric deviations from the mathematical

model used to obtain invariance are often over-

come by including more robustness.

Clearly, the importance of these different properties

depends on the actual application and settings, and

compromises need to be made.

Repeatability is required in all application scenarios

and it directly depends on the other properties like

invariance, robustness, quantity etc. Depending on

the application, increasing or decreasing them may

result in higher repeatability.

Distinctiveness and locality are competing proper-

ties and cannot be fulﬁlled simultaneously: the more

local a feature, the less information is available in

the underlying intensity pattern and the harder it

becomes to match it correctly, especially in database

applications where there are many candidate features

to match to. On the other hand, in case of planar

objects and/or purely rotating cameras (e.g., in image

mosaicing applications), images are related by a global

homography, and there are no problems with occlu-

sions or depth discontinuities. Under these conditions,

the size of the local features can be increased without

problems, resulting in a higher distinctiveness.

Similarly, an increased level of invariance typically

leads to a reduced distinctiveness, as some of the image

measurements are used to lift the degrees of freedom of

the transformation. A similar rule holds for robustness

versus distinctiveness, as typically some information is

disregarded (considered as noise) to achieve robust-

ness. As a result, it is important to have a clear idea on

the required level of invariance or robustness for a

given application. It is hard to achieve high invariance

and robustness at the same time and invariance, which

is not adapted to the application, may have a negative

impact on the results.

Accuracy is especially important in wide baseline

matching, registration, and structure from motion

applications, where precise correspondences are

942

Local Image Features

needed to, e.g., estimate the epipolar geometry or to

calibrate the camera setup.

Quantity is particularly useful in some class-le vel

object or scene recognition methods, where it is vital to

densely cover the object of interest. On the other hand,

a high number of features have in most cases a negative

impact on the computation time and it should be kept

within limits. Also robustness is essential for object

class recognition, as it is impossible to model the

intra-class variations mathematically, so full invariance

is impossible. For these applications, an accurate local-

ization is less important. The effect of inaccurate

localization of a feature detector can be countered, up

to some point, by having an extra robust descriptor,

which yields a feature vector that is not affected by

small localization errors.

Related Entries

▶ Gabor ﬁlter

▶ Image descriptors

▶ Local binary pattern

▶ Local Feature Filters

▶ Matching

▶ Registration

References

1. Shi, J., Tomasi, C.: ‘‘Good features to track,’’ in: Proceedings of

the Conference on Computer Vision and Pattern Recognition,

pp. 593–600 (1994)

2. Schmid, C., Mohr, R.: Local gray-value invariants for image re-

trieval. IEEE Trans. Pattern Anal. Mach. Intell. 19(5), 530–534

(1997)

3. Attneave, F.: Some informational aspects of visual perception.

Psychol. Rev. 61, 183–193 (1954)

4. Freeman, H.: A review of relevant problems in the processing of

line-drawing data, AII, pp. 155–174 (1969)

5. Milgram, D.: Computer methods for creating photomosaics.

IEEE Trans. Comput. 23 , 1113–1119 (1975)

6. Duda, R., Hart, P.: Pattern Classiﬁcation and Scene Analysis.

Wiley, New York (1973)

7. Rosenfeld, A.: Picture processing by computer. ACM Comput.

Surv. 1(3), 147–176 (1969)

8. Mikolajczyk, K., Schmid, C.: A performance evaluation of local

descriptors. IEEE Trans. Pattern Anal. Mach. Intell. (2005)

9. Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., Gool, L.V.: A comparison

of afﬁne region detectors. Int. J. Comput. Vis. (2005)

10. Tuytelaars, T., Mikolajczyk, K.: Local Invariant Feature

Detectors: A Survey, Foundations and Trends in Computer

Graphics and Vision (2008)

11. Swain M., Ballard, D.: Color indexing. Int. J. Comput. Vis. 7(1),

11–32 (1991)

12. Turk, M.A., Pentland, A.P.: Eigenfaces for face recognition,

in The Conference on Computer Vision and Pattern Recognition,

pp. 586–591 (1991)

13. Murase, H., Nayar, S.: Visual learning and recognition of

3D objects from appearance. Int. J. Comput. Vis. 14(1), 5–24

(1995)

Local Image Filters

ABDENOUR HADID,MATTI PIETIKA

INEN

Machine Vision Group, Department of Electri cal and

Information Engineering, University of Oulu, Finland

Synonyms

Gabor features; LBP features

Definition

Local feature ﬁlters can be deﬁned as operators (or

ﬁlters) which are applied to an image in order to

extract local characteristics describing (some) impor-

tant information in the image. For instance, these

characteristics (or

▶ features) can be used to detect,

recognize, and analyze the objects in the image. They

can also facilitate the interpretation or further proces-

sing of the image. In contrast to global features which

describe the overall content and shape of the objects in

the image, local features deﬁne speciﬁc information in

local regions. Among the most effective operators for

feature extractio n are Gabor ﬁlter and local binary

pattern (LBP). Gabor ﬁlters are linear bandpass ﬁlters

computed for images at different orientations and

scales. The imp ulse response of a Gabor ﬁlter is deﬁned

by a harmonic function multiplied by a Gaussian func-

tion. Local binary pattern is a nonlinear operator

which labels the pixels of an image by thresholding

the neighborhood of each pixel with the value of the

center pixel and considers the result as a binary num-

ber. LBP labels can be regarded as local primitives such

as curved edges, spots, ﬂat areas, etc. The histogram of

Local Image Filters

943

the labe ls can be then used as a feature vector (or image

representation). Gabor ﬁltering and LBP operator are

powerful means of analyzing biometric data such faces,

irises, ﬁngerprints, palmprints, etc.

Introduction

Typically, biometric systems operate by acquiring bio-

metric data from which features are extracted and

matched against those of the templates which are

stored in the database [1]. This involves two crucial

aspects: feature extraction and classiﬁer design. The

aim of feature extraction is to ﬁnd good descriptors

which are easy to compute and have high

▶ extra-class

variance (i.e., between different persons) and low

▶ intra-class variance, w hich means that the descriptor

should be robust with respect to aging of the subjects,

alternating illumination and other factors. Obviously,

if inadequate features are adopted, even the most so-

phisticated classiﬁers (i.e., comparison schemes) will

fail to accomplish the given recognition task. There-

fore, feature extraction is a very important task in any

biometric system.

Different global (or ho listic) methods such as Prin-

cipal Component Analysis (PCA) have been widely

studied and applied to biometrics but lately local

features have gained more attention due to their ro-

bustness to challenges such as pose and illumination

changes. In this context, feature extraction using

Gabor ﬁltering or LBP has gained increasing attention

in various biometric applications. A notable example

is iris recognition, in which approaches based on

multichannel Gabor ﬁltering have been highly success-

ful. Gabor ﬁlters have also been widely used, e.g., in

ﬁngerprint [2] and palmprint analysis [3]. Also, the

well-known Elastic Bunch Graph Matching (EBGM)

method is based on Gabor ﬁlter responses at certain

ﬁducial points to recognize faces [4]. More recently,

LBP features have provided excellent results in various

biometric applications [5, 6, 7, 8]. Perhaps the most

important property of the LBP operator in real-world

applications is its robustness to mono tonic gray-scale

changes caused, for example, by illumination varia-

tions. Another important property is its computation-

al simplicity, which makes it possi ble to analyze

biometric data in challenging real-time settings.

The Gabor and LBP methods provide complemen-

tar y information for analysis: LBP captures small

and ﬁne details (or micro features) while Gabor ﬁlters

encode appearance information over a broader range

of scales (macro features).

Gabor Filters

The theory behind Gabor ﬁlters started from the original

work of Dennis Gabor who proposed in 1946 to repre-

sent signals as a combination of elementary functions

[9]. Those particular elementary functions are now

known as Gabor elementary functions (GEF). How-

ever, the use of Gabor ﬁlters in image processing

started from the work of Granlund who extended the

elementary 1-d Gabor functions to 2-d elementary

functions and used them in the development of a

general picture processing operator [10]. Later, Daug -

man proposed the generalization of 1-d gabor func-

tions to two dimensions and importantly showed the

equivalence between a structure based on the 2-d

Gabor functions and the organization and the charac-

teristics of the mammalian visual system [11]. These

physiological ﬁndings are undoubtedly behind the

great impact of Gabor research especially in image

processing.

Roughly speaking, Gabor ﬁltering in image proces-

sing consists of applying a set of 2-d Gabor elementary

functions of various parameters (e.g., different di la-

tions and rotations) to an input image thus obtaining

Gabor image features (i.e., feature space). These

extracted Gabor features can be then used directly as

feature vectors for analysis (e.g ., biometric recogni-

tion) or can ﬁrst be transformed into new feature

vectors (e.g ., [8]). So, typically, an input image I(x, y)

is convolved with a 2-d Gabor function g(x,y) to ob-

tain a Gabor feature image r(x, y) as follows:

rðx; yÞ¼Iðx; yÞgðx; yÞ

þ1

1

Iðdx; dÞgðx  dx; y  dÞ dx d:

There are several forms of Gabor elementary functions

(GEFs) which can be designed to be highly selective in

frequency w hile displaying good spatial localization.

GEFs can be also seen as bandpass ﬁlters which can

be conﬁgured to be used for feature extraction. A GEF

is deﬁned as a Gaussian modulated by a sinusoid

(cosine function) as follows:

944

Local Image Filters

l;y;c;s;g

ðx; yÞ¼expð

þ g

cosð2p

þ cÞ;

where x

¼ x cos y þ y sin y, y

¼x sin y þ y cos y,

l represents the wavelength of the cosine factor, y

represents the orientation of the normal to the parallel

stripes of a Gabor function, c is the phase offset,

s refers to the variance of the Gaussian function and

g is the spatial aspect ratio and speciﬁes the ellipticity

of the support of the Gabor function. Figure 1 shows

an example of a typical 2-d Gabor ﬁlter.

Local Binary Patterns

The LBP texture analysis operator [ 12], introduced by

Ojala et al., is deﬁned as a gray-scale invariant texture

measure, derived from a general deﬁnition of texture in

a local neighborhood. It is a powerful means of texture

description and among its properties in real-world

applications are its discriminative power, computa-

tional simplicit y, and tolerance against monotonic

gray-scale changes. The original LBP operator forms

labels for the image pixels by thresholding the 3  3

neighborhood of each pixel with the center value and

considering the result as a binary num ber. The histo-

gram of these 2

¼256 different labels can then be used

as a texture descriptor.

The operator has been extended to use neigbor-

hoods of different sizes [13]. Using a circular neighbor-

hood and bilinearly interpolating values at noninteger

pixel coordinates allows any radius and number of

pixels in the neighborhood. The notation (P, R)is

generally used for pixel neighborhoods to refer to P

sampling points on a circle of radius R. The calculation

of the LBP codes can be easily done in a single scan

through the image. See Fig. 2 for an illustration of the

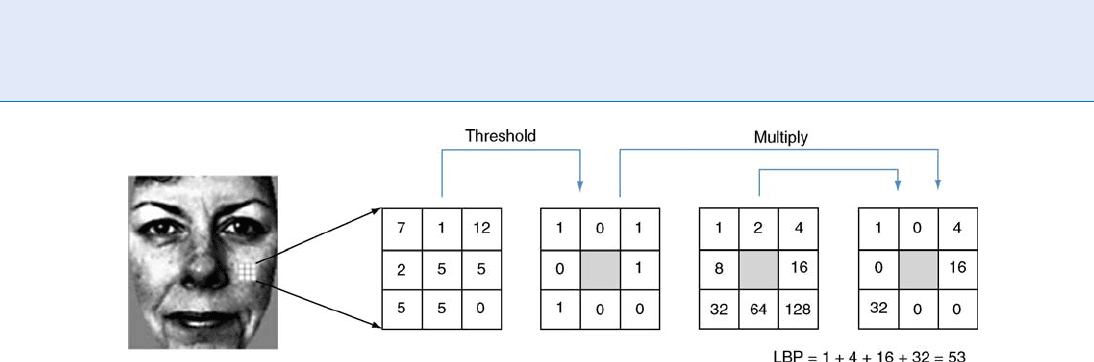
basic LBP operator. The value of the LBP code of a

pixel (x

, y

) is given by LBP

P;R

P1

p¼0

 g



where g

corresponds to the gray value of the center

pixel (x

, y

), g

refers to gray values of P equally spaced

pixels on a circle of radius R, and s deﬁnes a threshold-

ing function as follows:

sðxÞ¼

1; if x  0;

0; otherwise:



Another extension to the original operator is the

deﬁnition of so called uniform patterns [13]. This ex-

tension was inspired by the fact that some binary

patterns occur more commonly in texture images

than in others. A local binary pattern is called uniform

if the binary pattern contains at most two bitwise

transitions from 0 to 1 or vice versa when the bit

pattern is traversed circularly. For example, the patterns

00000000 (0 tr ansitions), 01110000 (2 transitions),

Local Image Filters. Figure 1 An example of a typical 2-d Gabor filter.

Local Image Filters

945

and 11001111 (2 transitions) are uniform whereas the

patterns 11001001 (4 transitions) and 01010011

(6 transitions) are not. In the computation of the

LBP labels, uniform patterns are used so that there is

a separate label for each uniform pattern and all the

nonuniform patterns are labeled with a single label.

For example, when using (8, R) neighborhood, there

are a total of 256 patterns, 58 of which are uniform,

which yields 59 different labels. This yields the follow-

ing notation for the LBP operator: LBP

P,R

. The sub-

script represents using the operator in a (P, R)

neighborhood. Superscript u2 stands for using only

uniform patterns and labeling all remaining patterns

with a single label. Each bin (LBP label) can be

regarded as a microtexton. Local primitives which are

codiﬁed by these bins include different types of curved

edges, spots, ﬂat areas, etc.

The original LBP operator was deﬁned to only deal

with spatial information. Recently, it has been extend-

ed to a spatiotemporal representation for dynamic

texture analysis. This has yielded the so called Volume

Local Binary Pattern operator (VLBP) [6]. The idea

behind VLBP consists of looking at dynamic texture as

a set of volumes in the (X,Y, T) space where X and Y

denote the spatial coordinates and T denotes the frame

index (time). The neighborhood of each pixel is thus

deﬁned in three dimensional space. Then, similar to

LBP in spatial domain, volume textons can be deﬁned

and extracted into histograms. Therefore, VLBP com-

bines motion and appearance together to describe

dynamic texture. Later, to make the VLBP compu ta-

tionally simple and easy to extend, the cooccurrences

of the LBP on three orthogonal planes (LBP-TOP)

were also introduced [6]. LBP-TOP consists then in

considering three orthogona l planes: XY , XT, and YT,

and concatenating local binary pattern cooccurrence

statistics in these three directions. The circular

neighborhoods are generalized to elliptical sampling

to ﬁt to the space-time statistics.

In the LBP approach to texture classiﬁcation [13],

the occurrences of the LBP codes in an image are

collected into a histogram. The classiﬁcation is then

performed by computing simple histogram similari-

ties. However, considering a similar approach for bio-

metric (e.g., facial) image representation results in a

loss of spatial information and therefore one should

codify the texture information while retaining also

their locations. One way to achieve this goal using

texture operators is to build several local descriptions

of the face and combine them into a global description

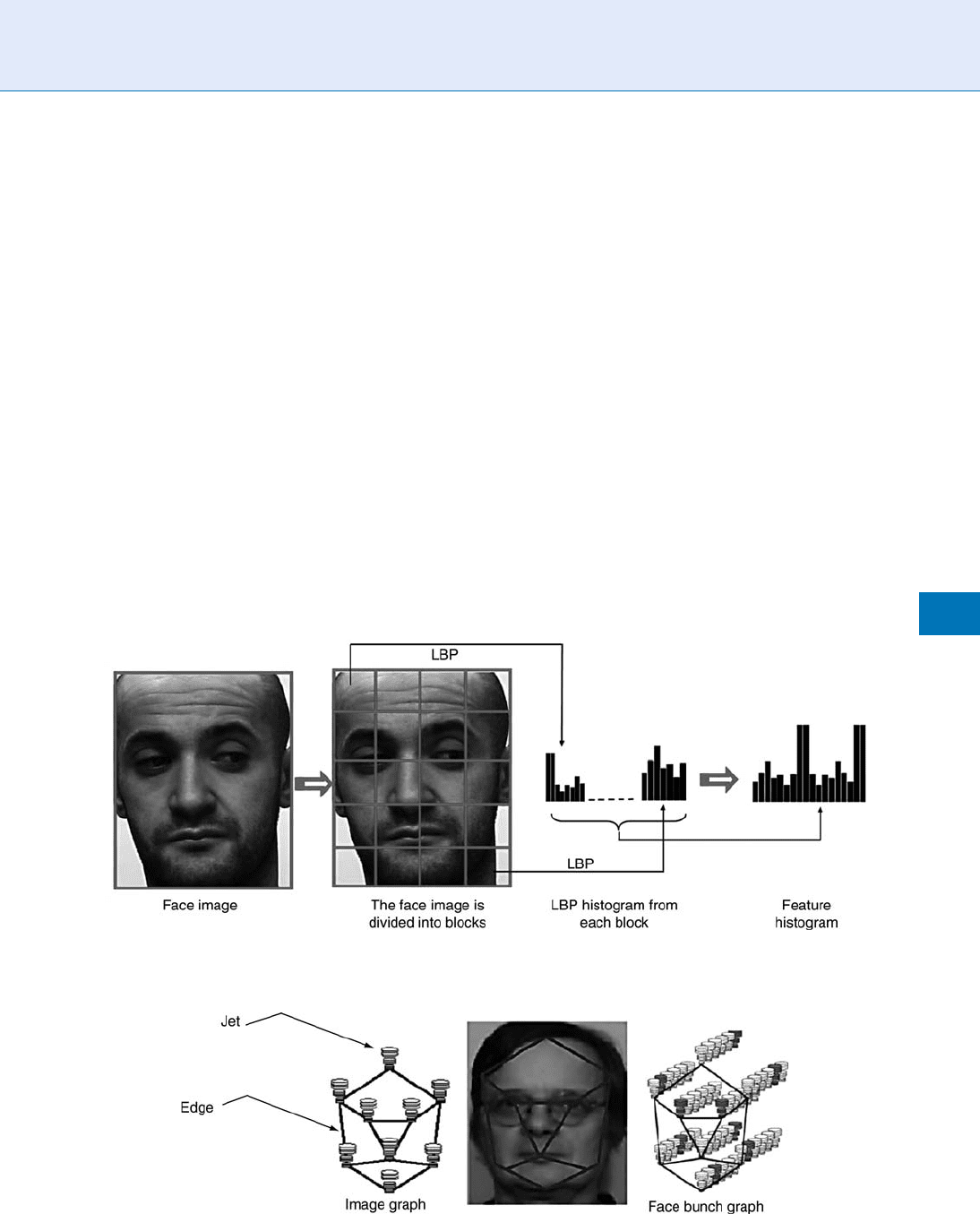
[5, 8]. Figure 3 shows an example of an LBP based

facial representation. Such local descriptor based

methods have been gaining interest lately which is

understandable given the limitations of the holistic

representations. These local feature based methods

seem to be more robust against variations in pose or

illumination than holistic methods.

Applications

There is a considerable amount of research concerning

Gabor ﬁltering based biometric recognition, especially

in iris, face, ﬁngerprint, and plamprint recognition

[1, 14, 2, 15, 4, 3]. For instance, Daugman developed

the pioneering approach to iris recognition [14]. He

used 2-d Gabor ﬁltering to extract local texture fea-

tures from iris images, resulting in an IrisCode repre-

sentation with 2,048bits. Then, the recognition was

done simply by computing the Hamming distance

between a pair of iris representations. The system was

tested on billions of iris images and the results showed

excellent recognition rates very close to 100% (only

one false acceptance in 151,000 imposter tests for one

Local Image Filters. Figure 2 The basic LBP operator.

946

Local Image Filters

false rejection in 128,000 tests). Nowadays, many com-

mercial iris-recognition systems are based on Daug-

man’s algorithms.

Gabor ﬁlter based features have also been widely

applied to ﬁngerprint recognition systems. A notable

example is the system developed by Jain [2] using a

bank of Gabor ﬁlters to capture both the global pattern

of ridges and valleys and the local characteristic s

in ﬁngerprint patterns yielding feature vectors called

FingerCodes. The ﬁngerprint matching is based on

the Euclidean distance between two corresponding

FingerCodes. The system achieved remarkable recog-

nition rates.

In face recognition, Lades et al. developed a Gabor

based system using dynamic link a rchitectu re (DLA)

framework which recognizes faces by extracting Gabor

jets at each node of a rectangular grid over the face

image [15]. Later, Wiskott et al. extended the approach

and developed the well-know n Gabor wavelet-based

elastic bunch graph matching (EBGM) method to

label and recognize faces [4]. In the EBGM algorithm,

faces are represented as grap hs with nodes positioned

at ﬁducial points (such as the eyes, the tip of the nose,

etc.) and edges labeled with distance vectors (see

Fig. 4). Each node contains a set of Gabor wavelet

coefﬁcients, known as a jet. Thus, the geometry of the

face is encoded by the edges while the gray value

distribution (texture) is encoded by the jets. The iden-

tiﬁcation of a new face consists of determining among

the constructed graphs the one which maximizes the

graph similarity function.

In palmprint recognition, for instance, Zhang et al.

[3] proposed the use of 2-d Gabor phase encoding

scheme for palmprint feature extraction and represen-

tation. First, the central areas from palmprint images

are segmented and then 2-d Gabor based features are

extracted. The recognition is performed using normal-

ized Hamming distance. Experiments on a database of

7,752 low resolution palmprint images showed good

performance. It is worth nothing that the use of Gabor

ﬁltering in biometrics is not limited to the examples

cited earlier as many other Gabor based biometric

Local Image Filters. Figure 3 Example of an LBP based facial representation.

Local Image Filters. Figure 4 An example of facial representation with the elastic bunch graph principle (EBGM).

Local Image Filters

947

systems for commercial applications have been suc-

cessfully developed. In addition, Gabor features have

also been successfully used with other biometric mod-

alities including speech, gait, ear, etc.

LBP has also been successfully used in various

biometric applications such as face, activity, iris, and

palmprint recognition. The most remarkable applica-

tion of LB P in biometrics is face analysis [5]. The idea

consists in dividing the faces into several regions (or

blocks) from which the local binary pattern histograms

are computed and concatenated into a single, spatially

enhanced feature histogram (Fig. 3). In such a rep-

resentation, the texture of facial regions is encoded

by the LBP while the shape of the face is recovered by

the concatenation of different local histograms. The

LBP methodology has attained an established posi-

tion in face analysis research and several research

groups around the world have adopted similar ap-

proach to different tasks such as near-infrared based

face recognition, gender recognition, head pose esti-

mation and 3D face recognition. A bibliography of

LBP-related research in facial image analysis can be

found at http://www.ee.oulu.ﬁ/research/imag/texture/

lbp/bibliography/.

The spatiotemporal versions of LBP (VLBP and

LBP-TOP) have also been successfully applied to per-

son analysis and identiﬁcation from video sequences,

including face, facial expression, visual speech and

activity recognition. To recognize six prototypic emo-

tions (anger, disgust, fear, joy, sadness, and surprise)

from videos, Zhao et al. [6] divided the face sequences

into several overlapping block volumes, extracted LBP-

TOP (or VLBP) histograms from each block and then

concatenated them to obtain a single histogram repre-

senting the appearance and motion of the facial ex-

pression in the face seque nces. This approach does not

require error-prone segmentation of lips and other

facial features and it is robust against monotonic gray

scale changes caused, for example, by illumination and

skin color variations, and errors in face alignment.

Hadid et al. [7] also adopted spatiotemporal LBP for

face recognition from videos with excellent results.

Starting from the observation that VLBP features con-

sist of both intra and extra personal information

(corresponding to both facial expression a nd identity),

they proposed a robust recognition system using VLBP

with AdaBoost learning. The idea was to classify the

VLBP facial information into intra and extra classes,

and then use only the

▶ extra-class VLBP features for

recognition. This was achieved by looking at a face

sequence as a selected set of rectangular prisms

(volumes) from which local histograms of extended

VLBP code occurrences are extracted. Then, a boosting

approach is used for selecting only the most discrimi-

native spatiotemporal patterns for face recognition

while discarding the patterns which may hinder the

recognition process.

There are many other very successful biometric

applications based on Gabor ﬁltering or LBP features.

The approaches based on Gabor ﬁltering or wavelets

measuring the frequency contents of image points or

regions at different resolutions and orientations en-

code appearance information over a broad range of

scales (macro features) w hile LBP operat or captures

smaller and ﬁner details (or micro features). This

makes Gabor ﬁltering and LBP operator powerful

means for extracting complementary information. Tak-

ing this into account, one way to go ahead would be

to combine Gabor and LBP methods. Following this

direction, Zhang et al. proposed the so called Local

Gabor binary pattern histogram sequence (LGBPHS)

in which multiresolution and multiorientation descrip-

tion of an image using Gabor ﬁlters is ﬁrst computed,

and then LBP histograms are computed from the

Gabor features for small nonoverlapping regions and

concatenated into a feature histogram. Excellent results

are reported [8]. Other works have also successfully

exploited the complementary of Gabor ﬁlters and

LBP features by fusing the two sets of features for

recognition (see references at http://www.ee.oulu .ﬁ/

research/imag/texture/lbp/bibliography/).

Summary

Feature extraction is a very important and crucial task

in all biometric systems. In this context, Gabor ﬁl tering

and LBP operator are powerful means for extracting

complementary features and describing biometric data

such as faces, irises, ﬁngerprints, palm prints, etc. This

can be attested by the large number of successful bio-

metric applications based on these features. Gabor

ﬁlters are linear ban dpass ﬁlters computed for images

at di fferent orientations and scales while LBP is a

nonlinear operator codifying the relationship between

each center pixel and its neighborhood, thus describing

a set of local primitives such as curved edges, spots, ﬂat

areas, etc. In contrast to global features which describe

948

Local Image Filters

the overall content and shape of the objects in the

image, local features deﬁne speciﬁc information in

local regions. The local feature based methods seem to

be more robust against variations in pose or illumina-

tion than holistic methods.

Related Entries

▶ Classiﬁer Design

▶ Face Descriptors

▶ Feature Extraction

References

1. Jain, A.K., Ross, A., Prabhakar, S.: An introduction to biometric

recognition. IEEE Trans. Circuits Syst. Video Technol., Special

Issue on Image- and Video-Based Biometrics 14(1), 4–20 (2004)

2. Jain, A.K., Prabhakar, S., Hong, L., Pankanti, S.: Filterbank-

based ﬁngerprint matching. IEEE Trans. Image Process. 9(5),

846–859 (2000)

3. Zhang, D., Kong, W., You, J., Wong, M.: Online palmprint

identiﬁcation. IEEE Trans. Pattern Anal. Mach. Intell.

25(9),1041–1050 (2003)

4. Wiskott, L., Fellous, J.M., Kuiger, N., von der Malsburg, C.: Face

recognition by elastic bunch graph matching. IEEE Trans. Pat-

tern Anal. Mach. Intell. 19, 775–779 (1997)

5. Ahonen, T., Hadid, A., Pietika

inen, M.: Face description with

local binary patterns: application to face recognition. IEEE

Trans. Pattern Anal. Mach. Intell. 28(12), 2037–2041 (2006)

6. Zhao, G., Pietika

inen, M.: Dynamic texture recognition using

local binary patterns with an application to facial expressions.

IEEE Trans. Pattern Anal. Mach. Intell. 29(6), 915–928 (2007)

7. Hadid, A., Pietika

inen, M., Li, S.Z.: Learning personal speciﬁc

facial dynamics for face recognition from videos. In: Analysis

and Modeling of Faces and Gestures (AMFG 2007), Lecture

Notes in Computer Science, vol. 4778, pp. 1–15 (2007)

8. Zhang, W., Shan, S., Gao, W., Chen, X., Zhang, H.: Local gabor

binary pattern histogram sequence (LGBPHS): A novel non-

statistical model for face representation and recognition. In:

Proceedings of the Tenth IEEE International Conference on

Computer Vision (ICCV’05), 786–791 (2005)

9. Gabor, D.: Theory of communication. J. Inst. Elec. Eng. (J-IEE

London) 93(26), 429–457 (1946)

10. Granlund, G.H.: In search of a general picture processing opera-

tor. Comput. Graph. Image Process. (CGIP) 2, 155–173 (1978)

11. Daugman, J.: Uncertainty relation for resolution in space, spatial

frequency and orientation optimized by two-dimensional visual

cortical ﬁlters. J. Opt. Soc. Am. 2(7), 1160–1169 (1985)

12. Ojala, T., Pietika

inen, M., Harwood, D.: A comparative study of

texture measures with classiﬁcation based on feature distribu-

tions. Pattern Recognition 29, 51–59 (1996)

13. Ojala, T., Pietika

inen, M., Ma

enpa

, T.: Multiresolution gray-

scale and rotation invariant texture classiﬁcation with local

binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 24,

971–987 (2002)

14. Daugman, J.: High conﬁdence visual recognition of persons by a

test of statistical independence. IEEE Trans. Pattern Anal. Mach.

Intell. 15(11), 1148–1161 (1993)

15. Lades, M., Vorbru

ggen, J.C., Buhmann, J., Lange, J., von der

Malsburg, C., Wu

rtz, R.P., Konen, W.: Distortion invariant

object recognition in the dynamic link architecture. IEEE

Trans. Comput. 42, 300–311 (1993)

Local Surface Patch

A ‘‘local surface patch’’ (LSP) is deﬁned as the region

consisting of a feature point P and its neighbors N. The

LSP representation includes feature point P, its surface

type, centroid of the patch, and a histogram of shape

index values vs. dot product of the surface normal at

point P and its neighbors. A local surface patch is

shown in Fig. 4. The neighbors satisfy the following

conditions,

N ¼fpixels N; k N  P kЄ

and a cosðn

 n

< AÞ;

ð1Þ

where



denotes the dot product between the surface

normal vectors n

and n

at point P and N and acos

denotes the inverse cosine function. The two para-

meters Є1 and A (Є1 = 5.8 mm, A = 0.5) are important

since they determine the descriptiveness of the local

surface patch representation. A local surface patch is

not computed at every pixel in a range image, but only

at selected feature points. The feature points are de-

ﬁned as the local minimum and the maximum of

shape indexes, which can be calculated from principal

curvatures.

▶ Ear Biometrics, 3D

Localization

▶ Human Detection and Tracking

Localization

949