Малхорта, Нэреш К. Маркетинговые исследования. Практическое руководство

Подождите немного. Документ загружается.

Таблица 19.3. Результаты анализа главных компонент

Критерий сферичности

Бартлетта

Приближенное значение статистики

хи-квадрат-

111,314;

число степеней свободы - 15;

значимость

- 0,00000

Критерий адекватности выборки

Кайэера-Мейера-Олкина

- 0,660

Общности

Переменная Начальная

Выделенная

l/i

1,000

1/5

1,000

1/6

1,000

Исходные

собственные

значения

Фактор

Собственное

значение

2,731

2,218

3 0,442

0,341

0,183

6 0,085

0,926

0,723

0,894

0,739

0,878

0,790

•

Процент дисперсии

45,520

36,969

7,360

5,688

3,044

1,420

Кумулятивный процент

45,520

82,488

89,848

95,536

98,580

100,000

Сумма

квадратов

нагрузок для выделенных факторов

Фактор Собственное значение

2,731

2,218

Матрица факторных нагрузок

Фактор 1

l/i

0,928

1/2

-0,301

1/э

0,936

1/4

- 0,342

1/5

- 0,869

1/6

-0,177

Процент

дисперсии

45,520

36,969

Фактор 2

0,253

0,795

0,131

0,789

-0,351

0,871

Кумулятивный

процент

45,520

82,488

Суммы квадратов факторных нагрузок после вращения факторов

Фактор Собственное значение

1 2,688

2,261

Процент

дисперсии

44,802

37,687

Кумулятивный

процент

44,802

82,488

724

Часть III. Сбор, подготовка и анализ данных

Окончание табл.

19.3

Матрица

факторных

нагрузок после вращения

факторов

Фактор 1 Фактор 2

1/2

1/6

0,962

-0,057

0,934

-0,098

-0,933

0,083

0,027

0,848

-0,146

0,854

-0,084

0,885

Матрица

коэффициентов

значения факторов

Фактор 1 Фактор 2

0,358 0,011

-0,001 0,375

0,345 - 0,043

-0,017 0,377

l/s

- 0,350 - 0,059

0,052 0,395

Вычисленная корреляционная матрица

1/2

1/5

0,926'

0,078

0,902

-0,117

- 0,895

0,057

0,024

0,723'

-0,177

0,730

-0,018

0,746

- 0,029

0,022

0,894*

-0,217

0,859

-0,051

0,031

-0,158

0,031

0,739*

0,020

0,748

0,038

0,081

- 0,027

0,878'

-0,152

- 0,053

-0,105

0,033

-0,107

0,016

0,790*

'Нижний

левый треугольник содержит вычисленную

корреляционную

матрицу;

диагональ

- общности; верхний правый тре-

угольник — остатки между

наблюдаемыми

и вычисленными

корреляциями.

Определение метода факторного анализа

Поскольку установлено, что факторный анализ подходит для анализа данных, необходимо

выбрать соответствующий метод его выполнения. Различные методы факторного анализа раз-

личают в зависимости от подходов, используемых для выделения коэффициентов значения

факторов. Существует два метода — анализ главных компонент и анализ общих факторов. При

анализе главных компонент (principal components analysis) учитывают всю дисперсию данных.

Анализ главных компонент (principal

components

analysis)

Метод

факторного

анализа, который учитывает всю дисперсию данных.

Диагональ

корреляционной

матрицы состоит из единиц, и вся

дисперсия_введена

в матри-

цу факторных нагрузок. Анализ главных компонент рекомендуется выполнять, если основная

задача исследователя — определение минимального числа факторов, которые вносят макси-

мальный вклад в дисперсию данных, чтобы в последующем использовать их в

многомерном

анализе. Эти факторы называют

&швными

компонентами (principal component).

Глава 19. Факторный анализ 725

В анализе

общих

факторов (common factor analysis) факторы определяют только на основа-

нии общей дисперсии. Общности располагаются на диагонали

корреляционной

матрицы.

Этот

метод

подходит,

если основной задачей является определение латентных переменных и общей

дисперсии. Этот метод также известен

какра&южение

матрицы (principal axis factoring).

Анализ

общих факторов (common factor

analysis)

Метод факторного анализа, который

оценивает

факторы только по общей (для всех

факто-

ров) дисперсии.

Существуют и другие методы

оценки

общих факторов. Они включают: метод невзвешенных

наименьших квадратов, обобщенный метод наименьших квадратов, метод максимального

правдоподобия,

ачьфа-

факторны

метод, распознования образов. Эти методы сложнее, и их не

рекомендуется использовать неопытным аналитикам

[8].

В табл. 19.3 показано применение анализа главных компонент. В колонке

"Исходные"

(часть таблицы под названием "Общности") видно, что значения общностей для каждой пере-

менной от

V]_

до

равны 1, поскольку

единицы

введены в диагональ корреляционной матри-

цы. Часть табл. 19.3 под названием

"Исходные

собственные значения" дает собственные значе-

ния факторов, которые снижаются при переходе от первого фактора к шестому. Собственное

значение фактора указывает полную дисперсию, присущую данному фактору. Полная диспер-

сия для всех шести факторов равна 6, т.е. числу переменных. Дисперсия, обусловленная влия-

нием первого фактора, равна 2,731 или 45,52% от полной дисперсии (2,731/6). Аналогично,

дисперсия, обусловленная влиянием второго фактора, равна (2,218/6) или 36,97% от полной

дисперсии, и два фактора вместе объясняют 82,49% полной дисперсии. Для

определения

числа

факторов, которые необходимо использовать в анализе, существует несколько методов.

Определение числа факторов

Можно вычислить столько главных компонент, сколько имеется переменных, но это не-

экономично. Чтобы обобщить информацию,

содержащуюся

в исходных переменных, лучше

выделить небольшое число факторов. Вопрос в том: сколько? Для определения числа факторов

предлагается несколько процедур:

определение,

основанное на предварительной информации;

определение, основанное на собственных значениях факторов; критерий "каменистой осыпи";

определение на основе процента объясненной дисперсии; метод расщепления и критерии

значимости.

Определение, основанное на предварительной информации. Иногда, руководствуясь предва-

рительной информацией, исследователь знает, сколько факторов можно ожидать, и таким об-

разом, может заранее определить число выделяемых факторов. После извлечения желаемого

числа факторов их выделение

прекращают.

Большинство компьютерных программ

позволяют

пользователю определить число факторов, значительно упрошая применение этого метода.

Определение, основанное на собственных значениях факторов. В этом методе учитывают

только факторы, собственные значения которых выше 1,0; остальные факторы в модель не

включают. Собственное значение представляет

значение

дисперсии, обусловленной действием

этого фактора. Следовательно, рассматривают только факторы с дисперсией выше 1,0. Если

число переменных меньше 20, то этот метод завышает число факторов.

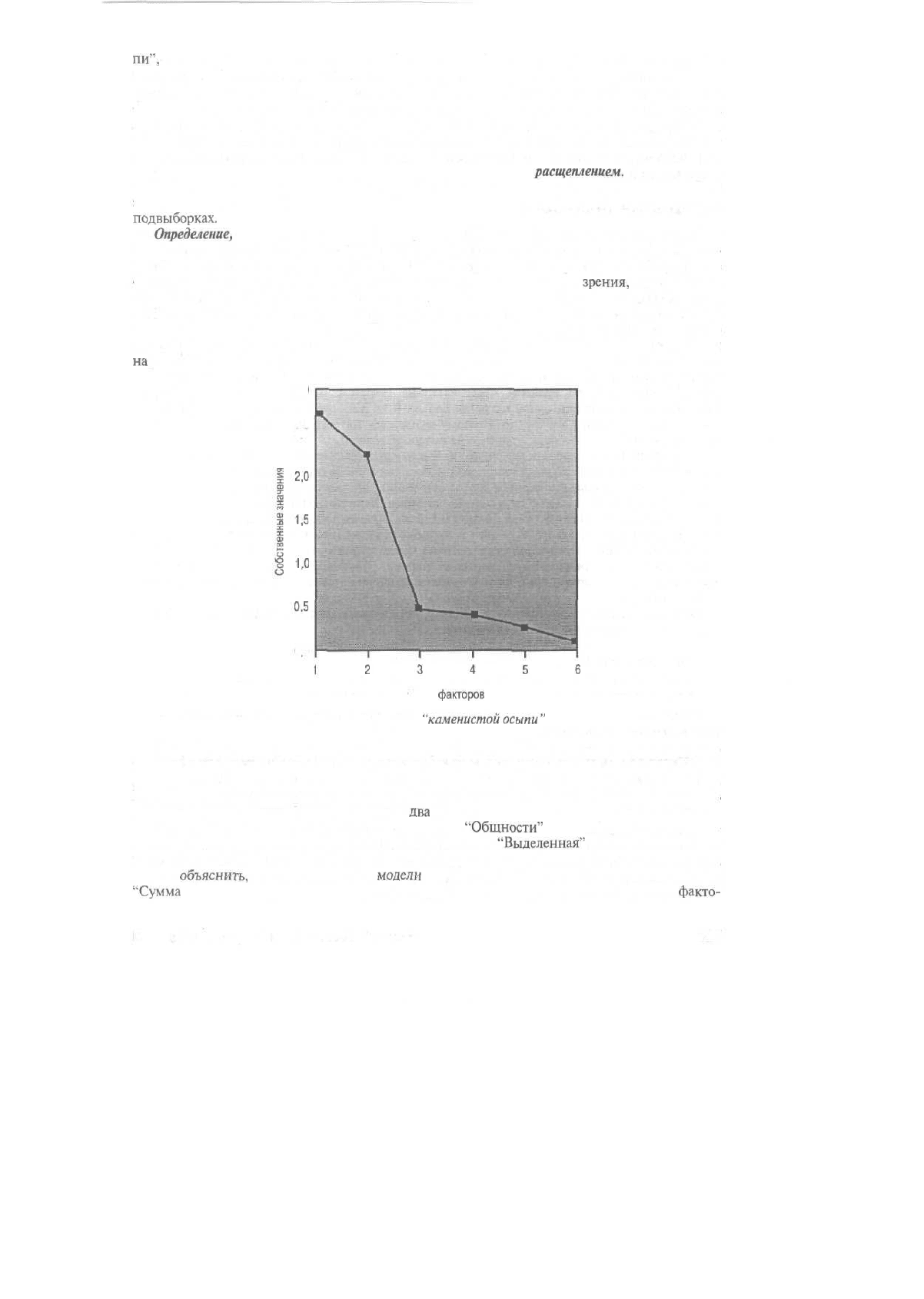
Определение, основанное на критерии

"каменистой

осыпи". Графическое изображение кри-

терия

"каменистой

осыпи" представляет собой график зависимости собственных значений

факторов от их номеров в порядке выделения. Для определения числа факторов используют

форму графика. Обычно график имеет четкий разрыв между крутой частью кривой, где факто-

рам свойственны

большие

собственные значения, и плавной хвостовой частью кривой, связан-

ной с остальными факторами (в этом месте убывание

собственных

значений факторов слева

направо максимально замедляется). Это плавное убывание собственных значений называется

осыпь (scree). Опыт показывает, что точка, с которой

начинается

осыпь, указывает на действи-

тельное число факторов. Обычно число факторов, определенное по графику "каменистой

осы-

726

Часть III. Сбор, подготовка и анализ данных

пи'",

на единицу или несколько единиц больше числа факторов, полученных методом, осно-

ванным на собственных значениях.

Определение на основе процента объясненной дисперсии. В этом методе число выделяемых

факторов определяют так. чтобы кумулятивный процент дисперсии, выделяемой факторами,

достиг удовлетворительного уровня. Какой уровень дисперсии считать удовлетворительным,

зависит от поставленной задачи. Однако рекомендуется выделять такое число факторов, кото-

рое объясняют, по крайней мере, 60% дисперсии.

Определение, основанное на оценке надежности, выполняемой

расщеплением.

В этом методе

выборку расщепляют напополам и факторный анализ выполняют для каждой половины. При

этом оставляют только факторы с высокой степенью соответствия факторных нагрузок в двух

подвыборках.

Определение,

основанное на критериях значимости. Можно определить статистическую зна-

чимость отдельных собственных значений и оставить только статистически значимые факто-

ры. Недостаток этого метода в том, что при больших размерах выборок (больше 200) многие

факторы, вероятно, статистически значимые, хотя с практической точки

зрения,

многие из них

объясняют небольшую долю полной дисперсии.

В табл. 19.3, исходя из собственных значений факторов, превышающих единицу (по умол-

чанию), будет выделено два фактора. Из опыта (предварительная информация) мы знаем, что

зубную пасту покупают по двум основным причинам. График "каменистой осыпи" приведен

на

рис. 19.2.

3.0

2,5

2,0

1.5

1.0

0,5

0.0

23456

Число

факторов

Рис. 19.2, График

"каменистойосыпи"

На графике четкий разрыв виден в области трех факторов. И наконец, из значения кумуля-

тивного процента объясненной дисперсии видно, что два первых фактора объясняют 82,49%

дисперсии, и увеличение этого значения при переходе к трем факторам будет предельным.

Кроме того, метод расщепления выборки также указывает на два фактора. Таким образом, в

данной ситуации целесообразно рассмотреть

два

фактора.

Во второй колонке части табл. 19.3 под названием

"Общности"

дана информация после вы-

деления желаемого числа факторов. Общности в колонке

"Выделенная"

отличаются от значе-

ний в колонке "Начальная", поскольку всю дисперсию, соответствующую этим переменным,

нельзя

объяснить,

если не оставить в

модели

все факторы. В части таблицы под названием

"Сумма

квадратов нагрузок выделенных факторов" даны дисперсии, соответствующие

факто-

Глава 19. Факторный анализ

727

рам, которые оставили в модели. Обратите внимание, что их значения совпадают со значения-

ми дисперсий в колонке "Исходные собственные значения". Это характерно для анализа глав-

ных компонент. Процент дисперсии, объясненной фактором, определяют, разделив соответст-

вующее

собственное значение на число факторов и умножив полученное значение на 100. Та-

ким образом, первый фактор объясняет (2,731/6) х 100, или 45,52%, от дисперсии,

соответствующей шести переменным. Аналогично, второй фактор объясняет (2,218/6) х 100,

или 36,969% полной дисперсии. Интерпретация решения часто становится более ясной после

вращения факторов.

Вращение факторов

Важный результат факторного

анализа—

матрица факторных нагрузок, также называемая

матрицей факторного отображения (factor pattern matrix). Она содержит коэффициенты, ис-

пользуемые для выражения нормированных переменных через факторы. Эти коэффициенты,

называемые факторными нагрузками, представляют корреляции между факторами и перемен-

ными. Коэффициент с высоким абсолютным значением показывает, что фактор и переменная

тесно взаимосвязаны. Коэффициенты матрицы факторных нагрузок можно использовать для

интерпретации факторов.

Несмотря на то, что

матрица

исходных или неповернутых факторов указывает на взаимо-

связь факторов и отдельных переменных, она редко приводит к факторам, которые можно ин-

терпретировать,

поскольку факторы коррелируют со многими переменными. Например, в

табл. 19.3 фактор 1, по крайней мере, частично связан с пятью из шести переменных

(абсолютное значение факторной нагрузки больше 0,3). Как интерпретировать этот фактор? В

такой сложной матрице это трудно. Поэтому вращением матрицу факторных коэффициентов

преобразуют

более простую, которую легче интерпретировать.

При

вращении

факторов желательно, чтобы каждый фактор имел ненулевые или значи-

мые нагрузки (коэффициенты) только для небольшого числа переменных. Аналогично, же-

лательно, чтобы каждая переменная имела ненулевые или значимые нагрузки с небольшим

числом фактором, если можно, то с одним фактором. Если несколько факторов имеют высо-

кие значения факторных нагрузок с одной и той же переменной, то их трудно интерпретиро-

вать. Вращение не влияет на общности и процент объясненной полной дисперсии. Однако

процент дисперсии, обусловленной влиянием каждого фактора, изменяется. Это видно из

данных табл. 19.3. В результате вращения дисперсия, объясняемая каждым фактором, пере-

распределилась. Следовательно, разные методы вращения помогают интерпретировать раз-

личные факторы.

Вращение

называют ортогональным

вращением

(orthogonal rotation), если при вращении со-

храняется прямоугольная система координат.

Ортогональное вращение (orthogonal rotation)

Вращение факторов, при котором

сохраняется

прямоугольная

система координат.

Самый распространенный метод вращения — метод

варимакс

(вращение, максимизирующее

дисперсию)

(varimax

procedure).

Метод

варимакс,

или

вращение,

максимизирующее

дисперсию)

(varimax procedure)

Ортогональный метод вращения

факторов,

который минимизирует число переменных с вы-

сокими значениями нагрузок,

усиливая

тем

самым

интерпретируемость

факторов.

Это ортогональный метод вращения, который минимизирует число переменных с высоки-

ми значениями нагрузок, усиливая тем самым интерпретируемость факторов [9]. В результате

ортогонального вращения получают некоррелированные факторы. Вращение называют косо-

угольным вращением (oblique rotation), если

не

сохраняется прямоугльная система координат и в

результате

вращения

получают коррелированные факторы.

728 Часть III. Сбор, подготовка и анализ данных

Косоугольное вращение (oblique rotation)

Вращение факторов, при котором не

сохраняется

прямоугольная

система координат.

Иногда, допустив некоторую

корреляцию

между факторами, можно упростить матрицу

факторной модели. Косоугольное вращение

используется

тогда, когда факторы в генеральной

совокупности, вероятно, тесно взаимосвязаны.

Сравнив в табл. 19.3 матрицу

факторных

нагрузок, полученную после применения метода

врашения

варимакс, с матрицей факторных нагрузок до вращения (часть таблицы под назва-

нием "Матрица факторных нагрузок"), мы увидим, как

вращение

упрощает и усиливает ин-

терпретируемость факторов. В то время как в неповернутой матрице пять переменных коррели-

руют с фактором I, после вращения с фактором 1 коррелируют только переменные

Остальные переменные

коррелируют с фактором 2. Более того, ни одна из перемен-

ных не коррелирует достаточно сильно с обоими факторами. Повернутая матрица создает осно-

ву для интерпретации факторов.

Интерпретация факторов

Для интерпретации факторов необходимо определить переменные, которые имеют высокие

значения нагрузок по одному и тому же фактору. А затем этот фактор следует проанализировать

с учетом этих переменных. Другое полезное средство интерпретации — графическое изображе-

ние переменных, координатами которых служат величины факторных нагрузок. Так, в конце

оси расположены переменные, которые имеют большие нагрузки только в связи с этим факто-

ром и, следовательно, характеризуют его. Переменные в начале координат имеют небольшие

нагрузки в связи с обоими факторами. Переменные, расположенные вдали от осей, связаны с

обоими факторами. Если фактор нельзя четко определить с точки зрения связи с исходными

переменными, то его следует пометить как неопределяемый или генеральный (общий для всех

переменных).

-0,5'

-1.0

-0,5

0,0 0,5 1

Фам

op 1

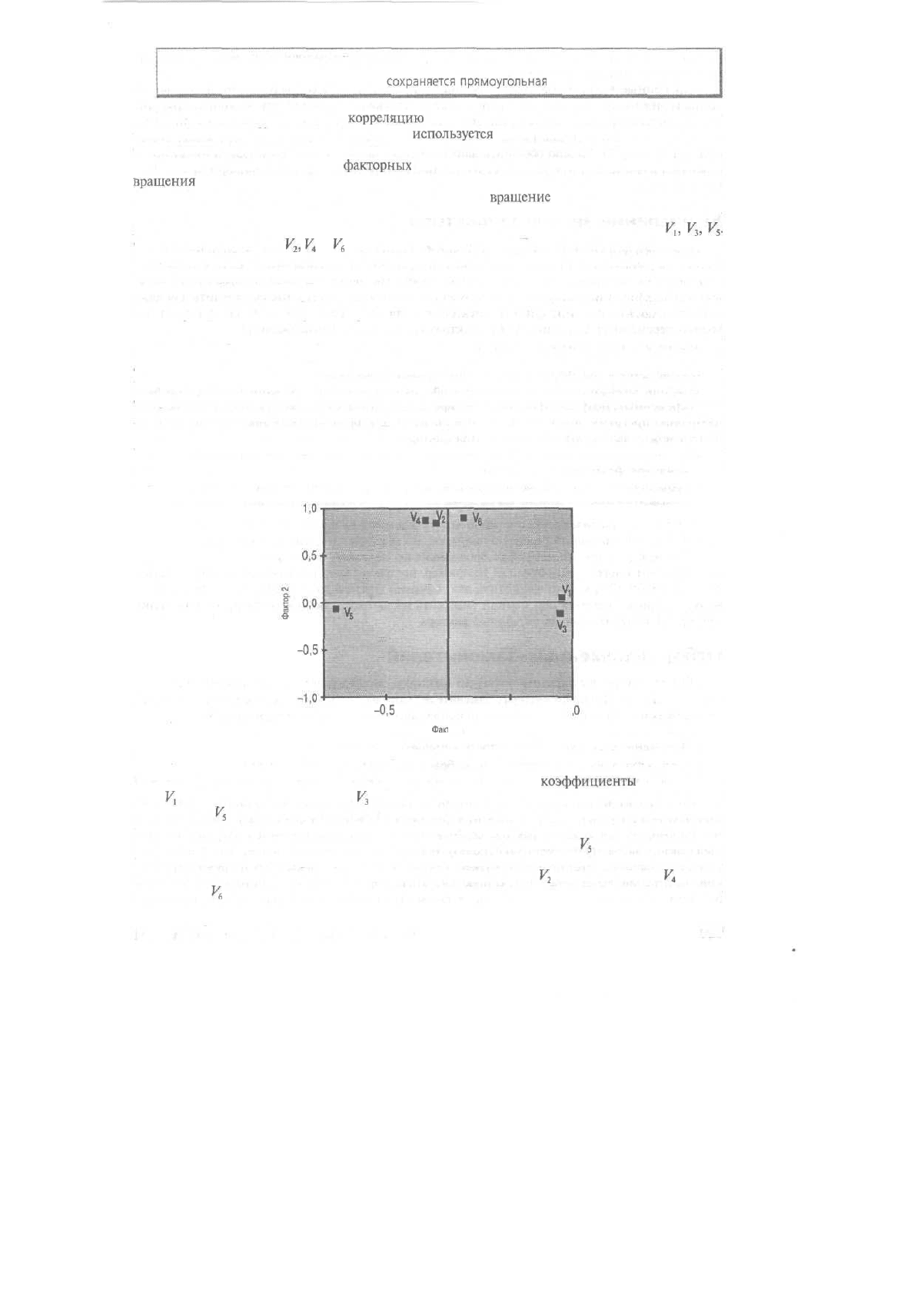
Рис, 19.3. Диаграмма факторных нагрузок

В повернутой матрице из табл. 19.3 фактор 1 имеет высокие

коэффициенты

для перемен-

ных

Г,

(предотвращение кариеса),

К,

(укрепление десен), и отрицательный коэффициент для

переменной

(предотвращение порчи зубов не считается важным при покупке зубной пасты).

Следовательно, этот фактор можно назвать фактором, укрепляющим здоровье. Обратите вни-

мание, что отрицательный коэффициент для негативной переменной

ведет к положитель-

ной интерпретации этого фактора, а именно, предотвращение порчи зубов будет важным при

покупке зубной пасты. Фактор 2 тесно связан с переменными

(белизна зубов),

(свежее

дыхание) и

(привлекательность внешнего вида зубов). Таким образом, фактор 2 можно по-

Глава 19. Факторный анализ

729

метить как фактор,

отвечающий

за внешний вид. Диаграмма факторных нагрузок на рис.

19.3

подтверждает эту интерпретацию факторов.

Переменные

FJ,

(обозначенные на диаграмме 1, 3 и 5 соответственно) находятся на

конце горизонтальной оси, причем точка, соответствующая

находится на конце, противо-

положном месту расположения точек, соответствующих

{

В то же время переменные

(обозначенные на диаграмме 2, 4 и 6 соответственно) расположены на конце вертикаль-

ной оси (фактор 2). Можно

обобщить

данные, сделав вывод, что потребители, по-видимому,

стремятся извлечь двойную пользу из зубной пасты: укрепить здоровье и приобрести хороший

внешний вид.

Вычисление значения фактора

После интерпретации факторов необходимо вычислить их значения. Факторный анализ

имеет собственную ценность. Однако если цель факторного анализа заключается в снижении

исходного числа переменных до небольшого набора составных переменных (факторов), кото-

рые в дальнейшем используются в многомерном

анализе,

то имеет смысл вычислить для каж-

дого респондента значение фактора. Фактор представляет собой линейную комбинацию ис-

ходных переменных. Значение для

/-го

фактора можно вычислить по формуле

Обозначения в этой формуле аналогичны приведенным выше.

Веса или коэффициенты значения фактора, используемые для объединения нормирован-

ных переменных, получают из матрицы коэффициентов значения фактора. Большинство ком-

пьютерных программ позволяет вычислить значения факторов. Только в анализе главных ком-

понент можно вычислить точные значения факторов.

Значение фактора (factor

scores)

Суммарное значение, полученное для каждого респондента на основании всех факторов.

Более того, в анализе главных компонент эти значения не взаимосвязаны. В анализе общих

факторов оценки значений факторов получают, но нет гарантии, что факторы не будут корре-

лировать между собой. Значения факторов можно использовать вместо исходных переменных в

последующем многомерном анализе. Например, используя матрицу коэффициентов значения

фактора в табл. 19.3, можно

вычислить

два значения фактора для каждого респондента. Если

нормированные значения переменной умножить на соответствующий коэффициент значения

фактора, то получится значение данного фактора.

Отбор переменных-заменителей

Иногда, вместо вычисления значений факторов, исследователь может выбрать перемен-

ные-заменители. Выбор переменных-заменителей (surrogate variables), заключается в выделении

нескольких из исходных переменных для использования их в последующем анализе,

Переменные-заменители

(surrogate

variables)

Часть набора исходных переменных,

выбранных

для последующего анализа.

Это позволит выполнить

последующий

анализ и интерпретировать результаты с точки зре-

ния исходных переменных, а не значения

факторов.

Из матрицы факторных коэффициентов

можно выбрать для каждого фактора переменную с наивысшим значением нагрузки на дан-

ный фактор. Затем эту переменную используют в качестве

перемен

ной-заменителя

для соответ-

ствующего фактора. Этот процесс протекает гладко, если одна из факторных нагрузок перемен-

ной значительно выше остальных. Однако сделать выбор не так легко, если нагрузки двух или

больше переменных одинаково высокие. В таком случае выбор осуществляют, исходя из теоре-

730 Часть

III.

Сбор, подготовка и анализ данных

тических предпосылок. Например, теоретически предполагают, что переменная с несколько

меньшей нагрузкой важнее, чем переменная с несколько большей нагрузкой. Аналогично, если

переменная имеет несколько меньшую, но более точно измеренную нагрузку, то в качестве пе-

ременной-имитатора следует выбрать именно ее. В табл. 19.3 переменные

}

имеют вы-

сокие нагрузки в связи с фактором 1, причем достаточно близкие по величине. Переменная

имеет относительно самое высокое значение и поэтому должна была бы оказаться вероятным

кандидатом в переменные-имитаторы. Однако, исходя из предварительной

информации,

са-

мым важным при выборе зубной пасты является ее способность

предотвращать

порчу зубов, и

поэтому в качестве переменной-заменителя для фактора 1 должна быть выбрана переменная

Осуществить выбор переменной-заменителя для фактора 2 также непросто. Переменные

К,

имеют сопоставимо высокие значения нагрузок на этот фактор. Если предварительная ин-

формация свидетельствует, что привлекательность внешнего вида зубов — важнейший аспект

общего

внешнего вида, то следует выбрать переменную

Определение подгонки модели

Последняя стадия факторного анализа заключается в определении соответствия модели

факторного анализа исходным данным, т.е. степени ее подгонки. Основное допущение, лежа-

щее в основе факторного анализа, состоит в том, что наблюдаемая корреляция между перемен-

ными может быть свойственна общим факторам. Следовательно, корреляции между перемен-

ными можно вывести или воспроизвести из определенных корреляций между переменными и

факторами. Изучив разности между наблюдаемыми корреляциями (данными в исходной кор-

реляционной матрице) и вычисленными корреляциями (определенными из матрицы фактор-

ных нагрузок), можно определить соответствие модели исходным данным. Эти разности назы-

вают остатками (residuals). Если много остатков с большими значениями, то факторная модель

не обеспечивает хорошее соответствие данным и требует пересмотра. Из данных табл. 19.3 вид-

но, что только значение пяти остатков превышает 0,05, свидетельствуя тем самым о приемле-

мом соответствии модели данным.

Следующий пример иллюстрирует анализ главных компонент с точки зрения продвижения

товара.

ПРИМЕР. Компоненты, влияющие на продвижение на рынок промышленных

товаров

Цель этого исследования — определить достаточно большой набор контролируемых

производителем переменных, имеющих отношение к продвижению его товаров в рознич-

ную торговую сеть, и показать, что существует связь между этими переменными и реше-

нием розничного торговца о поддержке усилий производителя по продвижению товара.

Решения о поддержке определяли по отношению розничного торговца к усилиям по про-

движению товара.

Факторный анализ выполнили по объясняющим переменным, руководствуясь главной

целью — снизить количество переменных. Методом главных компонент с использованием

метода вращения варимакс уменьшили 30 объясняющих переменных до 8 факторов с собст-

венными значениями выше 1,0. Для интерпретации каждый фактор включал в себя пере-

менные с нагрузками на этот фактор от 0,40 и выше. В двух случаях, когда переменные име-

ли нагрузки 0,40 и выше на два фактора, каждой переменной присвоили один фактор, на-

грузка на который была выше. Только одна переменная "легкость

погрузочно-раэгрузочных

работ, накопление запасов в торговых точках" не имела нагрузки, по крайней мере, равной

0,4, ни на один из факторов. В целом, 8 факторов объясняли 62% суммарной дисперсии.

Интерпретация матрицы факторных нагрузок оказалась несложной. В табл. 1 перечислены

факторы в порядке их выделения.

Глава 19. Факторный анализ 731

Таблица 1.

Факторы,

влияющие на принятие решения о поддержке в продвижении товара

фактор

Интерпретация

фактора Нагрузка

Переменные,

включенные

в фактор

(объясненный процент

дисперсии)

Важность

товара (16,3%)

Эластичность продвижения товара на

рынок

(9,3%)

Поддержка торговой марки

произво-

дителем (8,2%)

Репутация производителя (7,3%)

0,В5

0,81

0,80

0,75

О 72

0,72

0,64

0,55

0,51

0,93

093

-0,81

0,69

0,46

0,79

0,72

0,49

0,83

0,81

0,49

Приводится по объективным показателям.

Истощение продвижения товара

(6,4%)

Оборачиваемость продаж (5,4%)

Рентабельность

товара (4,5%)

Сумма

поощрения

(4,2%)

0,77 Товар достаточно важен

для

того, чтобы гарантировать

его продвижение

0,75 Данная категория товара хорошо реагирует на

рекламу

0,66

Вероятно,

наиболее близкий конкурент

занимается

про-

движением данного

товара

0,64 Значимость продвигаемой категории товара

0,59 Товар имеет

постоянный

объем продаж

0,57 Сделка соответствует требованиям обеспечения продви-

жения товара

Оценка покупателями

увеличения

объема продаж основа-

на на

следующем:

0,86

Снижение цены и демонстрация товара

0,82 Только демонстрация товара

0,80

Только снижение цены

0,70 Снижение цены, демонстрация, рекламная кампания

Поддержка торговой марки

производителем

в форме:

Купонов

Радио- и телевизионной рекламы

Рекламы в газетах

Содействие продвижению товара в местах его продажи

(например,

выставки)

Общая репутация производителя

Производитель идет навстречу пожеланиям торговли

Производитель сотрудничает с продавцом в случае экс-

тренных заказах, встречного пробега и

т.д.

Качество представления продаж

Суммарное качество товара

производителя

Чрезмерное продвижение категории

Избыток конкретного товара

Ранг доли рынка торговой

марки

Постоянный объем продаж (данного)

товара

Постоянный объем продаж (данного) товара

Постоянная валовая прибыль (от продажи) товара

Постоянная валовая прибыль

(от

продажи)

товара

Разумность требований по выполнению соглашения

Абсолютная сумма скидок по соглашениям

Скидки по соглашениям как процент регулярной торговой

стоимости(цены)

Абсолютная сумма скидок по

соглашениям

732

Часть III. Сбор, подготовка и анализ данных

Для того чтобы определить, какой из восьми факторов (если такой фактор существует)

предсказывает содействие продвижению товара на рынок в статистически значимой степе-

ни, выполнен пошаговый

дискриминантный

анализ. Значения всех восьми факторов вы-

ступают

объясняющими

переменными. Зависимая переменная состоит из

оценки

(рейтинга) розничным торговцем деловых отношений с производителем, которую разбива-

ют на три группы, в зависимости от степени содействия в продвижении товара

(низкая,

средняя, высокая). Результаты дискриминантного анализа приведены в табл. 2.

Таблица 2. Результаты дискриминантного анализа: анализ по рейтингу

и эффективности

(п

= 564)

Нормированные коэффициенты

дискриминантной

функции

Фактор Функция 1 Функция Z

F\ Важность товара 0,861 - 0,253

Эластичность продвижения товара на рынок 0,081 0,398

Поддержка торговой

марки

производителем 0,127

-0,036

Репутация производителя 0,394 0,014

Истощение

продвижения

товара - 0,207 0,380

Оборачиваемость продаж 0,033 - 0,665

Рентабельность

товара 0,614 0,357

Сумма поощрения 0,461 0,254

Коэффициент

А,

(для каждого фактора) — все

значимы

при р < 0,001

Значения

F-статистик для многомерной выборки — все значимы при р < 0,001

Процент правильно классифицированных случаев — 65% (t = 14,4; р <

0,001)

Все восемь факторов присутствуют в

дискриминантных

функциях. Критерии согласия

указали

на

то, что все восемь факторов дискриминировали (различали) высокий, средний и

низкий уровни содействия продажи

товара,

.^-статистики

для многомерной выборки,

ука-

зываюшие

на степень дискриминации между каждой парой групп, были значимыми при р

0,001.

65% случаев было верно отнесено к высокому, среднему и низкому уровню содейст-

вия продвижению товаров. Использовался порядок введения в дискриминантный анализ.

I Для того чтобы определить относительную важность факторов, влияющих на содействие

торговле, факторы в

дискриминантную

функцию вводили в порядке, указанном в

j табл. 3 [10],

Таблица 3.

Относительная

важность факторов, влияющих на содействие торговле

i (показано с помощью порядка ввода в дискриминантный анализ)

Анализ

рейтинга

I Порядок ввода Название фактора

1 Важность товара

2 Эластичность продвижения

товара

на рынок

3 Поддержка торговой марки производителем

4 Репутация производителя

Истощение

продвижения

товара

о Оборачиваемость продаж

7 Рентабельность товара

Сумма

поощрения

В следующем разделе описан анализ общих факторов с примерами применения этого метода.

Глава 19.

Факторный

анализ 733