Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

342 IIIb. Fluid Mechanics: Incompressible Viscous Flow

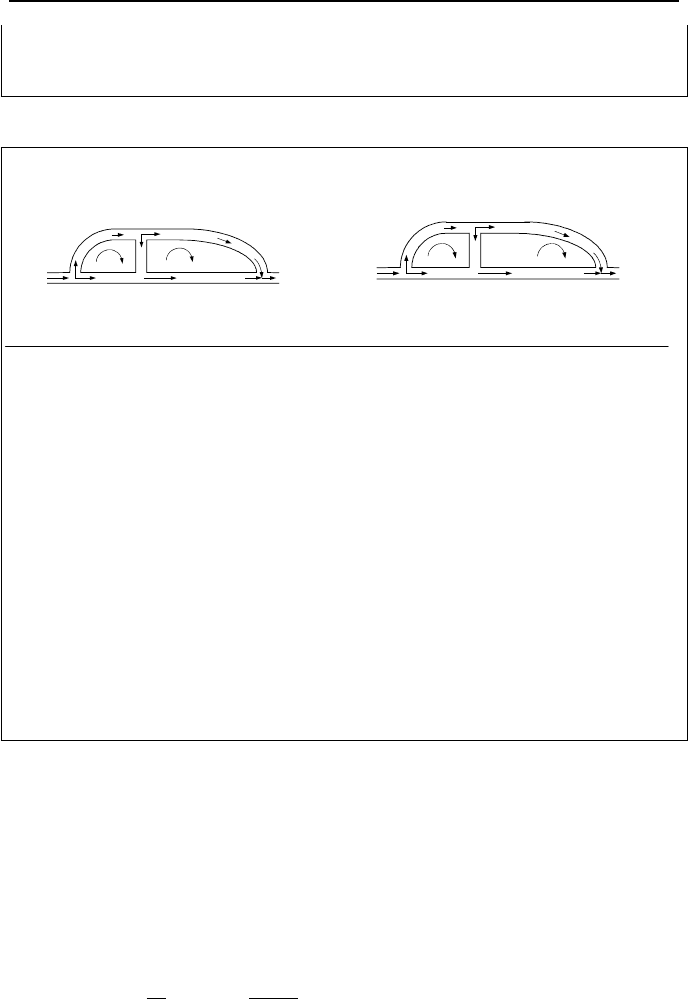
Final results are shown in the right side figure. Although, we could have made

better initial guesses such as (c = 6, 5), (c = 10, 60), (c = 12, 40), (c = 2, 15), and

(c = 4, 35), the number of trials would still be 3.

Example IIIb.5.2. Find flow distribution in the left side network for the given

data. Use n = 2.

1 lit/s

1 m

1 lit/s

0.448 lit/s

0.552 lit/s 0.613 lit/s

0.387 lit/s

0.061 lit/s

Pipe L (m) D (m) A (m

) f c (from Equation IIIb.3.7)

1 507.6 0.55 0.237 0.012 10

2 143.7 0.40 0.126 0.013 15

3 47.9 0.40 0.126 0.013 5

4 628 0.50 0.196 0.012 20

5 114 0.30 0.071 0.013 50

Solution: We assume the clockwise direction as positive for each loop and use an

initial guess for the flow in each loop to be corrected in the following steps. Using

the procedure of Example IIIb.5.1, we obtain:

Trial



∆

0 –0.60 0.40 –0.100 –0.500 0.500 0.0 0.0

1 –0.55 0.45 0.565 –0.60556 0.3934 0.05 0.10656

2 –0.5511 0.4488 0.06113 –0.6123 0.3877 –0.00114 –0.00571

3 –0.5513 0.44873 0.06101 –0.61228 0.38772 –0.00013 –0.00001

4 –0.55127 0.44873 0.06101 –0.61228 0.38772 0.00000 0.00000

The results are shown in the right side figure.

The Carnahan Method

In this method, we express flow rates in terms of pressure difference between the

adjacent nodes. The summation of all the flow rates at each node, according to

Equation IIIb.5.1 must be zero. Hence, we obtain as many equations as the num-

ber of nodes. To elaborate, let’s consider two adjacent nodes, i and j, the momen-

tum equation for the flow path connecting these nodes is given by Equa-

tion IIIb.4.1:

()

0)(

)K(

=−+++−

ijij

ZZg

fPP



6. Unsteady Internal Incompressible Flow 343

where we assumed that there is no pump in flow path ij. Treating friction factor as

a constant and considering the special case of flow distribution in the horizontal

plane, this equation becomes:

ijji

jiij

cPP

PPm

−

−=

)(



IIIb.5.7

where in Equation IIIb.5.7,

)2/()K/(

ADfLc

ijij

+= . Per Carnahan, the

advantage of factoring out the nodal pressure difference in Equation IIIb.5.7 is that

the square root would always have a real value. Additionally, if pressure of node i

is higher than that of node j, then flow would leave node i with a plus sign. Oth-

erwise, flow would enter node i, with a minus sign as it should. Similar equations

can be written for other flow paths connected to j. The summation of all the flow

rates for node j must be equal to zero:

)(

−

−=

¦¦

ijji

cPP

PPm



Where n represents total number of flow paths connected to node j. Similar equa-

tions can be written for the rest of the nodes, resulting in a set of non-linear alge-

braic equations. Such set can be solved by the Newton-Raphson iteration method

as discussed in Chapter VII or by the successive-substitution method. In the latter

method, P

is calculated from:

−

¦¦

ijji

cPPcPP

Similar relations can be obtained for all other nodes. An initial guess is made for

all the nodes. These initial guesses are then used in the right side of the above

equations to update the guesses. The process continues until the difference in suc-

cessive guesses becomes exceedingly small. The process is converged when the

absolute value of the pressure difference divided by the updated pressure becomes

smaller than a specified convergence criterion. Having calculated nodal pressures,

inter-nodal flow rates can then be determined. Care must be exercised when flow

encounters valves and fittings that induce large pressure drops. In such cases, the

local pressure may drop below the vapor pressure corresponding to the liquid tem-

perature, which may lead to cavitation as discussed in Chapter VI.

6. Unsteady Internal Incompressible Flow

In this section we analyze the unsteady, internal, one-dimensional flow of a single-

phase incompressible fluid in single-path systems and flow distribution in multi-

344 IIIb. Fluid Mechanics: Incompressible Viscous Flow

path systems. Transient or unsteady fluid flow is due to the departure from steady

state and stagnation conditions. Changing the flow area, such as throttling of a

regulating valve or the speed of an operating pump would induce flow transients.

Other examples of flow transients include pipe ruptures, loss of power to pumps,

and actuation of safety and relief valves. Flow transients can be divided into two

categories. The first category includes slow transients also referred to as rigid

column theory. In these types of transients, the assumption is that the entire body

of fluid moves as a rigid body. Also the liquid is assumed to be incompressible

and the conduit carrying the liquid fully rigid. Hence, any disturbance in the me-

dium is propagated instantly throughout the system.

The second category includes fast transients when there is a rapid change in

flow velocity or fluid density. Analysis of fast transients is more complicated than

the analysis of slow transients. This is because the compressibility of the fluid and

the elasticity of the conduit containing the fluid must be accounted for. Although

in many applications liquids may be treated as incompressible, in reality even liq-

uids possess some degree of compressibility. Mathematically, problems involving

slow transients can be solved with ordinary differential equations while the analy-

sis of fast transients includes solution to partial differential equations as pressure,

),( trP

and velocity, ),( trV

are in general functions of both space and time. This

type of transient is known as waterhammer or elastic analysis.

In discussing slow transients, we study such topics as transients in flow loops,

time to fill drained pipelines, and time to empty vessels. We start with simpler ex-

amples of unsteady flow involving the application of the momentum equation.

We then analyze waterhammer in the fast transient category. Employing Equation

IIIa.3.38, we study two types of slow transients. The first type includes problems

for which we may ignore the viscous effects of the incompressible fluid. The sec-

ond type includes the unsteady flow of incompressible viscous flow. We start

with the unsteady flow of incompressible inviscid fluids.

6.1. Unsteady Flow of Internal Incompressible Inviscid Flow

We apply Equation IIIa.3.39 for incompressible inviscid flow along the stream-

lines to a few examples, assuming the working fluid can be treated as an ideal

fluid.

Time To Reach Steady-State Flow Rate

Consider a large reservoir discharging water through a small hole, as shown in

Figure IIIb.6.1(a). In this case, the first term of Equation IIIa.3.39 is negligible

hence we may use the Bernoulli equation at steady-state condition between

points 1 and 2. Noticing that in a large reservoir, water velocity is zero everywhere

except at the hole, we get (See Example IIIa.3.16)

ostate-steady2

h2)( gV =

Therefore the mass flow rate is calculated as:

6. Unsteady Internal Incompressible Flow 345

)4/(h2

o-statesteady

dgm

πρ



We now consider another case where the same tank is connected to a pipe of

length L and the same diameter d as shown in Figure IIIb.6.1(b). Initially, a fast

acting gate valve with zero resistance is fully closed. At time zero the valve is

fully opened. We want to find the time it takes for the water velocity to reach

from zero to its steady-state value.

(a) (b)

Figure IIIb.6.1. Flow of liquid from a large reservoir with fixed height

Since P

= P

and V

= 0, Equation IIIa.3.39 for this case is simplified to:

()

=−++

⋅

∂

ZZg

To integrate the first term along the streamline from point 1 to 2, we note that:

Ldl

≈

⋅

∂

Substituting we obtain,

=−+ g

L IIIb.6.1

Although this is a non-linear differential equation, we can find an analytical solu-

tion by the method of separation of variables, which results in

)2/(2/

VghdVLdt −= . We now integrate this equation between time t = 0

when velocity is V

= 0 to an arbitrary time t to find V

(t):

−

)

(tanh

−

resulting in:

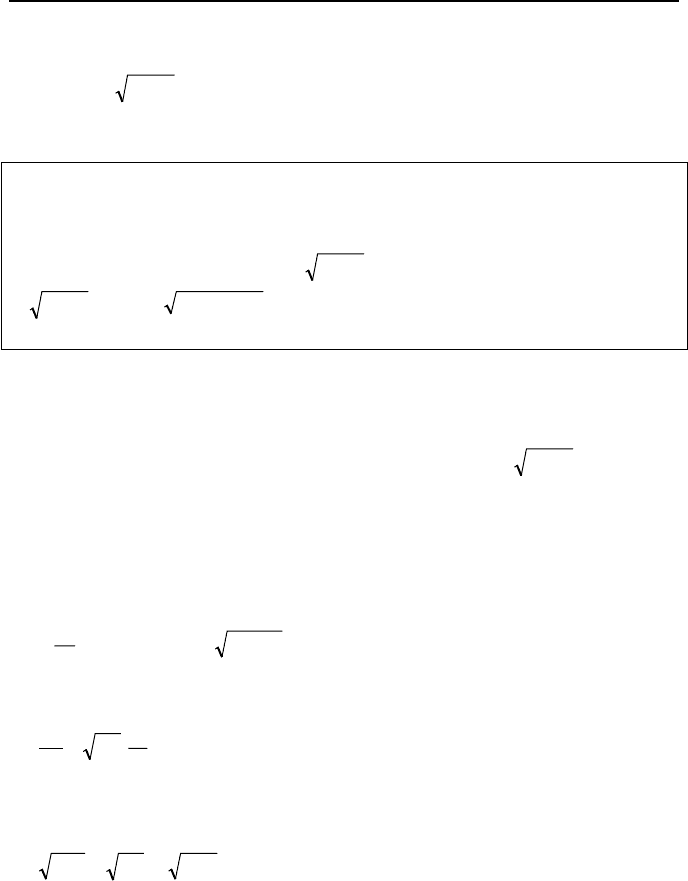
346 IIIb. Fluid Mechanics: Incompressible Viscous Flow

)2/tanh(/

oo2

LtVVV = IIIb.6.2

where

h2gV = . Time for velocity to reach its steady-state value is found

from

1)2/tanh(

=LtV .

Example IIIb.6.1. The initially closed valve in Figure IIIb.6.1(b) suddenly opens.

Find the time it takes for the velocity to reach 50% of its steady-state value. Data:

L = 6 m, h

= 3 m, d = 15 cm.

Solution: We find t from 5.0)2/h2tanh(

=Lgt . The argument becomes

ttLgt 64.0)12/381.92()2/h2(

=××= . Hence, for tanh(0.64t) = 0.5 by it-

eration we find t ≅ 0.87 s.

Static Head as a Function of Time

Liquid is flowing through a small hole in the bottom of a reservoir having a di-

ameter of D, as shown in Figure IIIb.6.1(a). In obtaining

h2gV = , we consid-

ered the reservoir to be large enough so that the available head for flow through

the pipe remains constant. However, if the available head is decreasing as more

flow leaves the tank, then the variation of h = f(t) should be considered. To see

how h is changing versus time, we write the continuity equation for the tank;

d/dt(m

tank

) = –



. Substituting yields:

)(h2)(h

tgaaVt

A −=−=

where d is the diameter of the pipe. From this relation we obtain,

0h)(2

2/12

IIIb.6.3

This is a non-linear differential equation that can be solved by separation of vari-

ables to obtain:

tAagt

)]/(2/[h)(h −=

In the case of the reservoir connected to a pipe with static head decreasing as a

function of time, we must solve Equations IIIb.6.1 and IIIb.6.3 simultaneously, as

discussed in Section IIIb.6.2.

Flow Oscillation in a U-Tube

Another example of unsteady flow is the oscillation of inviscid liquid in a U-tube.

At time zero, we push point 1 causing point 2 to reach the height H (Fig-

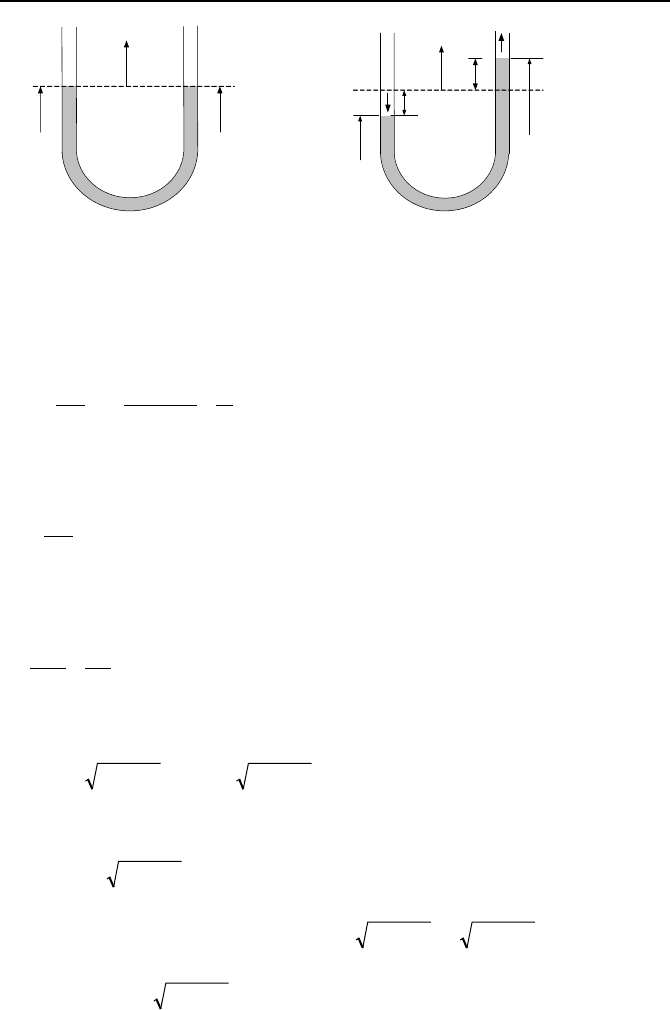
6. Unsteady Internal Incompressible Flow 347

(0)

-H

Figure IIIb.6.2. Flow oscillation of an inviscid fluid in a U-tube

ure IIIb.6.2). We then let go so that the oscillation can begin. Since streamlines

are well defined in this problem and fluid is inviscid, we can apply Equa-

tion IIIa.3.38:

0)()(

1212

=−+−+

−

∂

ZZgPP

where Z

and Z

are measured from an arbitrary datum. Since during the oscilla-

tion P

= P

and V

= V

, Equation IIIa.3.39 reduces to:

0)(

=−+ ZZg

where in this equation, L is the length of the liquid column. Substituting for V =

dz/dt, we get:

=+ z

where z is measured from the line connecting points 1 and 2 at time zero. The so-

lution to this second order, linear differential equation is given as:

tLgctLgcz )/2(sin)/2(cos

+= . Using initial conditions, at t = 0, dz/dt =

0 gives c

= 0. Also at t = 0, z = H hence, c

= H. Therefore, the liquid level at

any given time can be found from:

tLgz )/2(cosH=

Velocity of the column of liquid versus time can be obtained by differentiating

with respect to t, V = dz/dt so that;

tLgLgV )/2(sin)/2(H=

. This deriva-

tion shows that for inviscid liquids, the column has a simple harmonic motion with

a period of T = 2

)2/( gL

348 IIIb. Fluid Mechanics: Incompressible Viscous Flow

atm

P(t), V(t)

, V

Air Control

Volume

Water Control

Volume

time

Figure IIIb.6.3. Draining of a fully insulated tank in a quasi-steady process

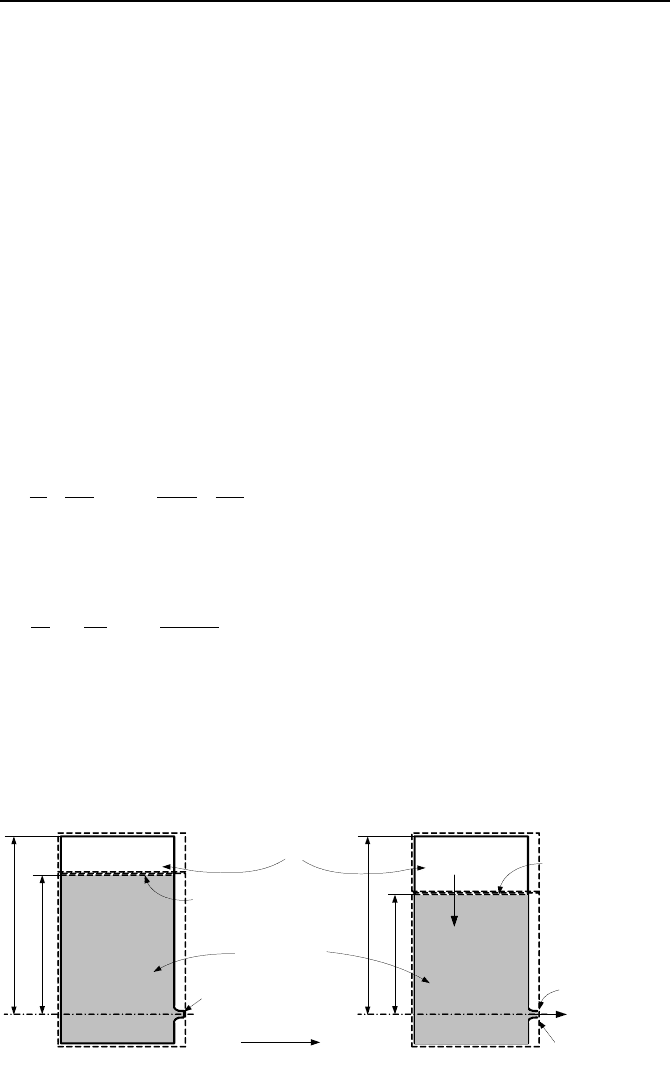
Draining Tanks in a Quasi-steady Process

This is a useful method for cases in which the fluid acceleration in Equa-

tion IIIa.3.39 is so small, in comparison with the other terms, that we can ap-

proximately ignore the time derivative term. Hence, the process is referred to as

quasi-steady. To elaborate let’s try the tank in Figure IIIb.6.1(a), which is now

shown in Figure IIIb.6.3. In this tank, water is covered by a blanket of pressurized

air, initially at P

having a volume of V

. The tank cross sectional area is A

and

the initial water level from the drain centerline is h

. In Figure IIIb.6.3, H is the

fixed elevation of the tank from the drain centerline. The drain flow area is A

. At time zero, we remove the plug and let water drain from the tank. Since the

ratio of A

is very small, we ignore the initial acceleration and assume that the

tank is being drained in a quasi-steady manner. The quasi-steady assumption also

lets us assume reversible expansion of the air region. We may treat the gas expan-

sion as an isentropic process if the tank is fully insulated. This is to prevent any

heat transfer to the expanding air from the surroundings.

In Figure IIIb.6.3, we have identified two control volumes, one for the expand-

ing air region and another for the shrinking water region. We apply Equa-

tion IIIa.3.33, the Bernoulli equation to the water region:

eatmt

++=++

ρρ

where V

= V

, V

= –dh/dt, and Z – Z

= h(t) and . For the gas region, we use

Equation IIa.4.3:

VHh

γγ

−

§·§ ·

¨¸¨ ¸

−

©¹© ¹

We substitute for V

, V

, and P in terms of the known values of H, h

, A

, a and the

only unknown, dh/dt in the Bernoulli equation to obtain:

6. Unsteady Internal Incompressible Flow 349

()

2h/1

iatmt

dt a

ρρ

§·

¨¸

©¹

−

=− − + −

−



To plot h = f(t), we should solve the above first order non-linear differential equa-

tion numerically.

Example IIIb.6.2. Find the time to drain the water tank of Example IIIa.3.16.

Data: h

= 10 ft, a/A

= 0.01.

Solution: We note that V

a = V

= –A

dh/dt. Substituting into V

= (2gh)

1/2

, we

find:

1/ 2

§·

=−

¨¸

©¹

Although a non-linear, differential equation, due to its simplicity we can find the

following analytical solution:

hh 2

§·

=−

¨¸

©¹

Substituting, we find time for h = 0 as

7901.0/2.32/102)//(/h2

=×==

= ti

Aagt s.

6.2. Unsteady Flow of Internal Incompressible Viscous Flow

In Section 6.1 we ignored the viscous effect of the flow. In this section we solve

the same transient problems while accounting for the viscosity of the fluid.

Flow Oscillation in a U-Tube

Previously, we considered flow oscillations in U-tubes for inviscid fluids. We

now consider a U-tube containing a viscous fluid, initially at rest. The column of

viscous fluid is set in motion by imposition of a pressure difference P

– P

. The

exact solution of viscous flow oscillations in U-tubes is described by Bird. Here

we find an approximate solution by considering an average flow velocity at each

cross section and a friction factor corresponding to the laminar flow. We start

with Equation IIIa.3.42 noting that there is no shaft head. Using the continuity

equation (V

= V

), h

= f(L/D)(V

/2g), and f = 64/Re, we find:

)(

=+−++ V

PPgz

350 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Substituting for V = dz/dt:

0)(

128

=−+++ PP

Rdt

subject to two initial conditions, at t = 0, z = 0 and V = dz/dt = 0. To solve the

above second order non-homogenous differential equation, we substitute for 2z =

s – (P

– P

g to get:

()

(

=++ s

Rdt

Expectedly, this is the general form of the second order differencial equation de-

scribing the oscillation of a damped system such as a linear spring-dash pot sys-

tem or an electrical circuit consisting of resistance, capacitance, and inductance

(RLC circuit). The solution to this homogenous equation can be found by substi-

tuting s = e

Time To Reach Steady-State Flow Rate

Consider the pipe connected to the reservoir of Figure IIIb.6.1(b). The valve is

suddenly opened. We want to find the time it takes for water to reach its steady

state or nominal value for flow rate, considering the friction in the pipe that results

in a head loss. Here, point 1 is taken at the pipe entrance. Hence, V

= V

and Z

= Z

so Equation IIIb.3.42 simplifies to:

0h)(

=+−+

gPPds

Since P

= P

atm

and P

+ P

atm

, the governing equation simplifies to:

−=

Since friction factor is a function of velocity, which in turn is changing with time,

the above first order non-linear differential equation does not in general have an

analytical solution. However, if we treat the friction factor as a constant equal to

its steady-state value, throughout the transient, we find that:

−

IIIb.6.4

where V

is the flow velocity at steady-state condition. Note that velocity ap-

proaches the steady-state value, asymptotically. If we assume that the steady-state

flow rate is reached when V = 0.99 V

then we find the approximate time as t =

2.65LV

/gh

6. Unsteady Internal Incompressible Flow 351

Example IIIb.6.3. The initially closed valve in Figure IIIb.6.1 suddenly opens.

Find the time it takes for the velocity to reach 99% of its final value. Data: L =

3660 m, h

= 24.5 m, d = 63.5 cm, f = 0.02.

Solution: Time is given by t

= 2.65LV

/gh

. But we must first find the steady-

state velocity from:

= f(L/d)

V /2g. Substituting data;

= {[24.5 × 2 × 9.81]/[0.02 × 3660/0.635]}

0.5

= 2 m/s.

Hence, t

= 2.65 × 3660 × 2/(9.81 × 24.5) ≅ 81 s.

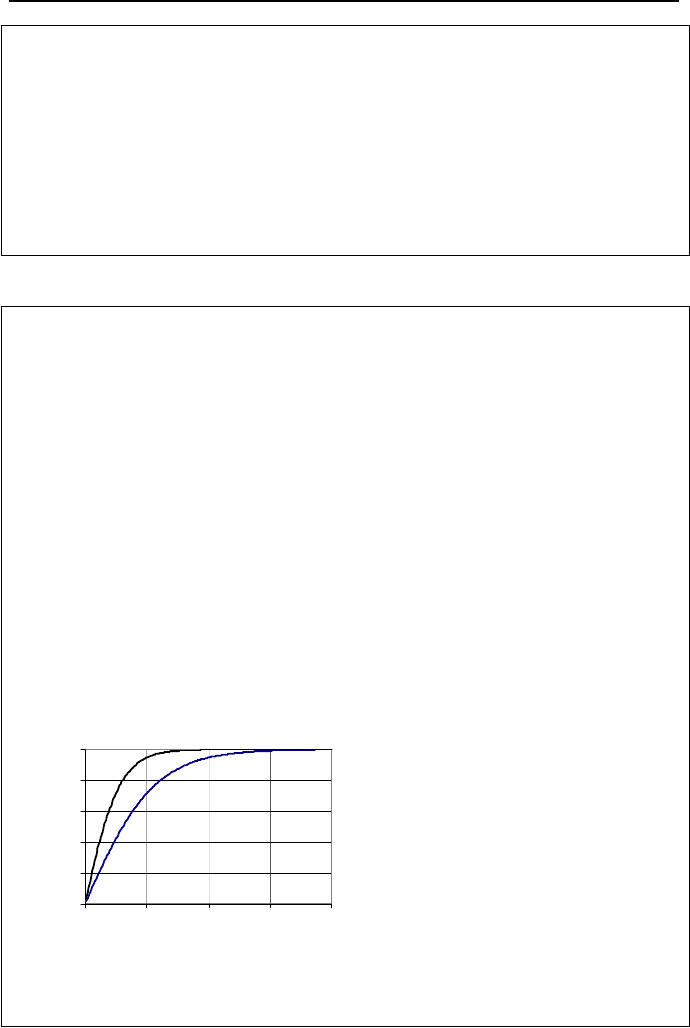
Example IIIb.6.4. Compare time to reach steady-state flow rate for the two cases

of inviscid and viscous flow. Data: L = 100 ft, h

= 20 ft, d = 6 in, f = 0.02.

Solution: First we consider the case of inviscid flow. Equation IIIb.6.2 gives ve-

locity as a function of time

Since V

= (2 × 32.2 × 20)

0.5

= 35.9 ft/s, the velocity ratio becomes:

(V/V

)

inviscid

= tanh(35.9t/200) = tanh(0.18t)

For the case of viscous flow, Equation IIIb.6.4 gives velocity as a function of time.

Rearranging this equation, we obtain V/V

= (e

t/λ

– 1)/(e

+ 1) where λ = LV

/2gh

= [2g h

d/(fL)]

1/2

= {20 × 2 × 32.2]/[0.02 × 100/(6/12)}

0.5

= 18 ft/s

λ = 100 × 18/(2 × 32.2 × 20) = 1.4 s

Hence, the velocity ratio is found as:

(V/V

)

viscous

= (e

t/1.4

– 1)/(e

t/1.4

+ 1)

Velocities versus time are plotted in the figure.

0.2

0.4

0.6

0.8

0 5 10 15 20

Time (s)

V/V

Inviscid

Viscous

As shown in the figure, it takes a longer time for the inviscid flow to establish (i.e.,

flow velocity reaching the steady state value).