Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

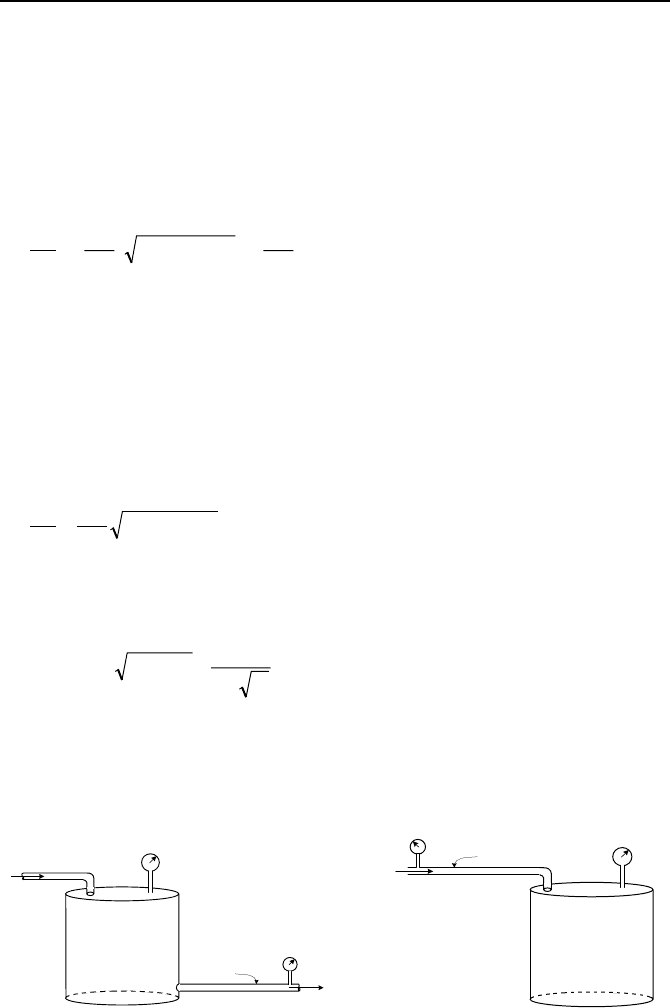
362 IIIb. Fluid Mechanics: Incompressible Viscous Flow
where in Equation IIIb.6.19, the temperature derivative is set equal to zero since
the process is assumed to be isothermal. This is a reasonable assumption if the
tank is not insulated. Equation IIIb.3.7 for momentum balance becomes P – P
C
=
(fL/d)
2
e
m
/(2
ρ
A
2
). Since we have assumed that tank pressure is uniform at all
times, P
B
= P. Furthermore, for this slow gas flow rate we ignored compressibility
effects. Substituting for
e
m
from the momentum balance into Equation IIIb.6.19,
we obtain:
iC
m
RT
PP
RT
dt
dP
¸
¹
·
¨
©
§
−−
¸
¹
·
¨
©
§
+
V
/)(
V
β
IIIb.6.20
where
β
= (fL/d)/(2
ρ
A
2
) and f is treated as a consant. Equation IIIb.6.20 is a non-
linear first order differential equation, predicting the tank pressure as a function of
time, for a specified forcing function for P
C
(t). We can find analytical solution in
closed form for special cases of laminar flow in the pipe or for charging vessels
with no gas withdrawal. For the latter case (i.e.
e
m
= 0, as shown in Fig-
ure IIIb.6.10(b)) the momentum equation for the pipe becomes P
B
– P
C
=
2
i
m
β
. If
we again assume that pressure is uniform in the tank at all times, then P
C
= P.
Substituting in Equation IIIb.6.19 yields:
()
β
/
V
PP
RT
dt
dP
B
−=
an analytical solution exits for charging vessels if the line pressure, P
B
is kept con-
stant:
2
V2
¸
¸
¹
·
¨
¨
©
§
−−−= t
RT
PPPP
oBB
β
IIIb.6.21
The mass flow rate into the tank that results in a tank pressure of P(t) is found
from Equation IIIb.6.19 as:
V
P
T
m
i
.
m
e
.
B
C
L, d, a
P
C
P(t)
V
P
T
m
i
.
P(t)
C
P
B
B
L, d, a
(a) (b)
Figure IIIb.6.10. Pressure of a gas tank to downstream pressure change
6. Unsteady Internal Incompressible Flow 363
t
RT
PP
m
oB
i
V2
ββ
−
−
=
IIIb.6.22
The study of the level response in an open tank holding liquid or the pressure re-
sponse of a tank containing gas to changes in upstream or downstream pressure
showed an interesting phenomenon. It indicated that we may maintain the liquid
level or the gas pressure at specified values by manipulating the upstream or
downstream pressures. Design of the devices which manipulate the upstream and
downstream pressure to maintain level or pressure at specified values are gener-
ally discussed in books on feedback control systems.
Example IIIb.6.6. A tank having a volume of 50 m
3
contains air at 600 kPa. We
intend to charge this tank through a feed line having a diameter of 6 cm and a
length of 35 m. Pressurized air at 1200 kPa and 20 C enters the feed line. Find
the time it takes for the tank pressure to reach 1200 kPa.
Solution: We find time for P(t) = P
B
from Equation IIIb.6.21:
()
β
V2/RT
PP
t
oB
−
=
P
B
= 1200 kPa, P
o
= 600 kPa, R = 8314/28.97 = 287 m N/kg K, V = 50 m
3
, T =
273 + 20 = 293 K,
ρ
=
P
/(RT) = 900/(0.287 × 293) = 10.7 kg/m
3
β
= (fL/d)/(2
ρ
A
2
) = 0.012 × 35/[2 × 0.06 × 10.7 × (
π
× 0.06
2
/4)
2
] = 0.41E5 (m kg)
–
1
Substituting, we find:
t = 1000)6001200( ×− /[287 × 293/(2 × 50 × 5E41.0 )] = 186.5 s.
Vent Clearing, Liquid Expulsion
Our goal is to determine the time for liquid expulsion from a submerged pipe,
which is also referred to as vent clearing. As shown in Figure IIIb.6.11(a), a pipe
of constant cross sectional area A, is submerged in a liquid pool while connected
to a reservoir of pressurized gas or vapor, having pressure P
g
. As an example, this
situation may represent the discharge of steam into the subcooled water of a BWR
suppression pool. Our control volume extends from point 1 to point 2. As before,
we use the same conservation equations for mass and momentum to determine the
time for liquid expulsion from the pipe. The implicit assumption in this derivation
is that the propagation time (t
p
= L/c where c is the speed of sound) is much
shorter than the expulsion time. We apply Equation IIIa.3.44 to the control vol-
ume, with terms expanded below:
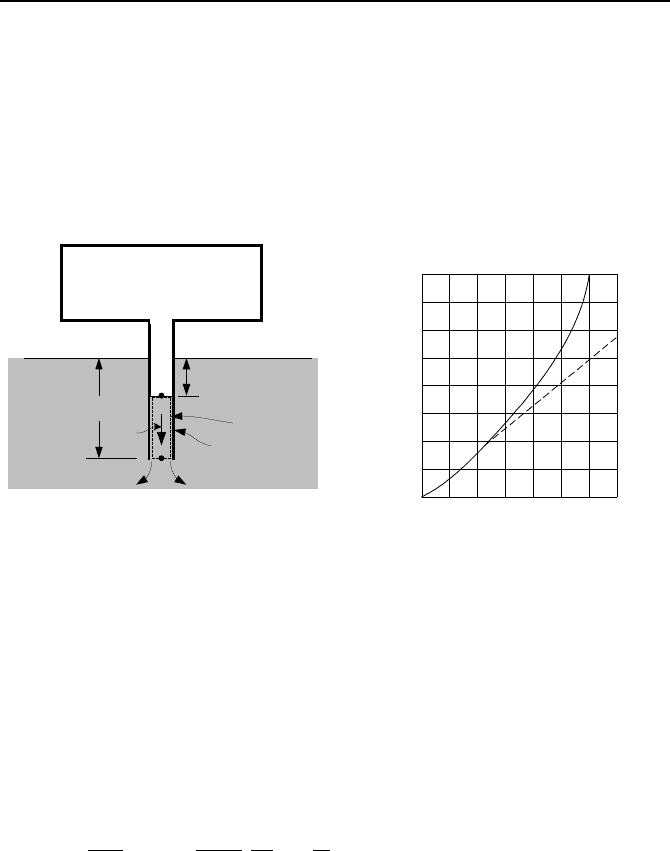
364 IIIb. Fluid Mechanics: Incompressible Viscous Flow
∆P
inertia
=
ρ
(H – s)dV/dt
∆P
pump
= 0
∆P
stat
= P
2
– P
1
∆P
vel
= 0
∆P
grav
=
ρ
g(Z
2
– Z
1
)
∆P
fric
= f[(Η
−
s)/d]
ρ
V
2
/2
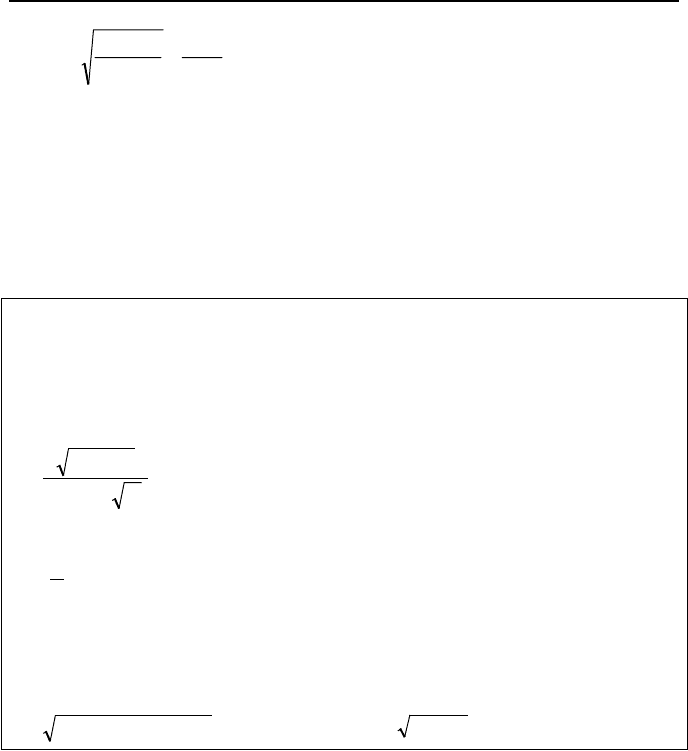
s
H
1
2
Pressurized Gas or Vapor
P
f
P
g
ρ
d,
A
Control
Volume
V
Free stream
0
0.5
1.0
1.5
2.0
0
0.4 0.8
1.4
1.2
1.00.2 0.6
t
ξ/
Η
V/
ξ
(a) (b)
Figure IIIb.6.11. Expulsion of liquid from a submerged pipe
Since the gas density is generally negligible, P
1
= P
g
. Also, from a simple force
balance we find that:
P
2
= P
f
+
ρ
gH
We also note that Z
2
– Z
1
= (s – H). The conservation equation of mass takes the
form of V = ds/dt. If we substitute for P
1
, P
2
, Z
2
– Z
1
, and V in Equation IIIa.3.44,
we obtain:
)(
1
)(
H
)H(
2
2
2
fg
PP
dt
ds
d
s
fgs
dt
sd
s
−=
−
++−
ρ
IIIb.6.23
where in Equation IIIb.6.23, P
f
is the free stream pressure. For the initial condi-
tion, we assume s is known. For example, if the pipe is full of water up to height
H then s(t = 0) = 0. Also at time zero, liquid is at rest hence, ds(t = 0)/dy = 0. The
solution to Equation IIIb.6.23 depends on the manner in which P
g
is increased to
expel liquid. Moody obtained solution for the cases of step increase (P
g
= P
o
) as
well as a ramp increase (P
g
= P
f
+ Ct, where C is a positive constant). The solu-
tion for the step increase in pressure is given as:
6. Unsteady Internal Incompressible Flow 365
2
H
H
ln
2
1
2
¸
¹
·
¨
©
§
−
¸
¸
¹
·
¨
¨
©
§
=
s
erf
L
t
π
ξ
IIIb.6.24
where
ξ
=
ρ
/)(
fo
PP − and the error function, erf(x), is defined in Chap-
ter VIIb.3. Values of erf(x) are given in Figure IVa.9.3. Equation IIIb.6.24 is
plotted with the solid line in Figure IIIb.6.11(b). The time to expel all the liquid
from the pipe is found by letting s approach H:
θ
= 1.253H/
ξ
IIIb.6.25
The dotted line in Figure IIIb.6.11(b) is for a case where the step increase in pres-
sure is just enough to push the liquid to the exit of the pipe. The step increase in
this case is for P
g
to be increased to P’ = P
f
+
ρ
gH.
An interesting observation is that for cases where P
g
> P’, velocity increases
rapidly as s approaches H. Indeed Equation IIIb.6.24 shows that the denominator
becomes zero. This is expected, as the mass of liquid approaches zero. In reality,
the mass expelled from the pipe would accelerate the surrounding liquid, which
was not considered in the above analysis. Thus, real velocity remains at a finite
value.
Dynamics of Gas Bubbles
Analysis of rising bubbles in liquids is an involved task and the phenomenon is
still a topic of investigation. The reason is due to the associated complexities such
as; bubble shape, friction force (referred to as drag), geometry of the liquid con-
tainer (bubble rise in an infinite liquid versus in a bank of tubes), liquid motion
(stagnant versus flowing liquid), type of process (adiabatic versus thermal), and
gas diffusion into liquid.
Gas bubbles are introduced into a liquid whereas vapor bubbles are primarily
induced into the liquid such as in boiling. Here we discuss only gas bubbles.
Steam bubbles are discussed in Chapter Vb.
h
Hd
y
d
i
F
D
F
B
F
W
Figure IIIb.6.12. Gas bubble rising in a pool of liquid

366 IIIb. Fluid Mechanics: Incompressible Viscous Flow
Let’s consider a simple case of a single non-condensable spherical
*
gas bubble
in infinite stagnant water. Our goal is to find the bubble velocity and diameter as
a function of time while the bubble is rising to the liquid surface. To obtain an
analytical solution in closed form, we make several simplifying assumptions,
which limit the results to cases for which the assumptions are valid. Suppose a
small nitrogen bubble (3 mm
≤ d
i
≤ 9 mm) is just released in a pool of water at
elevation H below the water surface. Due to buoyancy, the bubble rises to the sur-
face while friction in the form of the drag force resists the bubble motion. The net
force acting on the bubble results in the acceleration of the bubble according to
Newton’s second law. If the bubble trajectory does not significantly deviate from
the vertical, then the bubble acceleration is along the y-axis:
F
B
– F
W
+ F
D
= m
b
a
y
IIIb.6.26
where subscripts B, W, D, and b stand for buoyancy, weight, drag, and bubble, re-
spectively. We now assume that after the initial acceleration period, the bubble
reaches a terminal velocity at which point a
y
= 0. All then we need to do is to ex-
press F
B
, F
W
, and F
D
in terms of the system parameters. The bubble weight is
found from F
W
=
ρ
b
Vg where V is the bubble volume. The buoyancy force arises
as a result of the displaced water by the presence of the bubble. Therefore, F
B
=
ρ
w
Vg where subscript w stands for water. The drag force is due to frictional pres-
sure drop; F
D
= (∆P)A
b
where A
b
in this relation is the projected area of the spheri-
cal bubble, A
b
=
π
d
2
/4 where d is the bubble diameter. Pressure drop, due to drag
on the bubble, is similar to Equation IIIb.3.11. Therefore, the drag force on the
bubble, F
D
becomes:
()
4/
2
2
2
d
V
CPAF
w
DbD
π
ρ
¸
¸
¹
·
¨
¨
©
§
=∆= IIIb.6.27
where in Equation IIIb.6.27, C
D
is the drag coefficient. Solution of Equa-
tion IIIb.6.26 depends on the expression used for the drag coefficient, which in
turn depends on a variety of factors such as bubble velocity and liquid properties
(viscosity, density, and liquid surface tension). For laminar flow, C
D
= 16/Re
where Re =
ρ
w
Vd/
µ
w
. Substituting C
D
into Equation IIIb.6.27, we find F
D
=
2
πµ
Vd. Stokes derived the drag force for very low Re numbers with negligible
inertial forces as F
D
= 3
πµ
Vd (Fox). Substituting the Stokes drag force in Equa-
tion IIIb.6.26, noting that
ρ
b
<<
ρ
w
, and substituting the results in Equa-
tion IIIb.6.26 (with a
y
= 0), we find
ρ
w
Vg = 3
πµ
Vd. Solving for the terminal ve-
locity, we get:
µ
ρ
18
2
gd
V
w
= IIIb.6.28
As the bubble rises, pressure keeps dropping thus d changes with time and so does
the bubble velocity. To express d as a function of time, we use the equation of
*
An aspect ratio is defined for elliposoidal bubbles, given as the ratio of the bubble minor
over its major axis. For spherical bubbles the aspect ratio is unity.

6. Unsteady Internal Incompressible Flow 367
state for the isothermal bubble. At any depth along the buble flow path; PV = P
i
V
i
where i refers to the bubble initially released at depth H. Substituting for V =
π
d
3
/6 and for P =P
atm
+
ρ
w
gh in the equation of state, the bubble diameter is found
as:
i
watm
i
d
gP
P
d
3/1
h
¸
¸
¹
·
¨
¨
©
§
+
=
ρ
IIIb.6.29
where d
i
is the initial bubble diameter at depth H. Substituting Equation IIIb.6.29
into Equation IIIb.6.28, we find the bubble velocity as a function of time. How-
ever, these are implicit relations in time as h = f(t), is yet to be determined. To
find h, we use the fact that dh/dt = V with the initial condition of h(t = 0) = H.
Substituting from Equations IIIb.6.28 and IIIb.6.29 and integrating, we find h as a
function of time given by:
»
»
»
¼
º
«
«
«
¬
ª
−
¸
¸
¹
·
¨
¨
©
§
−=
atm
iw
i
w
Pt
gd
P
g
5/3
2
3/5
54
)(5
1
h
µ
ρ
ρ
IIIb.6.30
where P =P
atm
+
ρ
w
gH. We then find V = f(t) and d = f(t) by back substitution of
Equation IIIb.6.30 into Equations IIIb.6.29 and the result in III.6.28, respectively.
Flow Distribution in Piping Networks, the Nahavandi Method
Two methods for determination of flow distribution in piping networks were dis-
cussed in Section 3. Here, we discuss the Nahavandi method, which is based on
solving the transient form of the conservation equations of mass and momentum.
To determine flow under steady-state condition, a null transient is analyzed. The
null transient, also known as dynamic relaxation, finds solutions for time depend-
ent problems without any imposed forcing function in the boundary conditions. In
this method, the same concept of node and inter-nodal flow path, branch, or link,
as discussed in Section 3 applies. The continuity equation is applied to each node
and the momentum equation to each flow path. However, no mass storage at a
node or in a flow path is allowed. This assumption, while greatly simplifying the
analysis, introduce only slight inaccuracy if applied to incompressible flow. Addi-
tionally, the liquid must remain single-phase as no heat transfer is considered in
the network. Since the method is applicable only to slow transients, the wave
propagation effect, as discussed in Section 7 is also neglected. The Nahavandi
method is well suited for computer programming since the formulation is based on
matrix algebra.
The Continuity Equation: To write the continuity equation in matrix form,
we first define a connection matrix [C] with elements being either +1, –1, or 0.
This matrix is obtained from the fact that pressure drop between two nodes is re-
lated to the nodal pressures as:
{
∆P
stat
} = –[C] {P} IIIb.6.31
368 IIIb. Fluid Mechanics: Incompressible Viscous Flow
where the number of rows of matrix [C] is equal to the number of branches and
the number of columns in matrix A is equal to the number of nodes of the piping
network. In Equation IIIb.6.31, a matrix is represented by [ ] and an array by { }.
Matrix algebra is discussed in Chapter VIId.
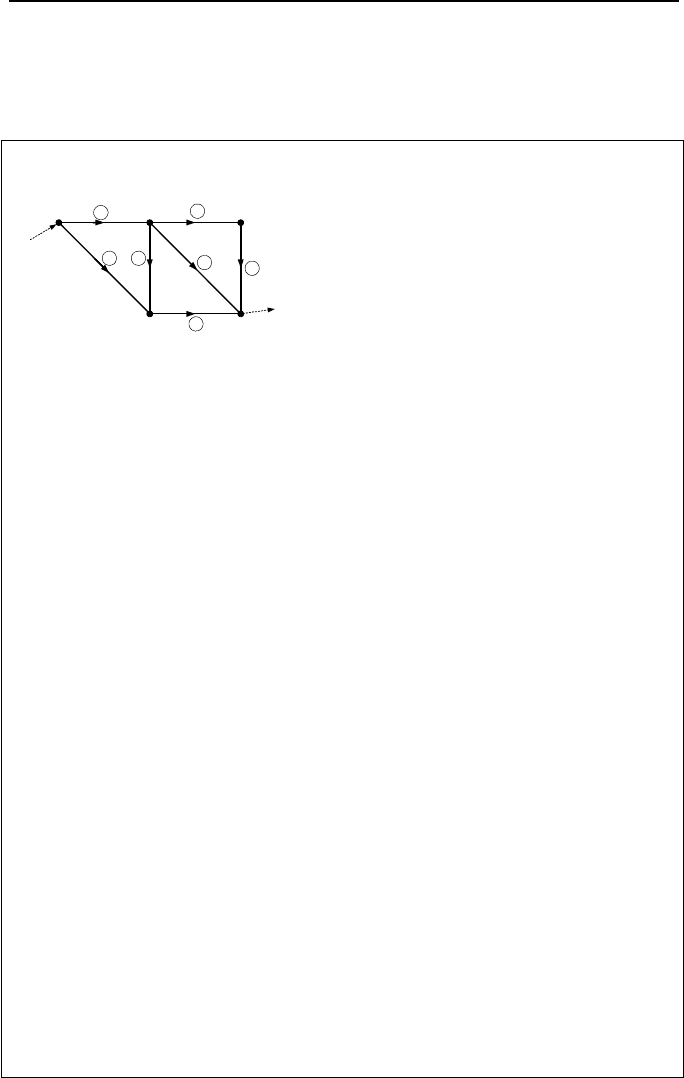
Example IIIb.6.7. Find the connection matrix for the piping network shown in
the figure.
1
3
2
5
4
1
5
4
32
Supply
Output
1
m
5X
m
1X
m
7
6
Solution: There are 5 nodes and 7 flow paths. To distinguish the number repre-
senting a node from the number representing a flow path, the latter is placed inside
a circle next to the related flow path. The flow to node 1 is from a source for
which the source pressure is given. The output flow rate to a sink is from node 5.
Subscript X indicates that the flow is an external flow (i.e., enters or leaves the pip-
ing network). The supply pressure and the external flow are given and we must
find the unknown inter-nodal flow rates. Recall that according to our sign conven-
tion, any flow leaving a node would be assigned a plus and any flow entering a
node would be assigned a minus sign. Pressure drop is related to nodal pressure
through ∆P = P
B
– P
A
:
∆P
1
= ∆P
1 – 2
= –(P
1
– P
2
)
∆P
2
= ∆P
1 – 3
= – (P
1
– P
3
)
∆P
3
= ∆P
2 – 3
= – (P
2
– P
3
)
∆P
4
= ∆P
2 – 4
= – (P
2
– P
4
)
∆P
5
= ∆P
2 – 5
= – (P
2
– P
5
)
∆P
6
= ∆P
3 – 5
= – (P
3
– P
5
)
∆P
7
= ∆P
4 – 5
= – (P
4
– P
5
)
Hence, Equation IIIb.6.31 becomes:
°
°
°
¿
°
°
°
¾
½
°
°
°
¯
°
°
°
®
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
¬
ª
−
−
−
−
−
−
−
−=
°
°
°
°
¿
°
°
°
°
¾
½
°
°
°
°
¯
°
°
°
°
®
∆
∆
∆
∆
∆
∆
∆
5
4
3
2
1
7
6
5
4
3
2
1
11000
10100
10010
01010
00110
00101
00011
P
P
P
P
P
P
P
P
P
P
P
P
The connection matrix is thus a 7 × 5 matrix with elements of only –1, 1, and 0

6. Unsteady Internal Incompressible Flow 369
Having determined the connection matrix [C], the continuity equation for the
piping network becomes:
[]
{} { } {}
0=+
X
T
mmC
IIIb.6.32
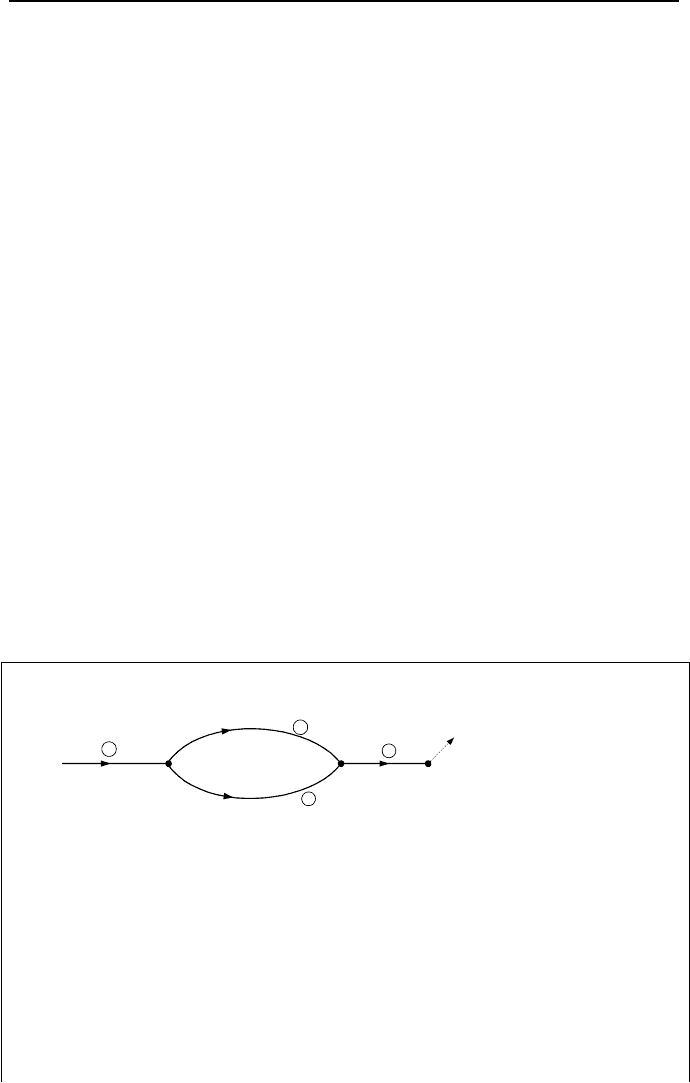
Example IIIb.6.8. For the piping network of Example IIIb.6.7, verify the
Kirchhoff’s law for nodes 2 and 5.
Solution: To verify Equation IIIb.6.32, we need to find the transpose of matrix C
and multiply it by the mass flow rates while considering the output flows:
°
°
°
¿
°
°
°
¾
½
°
°
°
¯
°
°
°
®
=
°
°
°
¿
°
°
°
¾
½
°
°
°
¯
°
°
°
®
−
+
°
°
°
°
¿
°
°
°
°
¾
½
°
°
°
°
¯
°
°
°
°
®
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
¬
ª
−−−
−
−−
−
0
0
0
0
0
0
0
0
1110000
1001000
01001
10
0011101
0000011
5
1
7
6
5
4
3
2
1
X
X
m
m
m
m
m
m
m
m
m
From this matrix equation, we get confirmation that for node 2, for example:
0
5431
=+++− mmmm
Similarly for node 5 we have:
0
5765
=+−+−−
X
mmmm
A piping network having N nodes and M flow paths has a total of M + N un-
knowns. These are N nodal pressures and M flow rates. There are N continuity
equations given by Equation IIIb.6.32 and M momentum equations written for the
M flow paths as discussed next.
The Momentum Equation: We may use Equation IIIa.3.44 for each flow
path:
)()(
fricacclgravstatpump
PPPPP
dt
md
A
L
∆+∆+∆+∆−∆=
¦
Approximating the time dependent term by finite difference and multiplying both
sides by A/L we obtain:
¿
¾
½
¯
®
=
¿
¾
½
¯
®
∆
−
+
L
A
t
mm
nn
1
{
}
](
fricgravvelstatpump
PPPPP ∆+∆+∆+∆−∆ IIIb.6.33
where various pressure terms in Equation IIIb.6.33 are defined in Equa-
tion IIIb.4.1. Note that in Equation IIIb.6.33, the mass flow rates with superscript
370 IIIb. Fluid Mechanics: Incompressible Viscous Flow
n+1 are the unknown mass flow rates to be calculateded at time n + 1 having mass
flow rates at time n. Mass flow rates at time zero are obtained from our initial
guesses based on engineering judgment. These estimated flow rates must satisfy
the Kirchhof’s law at each node. We now rearrange Equation IIIb.6.33 for the un-
known mass flow rates:
{}{}
(){}
fricgravstatpump
nn
PPBPPBmm ∆+∆−∆−∆+=
+
)(
1
IIIb.6.34
where in Equation IIIb.6.34, {B} = {A
i
∆t/L
i
} with A representing the flow area and
L the flow length.
Matrix Solution: To find nodal pressures, we substitute for {
∆P
stat
} from
Equation IIIb.6.31 into Equation IIIb.6.34 and then substitute the resulting equa-
tion into Equation IIIb.6.32 to obtain:
[]
{
}
[][][]
{}
[]
(){}
{}{}
0=+∆+∆−∆++
Xfricgravpump
TT
n
T
mPPBPBCPCBCmC
IIIb.6.35
We can now solve Equation IIIb.6.35 for the unknown nodal pressures. The solu-
tion is as follows:
{}
[] []
()
{
}
[]
{}
X
n
fricgravpump
T
mEmPPBPBCEP
11 −−
−−∆+∆−∆= IIIb.6.36
where in Equation IIIb.6.36, [E] = [C]
T
[B][C] is a square matrix and [B] a diagonal
matrix with diagonal elements of [B
i
] = {A
i
∆t/L
i
}. Having found nodal pressures,
we can find inter-nodal flow rates from Equation IIIb.6.34.
Example IIIb.6.9. Determine matrix [E] for the network shown in the figure.
123
Supply
Output
1
2
3
4
Solution: Using the supply pressure as the reference pressure, we find ∆P
1
= – (0
– P
1
). Thus we find:
°
¿
°
¾
½
°
¯
°
®
»
»
»
»
¼
º
«
«
«
«
¬
ª
−
−
−
−
−=
°
°
¿
°
°
¾
½
°
°
¯
°
°
®
∆
∆
∆
∆
3
2
1
4
3
2
1
110
011
011
001
P
P
P
P
P
P
P
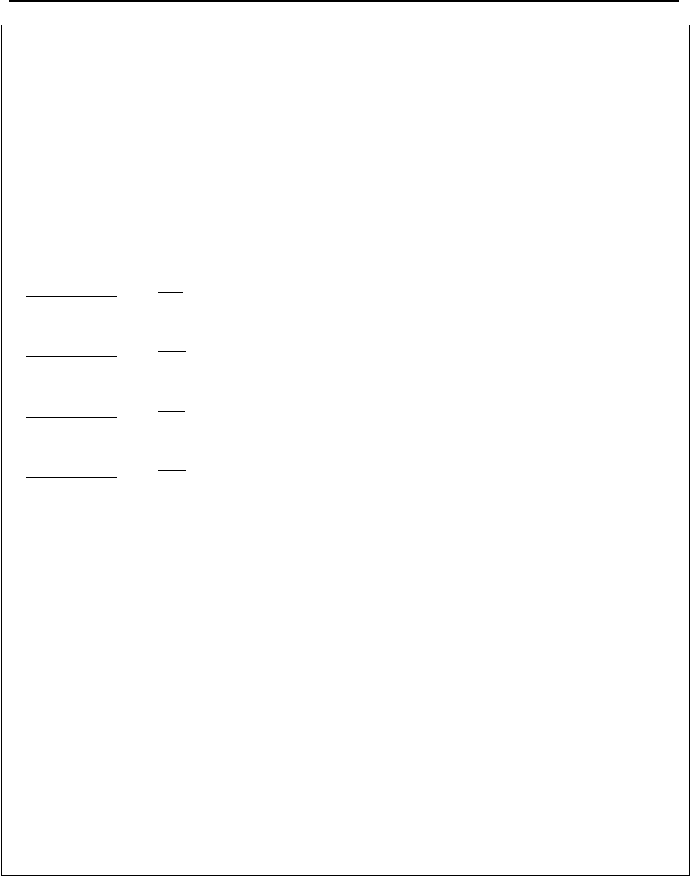
7. Fundamentals of Waterhammer Transients 371
Using the connection matrix, the continuity equation becomes:
°
¿
°
¾
½
°
¯
°
®
=
°
¿
°
¾
½
°
¯
°
®
+
°
°
¿
°
°
¾
½
°
°
¯
°
°
®
»
»
»
¼
º
«
«
«
¬
ª
−
−−
−
0
0
0
0
0
1000
1110
0111
3
4
3
2
1
x
m
m
m
m
m
The momentum equation becomes:
()
()
()
()
°
°
°
°
°
¿
°
°
°
°
°
¾
½
°
°
°
°
°
¯
°
°
°
°
°
®
∆−∆−∆−∆
∆−∆−∆−∆
∆−∆−∆−∆
∆−∆−∆−∆
=
°
°
°
°
°
¿
°
°
°
°
°
¾
½
°
°
°
°
°
¯
°
°
°
°
°
®
∆
−
∆
−
∆
−
∆
−
+
+
+
+
444
4
4
333
3
3
222
2
2
111
1
1
4
1
4
3
1
3
2
1
2
1
1
1
fricgravpump
fricgravpump
fricgravpump
fricgravpump
nn
nn
nn
nn
PPPP
L
A
PPPP
L
A
PPPP
L
A
PPPP
L
A
t
mm
t
mm
t
mm
t
mm
The [E] matrix is obtained from:
[]
()
»
»
»
»
¼
º
«
«
«
«
¬
ª
−
−
−
−
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
−
−−
−
∆=
110
011
011
001
/000
0/00
00/0
000/
1000
1110
0111
44
33
22
11
LA
LA
LA
LA
tgE
Thus the elements of the [E] matrix are:
[]
()
()()() ()()
()()()()()()
() ()
»
»
»
¼
º
«
«
«
¬
ª
−
−++−−
−−++
∆=
4444
444433223322
3322332211
//0
//////
0/////
LALA
LALALALALALA
LALALALALA
tgE
We can then find the nodal pressures by inverting matrix [E], substituting the re-
sults into Equation IIIb.6.36, and performing the matrix operations.
7. Fundamentals of Waterhammer Transients
Analysis of waterhammer or rapid flow transients, where acoustic waves travel
through the flow path, is much more involved than the rigid column theory. In
this section we just introduce the concept of waterhammer analysis for liquids
only and discuss some preliminary derivations of governing equations. For more
information on this topic, the interested reader may review works of Parmakian,
