Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

372 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Watters, and Wiley & Streeter. An added complication in waterhammer analysis,

in addition to the effects of fluid compressibility, is the fact that the elasticity of

the conduit containing the fluid must also be taken into account. For this reason,

waterhammer analysis is also called elastic analysis.

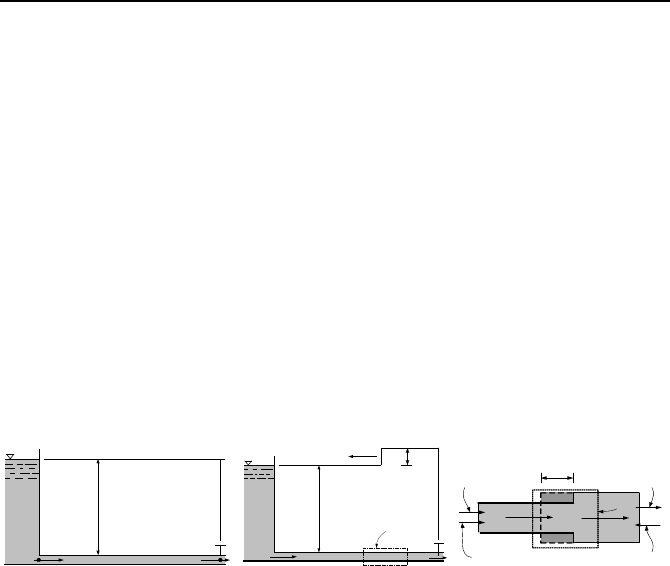
To introduce the concept of rapid transient analysis, let’s consider a simple case

of steady fluid flow in a frictionless horizontal pipe at a speed of V

, as shown in

Figure IIIb.7.1(a). Since the pipe is frictionless, pressure head at point B, where a

control valve is located, is the same as that of point A hence, the hydraulic grade

line (HGL) is horizontal. Our goal is to find the pressure head caused by throttling

of the valve. In Figure IIIb.7.1(b), the valve is instantaneously throttled so that

flow velocity has dropped to V

< V

. The reduction in flow velocity, according to

the Bernoulli equation is associated with an increase in pressure head just up-

stream of the valve. The increased pressure head is now a driving force, which

causes the disturbance to travel upstream of the valve at the acoustic velocity in

the medium, c. The increased pressure head (∆H) also affects the liquid via com-

pression and the pipe wall via expansion.

HGL

∆H

-c

L = (c - V

)∆t

(

A)V

(

A)V

gHA

g(H+∆H)A

(a) (b) (c)

Figure IIIb.7.1. Flow from a reservoir through a frictionless pipe.

We now write the momentum equation for a control volume through which the

disturbance would pass as shown in Figure IIIb.7.1(c). The summation of all the

forces is equal to the rate of change of momentum in the control volume, plus the

net momentum flux per Equation IIIa.3.6. Net force is found as:

–

gHA –

g(H + ∆H)A = –

gA∆H

Note that we ignored the slight increase in the pipe flow area due to expansion.

Net momentum flux is obtained as [

AVAV

ρρ

−

]. Throttling of the valve has

resulted in a

∆V reduction in the flow velocity therefore, ∆V = V

– V

. Substitut-

ing for V

and ignoring ∆V

, momentum flux reduces to:

AVAV

[

ρρ

− ] = AVAVV

)([

ρρ

−∆− ] ≅ –(2

∆V

)

Finally, we find the rate of change of momentum as follows. We note that flow is

moving at a velocity of V

towards the right and the disturbance is moving at the

speed of sound in the liquid towards the left. Hence, at the time increment

∆t, the

control volume has a length of (c – V

)∆t and a mass of

(c – V

)∆tA. In the inter-

7. Fundamentals of Waterhammer Transients 373

val ∆t, velocity has changed from V

to V

. Hence, the rate of change of momen-

tum is given by [

g(c – V

)∆tA][(V

– V

)/∆t]. The momentum equation for the

control volume becomes:

–

gA∆H = [

g(c – V

)∆tA](–∆V/∆t) –(2

∆V

)

This simplifies to:

∆H = c∆V(1 + V

/c)/g IIIb.7.1

We can further simplify this relation by comparing typical flow velocities with the

speed of sound in various mediums as shown in Table IIIb.7.1. Hence, ignoring

/c as compared with unity, we find ∆H ≅ c∆V/g.

Example IIIb.7.1. Flow velocity of a liquid, for which c = 4900 ft/s, is reduced

from 2 ft/s to 1 ft/s. Find the resulting head rise.

Solution: From Equation IIIb.7.1, since V << c, we find ∆H = 4900 × (2 – 1)/32.2

= 152 ft. This is a substantial rise in head for such a small change in flow rate in-

dicating that waterhammer subjects piping to a large magnitude force with poten-

tial of damaging the piping system. If the liquid is water, then ∆P ≅ 66 psi.

The magnitude of waterhammer forces depends on the elasticity of the piping

material and liquid compressibility. The more rigid the piping material, the higher

the magnitude of the waterhammer force. As for liquid compressibility, the lower

the compressibility, the higher the waterhammer force. Equation IIIb.7.1 can be

extended to multiple incremental changes of velocity. In particular,

≅Σc∆V/g IIIb.7.2

Here we ignored pipe friction as well as any reflecting wave traveling towards the

regulating valve. In a more rigorous analysis, we shall consider both pipe friction

and forward and reflecting waves due to pressure wave propagation. However, we

first discuss effects of various parameters on the wave speed.

7.1. Factors Affecting The Speed of Acoustic Waves

Speed of sound in several mediums is shown in Table IIIb.7.1. In liquid flow in-

side pipes, the wave speed depends not only on the elasticity of the piping material

but also on such parameters as diameter and thickness of the pipe as well as den-

sity and bulk modulus of the liquid. To mathematically demonstrate the depend-

ency of the sound wave on these parameters we consider flow of a liquid in the

pipe of Figure IIIb.7.1 with valve instantly shut. In this case, V

= 0 and ∆V = V

Instant closure of the valve results in development of a pressure head, which com-

presses the liquid and causes the pipe to expand both axially and in the radial di-

rection. However, axial direction is generally much smaller as compared with ra-

dial expansion of the pipe. Expansion of the pipe combined with compression of

the liquid result in a certain amount of the liquid mass from the reservoir entering

374 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Table IIIb.7.1. Speed of sound in various mediums

the pipe. This amount of mass can be found from the following mass balance. If

L is the length of the pipe, it takes t = L/c seconds for the pressure wave to reach

the reservoir after the instant closure of the valve. During this time, a total of

(

A)L/c mass of liquid has entered the pipe. The mass of liquid entering the

pipe due to pipe expansion is

L∆A and the mass entering due to liquid compres-

sion is LA

∆

. Therefore,

(

A) L/c =

L∆A + LA∆

This equation simplifies to V

/c = ∆A/A + ∆

. Noting that V

= ∆V, we substi-

tute for

∆V from Equation IIIb.7.1 for V

<< c and solve for c

to obtain:

= g∆H/[∆A/A + ∆

] IIIb.7.3

To relate the wave speed to the liquid and the pipe wall properties, we first replace

∆H = ∆P/

(g/g

) and take advantage of the definition of liquid bulk modulus, as

defined in Chapter IIIa, E

= ∆P/(∆

). Equation IIIb.7.3 becomes:

= (E

)/[1 + E

∆A/A∆P] IIIb.7.4

Now, we canrelate

∆P and ∆A/A to pipe properties. To do this, we consider the

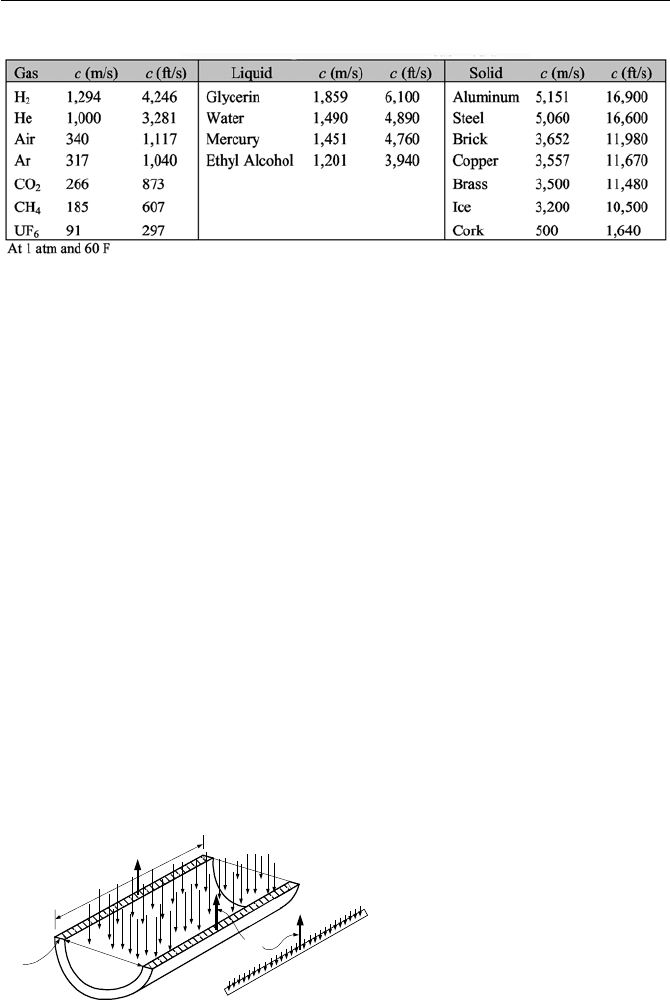
free body diagram of the pipe as shown in Figure IIIb.7.2 and perform a simple

force balance.

∆F

∆P

Figure IIIb.7.2. The free body diagram of a pipe carrying fluid

7. Fundamentals of Waterhammer Transients 375

The incremental internal pressure in the pipe is balanced by the circumferential

tensile force per unit length; 2

∆FL = ∆P(LD). Since the incremental tensile force

in turn is balanced by the tensile stress

∆FL=

), then we can relate stress to

incremental pressure 2

σδ

= ∆PD or

= ∆PD/

. Having related ∆P to pipe

stress, we seek to relate

∆A to pipe strain. We then would relate strain to stress

through E, the modulus of elasticity as

/E. The incremental increase in flow

area is given by

∆A =

D (∆D/2). But by definition,

= ∆D/D. Hence, ∆A =

/2. We now substitute for

in terms of

and for

in terms of ∆P to get;

∆A/A = ∆PD/E

. Substituting in Equation IIIb.7.4, we obtain:

[]

()

[]

2/1

1/)/)(/(1/)/(

PipeLiquid

CCDEEEc +=+=

δρ

IIIb.7.5

where we have called g

= C

Liquid

and (E

/E)(D/

) = C

Pipe

. Elasticity of some

piping materials is given in Table IIIb.7.2.

Table IIIb.7.2. Elasticity for some piping materials

Example IIIb.7.2. Water at 60 F is flowing in a 22-inch Schedule 60 steel pipe.

Find the wave speed for the system.

water

= 62.37 lbm/ft

, (E

)

water

= 3.11 × 10

psi and E

steel

= 30 × 10

psi.

Solution: For 22-inch Schedule 60 pipe, D = 20.25 in and

= 0.875 in. From

Equation IIIb.7.5 we have:

ft/s4318

)875.0/25.20)(7E3/5E11.3(1

37.62/)5E11.3144(2.32

××

If the pipe was fully rigid (i.e., ∞→E ), then the wave speed would have been

found from:

Ec = ft/s480837.62/5E11.31442.32 =××=

Speed of sound in water from Table IIIb.7.1 is 4890 ft/s.

To determine the effect of wall thickness, we may perform similar analysis as

in Example IIIb.7.1 with wall thickness as a variable. The results of such analysis

for two types of piping materials are shown in Table IIIb.7.3.

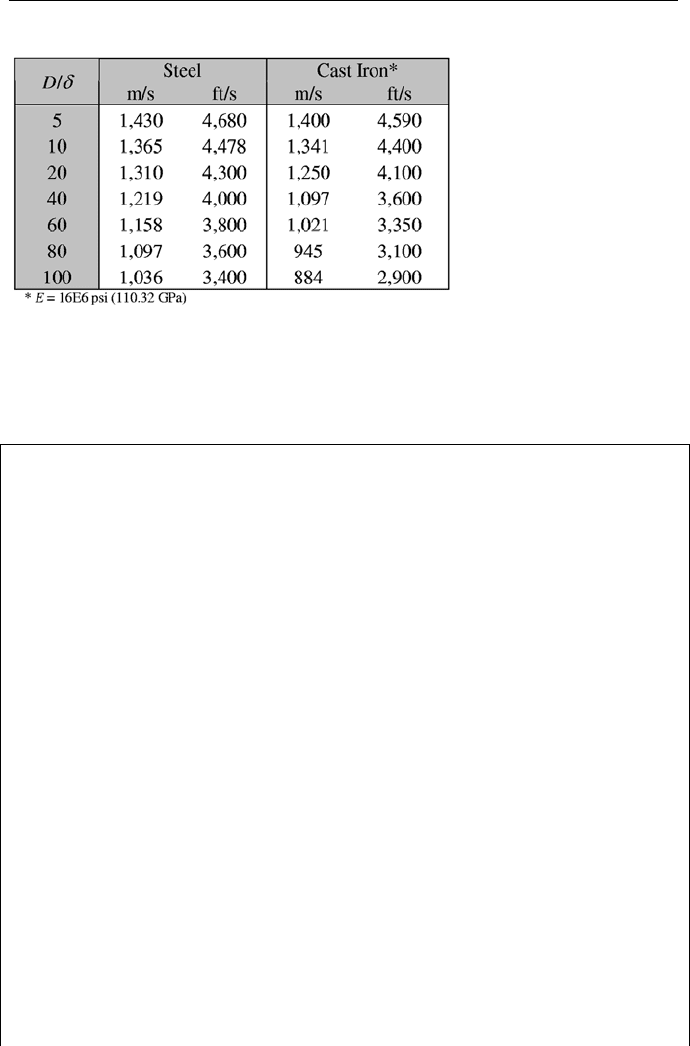
376 IIIb. Fluid Mechanics: Incompressible Viscous Flow

Table IIIb.7.3. Wave speed in piping systems

Having the wave speed enables us to compare the head rise subsequent to sud-

den closure of a valve in various piping systems. In the example below, we com-

pare the head rise in two piping systems.

Example IIIb.7.3. Water flows at 80 F in a 20-inch Schedule 40 pipe. Find the

head rise due to instantaneous closure of a valve (a) for steel pipe and (b) for a

PVC pipe having the same dimensions as the steel pipe.

water

= 62.22 lbm/ft

)

water

= 3.22E5 psi. Water flow rate is 5198 GPM.

Solution: For a 20 in (51 cm) nominal pipe size Schedule 40, D = 18.812 in (48

cm),

= 0.594 in (1.5 cm), E

steel

= 30E6 psi (206.85 GPa) and E

PVC

= 4E5 psi

(2.758 GPa). For the steel pipe, we calculate:

Pipe

)

Steel

= (E

/E)(D/

) = 1 + (3.22/300)(18.812/0.594) = 0.34

and for the PVC pipe, we have:

Pipe

)

PVC

= (E

/E)(D/

) = 1 + (3.22/4)(18.812/0.594) = 25.49

For both cases:

Liquid

= E

= 32.2 × (144 × 3.22E5/62.22) = 24E6

The wave speed for the steel pipe is found as:

()

[]

2/1

PipeLiquid

CCc += = [24E6/(1 + 0.34)]

0.5

= 4232 ft/s (1290 m/s)

and for the PVC pipe as:

()

[]

2/1

PipeLiquid

CCc += = [24E6/(1 + 25.49)]

0.5

= 970 ft/s (296 m/s)

Water velocity is found as:

7. Fundamentals of Waterhammer Transients 377

V =

Pipe

A/V



=[5198/(60 × 7.481)]/[

(18.812/12)

/4] = 6 ft/s (1.83 m/s)

Hence, the head rise from Equation IIIb.7.1 for V << c, i.e., ∆H ≅ c∆V/g for flow

in the steel pipe is:

∆H ≅ c∆V/g = 4232 × 6/32.2 = 788.6 ft (240.3 m)

In the case of the PVC pipe we find the head rise as:

∆H ≅ c∆V/g = 970 × 6/32.2 = 180 ft (55 m)

So far we noticed how analysis of a fast transient differs from the rigid column

theory. We performed some hand calculations to determine the head rise follow-

ing instantaneous closure of a valve. We were also able to express the speed by

which disturbances in a fluid are propagated in terms of the factors affecting it.

Next, we perform a more rigorous analysis to obtain the conservation equations in

the form of partial differential equations. To be able to solve the set of governing

equations, we use the method of characteristics. This method allows us to solve

the converted equations by finite difference.

7.2. Analysis of Fast Transients in Piping Systems

Our goal is to analyze the response of a piping system containing the flow of a

fluid to a fast transient. For this purpose, we consider the internal, one-dimension-

al flow of a fluid in a pipe. The free body diagram of an element of this piping

system is shown in Figure IIIb.7.3. In general, the pipe may have an angle

with

the horizontal plane. Initially, fluid is flowing steadily in the pipe. At time zero, a

valve is instantly closed causing in pressure waves to propagate at the speed of

sound in the system. As a result of the perturbation, the fluid is compressed and

the pipe expands. We now set up the conservation equations of mass and momen-

tum for the elemental control volume assuming that the elongation in the axial di-

rection is negligible compared with the elongation in the radial direction.

∆F

Weight

= ∆Mg

∆x

∆F

Wall

πτ

∆xD

P(x)A

P(x+∆x)A

Figure IIIb.7.3. Free-body diagram of an elemental control volume

Continuity Equation is derived in Example IIIa.3.7 as (1/A)dA/dt + (1/

/dt

+ (dV/dx) = 0. We may now substitute for:

378 IIIb. Fluid Mechanics: Incompressible Viscous Flow

dA/A = dPD/E

gdHD/E

that was derived earlier to couple the continuity equation with the pipe structural

properties. Similarly, d

can be replaced by taking advantage of the definition

of the liquid bulk modulus:

= dP/E

gdH/E

Substituting and rearranging we obtain the relation between the velocity and the

head rise:

),(),(

∂

txV

txdH

IIIb.7.6

where we have also substituted from Equation IIIb.7.5. This is a partial differen-

tial equation in two unknowns. We need one more equation to be able to solve the

set, which is obtained as follows.

Momentum Equation for a one-dimensional flow is derived as (see Exam-

ple IIIa.3.10)

0sin =++

∂

θρτπρ

IIIb.7.7

We may now substitute for pressure, friction, and gravity terms as follows. For

the friction term, we substitute for wall shear stress from Equation IIIb.2.5 or al-

ternatively from the Darcy equation as given by Equation IIIb.3.7 so that:

where A is the flow area. For the gravity force term we notice that sin

∂

(see Figure IIIb.7.3). Finally, we replace the pressure term with the piezometric

head so that:

)H(

∂

−∂

∂

∂ z

where H = P/

(g/g

) + z. Substituting in Equation IIIb.7.7 we obtain;

∂

−

∂

ρρ

Note that by replacing the pressure term with piezometric head, the resulting equa-

tion applies only to liquids. Dividing through by

and canceling the dz/dx terms,

the momentum equation reduces to

7. Fundamentals of Waterhammer Transients 379

∂

IIIb.7.8

Now that we have derived the governing equations, we embark on finding mathe-

matical means of solving Equation IIIb.7.6 and IIIb.7.8.

Solving the Governing Equations. The reason problems involving fast tran-

sients are more complicated, is the fact that we have to solve a set of coupled, non-

linear, partial differential equations,

),(HH

∂

txV

∂

where the first term of Equation IIIb.7.6 is now expanded. To be able to tackle

this set of equations, we first try to eliminate as many nonlinear terms as possible.

Such elimination undoubtedly leads to the introduction of some uncertainties in

the results. However, if the eliminated terms are negligible as compared with

other terms, then the degree of uncertainty will be much less. As was discussed in

Section IIIa.3.2, the non-linearity is due to the convective acceleration term. For-

tunately, V

∆H/∆x in the continuity equation and V∆V/∆x in the momentum equa-

tion are small terms compared with the other terms. That is, the temporal changes

in velocity and the head rise (

∆V/∆t and ∆H/∆t) are much longer than the spatial

changes. Also note that such terms as

∆H/∆x and ∆V/∆x are multiplied by large

values such as g and c

/g, respectively. Dropping the less significant terms, the set

simplifies to:

∂

IIIb.7.9

∂

IIIb.7.10

Despite the above simplification, no general solution to this set of equations exists.

An interesting way to make this set more amenable to a solution is the method of

characteristics, which converts the set of coupled non-linear partial differential

equation into a set of coupled ordinary differential equations. As demonstrated by

Equation IIIa.2.2, total derivative of velocity for example, in one dimension is

found as:

∂

IIIb.7.11

We then note that for V, the space derivative exits in Equation IIIb.7.9 and the

time derivative exists in Equation IIIb.7.10. For H, the time derivative exists in

Equation IIIb.7.9 and the space derivative exists in Equation IIIb.7.10. It then ap-

380 IIIb. Fluid Mechanics: Incompressible Viscous Flow

pears that if these equations are added together, the resulting equation will contain

all the terms that we need for setting up the total derivatives. However, we add

these by multiplying the first equation by an unknown factor

and then add it to

the second equation:

∂

IIIb.7.12

By comparing Equation IIIb.7.12 with Equation IIIb.7.11, we note that if dx/dt =

λc

/g, then the first bracket, for velocity, would have the form of the total deriva-

tive. Similarly, for the second bracket, we need to have dx/dt = g/

λ. We then con-

clude that

λc

/g = g/

. From here, we find

= ± g/c. We also find that dx/dt =

±c. Hence, the governing equations known as the compatibility equations be-

come:

–

) 0

=+−

For c

−=

IIIb.7.14

): 0

=++

For c

IIIb.7.13

Let’s consider the case of the reservoir and the instant closure of a valve, as shown

in Figure IIIb.7.4. We first divide the pipe length into N equally spaced segments

∆x = L/N. In this case N = 4 hence, there are five nodes. Initially liquid is steadily

flowing in the pipe. At time t the valve is instantly closed. Closure of the valve

results in the appearance of a pressure wave, having a magnitude of

∆H ≅ c∆V/g,

as predicted by Equation IIIb.7.1 for V

<< c, traveling upstream. Our goal is to

find V and H for all the nodes along the pipe. The time it takes the disturbance to

reach node 4 is given by

∆t = ∆x/c. The information about velocity and head at

node 4 is related to dx/dt = –c hence, it is predicted by the C

–

equation. The C

equation transmits information in the +c direction. We therefore can find H

and

from similar information at nodes 3 and 5, which are known at time t.

∆Η

12345

t+∆t

Known: V

, H

, and H

Unknow: V

, H

2∆t

∆t

x = L

∆x

i+1

i-1

(a) (b) (c)

Figure IIIb.7.4. Graphical representation of C- and C+ solutions for an instant valve clo-

sur

7. Fundamentals of Waterhammer Transients 381

Period of Pressure Pulse. Let’s now find the time it takes for the wave to

travel back and forth from the valve to the tank and returning to the valve. Con-

sider the tank of Figure IIIb.7.5. Water is steadily flowing from the tank in the

pipe. We then suddenly close the valve and examine the system response to the

valve closure. To simplify the discussion, we make the following three assump-

tions:

− the connecting pipe is frictionless. This assumption eliminates the considera-

tion of damping.

− water level in the tank is constant (pressure head is h

from the pipe centerline)

prior to the closure of the valve. This assumption implies steady flow of water

in the pipe.

− the magnitude of the negative pressure pulse is such that the absolute pressure

remains higher than water vapor pressure. This assumption eliminates the con-

sideration of liquid flashing to vapor.

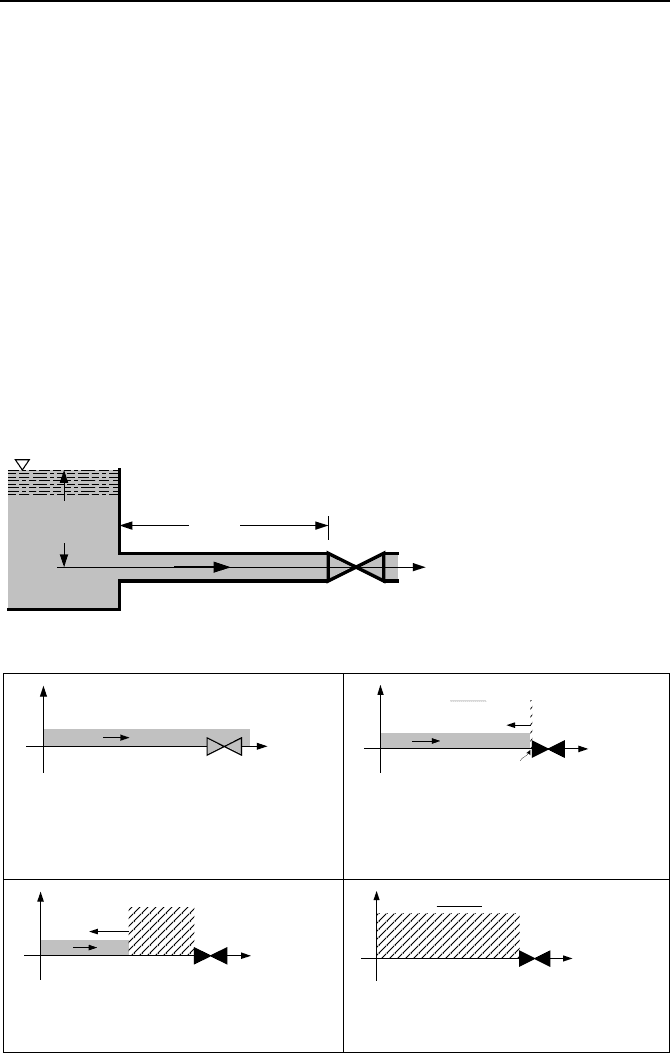
As shown in Figure IIIb.7.5, the period for the pressure pulse to complete a cycle,

in a frictionless pipe of length L, is 4L/c.

head

A- The valve is fully open. Water is flow-

ing under steady state condition in the fric-

tionless pipe, having a pressure head of h

and velocity of V

= (2gh

)

1/2

head

∆h=cV

V = 0

t = 0

B- At time zero, due to sudden valve clo-

sure, the head rises to cV

/g and the dis-

turbance travels back towards the tank,

while water is still flowing in the pipe to-

wards the valve

head

V = 0

C- As the wave front progresses towards the

tank, more fluid becomes stagnant and more

velocity head changes to pressure head.

head

V = 0

t = L/c

D- At time L/c, pressure wave finally

reaches the tank and flow in the entire pipe

becomes stagnant.