Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


The dynamic permeability measures fluid transport in a porous medium under
dynamic wave excitation. It is given by (Johnson et al., 1987)
oðÞ¼
0
1 4i
2
2
0
pf
o=
2
2
ðÞ
1=2
it
0
pf
o=ðÞ
where
0
is the static Darcy permeability, t is tortuosity, L is a measure of the pore
size given approximately by
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
8
0
=
p
.
In the low-frequency limit the dynamic permeability goes to the static Darcy
permeability, while in the high-frequency limit
oðÞ!i= t
pf
o
After finding the roots of the dispersion equation numerically, the Stoneley wave
phase velocity and attenuation are given by
V
stoneley
¼ o =ReðkÞ
Q
1
stoneley
¼ 2ImðkÞ=ReðkÞ
Tang et al. (1991) present a simplified Biot–Rosenbaum model by decoupling the
elastic and flow effects in the full Biot–Rosenbaum model. This reduces the com-
plexity of root finding to an approximate analytical expression for the Stoneley phase
wavenumber k:
k ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
k
2
e
þ
2i
pf
oðoÞR
R
2
a
2
ðÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D þ k
2
e
q
K
1
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D þ k
2
e
p
K
0
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D þ k
2
e
p
v
u
u
t
D ¼
oðÞK
pf
=ðÞ
1 þ
K
pf
lþ2ðÞ
1 þ
4=3K
dry
lþ2ðÞ
K
m
hi
a ¼ tool radius
where D is the diffusivity modified to correct for the elasticity of the medium, and K
0
and K
1
are modified Bessel functions of the second kind. The parameter k
e
in the
above expression is the elastic Stoneley wavenumber, which can be estimated from
the density and effective elastic moduli (or P- and S-wave velocities) of the equiva-
lent formation (Tang and Cheng, 2004). The tool radius a can be set to 0 to model a
fluid-filled borehole without a tool. A low-frequency approximation to the Stoneley
wave slowness (assuming a ¼ 0) is given by (Tang and Cheng, 2004)
S
2
¼
pf
K
pf
þ
pf
þ
2i
pf
0
oR
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D
p
K
1
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D
p
K
0
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D
p
2
4
3
5
167 3.16 Waves in boreholes

The first term is the elastic component while the second term represents the effect of
formation permeability and fluid flow. The second term is usually small compared
with the first term. Therefore it is difficult to estimate formation permeability using
this expression for Stoneley wave slowness.
The Stoneley wavenumber k obtained from the simplified theory matches very well
the exact wavenumber for fast formations. For slow formations, a better match is
obtained by applying an empirical correction to account for borehole compliance.
With the empirical correction, the expression for the Stoneley wavenumber is (Tang
and Cheng, 2004)
k ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
k
2
e
þ
2i
pf
oðoÞR
R
2
a
2
ðÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D þ k
2
e
q
1 þ B
K
1
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D þ k
2
e
p
K
0
R
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=D þ k
2
e
p
v
u
u
t
B ¼ f
e
R
I
1
f
e
RðÞ
I
0
f
e
RðÞ
f
e
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
k
2
e
k
2
f
p
¼ the radial wavenumber for an equivalent elastic formation
k
f
¼ o =
f
¼ the acoustic wavenumber in the borehole fluid
¼ V
S
=
f
¼ the ratio of the formation S-wave velocity to the acoustic velocity in the
borehole fluid.
Uses
The results described in this section can be used to model wave propagation and
geometric dispersion in boreholes.
Assumptions and limitations
The results described in this section assume the following:
isotropic or TI, linear, homogeneous, elastic or poroelastic formation;
a borehole of circular cross-section;
for the TI dispersion relation, the borehole axis is along the symmetry axis; and
open-hole boundary conditions at the borehole interface.
Extensions
The Biot–Rosenbaum theory has been extended to anisotropic poroelastic formations
with multipole excitations (Schmitt, 1989).
168 Seismic wave propagation

4
Effective elastic media: bounds
and mixing laws
4.1 Hashin–Shtrikman–Walpole bounds
Synopsis
If we wish to predict the effective elastic moduli of a mixture of grains and pores
theoretically, we generally need to specify: (1) the volume fractions of the various
phases, (2) the elastic moduli of the various phases, and (3) the geometric details of
how the phases are arranged relative to each other. If we specify only the volume
fractions and the constituent moduli, the best we can do is to predict the upper and
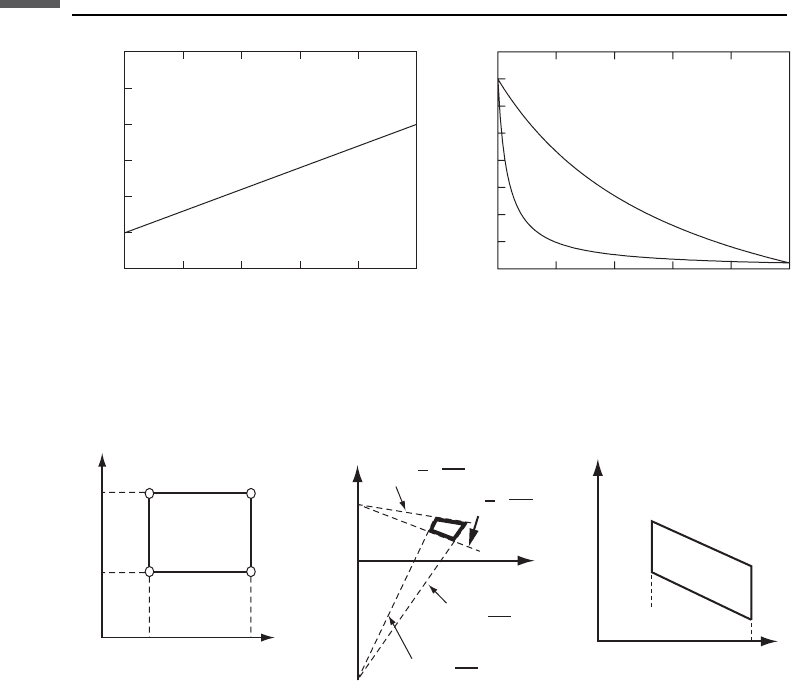
lower bounds (shown schematically in Figure 4.1.1).
At any given volume fraction of constituents the effective modulus will fall
between the bounds (somewhere along the vertical dashed line in the plot of bulk
modulus, Figure 4.1.1), but its precise value depends on the geometric details. We
use, for example, terms like “stiff pore shapes” and “soft pore shapes.” Stiffer shapes
cause the value to be higher within the allowable range; softer shapes cause the value
to be lower. The best bounds for an isotropic linear elastic composite, defined as
giving the narrowest possible range without specifying anything about the geometries
of the constituents, are the Hashin–Shtrikman bounds (Hashin and Shtrikman, 1963).
When there are only two constituents, the bounds are written as
K
HS
¼ K
1
þ
f
2
ðK
2
K
1
Þ
1
þ f
1
ðK
1
þ
4
3
m
1
Þ
1
ð4:1:1Þ
m
HS
¼ m
1
þ
f
2
ðm
2
m
1
Þ
1
þ 2f
1
ðK
1
þ 2m
1
Þ=½5m
1
ðK
1
þ
4
3
m
1
Þ
ð4:1:2Þ
where K
1
and K
2
are the bulk moduli of individual phases; m
1
and m
2
are the shear moduli
of individual phases; and f
1
and f
2
are the volume fractions of individual phases.
With equations (4.1.1) and (4.1.2), upper and lower bounds are computed by
interchanging which material is termed 1 and which is termed 2. The expressions
yield the upper bound when the stiffest material is termed 1 and the lower bound
when the softest material is termed 1. Use of the above equations assumes that the
constituent with the larger bulk modulus also has the larger shear modulus and the
169

constituent with the smaller bulk modulus also has the smaller shear modulus.
Slightly more general forms, sometimes called the Walpole ( 1966) bounds or the
Hashin–Shtrikman–Walpole bounds, can be written as
K
HS
¼ K
1
þ
f
2
ðK
2
K
1
Þ
1
þ f
1
ðK
1
þ
4
3
m
m
Þ
1
ð4:1:3Þ
m
HS
¼ m
1
þ
f
2
ðm
2
m
1
Þ
1
þ f
1
m
1
þ
m
m
6
9K
m
þ 8m
m
K
m
þ 2m
m
1
ð4:1:4Þ
where the subscripts 1 and 2 again refer to the properties of the two components.
Equations (4.1.3) and (4.1.4) yield the upper bound when K
m
and m
m
are the
maximum bulk and shear moduli of the individual constituents, and the lower bound
when K
m
and m
m
are the minimum bulk and shear moduli of the constituents. The
maximum (minimum) shear modulus might come from a different constituent from the
maximum (minimum) bulk modulus. This would be the case, for example, for a mixture
of calcite K ¼ 71; m ¼ 30 GPaðÞand quartz K ¼ 37; m ¼ 45 GPaðÞ: Equation (4.1.4)
reduces to equation (4.1.2) when one constituent has both the maximum bulk and shear
moduli, while the other constituent has the minimum bulk and shear moduli.
The physical interpretation of the Hashin–Shtrikman bounds for bulk modulus is
shown schematically in Figure 4.1.2. The space is filled by an assembly of spheres of
material 2, each surrounded by a shell of material 1. Each sphere and its shell have
precisely the volume fractions f
1
and f
2
. The upper bound is realized when the stiffer
material forms the shell; the lower bound is realized when it is in the core. The
physical interpretation implies a very wide distribution of sizes of the coated spheres
such that they fill all the space.
A more general form of the Hashin–Shtrikman–Walpole bounds, which can be
applied to mixtures of more than two phases (Berryman, 1995), can be written as
K
HSþ
¼ ðm
max
Þ;
m
HSþ
¼ ðzðK
max
; m
max
ÞÞ;
K
HS
¼ ðm
min
Þ
m
HS
¼ ðzðK
min
; m
min
ÞÞ
Volume fraction of material 2
Effective bulk modulus
K
2
K
1
Upper bound
Lower bound
Stiffer
Softer
Volume fraction of material 2
Effective shear modulus
m
1
m
2
Upper bound
Lower bound
Figure 4.1.1 Schematic representation of the upper and lower bounds on the elastic bulk
and shear moduli.
170 Effective elastic media: bounds and mixing laws

where
ðzÞ¼
1
KðrÞþ
4
3
z
*+
1
4
3
z
ðzÞ¼
1
mðrÞþz
1
z
zðK; mÞ¼
m
6
9K þ 8m
K þ 2m
The brackets hiindicate an average over the medium, which is the same as an
average over the constituents weighted by their volume fractions.
Compute the Hashin–Shtrikman upper and lower bounds on the bulk and shear
moduli for a mixture of quartz, calcite, and water. The porosity (water fraction) is
27%, quartz is 80% by volume of the solid fraction, and calcite is 20% by volume
of the solid fraction. The moduli of the individual constituents are:
K
quartz
¼ 36 GPa K
calcite
¼ 75 GPa K
water
¼ 2:2 GPa;
m
quartz
¼ 45 GPa m
calcite
¼ 31 GPa m
water
¼ 0 GPa
Hence
m
min
¼ 0 GPa; m
max
¼ 45 GPa; K
min
¼ 2:2 GPa; and K
max
¼ 75 GPa
K
HS
¼ ðm
min
Þ
¼
2:2
þ
ð1 Þð0:8Þ
36:0
þ
ð1 Þð0:2Þ
75:0
1
¼ 7:10 GPa
Figure 4.1.2 Physical interpretation of the Hashin–Shtrikman bounds for the bulk
modulus of a two-phase material.
171 4.1 Hashin–Shtrikman–Walpole bounds

K
HSþ
¼ ðm
max
Þ
¼
2:2 þ
4
3
45
þ
ð1 Þð0:8Þ
36:0 þ
4
3
45
þ
ð1 Þð0:2Þ
75:0 þ
4
3
45:0
"#
1
4
3
45
¼ 26:9 GPa
zðK
max
; m
max
Þ¼
45
6
9 75 þ 8 45
75 þ 2 45
¼ 47:0 GPa
zðK
min
; m
min
Þ¼0 GPa
m
HSþ
¼ ðzðK
max
; m
max
ÞÞ
¼
47:0
þ
ð1 Þð0:8Þ
45:0 þ 47:0
þ
ð1 Þð0:2Þ
31:0 þ 47:0
1
47:0
¼ 24:6 GPa
m
HS
¼ ðzðK
min
; m
min
ÞÞ
¼ 0
The separation between the upper and lower bounds depends on how different the
constituents are. As shown in Figure 4.1.3, the bounds are often quite similar when
mixing solids, for the moduli of common minerals are usually within a factor of 2 of
each other. Because many effective-medium models (e.g., Biot, Gassmann, Kuster–
Tokso
¨
z, etc.) assume a homogeneous mineral modulus, it is often useful (and
adequate) to represent a mixed mineralogy with an “average mineral” equal to either
one of the bounds or to their average (M
HSþ
þM
HS–
)/2. On the other hand, when the
constituents are quite different (such as minerals and pore fluids), the bounds become
quite separated, and we lose some of the predictive value.
Note that when m
min
¼0, K
HS–
is the same as the Reuss bound. In this case, the
Reuss or Hashin–Shtrikman lower bound exactly describes the moduli of a suspen-
sion of grains in a pore fluid (see Section 4.2 on Voigt–Reuss bounds and also
Section 4.3 on Wood’s relation). These also describe the moduli of a mixture of
fluids or gases, or both.
When all phases have the same shear modulus, m ¼m
min
¼m
max
, the upper and
lower bounds become identical, and we obtain the expression from Hill (1963) for the
effective bulk modulus of a composite with uniform shear modulus (see Section 4.5
on composites with uniform shear modulus).
The Hashin–Shtrikman bounds are computed for the bulk and shear moduli. When
bounds on other isotropic elastic constants are needed, the correct procedure is to
172 Effective elastic media: bounds and mixing laws
compute the bounds for bulk and shear moduli and then compute the other elastic
constants from these. Figure 4.1.4 shows schematically the bounds in the planes
(K, m), (n, E), and (l, m). In each case, the allowed pairs of elastic constants lie within
the polygons. Notice how the upper and lower bounds for (K, m ) are uncoupled, i.e.,
any value K
K K
þ
can exist with any value m
m m
þ
. In contrast, the
bounds on n; EðÞboth depend on (K, m) – the upper and lower bounds on n depend on
the value of E, and vice versa. Similarly, the bounds on l are coupled to the value of m.
K and m are more “orthogonal” than l and m.
Uses
The bounds described in this section can be used for the following:
to compute the estimated range of average mineral modulus for a mixture of
mineral grains;
to compute the upper and lower bounds for a mixture of mineral and pore fluid.
68
70
72
74
76
78
80
0 0.2 0.4 0.6 0.8 1
Calcite + Dolomite
Bulk modulus (GPa)
Fraction of dolomite
Upper
bound
Lower
bound
0
10
20
30
40
50
60
70
80
0 0.2 0.4 0.6 0.8 1
Calcite + Water
Bulk modulus (GPa)
Porosity
Upper
bound
Lower
bound
Figure 4.1.3 Hashin–Shtrikman bounds for similar constituents (left) and dissimilar
constituents (right).
E
K
+
n
+
, l
+
n
–
, l
–
λ
ν
E
–
E
+
0.5
0
–1
m
–
m
+
m
–
m
+
K
–
n =
1
2
E
6K
+
–
l = K
+
–2m /3
l = K
–
–2m /3
n =
–1
E
2m
+
+
n =
–1
E
2m
–
+
n =
1
2
E
6K
–
–
Figure 4.1.4 Schematic representation of the Hashin–Shtrikman bounds in the ( K, m), (n,E)
and (l, m) planes.
173 4.1 Hashin–Shtrikman–Walpole bounds
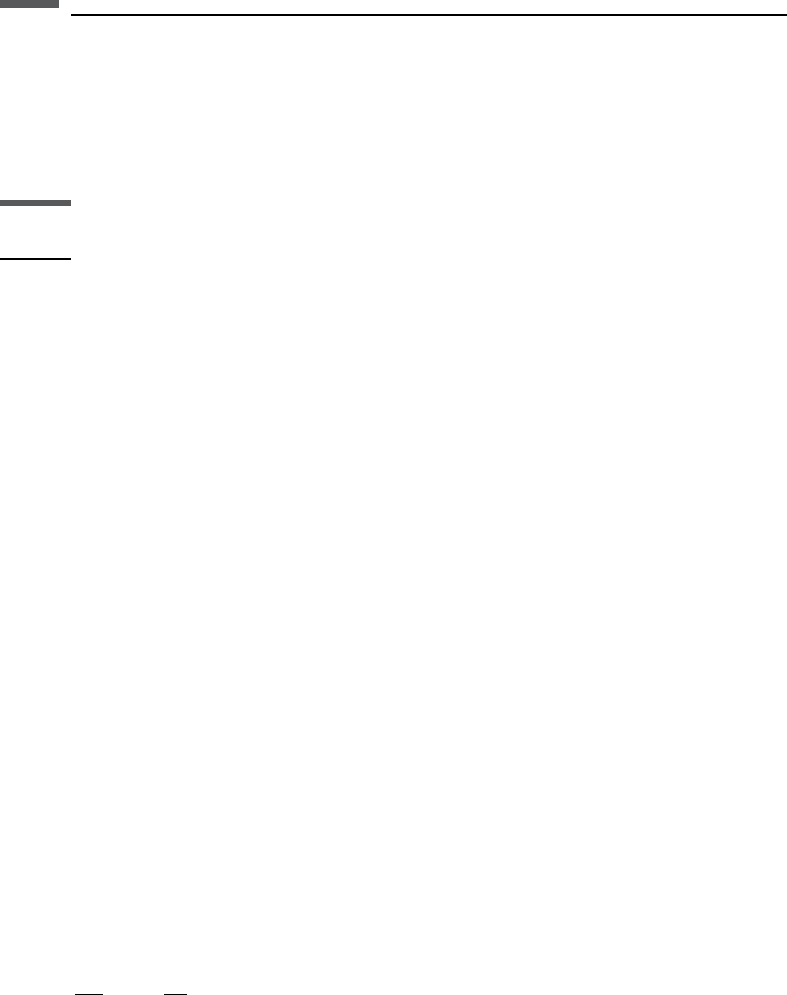
Assumptions and limitations
The bounds described in this section apply under the following conditions:
each constituent is isotropic, linear, and elastic;
the rock is isotropic, linear, and elastic.
4.2 Voigt and Reuss bounds
Synopsis
If we wish to predict theoretically the effective elastic moduli of a mixture of grains
and pores, we generally need to specify: (1) the volume fractions of the various
phases, (2) the elastic moduli of the various phases, and (3) the geometric details of
how the phases are arranged relative to each other. If we specify only the volume
fractions and the constituent moduli, the best we can do is to predict the upper and
lower bounds (shown schematically in Figure 4.2.1).
At any given volume fraction of constituents, the effective modulus will fall
between the bounds (somewhere along the vertical dashed line in Figure 4.2.1), but
its precise value depends on the geometric details. We use, for example, terms like
“stiff pore shapes” and “soft pore shapes.” Stiffer shapes cause the value to be higher
within the allowable range; softer shapes cause the value to be lower. The simplest,
but not necessarily the best, bounds are the Voigt and Reuss bounds. (See also Section
4.1 on Hashin–Shtrikman bounds, which are narrower.)
The Voigt upper bound of the effective elastic modulus, M
V
,ofN phases is
M
V
¼
X
N
i¼1
f
i
M
i
where f
i
is the volume fraction of the ith phase and M
i
is the elastic modulus of the ith
phase. The Voigt bound is sometimes called the isostrain average because it gives
the ratio of the average stress to the average strain when all constituents are assumed
to have the same strain.
The Reuss lower bound of the effective elastic modulus, M
R
, is (Reuss, 1929)
1
M
R
¼
X
N
i¼1
f
i
M
i
The Reuss bound is sometimes called the isostress average because it gives the ratio
of the average stress to the average strain when all constituents are assumed to have
the same stress.
When one of the constituents is a liquid or a gas with zero shear modulus, the
Reuss average bulk and shear moduli for the composite are exactly the same as given
by the Hashin–Shtrikman lower bound.
174 Effective elastic media: bounds and mixing laws

The Reuss average exactly describes the effective moduli of a suspension of solid
grains in a fluid. It also describes the moduli of “shattered” materials in which solid
fragments are completely surrounded by the pore fluid.
When all constituents are gases or liquids, or both, with zero shear moduli, the
Reuss average gives the effective moduli of the mixture exactly.
In contrast to the Reuss average, which describes a number of real physical
systems, real isotropic mixtures can never be as stiff as the Voigt bound (except for
the single phase end-members).
Mathematically M in the Reuss average formula can represent any modulus:
K, m,E, and so forth. However, it makes most sense to compute only the Reuss averages
of the shear modulus, M ¼m, and the bulk modulus, M ¼K, and then compute the
other moduli from these.
Uses
The methods described in this section can be used for the following purposes:
to compute the estimated range of the average mineral modulus for a mixture of
mineral grains;
to compute the upper and lower bounds for a mixture of mineral and pore fluid.
Assumptions and limitations
The methods described in this section presuppose that each constituent is isotropic,
linear, and elastic.
4.3 Wood’s formula
Synopsis
In a fluid suspension or fluid mixture, where the heterogeneities are small compared
with a wavelength, the sound velocity is given exactly by Wood’s (1955) relation
Volume fraction of material 2
Effective bulk modulus
K
1
K
2
Upper bound
Lower bound
Stiffer
Softer
Figure 4.2.1 Effect of changing the volume fraction of constituent materials. The bulk modulus
will move along the vertical dotted line between the two bounds.
175 4.3 Wood’s formula

V ¼
ffiffiffiffiffiffi
K
R
s
where K
R
is the Reuss (isostress) average of the composite
1
K
R
¼
X
N
i¼1
f
i
K
i
and r is the average density defined by
¼
X
N
i¼1
f
i
i
f
i
, K
i
,andr
i
are the volume fraction, bulk moduli, and densities of the phases, respectively.
Use Wood’s relation to estimate the speed of sound in a water-saturated sus-
pension of quartz particles at atmospheric conditions. The quartz properties are
K
quartz
¼36 GPa and r
quartz
¼2.65 g/cm
3
. The water properties are K
water
¼2.2 GPa
and r
water
¼1.0 g/cm
3
. The porosity is f¼ 0.40.
The Reuss average bulk modulus of the suspension is given by
K
Reuss
¼
K
water
þ
1
K
quartz
1
¼
0:4
2:2
þ
0:6
36
1
¼ 5:04 GPa
The density of the suspension is
¼
water
þð1 Þ
quartz
¼ 0:4 1:0 þ 0:6 2:65 ¼ 1:99 g=cm
3
This gives a sound speed of
V ¼
ffiffiffiffiffiffiffiffiffi
K=
p
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
5:04=1:99
p
¼ 1:59 km=s
Use Wood’s relation to estimate the speed of sound in a suspension of quartz
particles in water with 50% saturation of air at atmospheric conditions. The quartz
properties are K
quartz
¼36 GPa and r
quartz
¼2.65 g/cm
3
. The water properties are
K
water
¼2.2 GPa and r
water
¼1.0 g/cm
3
. The air properties are K
air
¼0.000131 GPa
and r
air
¼0.00119 g/cm
3
.Theporosityisf ¼0.40.
The Reuss average bulk modulus of the suspension is given by
K
Reuss
¼
0:5
K
water
þ
0:5
K
air
þ
1
K
quartz
1
¼
0:5 0:4
2:2
þ
0:5 0:4
0:000 131
þ
0:6
36
1
¼ 0:000 65 GPa
176 Effective elastic media: bounds and mixing laws
