Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


cementation only and by adopting certain schemes of cement deposition, we can
relate the parameter a to the current porosity of cemented sand f. For example, we
can use Scheme 1 (see Figure 5.4.3 below), in which all cement is deposited at grain
contacts, to obtain the formula
a ¼ 2
0
3Cð1
0
Þ
1=4
¼ 2
S
0
3Cð1
0
Þ
1=4
or we can use Scheme 2, in which cement is evenly deposited on the grain surface:
a ¼
2ð
0
Þ
3ð1
0
Þ
1=2
¼
2S
0
3ð1
0
Þ
1=2
In these formulas, S is the cement saturation of the pore space. It is the fraction of the
pore space (of the uncemented sand) occupied by cement (in the cemented sand).
If the properties of the cement are identical to those of the grains, the cementation
theory gives results that are very close to those of the Digby model. The cementation
theory allows one to diagnose a rock by determining what type of cement prevails.
For example, the theory helps to distinguish between quartz and clay cement
(Figure 5.4.4). Generally, the model predicts V
P
much more reliably than V
S
.
Grain
Contact
cement
Noncontact
cement
(a) (b) (c)
Scheme 1
Scheme 2
Figure 5.4.3 (a) Schematic representation of types of cement deposition. (b) All cement
deposited at grain contacts. (c) Cement deposited in uniform layer around grains.
Clay-cemented
Quartz-
cemented
2.75
2.50
2.25
2.00
1.75
0.15 0.2 0.25 0.3 0.35
V
S
(km/s)
Theoretical
Curves
Porosity
Clay-cemented
Quartz-cemented
Theoretical
Curves
4.5
4.0
3.5
3.0
2.5
0.15 0.2 0.25 0.3 0.35
V
P
(km/s)
Porosity
Figure 5.4.4 Predictions of V
P
and V
S
using the Scheme 2 model for quartz and clay cement,
compared with data from quartz- and clay-cemented rocks from the North Sea.
257 5.4 Random spherical grain packings

The uncemented (soft) sand model
The uncemented-sand (or “soft-sand”) model allows one to calculate the bulk and
shear moduli of dry sand in which cement is deposited away from grain contacts.Itis
assumed that the starting framework of uncemented sand is a dense random pack of
identical spherical grains with porosity f
0
about 0.36 and average number of contacts
per grain C ¼5 to 9. At this porosity, the contact Hertz–Mindlin theory gives
the following expressions for the effective bulk (K
HM
) and shear (m
HM
) moduli of
a dry, dense, random pack of identical spherical grains subject to a hydrostatic
pressure P:
K
HM
¼
C
2
ð1
0
Þ
2
m
2
18p
2
ð1 nÞ
2
P
"#
1=3
m
HM
¼
5 4n
5ð2 n Þ
3C
2
ð1
0
Þ
2
m
2
2p
2
ð1 nÞ
2
P
"#
1=3
where v is the grain Poisson ratio and m is the grain shear modulus. A version of the
same model allows a fraction f of grain contacts to have perfect adhesion and the rest
to be frictionless; it uses
m
HM
¼
2 þ 3f nð1 þ 3f Þ
5ð2 nÞ
3C
2
ð1 Þ
2
m
2
2p
2
ð1 nÞ
2
P
"#
1=3
To find the effective moduli (K
eff
and m
eff
) at a different porosity f, a heuristic
modified Hashin–Shtrikman lower bound is used:
K
eff
¼
=
0
K
HM
þ
4
3
m
HM
þ
1 =
0
K þ
4
3
m
HM
"#
1
4
3
m
HM
m
eff
¼
=
0
m
HM
þ
m
HM
6
9K
HM
þ8m
HM
K
HM
þ2m
HM
þ
1 =
0
m þ
m
HM
6
9K
HM
þ8m
HM
K
HM
þ2m
HM
2
4
3
5
1
m
HM
6
9K
HM
þ 8m
HM
K
HM
þ 2m
HM
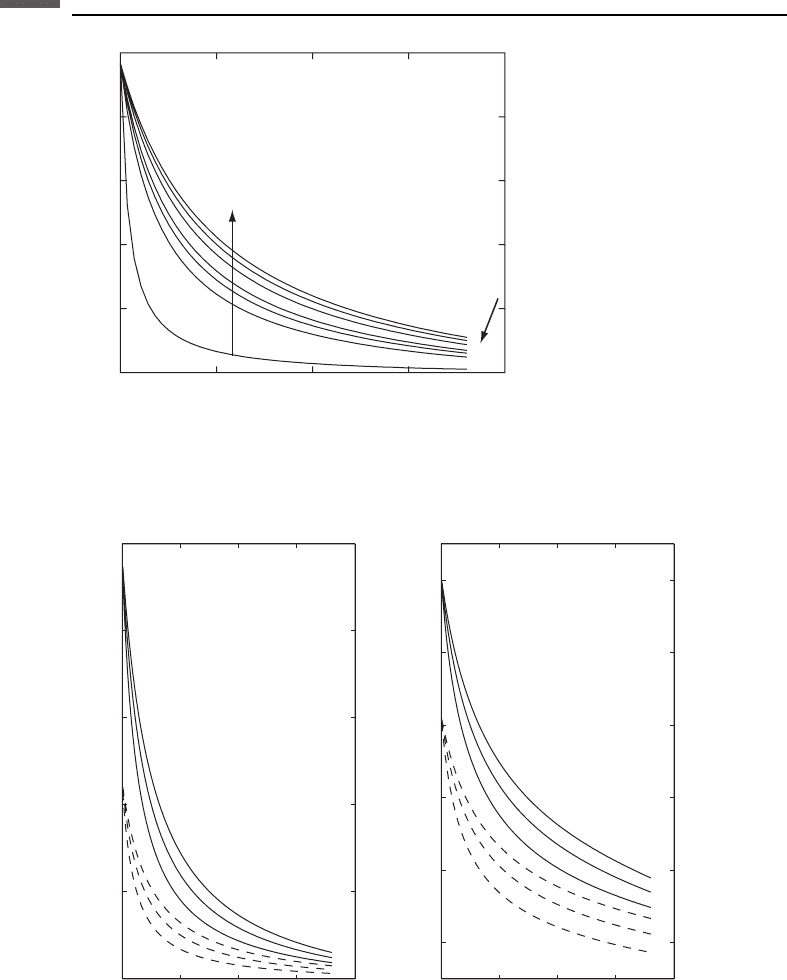
where K is the grain bulk modulus. Figure 5.4.5 shows the curves from this model in
terms of the P-wave modulus, M ¼ K þ
4
3
m. Figure 5.4.6 illustrates the effect of the
parameter f (the fraction of the perfect-adhesion contacts) on the elastic moduli and
velocity in a dry pack of identical quartz grains.
258 Granular media
0
20
40
60
80
100
0 0.1 0.2 0.3 0.4
M-modulus (GPa)
Porosity
Solid
Hertz–
Mindlin
Increasing
pressure
M = rV
2
p
Figure 5.4.5 Illustration of the modified lower Hashin–Shtrikman bound for various effective
pressures. The pressure dependence follows from the Hertz–Mindlin theory incorporated into the
right end-member. All grain contacts have perfect adhesion. The grains are pure quartz.
0 0.1 0.2 0.3 0.4
0
20
40
60
80
100
Porosity
Modulus (GPa)
S
P
0 0.1 0.2 0.3 0.4
1
2
3
4
5
6
Porosity
Velocity (km/s)
S
P
Figure 5.4.6 Illustration of the modified lower Hashin–Shtrikman bound for a varying fractions
of contact with perfect adhesion. The grains are pure quartz and the pack is dry. The effective
pressure is 20 MPa and the critical porosity is 0.36. Left: shear and compressional modulus versus
porosity. Right: V
P
and V
S
versus porosity. Solid curves are for the P-wave velocity and modulus,
while dashed lines are for the S-wave velocity and modulus. For each computed parameter
(modulus and velocity) the upper curves are for perfect adhesion while the lower curves are
for perfect slip. The curve in between is for f ¼ 0.5.
259 5.4 Random spherical grain packings

Calculate V
P
and V
S
in uncemented dry quartz sand of porosity 0.3, at 40 MPa
overburden and 20 MPa pore pressure. Use the uncemented sand model. For pure
quartz, m ¼45 GPa, K ¼36.6 GPa, and v ¼0.06. Then, for effective pressure
20 MPa ¼0.02 GPa,
K
HM
¼
9
2
ð1 0:36Þ
2
45
2
18 3:14
2
ð1 0:06Þ
2
0:02
"#
1=3
¼ 2 GPa
m
HM
¼
5 4 0:06
5ð2 0:06Þ
3 9
2
ð1 0:36Þ
2
45
2
2 3:14
2
ð1 0:06Þ
2
0:02
"#
1=3
¼ 3 GPa
Next,
K
eff
¼
0:3=0:36
2 þ
4
3
3
þ
1 0:3=0:36
36:6 þ
4
3
3
!
1
4
3
3 ¼ 3 GPa
m
eff
¼
0:3=0:36
3 þ 2:625
þ
1 0:3=0:36
45 þ 2:625
1
2:625 ¼ 3:97 GPa
Pure quartz density is 2.65 g/cm
3
; then, the density of the sandstone is
2:65 ð1 0:3Þ¼1:855 g=cm
3
The P-wave velocity is
V
P
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 þ
4
3
3:6
1:855
s
¼ 2:05 km=s
and the S-wave velocity is
V
S
¼
ffiffiffiffiffiffiffiffiffiffiffi
3:6
1:855
r
¼ 1:39 km=s
The stiff-sand and intermediate stiff-sand models
A counterpart to the soft-sand model is the “stiff-sand” model, which uses precisely
the same end-members in the porosity–elastic-modulus plane but connects them with
a heuristic modified Hashin–Shtrikman upper bound:
K
eff
¼
=
0
K
HM
þ
4
3
m
þ
1 =
0
K þ
4
3
m
"#
1
4
3
m
260 Granular media

m
eff
¼
=
0
m
HM
þ
m
6
9K þ8m
K þ2m
þ
1 =
0
m þ
m
6
9K þ8m
K þ2m
2
4
3
5
1
m
6
9K þ 8m
K þ 2m
where K
HM
and m
HM
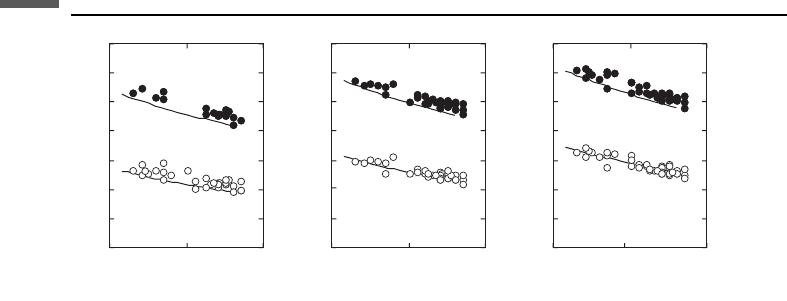
are precisely the same as in the soft-sand model. Figure 5.4.7
compares the elastic moduli and velocity in a dry pack of identical quartz grains as
calculated by the soft- and stiff-sand models. Notice that the stiff-sand model
produces velocity–porosity curves that are essentially identical to those from the
Raymer–Hunt–Gardner empirical model.
The intermediate stiff-sand model uses the functional form of the soft-sand model
(the modified Hashin–Shtrikman lower bound) but with the high-porosity end-point
situated on the stiff-sand model curve. The easiest way to generate such curves is
by simply increasing the coordination number in the soft-sand model (Figure 5.4.7).
This artificially increased coordination number may not be representative of the
actual coordination number of the grain pack at the high-porosity end-point.
0 0.1 0.2 0.3 0.4
0
20
40
60
80
100
Porosity
Modulus (GPa)
P
S
0 0.1 0.2 0.3 0.4
1
2
3
4
5
6
Porosity
Velocity (km/s)
S
P
Raymer–
Hunt–
Gardner
Raymer–
Hunt–
Gardner
Figure 5.4.7 Illustration of the modified lower and upper Hashin–Shtrikman bounds (soft- and stiff-
sand models, respectively). The grains are pure quartz and the pack is dry. The effective pressure is
20 MPa, the coordination number is 9, and the critical porosity is 0.36. Left: shear and
compressional moduli versus porosity. Right: V
P
and V
S
versus porosity. Solid curves are for the
P-wave velocity and modulus while dashed lines are for the S-wave velocity and modulus. The
curves between the two bounds are for the intermediate stiff-sand model that uses the soft-sand
equation with an artificial coordination number of 15.
261 5.4 Random spherical grain packings
These models connect two end-members; one has zero porosity and the modulus of
the solid phase, and the other has high porosity and a pressure-dependent modulus, as
given by the Hertz–Mindlin theory. This contact theory allows one to describe the
noticeable pressure dependence normally observed in sands. Notice that in many
experiments on natural sands and artificial granular packs, the observed dependence
of the elastic moduli on pressure is different from that given by the Hertz–Mindlin
theory. This is because the grains are not perfect spheres, and the contacts have
configurations different from those between perfectly spherical particles.
The high-porosity end-member does not necessarily have to be calculated from the
Hertz–Mindlin theory. The end-member can be measured experimentally on high-
porosity sands from a given reservoir. Then, to estimate the moduli of sands of
different porosities, the modified Hashin–Shtrikman lower bound formulas can be
used, where K
HM
and m
HM
are set at the measured values.
This method provides estimates for velocities in uncemented sands. In Figures 5.4.8
and 5.4.9, the curves are from the theory.
This method can also be used for estimating velocities in sands of porosities
exceeding 0.36.
Caveat on the use of effective medium models for granular media
Granular media have properties lying somewhat between solids and liquids and are
sometimes considered to be a distinct form of matter. Complex behavior arises from
the ability of grains to move relative to each other, modify their packing and coordin-
ation numbers, and rotate. Observed behavior, depending on the stress and strain
conditions, is sometimes approximately nonlinearly elastic, sometimes viscoelastic,
and sometimes somewhat fluid-like. A number of authors (Goddard, 1990; Makse
et al., 1999, 2000, 2004) have shown that this complex behavior causes effective
medium theory to fail in cohesionless granular assemblies. Closed-form effective
1
2
3
0.2 0.3 0.4
Velocity (km/s)
Porosity
V
P
V
S
Saturated
P
eff
= 5 MPa
1
2
3
0.2 0.3 0.4
Porosity
V
P
V
S
Saturated
P
eff
= 15 MPa
1
2
3
0.2 0.3 0.4
Porosity
V
P
V
S
Saturated
P
eff
= 30 MPa
Figure 5.4.8 Prediction of V
P
and V
S
using the modified lower Hashin–Shtrikman bound,
compared with measured velocities from unconsolidated North Sea samples.
262 Granular media

medium theories tend to predict the incorrect (relative to laboratory observations)
dependence of effective moduli on pressure, and poor estimates of the bulk to shear
moduli ratio. Numerical methods, referred to as “molecular dynamics” or “discrete
element modeling,” which simulate the motions and interactions of thousands of
grains, appear to come closer to predicting observed behavior (e.g., Makse et al.,
2004; Garcia and Medina, 2006). Closed-form effective medium models can be
useful, because it is not always practical to run a numerical simulation; however,
model predictions of the types presented in this section must be used with care.
Uses
The methods can be used to model granular high-porosity rocks, as well as rocks in
the entire porosity range, depending on what type of diagenetic transformation
reduced the original high porosity.
Assumptions and limitations
The grain contact models presuppose the following:
the strains are small;
grains are identical, homogeneous, isotropic, elastic spheres;
except for the models for regular packings, packings are assumed to be random and
statistically isotropic; and
the effective elastic constants are relevant for long-wavelength propagation, where
wavelengths are much longer (more than 10 times) compared with the grain radius.
1
1.5
2
2.5
0.3 0.35 0.4 0.45 0.5
Velocity (km/s)
Porosity
V
P
V
S
North Sea
sand
Ottawa
sand
Theory
Figure 5.4.9 Prediction of V
P
and V
S
using the modified lower Hashin–Shtrikman bound,
compared with measured velocities from North Sea and Ottawa sand samples.
263 5.4 Random spherical grain packings

Extensions
To calculate the effective elastic moduli of saturated rocks (and their low-frequency
acoustic velocities), Gassmann’s formula should be applied.
5.5 Ordered spherical grain packings: effective moduli
Synopsis
Ordered packings of identical spherical particles are generally anisotropic; thus their
effective elastic properties can be described through stiffness matrices.
Simple cubic packing
The coordination number is 6, and the porosity is 47%. The stiffness matrix is
C
11
C
12
C
12
000
C
12
C
11
C
12
000
C
12
C
12
C
11
000
000
1
2
ðC
11
C
12
Þ 00
000 0
1
2
ðC
11
C
12
Þ 0
000 0 0
1
2
ðC
11
C
12
Þ
0
B
B
B
B
B
B
@
1
C
C
C
C
C
C
A
where
c
11
¼ c
0
c
12
¼
n
2ð2 n Þ
c
0
c
0
¼
3m
2
P
2ð1 n Þ
2
"#
1=3
P is the hydrostatic pressure, and m and v are the shear modulus and Poisson ratio of
the grain material, respectively.
Hexagonal close packing
The coordination number is 12, and the porosity is about 26%. The stiffness matrix is
C
11
C
12
C
13
000
C
12
C
11
C
13
000
C
13
C
13
C
33
000
000C
44
00
0000C
44
0
00000C
66
0
B
B
B
B
B
B
@
1
C
C
C
C
C
C
A
264 Granular media

where
c
11
¼
1152 1848v þ 725v
2
24ð2 vÞð12 11vÞ
c
0
c
12
¼
vð120 109vÞ
24ð2 vÞð12 11vÞ
c
0
c
13
¼
v
3ð2 vÞ
c
0
c
33
¼
4ð3 2vÞ
3ð2 vÞ
c
0
c
44
¼ c
55
¼
6 5v
3ð2 vÞ
c
0
c
66
¼
576 948v þ 417v
2
24ð2 vÞð12 11vÞ
c
0
Face-centered cubic packing
The coordination number is 12, and the porosity is about 26%. The stiffness matrix is
C
11
C
12
C
12
000
C
12
C
11
C
12
000
C
12
C
12
C
11
000
000C
44
00
0000C
44
0
00000C
44
0
B
B
B
B
B
B
@
1
C
C
C
C
C
C
A
where
c
11
¼ 2c
44
¼
4 3v
2 v
c
0
c
12
¼
v
2ð2 vÞ
c
0
Uses
The results of this section are sometimes used to estimate the elastic properties of
granular materials.
Assumptions and limitations
These models assume identical, elastic, spherical grains under small-strain conditions.
265 5.5 Ordered spherical grain packings

6
Fluid effects on wave propagation
6.1 Biot’s velocity relations
Synopsis
Biot (1956) derived theoretical formulas for predicting the frequency-dependent
velocities of saturated rocks in terms of the dry-rock properties. His formulation
incorporates some, but not all, of the mechanisms of viscous and inertial interaction
between the pore fluid and the mineral matrix of the rock. The low-frequency
limiting veloc ities, V
P0
and V
S0
, are the same as those predicted by Gassmann’s
relations (see the discussion of Gassmann in Section 6.3). The high-frequency
limiting velocities, V
P1
and V
S1
(cast in the notation of Johnson and Plona, 1982),
are given by
V
P1
ðfast; slowÞ¼
½
2
4ð
11
22
2
12
ÞðPR Q
2
Þ
1=2
2
11
22
2
12
()
1=2
V
S1
¼
m
fr
fl
a
1
1=2
¼ P
22
þ R
11
2Q
12
P ¼
ð1 Þð1 K
fr
=K
0
ÞK
0
þ K
0
K
fr
=K
fl
1 K
fr
=K
0
þ K
0
=K
fl
þ
4
3
m
fr
Q ¼
ð1 K
fr
=K
0
ÞK
0
1 K
fr
=K
0
þ K
0
=K
fl
R ¼
2
K
0
1 K
fr
=K
0
þ K
0
=K
fl
11
¼ð1 Þ
0
ð1 aÞ
fl
22
¼ a
fl
266
