Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


curves can be generated (Figure 4.17.4), computed as an upper Hashin–Shtrikman
mix of “frame,” taken from the modified upper bound, and suspension, taken from
the lower Reuss bound. IF is the volume fraction of load-bearing frame and 1 – IF is
the fraction of suspension. The isoframe modulus at each porosity is computed
from the frame and suspension moduli at the same porosity. The calculation is carried
out separately for bulk and shear moduli, from which the P-wave modulus can be
calculated.
The bulk modulus K of an elastic porous medium can be expressed as
1
K
¼
1
K
min
þ
~
K
where
~
K
is the saturated pore-space stiffness (Section 2.9) given by
~
K
¼ K
þ
K
min
K
fluid
K
min
þ K
fluid
and K
f
is the dry-rock pore-space stiffness defined in terms of the pore volume n and
confining stress s
c
:
1
K
¼
1
v
@v
@
c
Figure 4.17.5 shows a plot of bulk modulus versus porosity with contours of constant
K
f
. A large value of K
f
indicates a stiff pore space, while small K
f
indicates a soft
pore space. K
f
¼0 corresponds to a suspension.
0 0.1 0.2 0.3 0.4 0.5 0.6
0
20
40
60
80
100
Porosity
P-wave modulus
Modified upper
Hashin–Shtrikman
Reuss
IF =1
0.8
0.6
0.4
0.2
Critical
porosity
Figure 4.17.4 The isoframe model. The modified upper Hashin–Shtrikman curve is assumed to
describe a strong frame of grains in good contact. The Reuss average curve describes a suspension
of grains in a fluid. Each isoframe curve is a Hashin–Shtrikman mix of a fraction IF of frame
with (1 IF) of suspension.
227 4.17 Bound-filling models

Uses
The bound-filling models described here provide a means to describe the stiffness of
rocks that fall in the range between upper and lower bounds. The modified Hashin–
Shtrikman and modified Voigt averages have been found to be useful depth-trend
lines for sand and chalk sediments. The BAM model provides a heuristic fluid-
substitution strategy that seems to work best at high frequency. The isoframe model
allows one to estimate the moduli of rocks composed of a consolidated grain
framework with inclusions of nonload-bearing grain suspensions.
Assumptions and limitations
These models are based on isotropic linear elasticity. All of the bound-filling models
provided here contain at least some heuristic elements, such as the interpretation of
the modified upper bounds.
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Porosity
K /K
min
Reuss
Hashin–Shtrikman
upper bound
0.2
K
φ
/K
min
= 0.1
0.3
0.4
Figure 4.17.5 Normalized bulk modulus versus pressure showing contours of constant K
f
.
228 Effective elastic media: bounds and mixing laws

5
Granular media
5.1 Packing and sorting of spheres
Synopsis
Spheres are often used as idealized representations of grains in unconsolidated and
poorly consolidated sands. They provide a means of quantifying geometric relations,
such as the porosity and the coordination number, as functions of packing and sorting.
Using spheres also allows an analytical treatment of mechanical grain interactions
under stress.
Packings of identical spheres
Porosity
Packing of identical spheres has been studied most, and comes closest to representing
a very well-sorted sand. Table 5.1.1 lists geometric properties of various packings of
identical spheres (summarized from Cumberland and Crawford, 1987, and Bourbie
´
et al., 1987). The first four rows describe perfectly ordered sphere packs. These are
directly analogous to the atomic arrangements in crystals having the same symmet-
ries, although natural sands will never achieve such order. The last row in Table 5.1.1
is for a random, close packing of identical spheres. (Note that complementary
interpretations are possible, depending on whether the grains or the pores are con-
sidered to be spheres.)
Random packing of spheres has been studied both experimentally and theoretic-
ally. Denton (1957) performed 116 repeated experiments of moderately dense,
random packings of spheres. His results highlight the statistical nature of describing
grain packs (hence the use of the term random packings). He found a mean porosity
of 0.391 with a standard deviation of 0.0016. Cumberland and Crawford (1987) found
that Denton’s porosity distribution over the many realizations could be described well
using a beta distribution, and reasonably well with a normal distribution.
Smith et al. (1929) determined the porosity of random sphere packs experimentally
using several preparation techniques, summarized in Table 5.1.2. They observed that
loose random packings resulting from pouring spheres into a container had a porosity
of ~0.447. Shaking systematically decreased porosity, to a minimum of 0.372. Slight
tamping reduced the porosity further to a random close-packed value of 0.359.
229

Table 5.1.1 Geometric properties of packs of identical spheres.
Packing type
Porosity
(nonspheres)
Solid fraction
(spheres)
Void
ratio
Specific
surface area
a
Number of
contacts per
sphere
Radius of
maximum inscribable
sphere
b,c
Radius of maximum
sphere fitting in narrowest
channels
b,c
Simple cubic 1 – p/6 ¼0.476 p/6 ¼0.524 0.910 p/2R 6 0.732 0.414
Simple
hexagonal
1–4p cos(p/6)/
18 ¼0.395
4p cos(p/6)/
18 ¼0.605
0.654 p=
ffiffiffi
3
p
R 8 0.528 0.414 and 0.155
Tetragonal 1 – p/4.5 ¼0.3019 0.6981 0.432 2p/3R 10
Hexagonal
close pack
0.259 0.741 0.350 p=
ffiffiffi
2
p
R 12 0.225 and 0.414 0.155
Face centered
cubic
0.259 0.741 0.350 p=
ffiffiffi
2
p
R
Dense random
pack
~0.36 ~0.64 ~0.56 ~1.92/R ~9
Notes:
a
Specific surface area, S, is defined as the pore surface area in a sample divided by the total volume of the sample. If the grains are spherical, S ¼3(1 – ’)/R.
b
Expressed in units of the radius of the packed spheres.
c
Note that if the pore space is modeled as a packing of spherical pores, the inscribable spheres always have radius equal to 1.

Table 5.1.2 Experimental data from Smith et al. (1929).
Method of random packing
Total number
of spheres
counted Distribution of contacts per sphere
Mean coordination
number* Porosity
456789101112
Poured into beaker 905 6 78 243 328 200 48 2 0 0 6.87 1.05 0.447
Poured and shaken 906 3 54 173 309 233 118 14 2 0 7.25 1.16 0.440
Poured and shaken 887 0 14 69 182 316 212 87 7 0 8.05 1.17 0.426
Shaken to maximum density 1494 0 14 86 192 233 193 161 226 389 9.57 2.02 0.372
Added in small quantities and
intermittently tamped
1562 1 13 77 245 322 310 208 194 192 9.05 1.78 0.359
Note:
*
Column shows mean 1 standard deviation.

More accurate (Cumberland and Crawford, 1987) experimental values for the
porosity of random close packs of 0.3634 0.008 and 0.3634 0.004 were found
by Scott and Kilgour (1969) and Finney (1970), respectively.
Coordination number
The coordination number of a grain pack is the average number of contacts that
each grain has with surrounding grains. Table 5.1.1 shows that the coordination
numbers for perfect packings of identical spheres range from a low of 6 for a simple
cubic packing, to a high of 12 for hexagonal close packing. Coordination numbers in
random packings have been determined by tediously counting the contacts in experi-
mentally prepared samples (e.g., Smith et al., 1929; Wadsworth, 1960; Bernal and
Mason, 1960). Table 5.1.2 shows results from Smith et al. (1929), after counting more
than 5000 spheres in five different packings. There are several important conclusions.
The coordination number increases with decreasing porosity, both being the result
of tighter packing.
Random packs of identical spheres have coordination numbers ranging from ~6.9
(loose packings) to ~9.1 (tight packings).
The coordination number varies widely throughout each sample, from 4 to 12;
hence, the mean alone does not capture the variability.
Tables 5.1.3–5.1.5 show data illustrating a correlation between coordination number
and porosity. Manegold and von Engelhardt (1933) described theoretically the
arrangements of identical spheres. They chose a criterion of the most regular packing
possible for porosities ranging from 0.2595 to 0.7766. Their results are summarized
in Table 5.1.4. Murphy (1982) also compiled coordination number data from the
literature, summarized in Table 5.1.5.
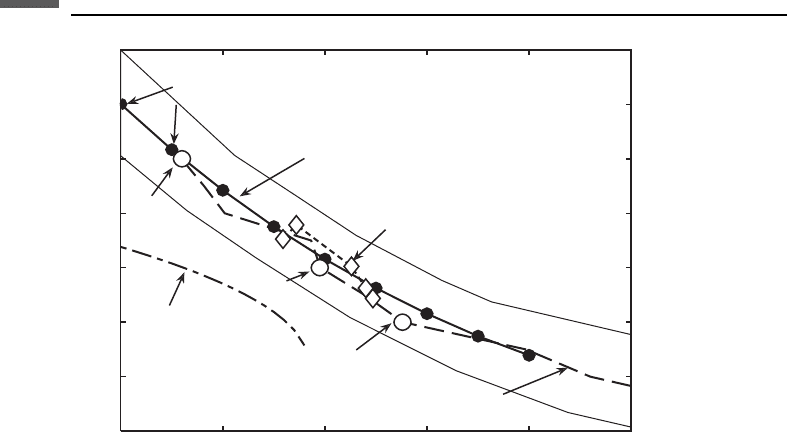
Figure 5.1.1 compares coordination number versus porosity from Smith et al.
(1929), Manegold and von Engelhardt (1933), and Murphy (1982). The data from
various sources are consistent with each other and with the exact values for hexagonal
close packing, simple hexagonal packing, and simple cubic packing. The thin lines
shows the approximate range of one standard deviation of coordination number
observed by Smith et al. (1929). The standard deviation describes the spatial variation
of coordination number throughout the packing, and not the standard deviation of
the mean.
One source of uncertainty in the experimental estimation of coordination number is
the difficulty of distinguishing between actual grain contacts and near-grain contacts.
For the purposes of understanding porosity and transport properties, this distinction
might not be important. However, mechanical and elastic properties in granular
media are determined entirely by load-bearing grain contacts. For this reason, one
might speculate that the equivalent coordination numbers for mechanical applications
might be smaller than those shown in Tables 5.1.1–5.1.5. Wadsworth (1960) argued
that coordination numbers in random packings may be smaller than those discussed
so far, reduced by about 1.
232 Granular media

Table 5.1.4 Data for randomly packed identical spheres
from Manegold and von Engelhardt (1933).
Porosity Coordination number
0.7766 3
0.6599 4
0.5969 5
0.4764 6
0.4388 7
0.3955 8
0.3866 9
0.3019 10
0.2817 11
0.2595 12
Table 5.1.5 Data compiled by Murphy (1982) – not all
identical spheres.
Porosity Coordination number
0.20 14.007
0.25 12.336
0.3 10.843
0.35 9.508
0.40 8.315
0.45 7.252
0.50 6.311
0.55 5.488
0.60 4.783
Table 5.1.3 Data for randomly packed identical spheres
from Smith et al. (1929).
Porosity Coordination number
0.447 6.87 1.05
0.440 7.25 1.16
0.426 8.05 1.17
0.372 9.57 2.02
0.359 9.05 1.78
233 5.1 Packing and sorting of spheres
Garcia and Medina (2006) derived a power-law relation between the coordination
number and the porosity based on fitting data from numerical simulations of granular
media:
C ¼ C
0
þ 9:7
0
ðÞ
0:48
where C
0
¼4.46 and f
0
¼0.384. The relation holds for f f
0
. These relations
between coordination number and porosity can be used in effective medium models
such as those described later in Section 5.4.
Makse et al. (2004) derived a similar relation using numerical simulation of
frictionless spheres:
C ¼ C
0
þ 9:1
0
ðÞ
0:48
where C
0
¼6 and f
0
¼0.37. The Makse et al. relation parallels that of Garcia and
Medina, shifted upward by about 1.5.
Binary mixtures of spheres
Binary mixtures of spheres (i.e., two different sphere sizes) add additional complexity
to random packings. Cumberland and Crawford (1987) review the specific problem
of predicting porosity. Figure 5.1.2 compares theoretical models for porosity
0.2 0.3 0.4 0.5 0.6 0.7
2
4
6
8
10
12
14
16
Porosity
Coordination number
Nonidentical
spheres
Smith et al. (1929)
Murphy (1982)
Manegold and
von Engelhardt (1933)
SC
HCP
SH
Garcia and
Medina (2006)
Figure 5.1.1 Coordination number versus porosity in random sphere packs, from Smith et al.
(1929), Manegold and von Engelhardt (1933), Murphy (1982), and Garcia and Medina ( 2006).
HCP ¼ hexagonal close packed; SH ¼ simple hexagonal; and SC ¼ simple cubic. The thin lines
approximately indicate 1 standard deviation from the data of Smith et al. (1929).
234 Granular media
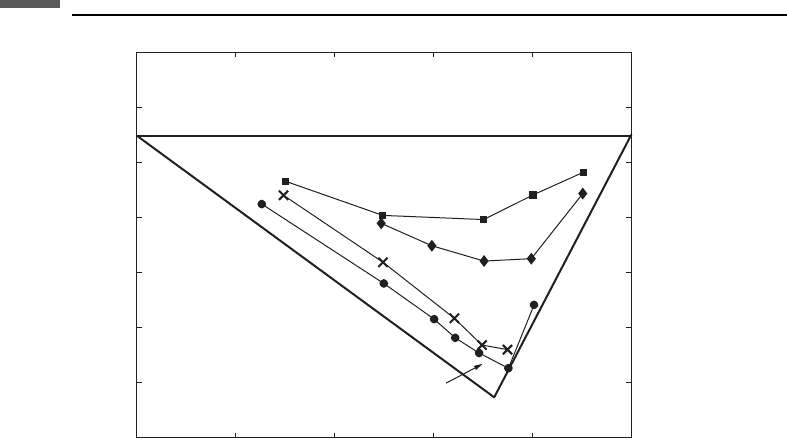
(Cumberland and Crawford, 1987)inanideal binary mixture. The ideal mixture is
composed of two different sphere sizes, where R is the ratio of the large sphere
diameter to the small sphere diameter. The horizontal axis is the volume fraction of
large grains relative to the total solid volume. Point A represents a random close
packing of only small spheres, while point B represents a random packing of only
large spheres. Since A and B each correspond to random packings of identical
spheres, the porosity in each case should be close to 0.36. The lower curves, ACB,
correspond to mixtures where R approaches infinity (practically, R > 30). Moving
from B toward C corresponds to gradually adding small spheres to the pore space of
the large sphere pack, gradually decreasing porosity. The packing of each set of
spheres is assumed to be undisturbed by the presence of the other set (the definition
of an ideal binary mixture). The minimum porosity occurs at point C, where the pore
space of the large sphere pack is completely filled by the smaller sphere pack. The
total porosity at point C is f ¼(0.36)
2
¼0.13 and occurs at a volume fraction of large
grains ~0.73. Moving from A toward C corresponds to gradually adding more large
grains to the packing of small grains. Each solid large grain replaces a spherical
region of the porous small grain packing, hence decreasing porosity. Curve AB
corresponds to R ¼1. In this case, all spheres are identical, so the porosity is always
~0.36. All other ideal binary mixtures should fall within the triangle ABC. Data from
McGeary (1967) for ratios R ¼16, 11.2, 4.8, and 3.5, are plotted and are observed to
lie within the expected bounds. It should be pointed out that McGeary’s experiments
0 20 40 60 80 100
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
Fraction of large grains
Porosity
R = infinity
R = 3.5
R = 4.8
R = 11.2
R =1
A
C
B
R =16
Figure 5.1.2 Porosity in an ideal binary mixture. R is the ratio of the large grain diameter
to the small grain diameter. Curves ABC are bounds; highest porosity occurs when R ¼ 1, and
the lowest occurs when R becomes very large. Data for carefully prepared laboratory binary
mixtures are from McGeary (1967).
235 5.1 Packing and sorting of spheres
were designed to approach an ideal mixture. First, a close random packing of large
spheres was created, and then small particles were added, while keeping a weight on
the packing to minimize disturbing the large grain pack.
The ideal binary mixture model has been used successfully to describe porosities
in mixtures of sand and clay (Marion and Nur, 1991; Marion et al., 1992; Yin, 1992).
Other practical parameters affecting packing
Cumberland and Crawford (1987) list a variety of factors affecting the efficiency of
packing, and consequently the porosity and coordination number.
Energy of deposition. Experiments with spheres indicate that when spheres are
poured (sometimes called pluviated), the packing density increases with the height
of the drop; for many materials, an optimum drop height exists, above and below
which the packing is looser.
Absolute particle size. Experimental evidence suggests that porosity increases with
decreasing absolute particle size. This could result from the increased importance of
surface forces (e.g., friction and adhesion) as the surface-to-volume ratio grows.
Irregular particle shape. Waddell (1932) defined the sphericity c as follows:
¼
S
sphere
S
grain
where S
sphere
is the surface area of a sphere having the same volume as the grain, and
S
grain
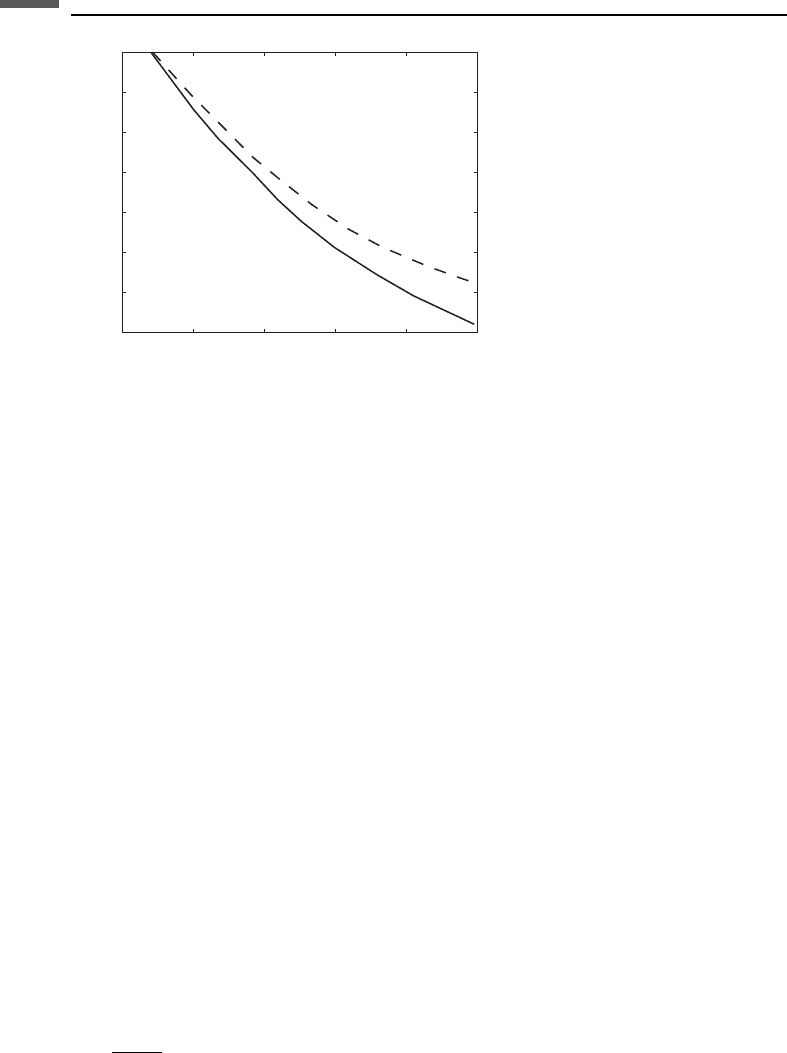
is the actual surface area of the grain. Brown et al. (1966) found experimentally
that deviations from a spherical shape (decreasing sphericity) tend to result in high
porosity, as shown in Figure 5.1.3.
0 0.2 0.4 0.6 0.8 1
0.4
0.5
0.6
0.7
0.8
0.9
1
Sphericity
Porosity
Loose packing
Close packing
Figure 5.1.3 Trends of porosity versus grain sphericity observed by Waddell (1932).
236 Granular media
