Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

8.5 Permeability relations with S

Synopsis

The following family of empirical equations relate permeability to porosity and

irreducible water saturation (Schlumberger, 1991):

the Tixier equation

k ¼ 62500 

the Timur equation

k ¼ 10000

4:5

or k ¼ 8581

4:4

the Coates–Dumanoir equation

k ¼ð90000=m

Þ

where m is the cementation exponent (see Archie’s law, Section 9.4); and the Coates

equation

k ¼ 4900

ð1  S

where the permeability is in milliDarcy and porosity and irreducible water saturation

are unitless volume fractions.

The irreducible water saturation is by definition the lowest water saturation that

can be achieved in a core plug by displacing the water by oil or gas. The state is

usually achieved by flowing oil or gas through a water-saturated sample, or by

spinning the sample in a centrifuge to displace the water with oil or gas. The term

is somewhat imprecise, because the irreducible water saturation is dependent on the

final drive pressure (when flowing oil or gas) or the maximum speed of rotation (in a

centrifuge). The related term, connate water saturation, is the lowest water saturation

found in situ. The smaller the grain size, the larger the irreducible water saturation,

because the capillary forces that retain water are stronger in thinner capillaries.

Figure 8.5.1 compares laboratory permeability data for Fontainebleau sandstone

with permeability calculations according to the above equations. Fontainebleau is

an extremely clean and well-sorted sandstone with large grain size (about 0.25 mm). As

a result, we expect very low irreducible water saturation. This is consistent with Figure

8.5.1, where these data are matched by the curves with S

between 0.05 and 0.10.

Figure 8.5.2 compares permeability calculations according to these equations with the

Kozeny–Carman formula. All equations provide essentially identical results, except for the

Tixier equation, which gives smaller permeability in the low-to-medium porosity range.

Combining the Kozeny–Carman equation for permeability (k

ð  

½1 ð  

Þ

407 8.5 Permeability relations with S

0 0.2 0.4

Permeability (mD)

Porosity

Tixier

Fontainebleau sandstone

0 0.2 0.4

Permeability (mD)

Porosity

Timur

0 0.2 0.4

Permeability (mD)

Porosity

Coates–Dumanoir

m = 2

0 0.2 0.4

Permeability (mD)

Porosity

Coates

Figure 8.5.1 Permeability versus porosity for the Fontainebleau dataset, with theoretical curves

superimposed according to the above equations. The irreducible water saturation varies from

0.05 for the upper curve to 0.50 for the lower curve, with a constant increment of 0.05.

The cementation exponent in the Coates–Dumanoir equation is 2 in this example.

0 0.1 0.2 0.3 0.4

−2

Permeability (mD)

Porosity

Tixier

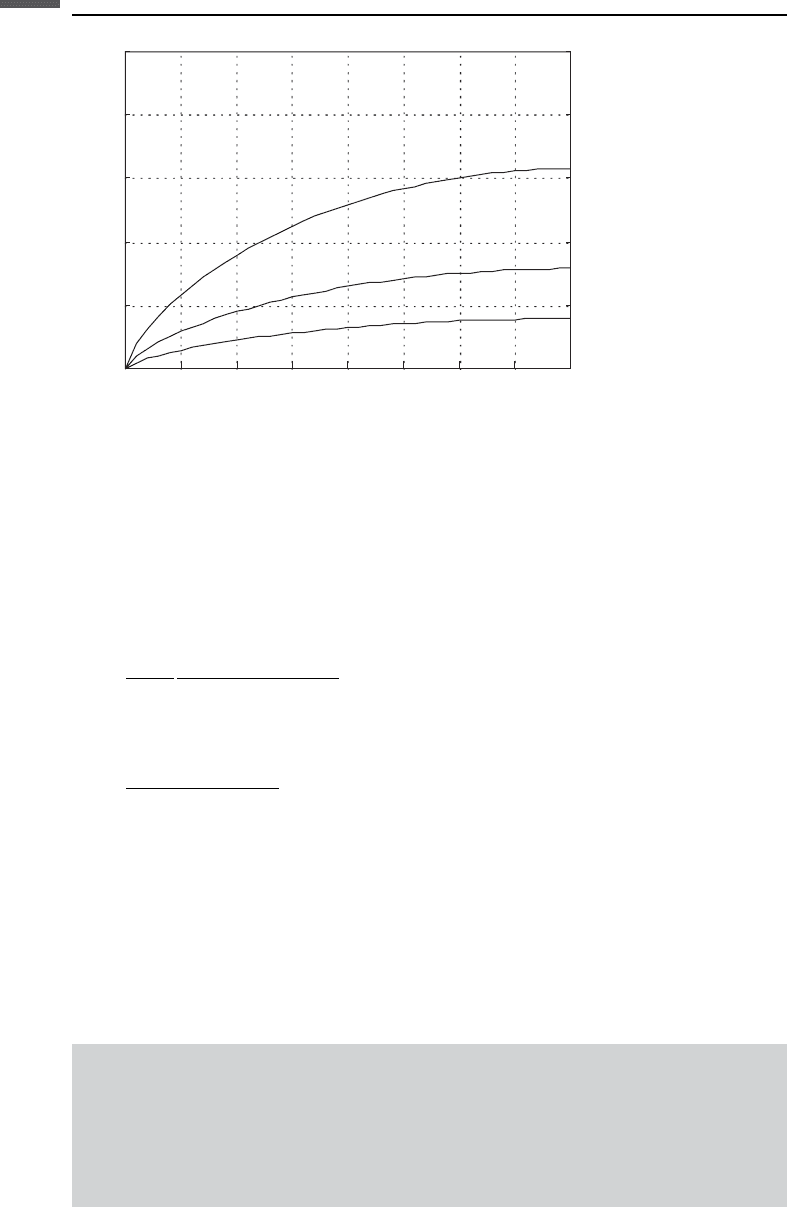
Figure 8.5.2 Permeability versus porosity according to the Tixier equation (bold curve),

Timur, Coates–Dumanoir, and Coates equations (fine curves); and the Kozeny–Carman equation

(open symbols). In these calculations we used a tortuosity of 2.5; an irreducible water saturation

of 0.1; a threshold porosity of 0.02; and a grain size of 0.25 mm.

408 Flow and diffusion

where k

is in mD, d is in mm, and porosity (f and 

) varies from 0 to 1, with the

Timur equation:

TIM

¼ 8581

4:4

yields the following relation between S

and d:

0:025



2:2

½1 ð  

Þt

ð  

1:5

where d is in mm. For 

¼ 0 this equation becomes

0:025

0:7

ð1  Þt

Assume t ¼2. Then the curves of S

versus f according to the last equation are

plotted in Figure 8.5.3.

The result shown in Figure 8.5.3 is somewhat counterintuitive: the irreducible

water saturation increases with increasing porosity. This is due to the fact that in

Timur’s equation, and at fixed permeability, S

increases with increasing f.An

explanation may be that to maintain fixed permeability at increasing porosity, the

pore size needs to reduce, thus resulting in increasing S

Caution

This S

equation is obtained by the ad hoc equating of two different permeability

equations, one of which is based on a crude idealization of the pore-space

geometry, while the other is purely empirical. Therefore, the resulting S

may

deviate from factual experimental values.

0 0.1 0.2 0.3 0.4

0.1

0.2

0.3

0.4

0.5

Porosity

Irreducible water saturation

Figure 8.5.3 Irreducible water saturation versus porosity according to the last equation in the text below.

The curves from top to bottom are for grain sizes of 0.05, 0.1, and 0.2 mm, respectively.

409 8.5 Permeability relations with S

Uses

The permeability relations with irreducible water saturation can be used to estimate

the permeability from this parameter often available from laboratory experiments.

Assumptions and limitations

The following assumptions and limitations apply to the permeability relations with

irreducible water saturation:



these equations are strictly empirical, although they implicitly use the physics-based

relation between the grain size and irreducible water saturation. The functional forms

used in these equations have to be calibrated, whenever possible, to site-specific data;



the rock is isotropic; and



fluid-bearing rock is completely saturated.

8.6 Permeability of fractured formations

Synopsis

Many models for the permeability of fractured formations are based on the expression

for viscous flow rate between two parallel walls:

Q ¼

12

P

where h is the aperture of the fracture, Q is the volume flow rate per unit length

of fracture (normal to the direction of flow),  is the fluid viscosity, and DP is the

pressure drop over length l.

For a set of parallel fractures with spacing D the fracture porosity is

 ¼ h=D

A tortuosity can be defined in the similar way as in the Kozeny–Carman formalism

(Figure 8.4.1) or, through the angle a of the fracture plane to the pressure gradient vector:

t ¼ 1= cos a

Then, using Darcy’s definition of permeability, the permeability of a formation

with parallel fracture planes at angle a relative to the pressure gradient is

k ¼

h

12t

h

cos

If the matrix of the rock (the material between the fractures) has permeability k

then the combined total permeability k

will simply be the sum of the two, the matrix

permeability and the permeability of the fractures:

¼ k

þ k ¼ k

h

cos

410 Flow and diffusion

Since real fracture surfaces are irregular, the simple model for parallel plates must

be modified (see Jaeger et al., 2007, for an excellent summary). A common approach

is to approximate the irregular channel with a smooth parallel channel having an

effective hydraulic aperture h

. It was shown (Beran, 1968) that the hydraulic

aperture is bounded as

3



1

 h



where the operator 

is the average over the plane of the fracture. The lower bound

3



1=3

corresponds to the case where the aperture fluctuates only in the direction

of flow, while the upper bound h



1=3

corresponds to the case where the aperture

varies only in the direction normal to flow.

Renshaw (1995) gave an expression for hydraulic aperture

¼ h

1 þ 

= h

3=2

where 

is the variance of h. Other analyses have been presented by Elrod (1979),

Dagan (1993), and Jaeger et al. (2007).

Uses

The permeability relations for a fractured formation can be used in reservoirs, such as

chalks, carbonates, and shales, where fluid transport is dominated by natural or

artificial fractures.

Assumptions and limitations

The following assumptions and limitations apply to the permeability relations in

fractured formations:



these equations are derived for an idealized pore geometry and thus may fail in an

environment without adequate hydraulic communication between fractures and/or

complex fracture geometry;



fluid-bearing rock is completely saturated.

8.7 Diffusion and filtration: special cases

Synopsis

Nonlinear diffusion

Some rocks, such as coals, exhibit strong sensitivity of permeability (k) and porosity

(f) to net pressure changes. During an injection test in a well, apparent permeability

may be 10–20 times larger than that registered during a production test in the same

well. In this situation, the assumption of constant permeability, which leads to the

411 8.7 Diffusion and filtration: special cases

linear diffusion equation, is not valid. The following nonlinear diffusion equation

must be used (Walls et al., 1991):

ðb

þ b

¼ P þðb

þ gÞðrPÞ

where fluid compressibility b

and pore-volume compressibility b

are defined as



]

; b

where v

is the pore volume and r is the fluid density. The permeability–pressure

parameter g is defined as

g ¼

For one-dimensional plane filtration, the diffusion equation given above is

ðb

þ b

]

þðb

þ gÞ



For one-dimensional radial filtration it is

ðb

þ b

]

þðb

þ gÞ



Hyperbolic equation of filtration (diffusion)

The diffusion equations presented above imply that changes in pore pressure propa-

gate through a reservoir with infinitely high velocity. This artifact results from using

the original Darcy’s law, which states that volumetric fluid flow rate and pressure

gradient are linearly related. In fact, according to Newton’s second law, pressure

gradient (or acting force) should also be proportional to acceleration (time derivative

of the fluid flow rate). This modified Darcy’s law was first used by Biot (1956) in his

theory of dynamic poroelasticity:





t



where t is tortuosity. The latter equation, if used instead of the traditional Darcy’s law,





yields the following hyperbolic equation that governs plane one-dimensional filtration:

]

¼ tðb

þ b

]

ðb

þ b

412 Flow and diffusion

This equation differs from the classical diffusion equation because of the inertia term,

tðb

þ b

]

Changes in pore pressure propagate through a reservoir with a finite velocity, c:

c ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

tðb

þ b

This is the velocity of the slow Biot wave in a very rigid rock.

Uses

The equations presented in this section can be used to calculate fluid filtration and

pore-pressure pulse propagation in rocks.

Assumptions and limitations

The equations presented in this section assume that the fluid is Newtonian and the

flow is isothermal.

413 8.7 Diffusion and filtration: special cases

Electrical properties

9.1 Bounds and effective medium models

Synopsis

If we wish to predict the effective dielectric permittivity e of a mixture of phases

theoretically, we generally need to specify: (1) the volume fractions of the various

phases, (2) the dielectric permittivity of the various phases, and (3) the geometric

details of how the phases are arranged relative to each other. If we specify only the

volume fractions and the constituent dielectric permittivities, then the best we can do

is to predict the upper and lower bounds.

Bounds: The best bounds, defined as giving the narrowest possible range without

specifying anything about the geometries of the constituents, are the Hashin–Shtrikman

(Hashin and Shtrikman, 1962) bounds. For a two-phase composite, the Hashin–Shtrikman

bounds for dielectric permittivity are given by



¼ "

ð"

 "

1

þ f

=ð3"

where e

and e

are the dielectric permittivity of individual phases, and f

and f

are

volume fractions of individual phases.

Upper and lower bounds are computed by interchanging which material is termed 1

and which is termed 2. The expressions give the upper bound when the material with

higher permittivity is termed 1 and the lower bound when the lower permittivity

material is termed 1.

A more general form of the bounds, which can be applied to more than two phases

(Berryman, 1995), can be written as

HSþ

ð"

max

Þ "

HS

ð"

min

ðzÞ¼

"ðrÞþ2z



1

2z

where z is just the argument of the function

ðÞ, and r is the spatial position. The

brackets hiindicate an average over the medium, which is the same as an average

over the constituents weighted by their volume fractions.

414

Spherical inclusions: Estimates of the effective dielectric permittivity, e*, of a

composite may be obtained by using various approximations, both self-consistent

and non-self-consistent. The Clausius–Mossotti formula for a two-component mater-

ial with spherical inclusions of material 2 in a host of material 1 is given by



 "



þ 2"

¼ f

 "

þ 2"

or equivalently



ð"

This non-self-consistent estimate, also known as the Lorentz–Lorenz or Maxwell–

Garnett equation, actually coincides with the Hashin–Shtrikman bounds. The two

bounds are obtained by interchanging the role of spherical inclusions and host material.

The self-consistent (SC) or coherent potential approximation (Bruggeman, 1935;

Landauer, 1952; Berryman, 1995) for the effective dielectric permittivity "



of a

composite made up of spherical inclusions of N phases may be written as

i¼1

 "



þ 2"



¼ 0



ð"



The solution, which is a fixed point of the function

ð"Þ, is obtained by iteration.

In this approximation, all N components are treated symmetrically with no preferred

host material.

In the differential effective medium (DEM) approach (Bruggeman, 1935; Sen et al.,

1981), infinitesimal increments of inclusions are added to the host material until

the desired volume fractions are reached. For a two-component composite with

material 1 as the host containing spherical inclusions of material 2, the effective

dielectric permittivity "



DEM

is obtained by solving the differential equation

ð1  yÞ



DEM

ðyÞ



 "



DEM

ðyÞ

þ 2"



DEM

ðyÞ

½3"



DEM

ðyÞ

where y ¼ f

is the volume fraction of spherical inclusions. The analytic solution with

the initial condition "



DEM

ðy ¼ 0Þ¼"

is (Berryman, 1995)

 "



DEM

ðyÞ

 "





DEM

ðyÞ



1=3

¼ 1  y

The DEM results are path dependent and depend on which material is chosen as the

host. The Hanai–Bruggeman approach (Bruggeman, 1935; Hanai, 1968) starts with

415 9.1 Bounds and effective medium models

the rock as the host into which infinitesimal amounts of spherical inclusions of water

are added. This results in a rock with zero direct current (DC) conductivity because at

each stage the fluid inclusions are isolated and there is no conducting path (usually

the rock mineral itself does not contribute to the DC electrical conductivity). Sen

et al. (1981) in their self-similar model of coated spheres start with water as the initial

host and incrementally add spherical inclusions of mineral material. This leads to a

composite rock with a finite DC conductivity because a conducting path always exists

through the fluid. Both the Hanai–Bruggeman and the Sen et al. formulas are

obtained from the DEM result with the appropriate choice of host and inclusion.

Bounds and estimates for electrical conductivity, s, can be obtained from the

preceding equations by replacing e everywhere with s. This is because the governing

relations for dielectric permittivity and electrical conductivity (and other properties

such as magnetic permeability and thermal conductivity) are mathematically equiva-

lent (Berryman, 1995). The relationship between the dielectric constant, the electrical

field, E, and the displacement field, D, is D ¼ eE. In the absence of charges ▽ · D ¼ 0,

and ▽  E ¼ 0 because the electric field is the gradient of a potential. Similarly, for:



electrical conductivity, s, J ¼ s E from Ohm’s law, where J is the current density,

▽ · J ¼ 0 in the absence of current source and sinks, and ▽  E ¼ 0;



magnetic permeability, m, B ¼ mH, where B is the magnetic induction, H is the

magnetic field, ▽ · B ¼ 0, and in the absence of currents ▽  H ¼ 0; and



thermal conductivity, k, q ¼ –k▽y from Fourier’s law for heat flux q and

temperature y, ▽ · q ¼ 0 when heat is conserved, and ▽  ▽y ¼ 0.

Ellipsoidal inclusions: Estimates for the effective dielectric permittivity of compos-

ites with nonspherical, ellipsoidal inclusions require the use of depolarizing factors

along the principal directions a, b, c of the ellipsoid. The generalization of

the Clausius–Mossotti relation for randomly arranged ellipsoidal inclusions in an

isotropic composite is (Berryman, 1995)



 "



þ 2"

i¼1

ð"

 "

ÞR

and the self-consistent estimate for ellipsoidal inclusions in an isotropic composite is

(Berryman, 1995)

i¼1

ð"

 "



ÞR

i

¼ 0

where R is a function of the depolarizing factors L

j¼a;b;c

þð1  L

Þ"

The superscripts m and i refer to the host matrix phase and the inclusion phase. In

the self-consistent formula, the superscript

on R indicates that e

should be replaced

by "



in the expression for R. Depolarizing factors and the coefficient R for some

416 Electrical properties