Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

results – specifically V

¼ 0atV

¼ 1.06 km/s, which is slower than the V

for water.

Vernik et al. (2002) developed a nonlinear regression for brine-saturated sandstones

that honors the observed high-velocity limit for arenites (V

 5.48 km/s, V



3.53 km/s) and the velocity of a quartz–water suspension (V

 1.7 km/s at V

¼ 0)

at a critical porosity f  0.4:

¼1:267 þ 0:372V

þ 0:002 84 V



1=2

ðkm=sÞ

Their corresponding expression for shale is

¼0:79 þ 0:287V

þ 0:002 84V



1=2

ðkm=sÞ

Williams’s relation

Williams (1990) used empirical V

–V

relations from acoustic logs to differentiate

hydrocarbon-bearing sandstones from water-bearing sandstones and shales statistic-

ally. His least-squares regressions are:

¼ 1:182 þ 0:004 22 t

(water-bearing sands)

¼ 1:276 þ 0:003 74 t

(shales)

where Dt

is the shear-wave slowness in ms/ft. The effect of replacing water with

more compressible hydrocarbons is a large decrease in P-wave velocity with little

change (slight increase) in S-wave velocity. This causes a large reduction in the V

ratio in hydrocarbon sands compared with water-saturated sands having a similar Dt

A measured V

and Dt

is classified as either water-bearing or hydrocarbon-

bearing by comparing it with the regression and using a statistically determined

threshold to make the decision. Williams chose the threshold so that the probability

of correctly identifying a water-saturated sandstone is 95%. For this threshold a

measured V

is classified as water-bearing if

ðmeasuredÞmin½V

ðsandÞ; V

ðshaleÞ  0:09

and as potentially hydrocarbon-bearing otherwise. Williams found that when Dt

130 ms/ft (or Dt

< 75 ms/ft), the rock is too stiff to give any statistically significant

anomaly upon fluid substitution.

Xu and White’s relation

Xu and White (1995) developed a theoretical model for velocities in shaley sand-

stones. The formulation uses the Kuster–Tokso

z and differential effective-medium

theories to estimate the dry rock P- and S-velocities, and the low-frequency

377 7.9 V

–V

relations

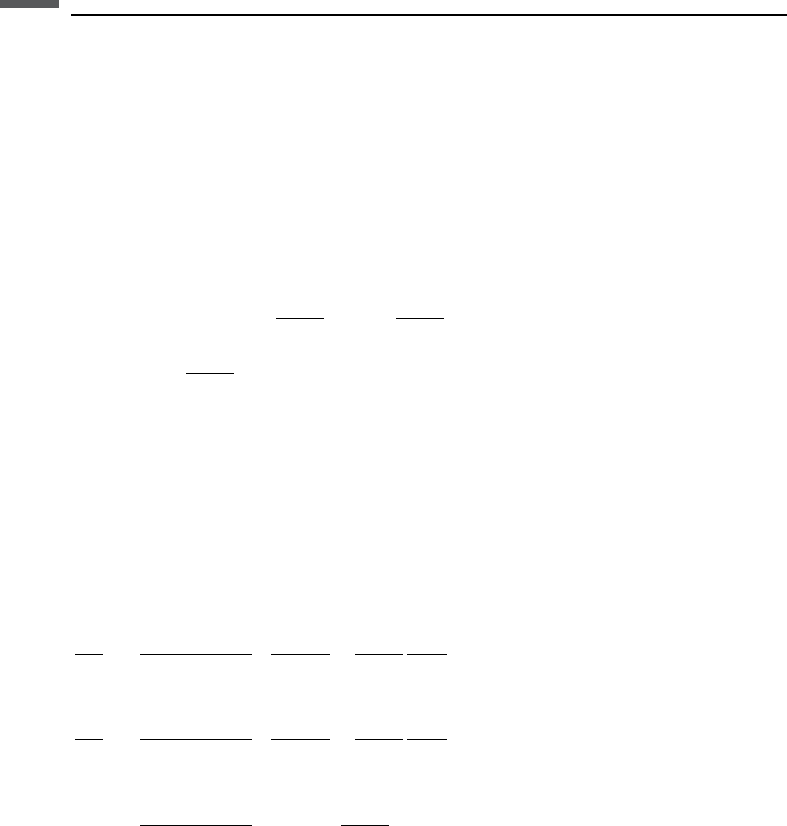
saturated velocities are obtained from Gassmann’s equation. The sand–clay

mixture is modeled with ellipsoidal inclusions of two different aspect ratios.

The sand fraction has stiffer pores w ith aspect ratio a  0.1–0.15, whereas the

clay-related pores are more compliant with a  0.02–0.05. The velocity model

simulates the “V”-shaped velocity–porosity relation of Marion et al. (1992)for

sand–clay mixtures. The total porosity f ¼ f

sand

þ f

clay,

where f

sand

and f

clay

are the porosities associated with the sand and clay fractions, respectively. These

are approximated by



sand

¼ð1    V

clay



1  

¼ V

sand



1  



clay

¼ V

clay



1  

where V

sand

and V

clay

denote the volumetric sand and clay content, respectively. The

shale volume from logs may be used as an estimate of V

clay

. Though the log-derived

shale volume includes silts and overestimates clay content, results obtained by Xu

and White justify its use. The properties of the solid mineral mixture are estimated by

a Wyllie time average of the quartz and clay mineral velocities and arithmetic

average of their densities by

1    V

clay

1  



Pquartz

clay

1  

clay

1    V

clay

1  



Squartz

clay

1  

clay



1    V

clay

1  





quartz

clay

1  



clay

where the subscript 0 denotes the mineral properties. These mineral properties are

then used in the Kuster–Tokso

z formulation along with the porosity and clay content

to calculate dry-rock moduli and velocities. The limitation of small-pore concen-

tration of the Kuster–Tokso

z model is handled by incrementally adding the pores in

small steps so that the noninteraction criterion is satisfied in each step. Gassmann’s

equations are used to obtain low-frequency saturated velocities. High-frequency

saturated velocities are calculated by using fluid-filled ellipsoidal inclusions in the

Kuster–Tokso

z model.

The model can be used to predict shear-wave velocities (Xu and White, 1994).

Estimates of V

may be obtained from known mineral matrix properties and measured

porosity and clay content or from measured V

and either porosity or clay content.

378 Empirical relations

Xu and White recommend using measurements of P-wave sonic log because it is

more reliable than estimates of shale volume and porosity.

Raymer-form V

prediction

Dvorkin (2007, personal c ommu nication) uses the Ra yme r–Hunt–Gardner func-

tional form V

¼ð1  Þ

þ V

,whereV

and V

denote the P-wave vel-

ocity in the solid and in the pore-fluid phases, respectively, and f is the total

porosity, to relate the S-wave velocity in dry rock to porosity and mineralogy as

Sdry

¼ð1  Þ

,whereV

is the S-wave velocity in the solid phase. Assum-

ing that the shear modulus of rock does not depend on the pore f luid, V

in wet

rock is V

Swet

¼ V

Sdry

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



bdry

=

bwet

,wherer

bdry

and r

bwet

denote the bulk density of

the dry and wet r ock, r espectively. This equation for V

prediction r eit erate s the

critical porosity concept of Nur et al. (1995): the V

ratioindryrockequals

that in the solid phase. However, the velocity–porosity trend that follows from this

equation differ s somewhat fr om the traditional critical porosity trend. This V

predictor exhibits a velocity–porosity trend essentially identical to that from the

stiff-sand (the modified lower Hashin–Shtrikman) model (Figure 7.9.13).

Uses

The relations discussed in this section can be used to relate P- and S-velocity and

porosity empirically for use in lithology detection and direct fluid identification.

Assumptions and limitations

Strictly speaking, the empirical relations discussed in this section apply only to the set

of rocks studied.

0 0.1 0.2 0.3 0.4

(km/s)

Porosity

Brine-saturated pure quartz rock

0 0.1 0.2 0.3 0.4

(km/s)

Porosity

Figure 7.9.13 The stiff-sand (slender curves), critical porosity (dashed curves labeled “CP”), and

RHG velocity predictions (heavy curves, labeled “R”) for P- (left) and S-wave (right) velocity in

pure-quartz, brine-saturated rock.

379 7.9 V

–V

relations

7.10 Velocity–density relations

Synopsis

Many seismic modeling and interpretation schemes require, as a minimum, P-wave

velocity V

, S-wave velocity, V

, and bulk density r

. Laboratory and log measure-

ments can often yield all three together. But there are many applications where only

is known, and density or V

must be estimated empirically from V

. Section 7.9

summarizes some V

–V

relations. Here we summarize some popular and useful V

–

density relations. Castagna et al. (1993) give a very good summary of the topic. See

also Section 7.8 on Brocher’s relations.

Density is a simple volumetric average of the rock constituent densities and is

closely related to porosity by



¼ð1  Þ

þ 

where r

is the density of mineral grains, r

is the density of pore fluids, and f is

porosity.

The problem is that velocity is often not very well related to porosity (and there-

fore to density). Cracks and crack-like flaws and grain boundaries can substan-

tially decrease V

and V

, even though the cracks may have near-zero porosity.

Table 7.10.1 Polynomial and power-law forms of the Gardner et al. (1974)

velocity–density relationships presented by Castagna et al. (1993). Units are km/s

and g/cm

for velocity and density, respectively.

Coefficients for the equation r

¼ aV

þ bV

þ c

Lithology abcV

range (km/s)

Shale –0.0261 0.373 1.458 1.5–5.0

Sandstone –0.0115 0.261 1.515 1.5–6.0

Limestone –0.0296 0.461 0.963 3.5–6.4

Dolomite –0.0235 0.390 1.242 4.5–7.1

Anhydrite –0.0203 0.321 1.732 4.6–7.4

Coefficients for the equation r

¼ dV

Lithology df V

range (km/s)

Shale 1.75 0.265 1.5–5.0

Sandstone 1.66 0.261 1.5–6.0

Limestone

1.36 0.386 3.5–6.4

Dolomite 1.74 0.252 4.5–7.1

Anhydrite 2.19 0.160 4.6–7.4

Note:

Coefficients for limestone have been revised here to better reflect observed trends.

380 Empirical relations

Velocity–porosity relations can be improved by fluid saturation and high effective

pressures, both of which minimize the effect of these cracks. Consequently, we also

expect velocity–density relations to be more reliable under high effective pressures

and fluid saturation.

Gardner et al. (1974) suggested a useful empirical relation between P-wave

velocity and density that represents an average over many rock types:



 1:741 V

0:25

where V

is in km/s and r

is in g/cm

,or



 0:23 V

0:25

where V

is in ft/s.

1.8 2 2.2 2.4 2.6 2.8

Shales

(km/s)

Density (

/cm

)

r = 1.75V

0.265

r = –0.0261V

+ 0.373V

+ 1.458

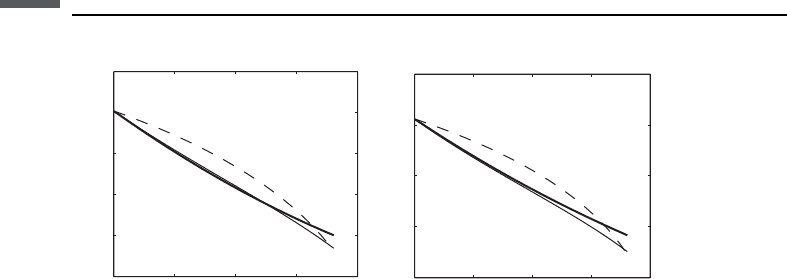
Figure 7.10.1 Both forms of Gardner’s relations applied to log and laboratory shale data, as

presented by Castagna et al. (1993).

1.8 2 2.2 2.4 2.6 2.8

Sandstones

(km/s)

Density (g/cm

)

r = 1.66V

0.261

r = −0.0115V

+ 0.261V

+ 1.515

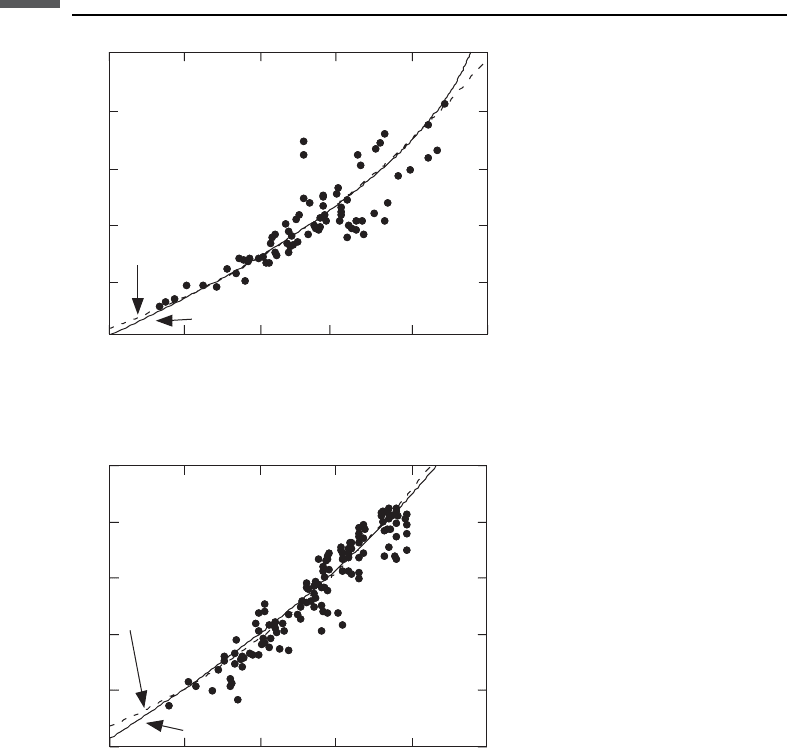
Figure 7.10.2 Both forms of Gardner’s relations applied to log and laboratory sandstone data,

as presented by Castagna et al. (1993).

381 7.10 Velocity–density relations

More useful predictions can be obtained by using the lithology-specific forms

given by Gardner et al. (1974). Castagna et al. (1993) suggested slight improvements

to Gardner’s relations and summarized these, as shown in Table 7.10.1, in both

polynomial and power-law form. Figures 7.10.1–7.10.4 show Gardner’s relations

applied to laboratory data.

Assumption and limitations

Gardner’s relations are empirical.

2 2.2 2.4 2.6 2.8 3

Dolomite

(km/s)

Density (g/cm

)

r = −0.0235V

+ 0.390V

+ 1.242

r = 1.74V

0.252

Figure 7.10.4 Both forms of Gardner’s relations applied to laboratory dolomite data.

1.8 2 2.2 2.4 2.6 2.8

Limestones

(km/s)

Density (g/cm

)

r = −0.0296V

+ 0.461V

+ 0.963

r = 1.5 V

0.225

r = 1.36 V

0.386

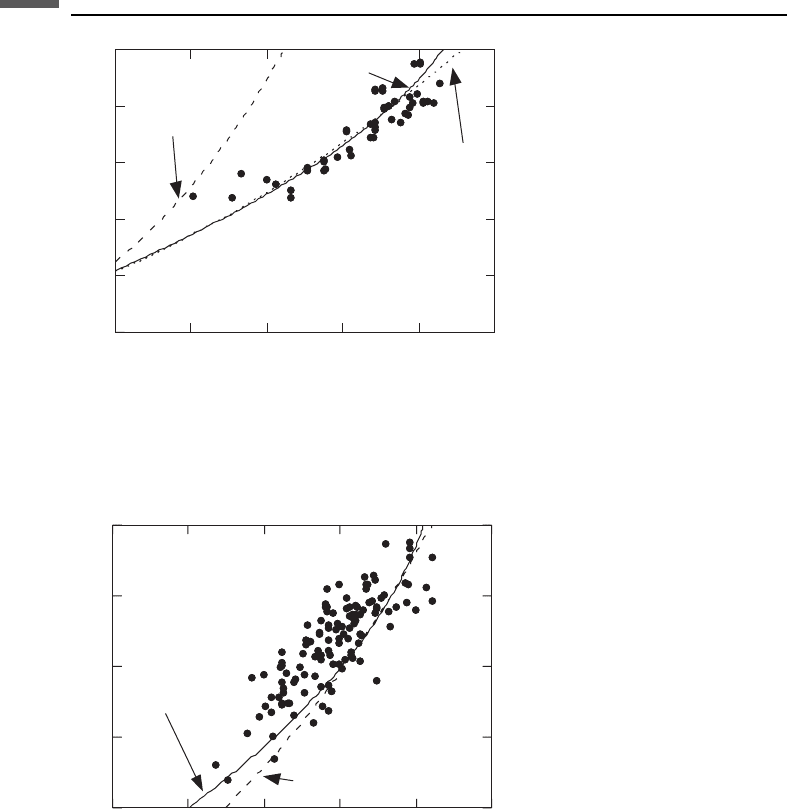
Figure 7.10.3 Both forms of Gardner’s relations applied to laboratory limestone data. Note that

the published power-law form does not fit as well as the polynomial. We also show a revised

power-law form fit to these data, which agrees very well with the polynomial.

382 Empirical relations

7.11 Eaton and Bowers pore-pressure relations

Synopsis

Following Eaton (1975), Gutierrez et al. (2006) present the following equation for

pore-pressure prediction from measured P-wave velocity:

over

 P

¼ðP

over

 P

hyd

ÞðV

where P

is the actual pore pressure, P

over

is the vertical overburden stress, P

hyd

is the

normal hydrostatic pressure, V

is the measured velocity, and V

is the normal-

compaction velocity. This equation implies that if V

¼ V

, i.e., the rock is normally

compacted, P

¼ P

hyd

. Conversely, if V

< V

, i.e., the measured velocity is smaller

than the normal velocity, P

> P

hyd

, which means that the rock is overpressured. The

Eaton equation is applicable to overpressure due to undercompaction of shale which

occurs during monotonic overburden stress increase due to burial.

Bowers (1995) considers overpressure generation not only due to undercompaction

but also due to tectonic unloading, such as occurs during uplift of rock. Gutierrez

et al. (2006) present Bowers’s equation as

over

 P

¼½ðV

 5000Þ=a

1=b

where pressure is in psi and velocity is in ft/s. The coefficients calibrated to the monotonic-

compa ction data from the Gulf of Mexico are a ¼ 9.18448 and b ¼ 0.764984. These

coefficients may be different in environments whe re abnormal pore pressure is

generated by unloading, kerogen maturation, or clay mineral transformations.

Assumption and limitations

The constants and trends used in these equations are highly site-specific and require

thorough calibration using real pore-pressure measurements. As a result, we caution

against using the constants appropiate for one basin at another location. Moreover, these

constants may vary even within the same basin between different fault blocks. The

normal compaction trends for the P-wave velocity are sometimes simply not present in

basins where all drilled wells encounter overpressure, i.e., the measured velocity is

always abnormally slow. In this case, an assumed normal velocity trend has to be adopted.

7.12 Kan and Swan pore-pressure relations

Synopsis

Hottman and Johnson (1965) established an empirical relation between the pore-

pressure gradient, P(z)/z, and Dt, the departure of sonic interval transit time from a

383 7.12 Kan and Swan pore-pressure relations

background trend of transit time with depth. The background trend is for normally

pressured shale undergoing normal compaction. The relation is given by

PðzÞ=z ¼ R

þ c

t þ c

tðÞ

where R

is the hydrostatic pore-pressure gradient (in Pa/m), z is the depth in meters,

and t ¼ tðzÞt

expðz=kÞ is the interval transit time departure in ms/m.

The normal compaction shale trend is given by t

exp(z/k), where t

is the transit

time of the shale at z ¼ 0 and k is determined from log data in normally pressured

shale. Kan and Swan (2001) give a compilation of coefficients c

and c

for specific

basins and ages, determined by empirical regression (Table 7.12.1). With the appro-

priate coefficients, Kan and Swan expect the empirical equation to be reasonably

accurate for pressure gradients up to 20 kPa/m as long as the overpressure is caused

only by undercompaction.

Assumption and limitations



The relation is empirical.



The relation applies strictly only to overpressure caused by undercompaction and

not to other mechanisms such as aquathermal pressure, kerogen maturation, and

other late-stage mechanisms.

7.13 Attenuation and quality factor relations

Klimentos and McCann (1990) present a statistical relation between the compres-

sional-wave attenuation coefficient a (measured in dB/cm), porosity f, and clay

content C (both measured in volume fraction) obtained in water-saturated sandstone

samples. The porosity of the samples ranges from 0.05 to 0.30, and the clay content

ranges from zero to 0.25. The differential pressure is 40 MPa and the frequency is

1 MHz. The relation is

Table 7.12.1 Kan and Swan’s (2001) empirical coefficients.

Basin and age c

(Pa/ms) c

(Pa · m/ms

)

Gulf of Mexico Miocene 143 –0.42

Gulf of Mexico Pliocene 67.6 –0.10

Gulf of Mexico Pleistocene 42.7 –0.028

North Sea 13.1 0.168

Alaska 36.5 0.48

Northwest Australia 42.4 0.22

South China Sea 32.8 1.54

384 Empirical relations

 ¼ 3:15 þ 24:1C  0:132

with a correlation coefficient of 0.88.

Koesoemadinata and McMechan (2001) use a large number of experimental results

in sandstones to obtain statistical relations between the P- and S-wave inverse quality

factors and the effective pressure, porosity, clay content, water saturation, permeabil-

ity, and frequency. Figures 7.13.1 and 7.13.2 display selected results from these

relations.

Uses

These relations can be used to estimate attenuation versus porosity, clay content,

saturation, frequency, pressure, and permeability.

0.1 0.2 0.3 0.4

0.1

0.2

= 0.5

Porosity

1/Q

0.1 0.2 0.3 0.4

0.1

0.2

= 0.5

Porosity

1/Q

Clay

fraction

0.50

0.25

0.0

Clay

fraction

0.50

0.25

0.0

Figure 7.13.2 Same as Figure 7.13.1 but with a water saturation of 0.5. Again, the clay content is

zero, 0.25, and 0.5 (from bottom to top). The effective pressure is 30 MPa, frequency is 1 MHz, and

permeability is 100 mD. The inverse quality factors increase with increasing clay content.

0.1 0.2 0.3 0.4

0.1

0.05

= 1.0

Porosity

1/Q

0.1 0.2 0.3 0.4

0.1

0.05

= 1.0

Porosity

1/Q

Clay

fraction

0.50

0.25

0.0

Clay

fraction

0.50

0.25

0.0

Figure 7.13.1 The P- and S-wave inverse quality factors in fully water-saturated sandstone

versus porosity for a clay content of zero, 0.25, and 0.5 (from bottom to top). The effective pressure

is 30 MPa, the frequency is 1 MHz, and the permeability is 100 mD. The inverse quality factors

increase with increasing clay content.

385 7.13 Attenuation and quality factor relations

Assumptions and limitations

These relations are strictly empirical and mostly valid at laboratory ultrasonic

frequencies. They may not be applicable in the well-log, VSP, and/or seismic

frequency ranges.

7.14 Velocity–porosity–strength relations

Synopsis

Chang et al. (2004) and Zoback (2007), summarize 30 empirical equations relating

physical properties (such as velocity, Young’s modulus, and porosity) to unconfined

compressive strength (UCS) in sandstone, shale, and limestone and dolomite; see

Tables 7.14.1–7.14.3. While some equations work reasonably well (for example, some

strength–porosity relationships for sandstone and shale), data on rock strength show

considerable scatter around the empirical regressions, emphasizing the importance of

local calibration before utilizing any of the relationships presented. Nonetheless, some

reasonable correlations can be found between velocity, porosity, and rock strength that

can be used for applications related to well-bore stability, where having a lower-bound

estimate of rock strength is especially useful.

Table 7.14.1 Empirical relations for sandstones (Chang et al., 2004; Zoback, 2007).

UCS ¼

Equation

number

0.035 V

– 31.5 Thuringia, Germany; Freyburg (1972) (1)

1200 exp(0.036Dt) Bowen Basin, Australia. Fine-grained consolidated

and unconsolidated sandstone; McNally (1987)

(2)

1.4138 10

–3

Gulf Coast, weak unconsolidated sandstone (3)

3.3 10

–20

 Gulf Coast sandstones with UCS > 30 MPa;

Fjaer et al. (2008)

(4)

[(1þn)/(1n)]



(1–2n)[1þ0.78V

clay

]

1.745 10

–9

– 21 Cook Inlet, Alaska; coarse-grained sandstone and

conglomerates; Moos et al. (1999)

(5)

42.1 exp(1.9 10

–11

) Australia; consolidated sandstones with UCS

>80 MPa, porosity between 0.05 and 0.12;

Chang et al. (2004)

(6)

3.87 exp(1.14 10

–10

) Gulf of Mexico; Chang et al. (2004) (7)

46.2 exp(0.027E) Chang et al. (2004) (8)

2.28 þ4.1089E Worldwide; Bradford et al. (1998) (9)

254(1 – 2.7f)

Worldwide; very clean, well-consolidated

sandstones with porosity < 0.3;

Vernik et al. (1993)

(10)

277 exp(–10f) Sandstones with 2 < UCS < 360 MPa, and

0.002 < f < 0.3; Chang et al. (2004)

(11)

386 Empirical relations