Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

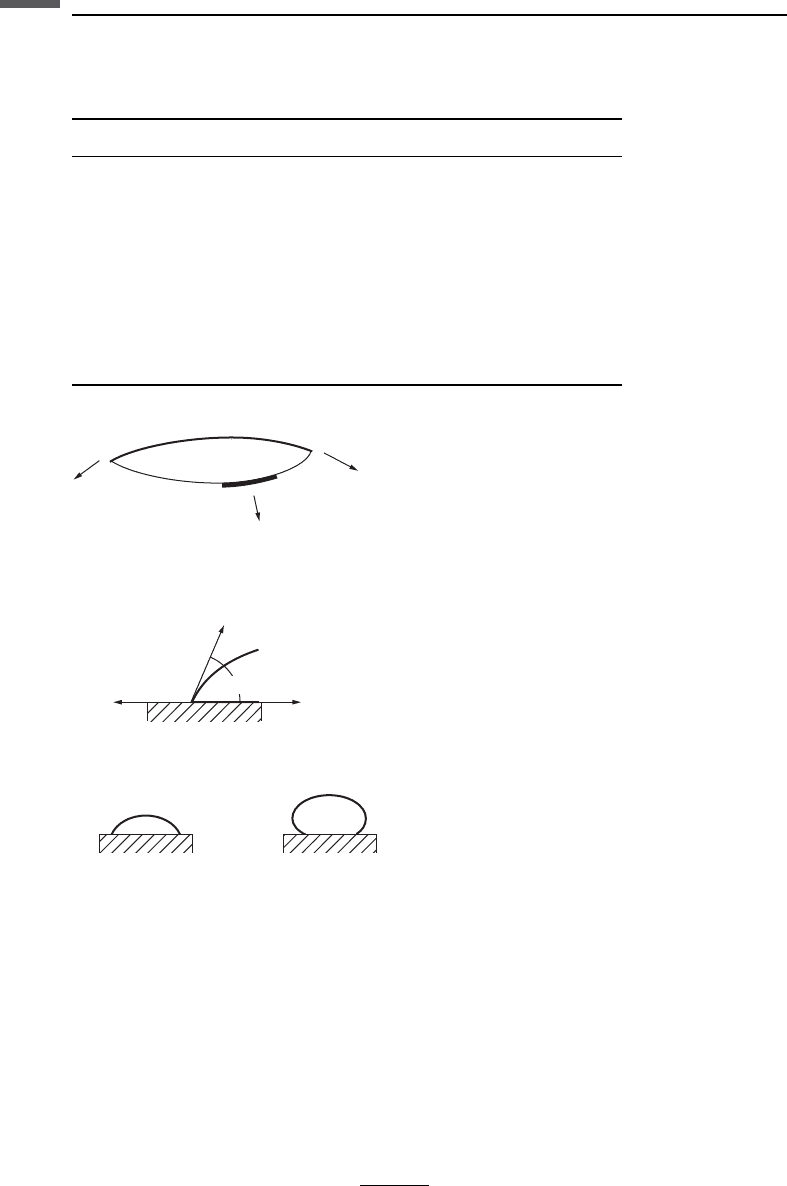
the interface surface. If t is a force acting on length l of the surface, then the surface

tension is defined as g ¼ t=l; hence, the unit of surface tension is force per unit length

(N/m). A surface tension may be different at interfaces between different materials.

For example, g

(oil–water) differs from g

(oil–gas) and from g

(water–gas).

Some typical values of fluid–fluid surface tensions are shown in Table 8.3.1.

The force equilibrium condition at a triple point of contact between a solid, a

liquid, and a gas is given by (Figure 8.3.2) Young’s relation:

cosðyÞþg

¼ g

; cosðyÞ¼

 g

Figure 8.3.1 Surface tensional forces at a liquid–solid or liquid–liquid interface.

Table 8.3.1 Typical values for surface tension (at 20



C, unless

otherwise noted).

Interface g in mN/m

Water–air 72.80

Octane–air 21.62

Heptane–air 20.14

Mercury–air 486.5

Water–mercury 415

Ethylene glycol–air (25



C) 47.3

Benzene–air 28.88

Toluene–air 28.52

Ethanol–air 22.39

Triple junction:

gas–liquid–solid

Gas

Liquid

Solid

Wetting fluid Non–wetting fluid

Figure 8.3.2 Triple junction at the interface between a solid, a liquid, and a gas.

Top: the contact angle at the triple junction. Bottom: schematic of wetting and nonwetting fluids.

397 8.3 Capillary forces

where g

, g

, and g

are the liquid–gas, liquid–solid, and gas–solid interfacial

tensions, respectively. The angle y is the contact angle. The liquid within the droplet

is wetting if y < 90



and nonwetting if y > 90



. The equilibrium will not exist if

jðg

 g

Þ=g

j > 1

A similar situation can occur at the triple interface of a solid and two immiscible liquids.

The surface tension between a solid and liquid is difficult to measure. Some techniques

are based on directly measuring the contact angle of a drop (goniometry), while others are

based on measurements of the force of interaction between the solid and a test liquid

(tensiometry). The observed contact angle can be affected by the liquid and solid

compositions, the surface roughness, temperature, pressure, heterogeneity along the

surface, and the amount of time elapsed since the liquid and solid came into contact.

The contact angle for a fluid contact advancing (or recently advanced) along the solid

surface is usually larger than the contact angle on a receding (or recently receded) contact.

Ifasphereofoil(radiusR) is floating inside water, the oil–water surface tension, g,has

the effect of contracting the sphere, causing the pressure inside the sphere, P

,tobegreater

than pressure in the surrounding water P

. The difference between these two pressures

is called capillary pressure: P

¼ P

 P

and is given by the Laplace equation:

¼ 2g=R

In general, capillary pressure inside a surface of two principal radii of curvature

and R

¼ g





where the plus sign corresponds to the case in which the centers of curvature are

located on the same side of the interface (e.g., a sphere), and the minus sign

corresponds to the case in which the centers of the curvature are located on opposite

sides (e.g., a torus).

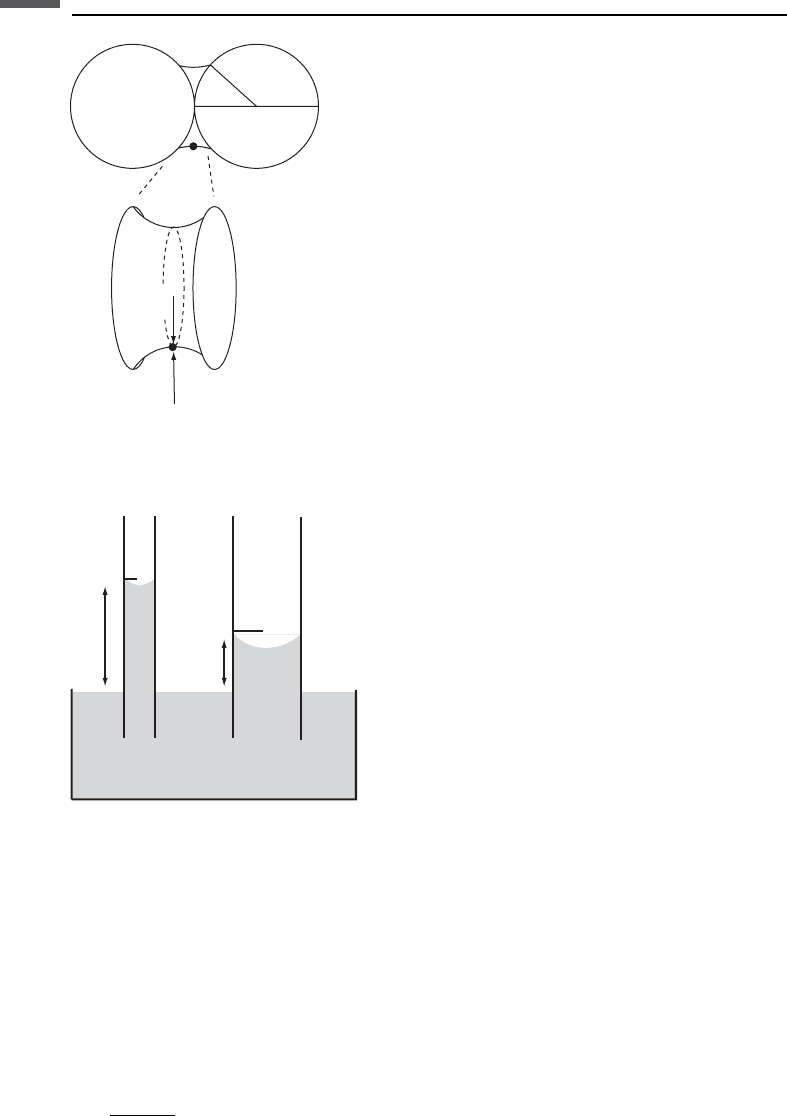
If the pore fluid is wetting, a pendular ring may exist at the point of contact of two

grains (see Figure 8.3.3). The capillary pressure at any point P on the surface of the

ring depends on the contact angle y of the liquid with the grains and on the radii of

curvature, R

and R

, at that point, as follows:

¼ g





cosðyÞ

If y ¼0, we have the following expression at the contact point of two identical

spherical grains of radius R (Gvirtzman and Roberts, 1991):

¼ R

sinðÞþcosðÞ1

cosðÞ

; R

¼ R

1  cosðÞ

cosðÞ

where f is the angle between the line connecting the centers of the spheres and the line

from the center of the sphere to the edge of the pendular ring. The ring will exist as long

398 Flow and diffusion

as its capillary pressure is smaller than the external pressure. The preceding formulas

show that this condition is valid for f < 53



. The maximum volume of this ring is about

0.09 times the volume of an individual grain. This maximum volume tends to decrease

with increasing angle y (e.g., it is 0.04 times the grain volume for y ¼32



When a narrow tube is brought into contact with a wetting liquid, the liquid rises

inside the tube (see Figure 8.3.4). The weight of the fluid column is supported by the

capillary forces. The height of this rise (h)is

h ¼

2g cos y

gr

where g is the surface tension between the two fluids in the tube; y is the contact angle

of the wetting liquid on the tube surface; Dr is the density contrast of the fluids

Figure 8.3.3 A pendular ring of fluid between two grains, showing the two radii

of curvature at point P.

Figure 8.3.4 Capillary rise of a wetting fluid inside tubes of different radii.

399 8.3 Capillary forces

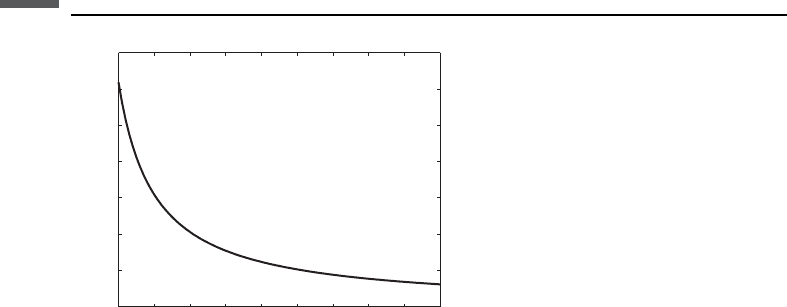
(approximately 1000 kg/m

for a water–air system); g is the acceleration due to

gravity (9.8 m/s

); and r is the radius of the tube. For a tube containing water and

air with surface tension at room conditions of about 0.07 N/m, and assuming a contact

angle of 30



, we plot the capillary equilibrium height versus the tube radius in

Figure 8.3.5.

Imbibition refers to the increase of the wetting-fluid saturation in a rock, while

drainage refers to the decrease of the wetting-fluid saturation. Imagine a rock fully

saturated with water, the wetting phase. If the rock is put in contact with oil (the

nonwetting phase), the oil will not enter the pore space because of the capillary forces

holding the water in place. If the oil is pressurized to the capillary pressure of the

largest pore throats, oil will begin to enter (drainage). Further increases in oil pressure

will allow the oil to be forced into successively smaller and smaller throats, until

eventually a limit is reached, corresponding to the irreducible water saturation

(see Figure 8.3.6). Dropping the oil pressure causes the water to re-enter the rock,

displacing oil. The saturation–pressure curve for imbibition will generally be different

than the curve for drainage (see Figure 8.3.6). At zero oil pressure, some residual oil

will remain in the rock, trapped in bypassed pores.

Uses

The formulas presented in this section can be used to calculate wetting pore-fluid

geometry in granular rocks.

Assumptions and limitations

Some of the formulas in this section are based on idealized geometries. For example,

the description of pendular rings is for spherical grains. The equation for capillary rise

is for tubes of circular cross-section.

2345678910

Capillary radius (mm)

Capillary height (mm)

Figure 8.3.5 Capillary rise of a wetting fluid as a function of tube radius, for an air–water

system with a contact angle of 30



400 Flow and diffusion

8.4 Kozeny–Carman relation for flow

Synopsis

The Kozeny–Carman (Carman, 1961) relation provides a way to estimate the per-

meability of a porous medium in terms of generalized parameters such as porosity,

surface area, and particle size. The derivation is based on flow through a pipe having

a circular cross-section with radius R. The flux in the pipe of length l can be written as

Q ¼

8

P

where P is the pressure and  is the dynamic viscosity. Assume that the direction of this

pipe is at an angle to the pressure gradient, which is applied to a permeable block of

length L (L l) and cross-sectional area A (Figure 8.4.1). Comparison with Darcy’s law,

Q ¼k



P

where k is the permeability, gives an effective permeability for the block expressed as

k ¼

8At

20 30 40 50 60 70 80 90 100

Water saturation (%)

Capillary pressure (Hg cm)

Imbibition

Drainage

Irreducible

water

Residual

oil

Figure 8.3.6 Typical imbibition–drainage curves for a water-wet rock.

401 8.4 Kozeny–Carman relation for flow

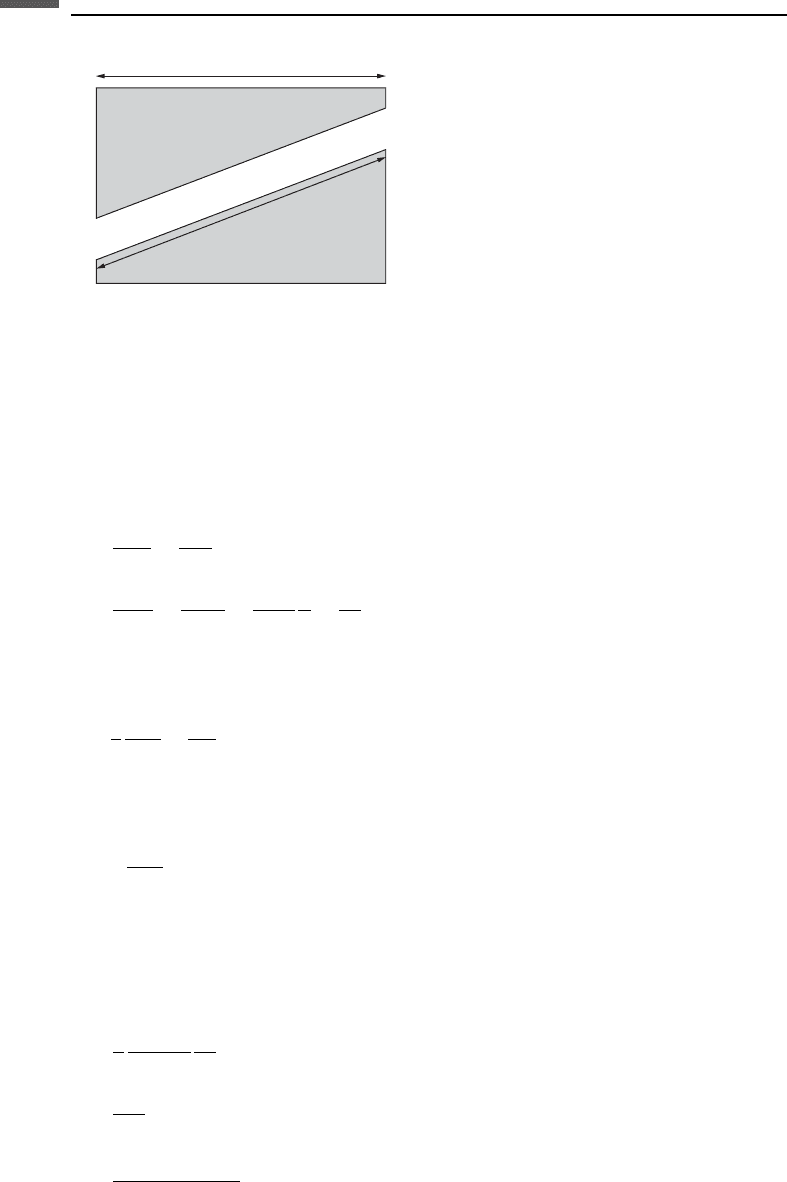
where t is the tortuosity (defined as the ratio of total flow-path length to length of the

sample).

The porosity, f, and the specific surface area, S (defined as the pore surface area

divided by the sample volume), can be expressed in terms of the properties of the pipe

by the following relations:

 ¼

S ¼

2pRl

2pRt

2

Finally, we can express the permeability of the block with the pipe in terms of the

more general properties, f and S, to obtain the Kozeny–Carman relation:

k ¼



This relation, which is exact for an ideal circular pipe geometry, is often presented in

general terms as

k ¼ B



where B is a geometric factor that accounts for the irregularities of pore shapes.

The exact expressions for viscous flow through pipes of elliptical, square, and

triangular cross-sections allows us to derive the Kozeny–Carman relations for these

shapes. Specifically, for the elliptical cross-section with semiaxes a and b,

k ¼

þ b

 ¼

pab

S ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2ða

þ b

Figure 8.4.1 Solid block with a pipe used for Kozeny–Carman derivations. The notation

is explained in the text.

402 Flow and diffusion

Then,

k ¼

1 þðb=aÞ



which implies the universality of the latter expression for pores of elliptical cross-

section.

Similarly, for a square pipe whose side is a,

k ¼ 0:035144 a



¼ 0:562



and for a pipe of equilateral triangular cross-section,

k ¼

a

80t

¼ 0:6



Notice that the factors of similar magnitude (0.5, 0.562, and 0.6) relate permeability

to 

in these three pipe geometries.

A common extension of the Kozeny–Carman relation for a circular pipe is to

consider a packing of identical spheres of diameter d. Although this granular pore-

space geometry is not consistent with the pipe-like geometry, it is common to use the

original Kozeny–Carman functional form. This allows a direct estimate of the

specific surface area in terms of the porosity, S ¼6(1–f)/d, which leads to the

permeability expression

k ¼



ð1  Þ

k ¼ B



ð1  Þ

where the factor of 1/72 and the tortuosity have been absorbed into the constant B.

Bourbie

et al. (1987) discuss a more general form,

/ 

in which n has been observed experimentally to vary with porosity from n  7

(f < 5%) to n  2(f > 30%). The Kozeny–Carman value of n ¼3 appears to be

appropriate for very clean materials such as Fontainebleau sandstone and sintered

glass, whereas n ¼4 or 5 is probably more appropriate for more general natural

materials (Bourbie

et al., 1987).

Mavko and Nur (1997) suggest that one explanation for the apparent dependence of

the coefficient, n, on porosity is the existence of a percolation porosity, 

, below

which the remaining porosity is disconnected and does not contribute to flow.

403 8.4 Kozeny–Carman relation for flow

Experiments suggest that this percolation porosity is of the order of 1–3%, although it

depends on the mechanism of porosity reduction. The percolation effect can be

incorporated into the Kozeny–Carman relations simply by replacing f by ð  

Þ.

The idea is that it is only the porosity in excess of the threshold porosity that

determines the permeability. Substituting this into the Kozeny–Carman equation

gives

ð  

½1 ð  

Þ

k ¼B

ð  

ð1 þ 

 Þ

Bð  

The result is that the derived n ¼3 behavior can be retained while fitting the

permeability behavior over a large range in porosity.

Remember that in all of the above formulations of the Kozeny–Carman relation,

the unit of permeability is length squared (e.g., m

), where the length unit is that used

for the pipe radius or particle size (e.g., m). The porosity is expressed as a unitless volume

fraction, and the unit of the specific surface area is the inverse length (e.g., m

–1

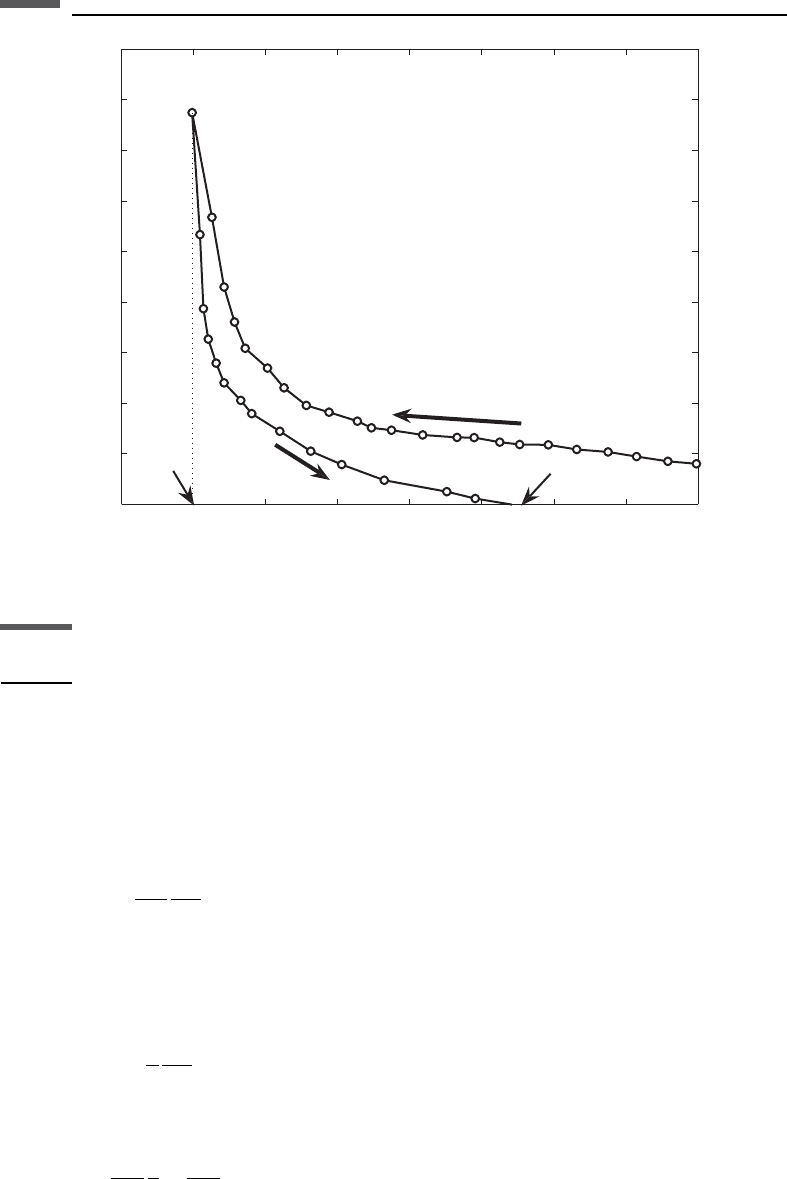
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

−2

Permeability (mD)

Porosity

Fontainebleau sandstone

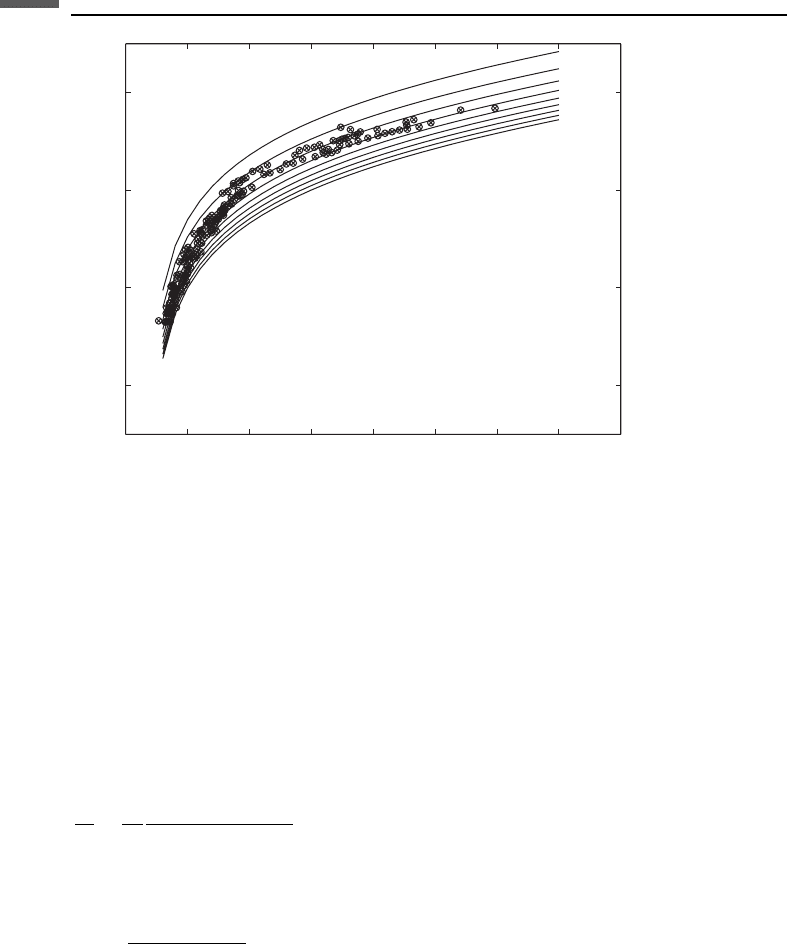
Figure 8.4.2 Permeability versus porosity for the Fontainebleau dataset with theoretical curves

superimposed according to the Kozeny–Carman equation. The threshold porosity is 0.02,

and the tortuosity varies from 1 (upper curve) to 5 (lower curve) with a constant increment of 0.5.

404 Flow and diffusion

The same equation for permeability in milliDarcy, particle size in mm, and

porosity in fraction of unity reads as

ð  

½1 ð  

Þ

Figure 8.4.2 compares laboratory permeability data of Fontainebleau sandstone

with permeability calculations according to the above Kozeny–Carman equation. The

threshold porosity is 0.02, and tortuosity varies from 1 (upper curve) to 5 (lower

curve) with constant increment 0.5. The grain size is 0.25 mm. The apparent tortuosity

values appropriate for this dataset are between 1.5 and 3.

Calculate the permeability of a sandstone sample which has porosity 0.32 and an

average grain size of 100 mm. Use the Kozeny–Carman relation modified for a

percolation porosity:

k ¼ B

ð  

ð1 þ 

 Þ

Assume that B ¼15 and f

¼0.035. The units of B in this equation are such that

expressing d in microns gives permeability in milliDarcy. Then

k ¼B

ð  

ð1 þ 

 Þ

¼ 15

ð0:32 0:035Þ

ð1 þ 0:035  0:32Þ

100

¼6792:3 milliDarcy ¼ 6:79 Darcy

Compare the permeabilities k

and k

of two sandstones that have the same

porosity and pore microstructure, but different average grain sizes, d

¼80 m m

and d

¼240 mm.

Assuming that B and f

are the same for both sandstones since they have the same

pore microstructure, we can express the ratio of their permeabilities as

240

The sandstone with larger average grain size has a higher permeability (by a factor

of 9), even though both have the same total porosity.

Mixed particle sizes

Extensive tests (Rumpf and Gupte, 1971; Dullien, 1991) on laboratory data for

granular media with mixed particle sizes (poor sorting) suggest that the Kozeny–Carman

relation can still be applied using an effective or average particle size



D, defined by

405 8.4 Kozeny–Carman relation for flow



nðDÞdD

where n(D) is the number distribution of each size particle. This can be written in

terms of a discrete size distribution as follows:



This can be converted to a mass distribution by noting that

¼ n



¼ n

p



where m

, and r

are the mass, radius, and density of the ith particle size. Then, one

can write



ðm

=

ðm

=

If the densities of all particles are the same, then



ðm

where f

is either the mass fraction or the volume fraction of each particle size.

An equivalent description of the particle mixture is in terms of specific surface

areas. The specific surface area (pore surface area divided by bulk sample volume)

for a mixture of spherical particles is



S ¼ 3ð1  Þ

Uses

The Kozeny–Carman relation can be used to estimate the permeability from geomet-

ric properties of a rock.

Assumptions and limitations

The following assumptions and limitations apply to the Kozeny–Carman relation:



the derivation is heuristic. Strictly speaking, it should hold only for rocks with

porosity in the form of circular pipes. Nevertheless, in practice it often gives

reasonable results. When possible it should be tested and calibrated for the rocks

of interest;



the rock is isotropic; and



fluid-bearing rock is completely saturated.

406 Flow and diffusion