Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.

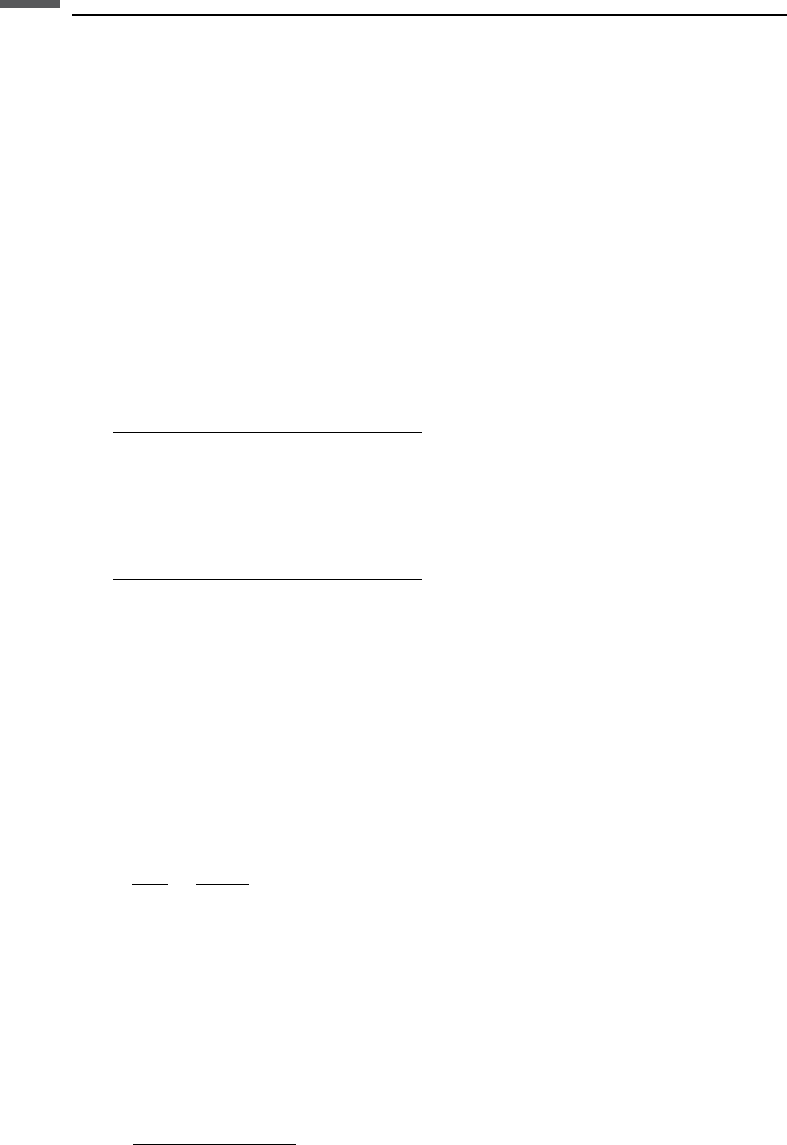
Note that here and in the following we use shaley sand equations F ¼ af
–m
and not
s
w
/s. The cation exchange capacity is a measure of the excess charges and Q
v
is the
charge per unit pore volume. Clays often have an excess negative electrical charge
within the sheet-like particles. This is compensated by positive counterions clinging
to the outside surface of the dry clay sheets. The resulting positive surface charge is a
property of the dry clay mineral and is called the cation exchange capacity (Clavier
et al., 1984). In the presence of an electrolytic solution such as brine, the electrical
forces holding the positive counterions at the clay surface are reduced. The counter-
ions can move along the surface contributing to the electrical conductivity. The
average mobility of the ions is described by B. The parameter B is a source of
uncertainty, and several expressions for it have been developed since the original
paper. Juha
´
sz (1981) gives the following expressions for B:
B ¼
5:41 þ 0:133T 1:253 10
4
T
2
1 þ R
1:23
w
ð0:025T 1:07Þ
where T is the temperature in degrees Fahrenheit or
B ¼
1:28 þ 0:225T 4:059 10
4
T
2
1 þ R
1:23
w
ð0:045T 0:27Þ
for temperature in degrees Celsius. Application of the Waxman–Smits equation
requires calibration with core CEC measurements, which are not always available.
The normalized Waxman–Smits or Waxman–Smits–Juha
´
sz model (Juha
´
sz, 1981)
does not require CEC data because it uses V
sh
derived from logs to estimate Q
v
by
normalizing it to the shale response. In this model
BQ
v
¼ Q
vn
ð
wsh
w
Þ
Q
vn
¼
Q
v
Q
vsh
¼
V
sh
sh
where f is the total porosity (density porosity), f
sh
is the total shale porosity, and
s
wsh
is the shale water conductivity obtained from s
wsh
¼ Fs
sh
, where s
sh
is the
conductivity of 100% brine-saturated shale. The normalized Q
v
ranges from 0 in
clean sands to 1 in shales. Brine saturation S
w
can be obtained from these models by
solving (Bilodeaux, 1997)
S
w
¼
FR
w
R
t
1 þ R
w
BQ
v
=S
w
ðÞ
1=n
427 9.4 Electrical conductivity in porous rocks

For n ¼ 2 the explicit solution (ignoring the negative root) is
S
w
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
FR
w
R
t
þ
BQ
v
R
w
2
2
s
BQ
v
R
w
2
The dual-water model divides the total water content into the bound clay water, for
which the conductivity depends only on the clay counterions, and the far water, away
from the clay, for which the conductivity corresponds to the ions in the bulk forma-
tion water (Clavier et al., 1984). The bound water reduces the water conductivity s
w
by a factor of (1 – av
Q
Q
v
). The dual-water model formula is (Clavier et al., 1984;
Sen and Goode, 1988)
¼
m
½
w
ð1 v
Q
Q
v
ÞþQ
v
where v
Q
is the amount of clay water associated with 1 milliequivalent of clay
counterions, b is the counterion mobility in the clay double layer, and a is the ratio
of the diffuse double-layer thickness to the bound water layer thickness. At high
salinities (salt concentration exceeding 0.35 mol/ml) a ¼ 1. At low salinities it is a
function of s
w
, and is given by
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1
n
1
hi
n
hi
s
where n
hi
is the salt concentration in bulk water at 25
C in mol/ml, g is the NaCl
activity coefficient at that concentration, n
1
hi
¼ 0:35 mol/ml, and g
1
= 0.71, i.e., the
corresponding NaCl activity coefficient.
Although v
Q
and b have a temperature and salinity dependence, Clavier et al.
(1984) recommend the following values for v
Q
and b:
v
Q
¼ 0:28 ml=meq
¼ 2:05 ðS=mÞ=ðmeq=cm
3
Þ
These values are based on analysis of CEC data for clays and conductivity data on
core samples. At low salinities, v
Q
varies with
ffiffiffi
T
p
and increases by about 26% from
25 to 200
C.
Generalizing from theoretical solutions for electrolytic conduction past charged
spheres in the presence of double layers, Sen and Goode (1988) proposed the
following shaley-sand equation:
¼
1
F
w
þ
AQ
v
1 þ CQ
v
=
w
þ EQ
v
428 Electrical properties

The constants A and C depend on pore geometry and ion mobility, and the term
EQ
v
accounts for conductivity by surface counterions even when water conductivity
is zero. Sen and Goode were able to express the relation in terms of Archie’s
exponent m by fitting to core data (about 140 cores)
¼
m
w
þ
m1:93Q
v
1 þ 0:7=
w
þ 1:3
m
Q
v
where conductivities are in mho/m and Q
v
is in meq/ml.
In the limit of no clay (Q
v
¼ 0) or no counterion mobility (A ¼ C ¼ 0) the
expression reduces to Archie’s equation. In the limits of high and low brine conduct-
ivity, with nonzero Q
v
, the expression becomes
¼
1
F
ð
w
þ AQ
v
ÞþEQ
v
; high-
w
limit
¼
1
F
1 þ
A
C
w
þ EQ
v
; low-
w
limit
At low s
w
the s versus s
w
curve has a higher slope than at the high-s
w
limit. At
high s
w
the electric current is more concentrated in the pore-space bulk fluid than in
the clay double layer, whereas for low s
w
the currents are mostly concentrated within
the double layer. This gives rise to the curvature in the s versus s
w
behavior.
Uses
The equations presented in this section can be used to interpret resistivity logs.
Assumptions and limitations
Models for log interpretation involve much empiricism, and empirical relations
should be calibrated to specific locations and formations.
9.5 Cross-property bounds and relations between elastic
and electrical parameters
Faust (1953) presents an empirical relation between the measured resistivity R
0
of a
water-saturated formation and V
P
:
V
P
¼ 2:2888 Z
R
0
R
w
1=6
where R
w
is the resistivity of formation water, Z is depth in km, and V
P
is in km/s.
429 9.5 Cross-property bounds and relations

Faust’s original form of the empirical relation is
Vðft=sÞ¼ Z½R
t
ðÞ
1=6
¼ 1948
where depth is in feet and ½R
t
is a dimensionless ratio of the average formation
resistivity to the average formation water resistivity.
Hacikoylu et al. (2006) show that this equation is only applicable for consolidated
sandstone with small clay content. Hacikoylu et al. (2006) use theoretical velocity–
porosity relations for soft sediment in combination with equations for the formation
factor to obtain a velocity–resistivity relation appropriate for soft sediment. They
show that this theoretical dependence can be approximated by the following equation:
V
P
¼
R
0
=R
w
0:9 þ cðR
0
=R
w
Þ
where V
P
is in km/s and the coefficient c varies between 0.27 and 0.32 for Gulf of
Mexico shale data.
Figure 9.5.1 displays V
P
versus the formation factor F ¼ R
0
=R
w
for both equations,
using Z ¼ 2 km and c ¼ 0.3.
Koesoemadinata and McMechan (2003) have given empirical relations between
the ultrasonic P-wave velocity (V
P
), dielectric constant (k), porosity (f), density (r),
and permeability (k). The regressions are based on data from about 30 samples of
Ferron sandstone, a fine- to medium-grained sandstone with porosity ranging from
1 10
100
2
3
4
5
Formation factor
V
P
(km/s)
Faust (1953)
Hacikoylu et al. (2006)
Figure 9.5.1 P-wave velocity versus formation factor according to the Faust (1953) and
Hacikoylu et al. (2006) equations.
430 Electrical properties

10% to 24% and clay content ranging from 10% to 22%. The V
P
and k data were
measured on dry (< 1% water saturation by volume) samples at 125 kHz and 50 MHz,
respectively.
¼ 0:001 19 V
P
þ 1:413 83
¼ 0:000 58 V
P
0:162 94 ln k þ 3:3758
¼ 0:000 72 V
P
0:068 51 þ 3:8133
¼ 0:000 72 V
P
þ 2:3032 2:4137
V
P
¼ 479:6734 þ 380:980
V
P
¼ 229:350 33 104:8169 ln k þ 1756:658
R
2
¼ 0:55
R
2
¼ 0:64
R
2
¼ 0:65
R
2
¼ 0:68
R
2
¼ 0:55
R
2
¼ 0:64
In the above empirical regressions V
P
is in m/s, permeability is in mD, density is in
g/cm
3
, porosity is given as a percentage, and k is dimensionless. R
2
is the coefficient
of determination for the regression.
Carcione et al. (2007) have compiled and derived cross-property relations and
bounds relating electrical conductivity to elastic moduli and velocities of rocks. The
cross-property relations are based on existing empirical and theoretical relations
between electrical conductivity and porosity and between elastic moduli and porosity.
The basic approach is as follows. If the relation between porosity, , and conductiv-
ity, , is described by ¼ f ðÞ, while the relation between elastic velocity v and
porosity is given by v ¼ gðÞ, then the cross-property relation can be obtained by
eliminating to give ¼ f ðg
1
ðvÞÞ.
Dry rocks
For a dry rock with randomly oriented penny-shaped cracks of zero conductivity in an
isotropic elastic medium, Bristow (1960) gave the following relations between dry-
rock elastic moduli and electrical conductivity:
Bristow
K
s
K
m
K
m
¼
21
2
s
1 2
s
s
m
m
s
m
m
¼
4
5
1
s
ðÞ5
s
ðÞ
s
m
m
where K
m
, m
m
are the dry-rock bulk and shear moduli, s
m
is the dry-rock electrical
conductivity, K
s
, m
s
,
s
are bulk modulus, shear modulus, and Poisson ratio for the
solid mineral, and s
s
is the electrical conductivity of the solid mineral.
431 9.5 Cross-property bounds and relations

For the case of a porous, “dry” rock (drained, pore-fluid bulk modulus ¼ 0)
consisting of an insulating solid mineral (
s
¼ 0) with porosity , filled with an
electrically conductive pore fluid of conductivity
f
6¼ 0, Berryman and Milton
(1988) obtained the following bounds relating the bulk and shear moduli ðK;Þ to
the electrical conductivity, , of the rock:
Berryman–Milton bounds
1
2
1
ðÞ
f
ðÞ
1
3K
4
s
1 K=K
s
ðÞ
1
2
1 ðÞ
f
ðÞ
21
5 21B
1 þ B
6A
1 ðÞ
s
A ¼
6 K
s
þ 2
s
ðÞ
2
3K
s
þ
s
ðÞ
2
B ¼
5
s
4K
s
þ 3
s
ðÞ
3K
s
þ
s
ðÞ
2
Gibiansky and Torquato (1996) obtained the following cross-property bound for a
dry, cracked rock with a finitely conducting solid mineral:
Gibiansky–Torquato bound
1
K
m
1
K
s
3
s
2
s
1
s
1 þ
s
1
m
1
s
Wet rocks
For fluid-saturated rocks with pore-fluid bulk modulus K
f
and pore-fluid conductivity
f
, such that K
f
=K
s
f
=
s
, Milton (1981) obtained the following inequalities for the
effective elastic moduli ðK;Þ and the effective electrical conductivity, :
Milton bounds
K
K
s
s
;
K
s
3
2
s
These inequalities remain valid when both K
f
¼ 0 and
f
¼ 0.
Combining Archie’s relation (see Section 9.4)
¼
f
m
where m is Archie’s cementation factor, with the Wyllie time-average relation (see
Section 7.3)
432 Electrical properties
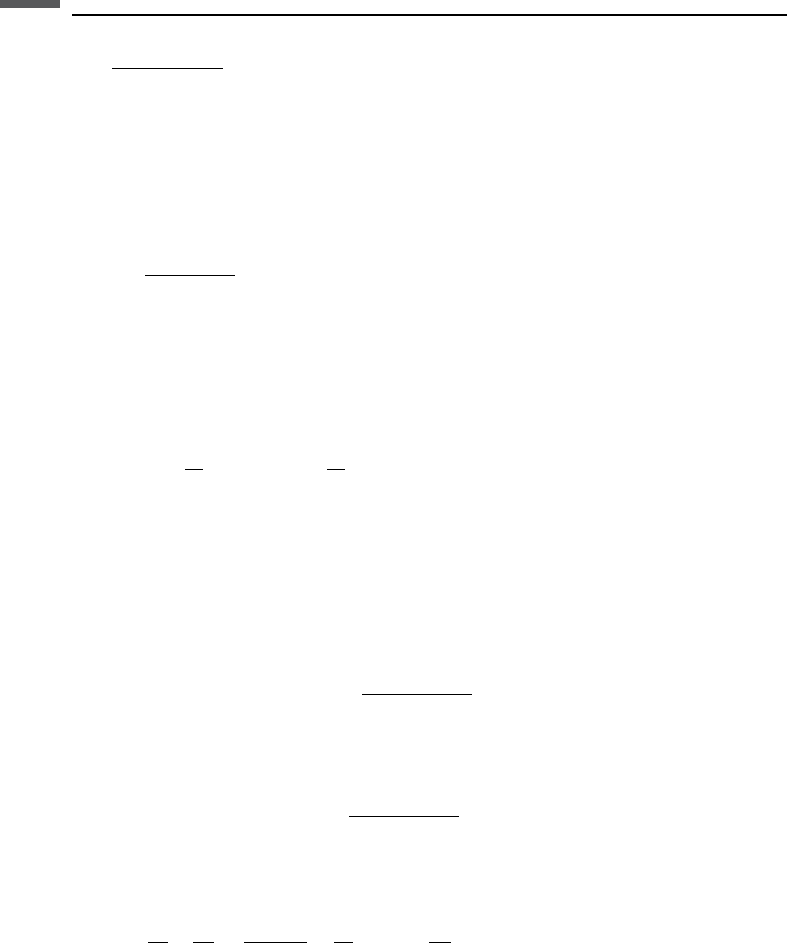
¼
1=V
P
1=V
0
1=V
f
1=V
0
where V
P
is the P-wave velocity in the porous rock, V
0
is the P-wave velocity in the
solid mineral grain, and V
f
is the wave velocity in the pore fluid gives the following
relation between bulk rock conductivity and elastic-wave velocity:
Archie/time-average
¼
f
V
0
=V
P
1
V
0
=V
f
1
m
Substituting porosity from Archie’s equation into the Raymer–Hunt–Gardner
velocity–porosity relation (see Section 7.4) gives:
Archie/Raymer
V
P
¼ 1
f
1=m
"#
2
V
0
þ
f
1=m
V
f
Similarly, solving for porosity from the Wyllie time-average equation and substitut-
ing into various conductivity–porosity relations gives the following cross-property
expressions (Carcione et al., 2007):
Glover et al. (2000)/time-average
¼ 1 ðÞ
p
s
þ
f
m
;¼
1=V
P
1=V
0
1=V
f
1=V
0
Hermance (1979)/time-average
¼
f
s
ðÞ
m
þ
s
;¼
1=V
P
1=V
0
1=V
f
1=V
0
Self-similar (Sen et al., 1981)/time-average
V
P
¼
1
V
f
1
V
0
s
s
f
f
11=m
þ
1
V
0
1
Brito Dos Santos et al. (1988) obtained the above relation combining the self-similar
conductivity model and the Wyllie time-average relation for elastic velocity, for a
porous medium with a conducting matrix. It should be noted that the results from the
Hermance (1979) and Glover et al. (2000) conductivity–porosity relations lie outside
the Hashin–Shtrikman bounds.
Raymer–Hunt–Gardner’s velocity–porosity relation combined with the Hashin–
Shtrikman lower bound on conductivity gives the following relation (Hacikoylu
et al., 2006):
433 9.5 Cross-property bounds and relations
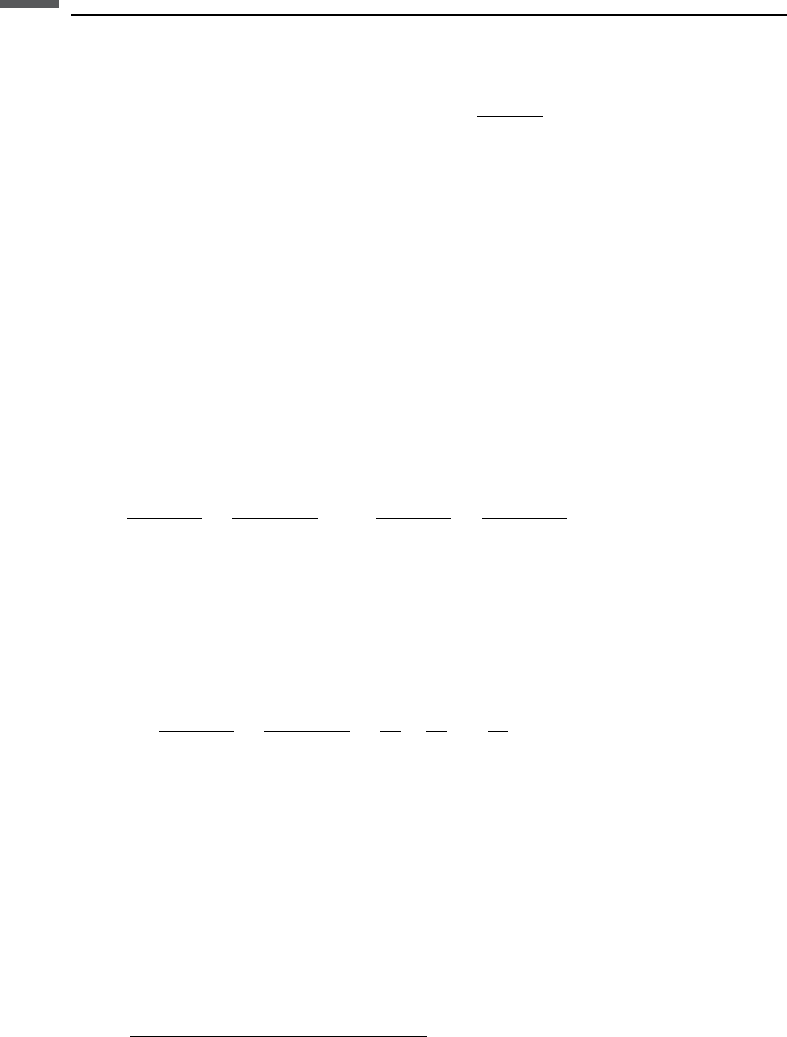
HS/Raymer
V
P
¼ 1 þ
p
2
V
0
þ
p
V
f
;¼
3
þ2
f
where
p
is the critical porosity (see Section 7.1), taken to be 0.4 in Hacikoylu et al.
(2006).
HS models
The Hashin–Shtrikman upper and lower bounds for electrical conductivity (see
Section 9.1 ) can be solved for porosity, which can then be inserted in the correspond-
ing Hashin–Shtrikman bounds for elastic moduli to obtain relations between elastic
and electrical properties. The porosity of a two-constituent composite, in terms of the
upper and lower Hashin–Shtrikman bounds on the electrical conductivity, is given as
follows (Carcione et al., 2007):
¼
s
HS
s
f
f
þ 2
s
HS
þ 2
s
¼
s
þ
HS
s
f
3
f
þ
HS
þ 2
f
where
þ
HS
and
HS
are the upper and lower Hashin–Shtrikman bounds for electrical
conductivity, respectively.
Carcione et al. substitute this porosity expression into the expression for the
Hashin–Shtrikman lower bound for the elastic bulk modulus, K
HS
, giving:
K
HS
¼
s
HS
s
f
f
þ 2
s
HS
þ 2
s
1
K
f
1
K
s
þ
1
K
s
1
Similar expressions can be obtained using the upper bound.
Gassmann-based relations
Carcione et al. (2007) suggest using Gassmann’s relation to derive relations between
elastic and electrical properties. Gassmann’s relation (see Section 6.3) relates the
elastic bulk modulus K
m
of a dry rock to the bulk modulus K
sat
of the same rock fully
saturated with a fluid of bulk modulus K
f
. One form of Gassmann’s relation is
K
sat
¼
K
s
K
m
ðÞþK
m
ðÞK
s
=K
f
1ðÞ
1 K
m
ðÞ=K
s
þ K
s
=K
f
For the dry bulk modulus, Carcione et al. suggest using a dry modulus–porosity
relation based on Krief’s equation (see Section 7.8):
K
m
¼K
s
1 ðÞ
1þAðÞ= 1ðÞ
434 Electrical properties
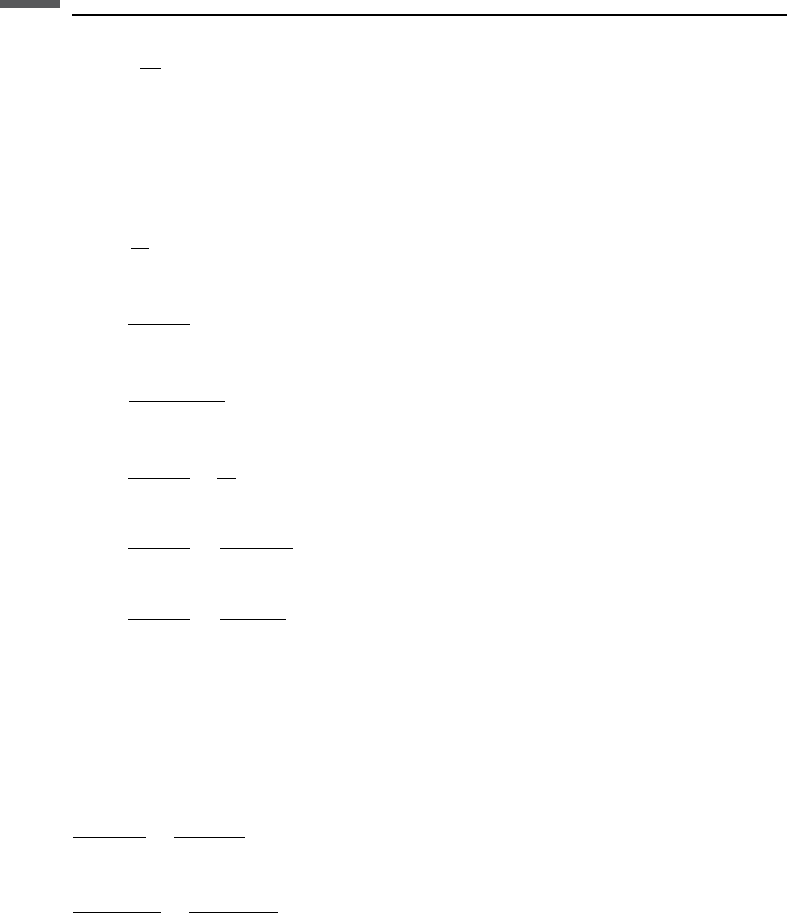
m
¼
s
K
s
K
m
Other K
m
-- models, such as the soft-sand or cemented-sand models described in
Section 5.4, can also be used. The porosity is then replaced by a porosity derived from
one of the many -- relations such as the following:
¼
f
1=m
Archie
¼
s
f
s
1=m
Hermance
¼
1=
1=
s
1=
f
1=
s
!
¼ 2 CRIM (see Section 9.3)
¼
s
f
s
f
11=m
self-similar
¼
s
s
f
f
þ 2
s
þ2
s
HS lower bound
¼
s
s
f
3
f
þ 2
f
HS upper bound
Layered media
By combining the Backus-averaged elastic modulus (see Section 4.13) and electrical
conductivity for a two-constituent layered medium with layering perpendicular to the
3-axis, Carcione et al. (2007) give the following relations:
11
2
1
2
¼
c
66
2
1
2
1
33
1
2
1
1
1
2
¼
c
1
44
1
2
1
1
1
2
Subscripts 1 and 2 denote the properties of the constituent layers, and the anisotropic
effective averaged quantities are denoted by the usual two-index notation.
Uses
These relations can be used to estimate seismic velocity from measured electrical
properties.
435 9.5 Cross-property bounds and relations

Assumptions and limitations
The empirical equations may not be valid for rock types and environments that are
different from the ones used to establish the relations. The Faust (1953) equation
may not be valid in soft, shaley sediment. The coefficient c in the Hacikoylu et al.
(2006) equation may have to be adjusted for environments other than the Gulf of
Mexico. When combining two relations for elastic and electric properties to obtain
a cross-property relation, the resulting equation will be a good description of the
cross-relation only if the original equations for elastic and electrical properties
themselves are good descriptors. These cross-relations have not been tested widely
with controlled data. Two of the empirical relations (Glover et al. and Hermance)
violate the theoretical Hashin–Shtrikman bounds.
436 Electrical properties
