Mench M.M. Fuel Cell Engines

Подождите немного. Документ загружается.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

260 Transport in Fuel Cell Systems

SOLUTION Based on Darcy’s law, the governing liquid transport equation in the porous

DM is expressed as

−k

∇P

where

= k

Here, k

, k

, and k are the liquid permeability, relative permeability, and absolute perme-

ability of the porous media. The capillary pressure in a hydrophobic diffusion media is

represented as

= P

− P

≈ const)

∇P

≈∇P

Using the Leverett function,

= γ cos θ





1/2

J (s

)

where for hydrophobic media

J (s

) = 1.417(s

) − 2.120(s

)

+ 1.263(s

)

Therefore, the capillary pressure gradient will become

∇P

≈∇P

= γ cos θ







At steady state, the mass ﬂux of liquid water going into the cathode DM is equal to the

amount of water generated in the catalyst layer due to the electrochemical reaction. Using

the mass balance on the control volume, the continuity equation for the liquid water inside

the DM is

where MW

is the molecular weight of the water and u

is given. Note that this also

assumes zero net transport through the electrolyte. Rearranging, the ﬁnal form of the

governing equation becomes

i · MW

· µ

2Fγ cos θρ

√

kφ

=−k

where k

= s

and



−

i · MW

· µ

2Fγ cos θρ

√

kφ

dx =





1.417s

− 4.24s

+ 3.78s



=−

0.35s

− 0.85s

+ 0.63s

i·MW

·µ

2F γ cos θρ

√

kφ

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.5 Multiphase Mass Transport in Channels and Porous Media 261

Inserting the values of the given properties along with the desired the local saturation values,

the corresponding locations will be

For s = 0.30 x

= 300 µm

For s = 0.25 x

= 200 µm

For s = 0.20 x

= 90 µm

COMMENT: This type of model is well suited for computational anaylsis.

5.5.5 Imbibition and Drainage Process

The process for wetting ﬂuid replacing nonwetting ﬂuid in a porous media is called im-

bibition. The opposite process is called drainage. A key relationship in capillary ﬂow is

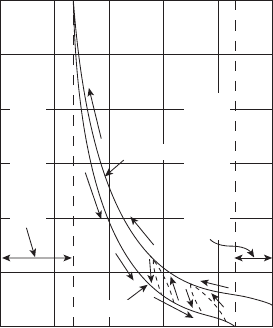
that relating the liquid saturation to the capillary pressure, which drives the motion of ﬂow.

Figure 5.36 shows a typical relationship P

= P

) during imbibition and drainage for

a porous medium. As shown s

nw,0

is the residual saturation of the nonwetting ﬂuid and

therefore limits the maximum saturation achievable with imbibition (condensation in the

pores can still ﬁll this residual fraction unless these pores are totally orphaned).

Point A on Figure 5.36 shows the bubbling (or breakthrough) pressure P

, which is

the minimum pressure needed to initiate displacement of wetting ﬂuid by nonwetting ﬂuid.

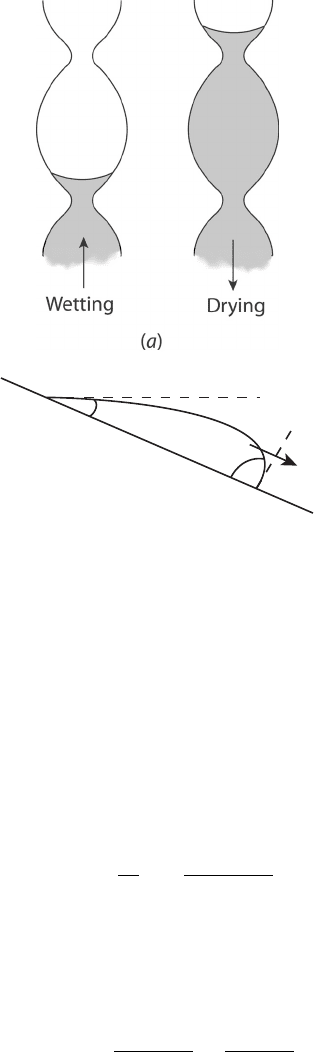
The hysteresis in porous media observed between imbibition and drainage is a result of

several effects, including the so-called ink-bottle and rain drop effect, as shown in Figure

5.37. In the ink-bottle effect, as liquid enters a widening pore, the capillary forces change

with the increasing diameter, which can trap a droplet. The rain drop effect is a result of

(%)

100806040200

100 80 60 40 20 0

NWO

Capillary pressure

Irreducible wetting

fluid saturation (s

)

Residual saturation of

nonwetting fluid (s

)

Drainage

Inbibition

Figure 5.36 Typical wetting/drying curves for porous media illustrating hysteresis. (Reproduced

from [41].)

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

262 Transport in Fuel Cell Systems

(b)

Figure 5.37 Illustration of hysteresis effects: (a) ink bottle effect; (b) rain drop effect. (Reproduced

from [41].)

gravity on nonhorizontal surfaces and can result in asymmetric droplet shape and capillary

forces.

5.5.6 Phase Change in Porous Media: Capillary Condensation

In very small pores, gas-phase pressure increases according to the Kelvin equation:

T ln





2γ

V cos θ

(5.105)

where P

is the increased pore vapor pressure, P

is the bulk vapor pressure,

V is the molar

gas volume, γ is the surface tension of the liquid surface, and r is the radius of curvature

of the liquid. Recalling the deﬁnition of relative humidity from Chapter 3,

RH = φ =

Total

g,sat

(T )

vapor

g,sat

(T )

(5.106)

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.6 Heat Generation and Transport 263

So as P

tot

increased, the RH increases, y

decreases, and condensation occurs in pores above

the normal bulk condensation temperature due to increased pore-level vapor pressure. This

is not a signiﬁcant effect in most fuel cells and does not matter for any species besides

water. For example, for a 50-nm (typical of a catalyst layer) pore at 80

◦

C, water will

condense at approximately 100.5

◦

C. So capillary condensation is not a major effect in DM

or catalyst layers but can be signiﬁcant for vapor dissolving and condensing into solid

polymer electrolytes with nanometer-size holes.

5.6 HEAT GENERATION AND TRANSPORT

5.6.1 Heat Generation

In an operating fuel cell, even though the efﬁciency may be higher than a conventional

combustion engine, there is still a considerable amount of the initial chemical energy

dissipated as heat through operation. For a 50% efﬁcient 100-kW engine, 100 kW still

needs to be dissipated as heat. For high-temperature systems, such as the SOFC, the heat

dissipation is not a major issue; in fact, the waste heat is high quality, because it can easily

be used for some other purpose to raise the effective efﬁciency of the overall process, such

as to convert water to steam and run a turbine or to heat a building. The process of using

waste heat for another purpose is termed cogeneration and is explored in the Application

Study at the end of this chapter. In high-temperature systems such as the MCFC and SOFC,

fuel cell warm-up and maintaining a steady elevated temperature for operation are also

important issues. Some dissipation can be achived using the reactant gas. For fuel cell

systems with recirculating liquid electrolyte, signiﬁcant cooling can be achieved through

the electrolyte. Other large fuel cell systems usually require active coolant recirculation

control systems. For low-temperature PEFC systems, heat rejection is challenging for the

following reasons:

1. In a typical combustion engine, around 80% of the waste heat is removed by the

exhaust gas ﬂow. In a larger PEFC stack, the waste heat is primarily removed by

the fuel cell coolant, and relatively little heat is removed by the exhaust ﬂow. This

puts additional heat rejection burdens on the system.

2. Due to the low operating temperature, the heat rejection rate to the environment is

reduced compared to a combustion engine, since the heat transfer rate is proportional

to the temperature difference between the heated source and the ambient.

In Chapter 4, the heat generation ﬂux in a fuel cell was shown to be related to the current

and the departure of the cell voltage from the thermal voltage:



heat

(W/cm

) = i(E

− E

cell

) (5.107)

where i is the operating current density, E

is the thermal voltage, and E

cell

is the fuel

cell operating voltage. The cell voltage is of course a function of activation, ohmic, and

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

264 Transport in Fuel Cell Systems

concentration polarizations. This heat generation includes the reversible heat generated by

the entropy change, which is the difference in the thermal and Nernst voltages:



heat,rev

(W/cm

) = i(E

− E

◦

) = i



−

H

−

G



=−i

T S

(5.108)

This entropy-generated heat is known as Peltier heating. The irreversible heat generated

by activation, ohmic, and concentration polarizations is



heat,irr

(W/cm

) = i(E

◦

− E

cell

) = i(η

a,a

+|η

a,c

|+η

m,a

+|η

m,c

|+η

+ η

) (5.109)

where the various polarizations are deﬁned in Chapter 4. The total heat generated by reaction

polarizations is the sum of the reversible and irreversible components:



total

(W/cm

) =−i

T S

+ i(η

a,a

+|η

a,c

|+η

m,a

+|η

m,c

|+η

+ η

) (5.110)

As current density increases (corresponding also to reduced cell voltage), the thermal energy

dissipation ﬂux will increase. The ﬁrst term on the right-hand side of Eq. (5.110) represents

Peltier heating. The second term on the right-hand side represents the sum of the activation

(kinetic), concentration, ohmic, and crossover contributions to the heat generation.

5.6.2 Single-Phase Heat Transport

Conduction Conduction is heat transfer resulting from intermolecular collisions. At a

molecular level, as a molecule with higher thermal energy collides with a molecule with

lower thermal energy, some of the energy is transferred to the lower energy system. The gov-

erning equation for conduction heat transfer is known as Fourier’s law of heat conduction,

which is analogous to Fick’s law of mass diffusion, written in three dimensions as



heat,i

(W/m

) =−k

∂T

∂x

(5.111)

where subscript i represents the x, y,orz dimension, k

is the thermal conductivity in the

i direction, and q



heat,i

is the conduction heat transfer ﬂux in the i direction. Expanded into

three dimensions, Eq. (5.111) is written as



heat,x

=−k

∂T

∂x



heat,y

=−k

∂T

∂y



heat,z

=−k

∂T

∂z

(5.112)

In many cases, the thermal conductivity is isotropic and therefore not a function of

orientation. However, for some fuel cell materials, the value should be highly anisotropic

based on structure and material orientation. An example of this is the woven diffusion media

structure of the PEFC shown in Figure 5.38. The layered woven pattern should result in a

much higher in-plane electrical and thermal conductivity than the through-plane direction.

The thermal conductivity of many PEFC materials has been measured as a function

of compression pressure and temperature [49]. Representative values of PEFC material

It is assumed the reader has a cursory knowledge of basic heat transfer. The reader is referred to other texts for

additional information, such as Fundamentals of Heat and Mass Transfer, 5th ed., by F. P. Incropera and D. P.

DeWitt, Wiley, New York, 2002.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.6 Heat Generation and Transport 265

Figure 5.38 Cross-sectional SEM of membrane electrode assembly, microporous layer, and paper-

based macro diffusion media.

conductivity and other fuel cell material conductivity are given in Tables 5.14 and 5.15,

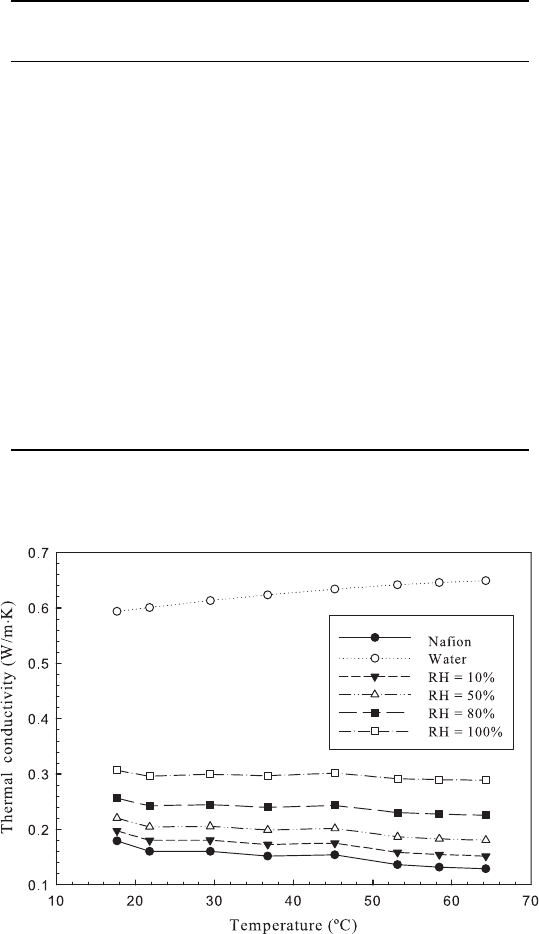
respectively. A plot of the estimated thermal conductivity of Naﬁon electrolyte with water

content is shown in Figure 5.39.

For solids, the thermal conductivity is a combination of the transport of free electrons

and vibration of bound lattice atoms [50]:

= k

+ k

(5.113)

Table 5.14 Measured Thermal Conductivity of Polymer Electrolyte Fuel Cell Components.

Measured k

Material (W/m · K)

DuPont Naﬁon membrane (at 30

◦

C) 0.16 ± 0.03

W. L. Gore reinforced electrolyte 0.16 ± 0.03

Toray carbon ﬁbar paper diffusion media (TGP-H at 57

◦

C) 1.76 ± 0.30

SIGRACET 0 wt % PTFE carbon-ﬁber paper diffusion media (AA series at 56

◦

C) 0.48 ± 0.09

SIGRACET 5 wt % PTFE carbon-ﬁber paper diffusion media (BA series at 58

◦

C) 0.31 ± 0.06

SIGRACET 20 wt % PTFE carbon-ﬁber paper diffusion media (DA series 58

◦

C) 0.22 ± 0.04

E-Tek ELAT carbon cloth diffusion media (LT1200-W at 33

◦

C) 0.22

± 0.04

Catalyst layer (0.5 mg/cm

platinum on carbon) 0.27

± 0.05

Effective thermal conductivity (includes thermal contact resistance with diffusion media)

Source: From [49].

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

266 Transport in Fuel Cell Systems

Table 5.15 Thermal Conductivity of Fuel Cell Components

Thermal Conductivity

Material (W/m · K) @25

◦

Platinum 70

Nickel 91

7% YSZ (SOFC electrolyte) ∼2.0 [56]

Pure Graphite ∼90

Stainless steel 16

Aluminum Oxide 30

Aluminum 250

Carbon 1.7

Steel 46

Teﬂon

0.25

Fiberglass 0.04

Oxygen 0.024

Nitrogen 0.024

Hydrogen 0.17

Water vapor 0.016

Liquid water 0.58

Methanol 0.21

Figure 5.39 Estimated thermal conductivity of Naﬁon 1100 EW at different humidity ratios. The

thermal conductivity variation of pure water is shown as an upper bound for the theoretical moist

Naﬁon thermal conductivity [49].

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.6 Heat Generation and Transport 267

For electrical conductors such as metals, the electron conductivity portion dominates, and

the thermal and electrical resistances can be correlated by the Wiedemann–Franz law:

= LT (5.114)

where T is the absolute temperature, k

is the thermal conductivity, σ

is the electrical

conductivity, and L is the proportionality constant known as the Lorenz number, determined

from quantum mechanics to be

L = 2.45 × 10

−8

W · /K

(5.115)

This result matches with experiment quite well for most metals above room temperature. For

electrical insulators, however, such as electrolytes, the lattice vibration thermal conductivity

dominates, and the more ordered and crystalline the structure is, the greater the thermal

conductivity. For these materials, Eq. (5.114) does not hold true.

For gases, the thermal conductivity generally increases with temperature. For fuel cells,

it is noteworthy that the thermal conductivity of hydrogen is about 5–10 times greater than

for air or water vapor. As a result, a greater fraction of the heat is transported through anode

than through cathode ﬂow, although the total transported by gas ﬂow is much less than by

direct conduction of heat through the lands.

Convection: Internal Correlations and Deﬁnitions Mass and heat transport in fuel cells

is not only by diffusion and conduction. There are numerous instances where mass and

heat transport by convection is important, most notably in fuel cell ﬂow channels or in fuel

cells with recirculating electrolytes. Fundamentally, convection is a result of the motion of

the ﬂuid ﬁeld. It should be noted that diffusion itself necessarily induces motion and thus

convection, but this is accounted for in the diffusion ﬂux. What we are talking about in

this case is transport via motion of the bulk ﬂow ﬁeld. As an example, consider a stagnant

glass of clear water in which a droplet of food coloring is placed. Slowly, the color diffuses

through the water (by measuring the rate of radial transport in a static environment you

can measure the diffusion coefﬁcient). Now, consider stirring the same glass as the food

coloring is added. Obviously, the mixing will occur more quickly. This is a result of the

motion of the general ﬂuid ﬁeld. Convection transport can be modeled with a convective

mass transport coefﬁcient:





mol

· s



= h

− C

) (5.116)

where



is the molar ﬂux of the species, h

is a convective mass transfer coefﬁcient and C

and C

are the surface and mean concentrations, respectively. The mass transfer coefﬁcient

is analogous to the heat transfer convection coefﬁcient and is known for various geome-

tries and ﬂow regimes as shown in many undergraduate heat and mass transfer textbooks

[e.g., 50].

At the fundamental level, heat transfer into a ﬂuid is through conduction at the boundary

of the interface, as shown in Figure 5.40. Within the ﬂow, random molecular motion and

Recall that the lands are the portion of the ﬂow ﬁeld that contacts the diffusion media/catalyst layer, providing

direct contact for electrical and thermal conduction.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

268 Transport in Fuel Cell Systems

T high

Convective

heat flux

q˝

=−

∂

Figure 5.40 Schematic of ﬂuid ﬂowing over heated interface showing local conduction at interface

and advection of heat through boundary layer. The sum of the molecular-level interaction conduction

and heat transfer by bulk motion (advection) is terms the convection heat transfer.

collisions still occur, resulting in conduction heat transfer. In a moving ﬂuid, however, there

is also heat transfer by the bulk motion of the ﬂow, termed advection, that can dominate the

transport of heat. The combination of conduction and advection is known as convection.

To illustrate this, think of a cold pot of water on a heated stove. The water near the bottom

of the pot will be heated ﬁrst, and the heat will conduct to the top of the water, which is a

relatively slow process (ignoring natural convection effects). To hasten the heat transfer, a

simple stir of the water will bring the heated water from the bottom of the pot to a location

near the top, adjacent to the cold water, heating the cold water by intermolecular collision.

There are two main classiﬁcations of convection, forced and natural. Forced convection

is ﬂuid motion that is a result of forced input, such as a fan or pump. Natural convection is

a result of density gradients in the ﬂow which cause motion. In forced convection, there is

also often a component of natural convection, but this is typically dominated by the forced

convection effects. The density gradients in the ﬂow, which are the genesis of natural

convection, can be caused by either temperature or solutal buoyancy effects. Temperature

effects are simply a result of the density–temperature relationship for a ﬂuid. These effects

can be illustrated by imagining a window in a warm apartment on a cold winter day (see

Figure 5.41). At the inside surface of the window, the air in the room is cooled by the window

and increases in density, sinks down along the window, and causes an uncomfortable draft.

Solutal buoyancy forces are the result of the mixture changing its distribution of species

and its density. For example, in a portable fuel cell, dry air is brought in from the ambient,

and oxygen is consumed, while the mixture is simultaneously heated and humidiﬁed, as

shown in Figure 5.42. The uptake of water (MW 18 g/mol) into a mixture of air (MW 28.85)

Window

Outside

(cold)

Inside

(warm)

Local cooling air

sinks, causing motion

Figure 5.41 Schematic of natural convection ﬂowing from a cold window.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.6 Heat Generation and Transport 269

Heat

into Air

Moisture

into Air

Increasing Temperature

Buoyancy Force

Decreasing Molecular Weight

Buoyancy Force

Dry Air Flow In

Figure 5.42 Schematic of thermal and solutal natural convection.

reduces the molecular weight and density of the mixture, which induces a solutal buoyancy

convection motion in the ﬂow in addition to any thermal or forced effects.

Despite the relative complexity of convective heat transfer, it is often modeled with a

bulk heat transfer coefﬁcient h. The heat ﬂux from a surface at temperature s to a ﬂuid at

temperature m is written as



heat

(W/m

) = h(T

− T

) (5.117)

where q



heat

is the local heat ﬂux, h is the local convective coefﬁcient, T

is the surface

temperature of the enclosure in contact with the ﬂuid, and T

is an appropriate mean

temperature of the ﬂuid. The mean temperature in a ﬂow channel can be solved analytically

from the following relationship [50]:



ρuc

TdA

(5.118)

where T

is the mean temperature difference of the ﬂuid throughout the length of the ﬂow

channel. Here, A

is the cross-sectional area, c

is the constant volume speciﬁc heat of the

ﬂuid,

m is the bulk mass ﬂow rate of the ﬂuid, and u is the velocity proﬁle in the ﬂuid.

Note that all of these properties can in principle vary in distance along the ﬂow channel.

In thermally fully developed ﬂow with constant speciﬁc heat, the heat transfer coefﬁcient

can be shown to be independent of axial location. From an energy balance on the enclosed

channel, it can be shown that



heat

(

− T

)

(5.119)

where P is the perimeter of the enclosed channel (2 ×width + 2 × height for a rectangular

channel). For a constant surface heat ﬂux condition, we can show from Eq. (5.119), that

(x) = T

m,i



heat

x (5.120)