Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.

432 9 Predictive Control
−1 −0.5 0 0.5 1
−1
−0.5
0
0.5
1
x
1
x
2
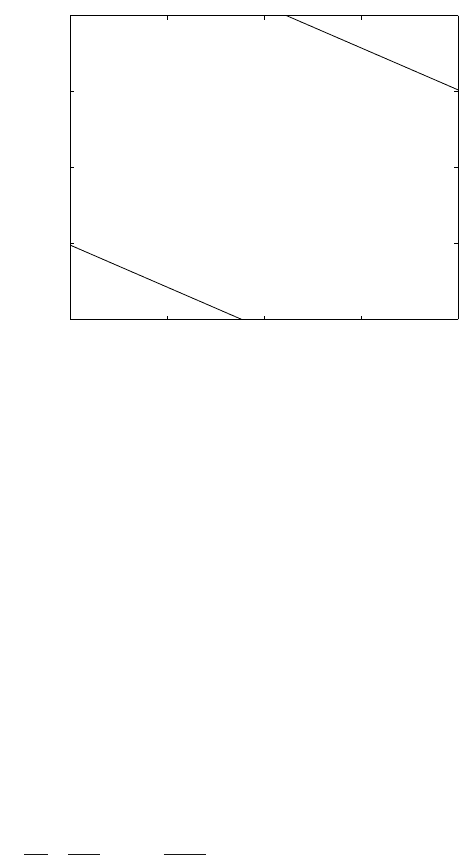
u = −0.52 x
1
−0.94 x
2
u = −1
u = 1
Fig. 9.3. Controller regions and the optimal control for the double integrator
example
2. If the sampling time has not yet been specified, select it as the larger value
that satisfies
T
s
≤ 0.1T, T
s
≤ 0.5T
d
(9.124)
3. Calculate the discrete dead time
¯
T
d
(rounded to the next integer)
¯
T
d
= T
d
/T
s
+ 1 (9.125)
4. Set N
1
=1,and
N
2
=5T/T
s
+
¯
T
d
(9.126)
5. Select the control horizon N
u
(usually between 1–6) and calculate the
control weighting λ as
f =
$
0 N
u
=1
N
u
500
3.5T
T
s
+2−
N
u
−1
2
N
u
> 1
(9.127)
λ = fZ
2
(9.128)
9.7.2 Multivariable Tuning based on the First Order Model
This tuning strategy is a generalisation of the previous approach to multivari-
able systems with R outputs and S inputs. Again, it is based on the analysis
of the first order system with time delay.
9.7 Tuning 433
1. Approximate the process dynamics of all controller output-process vari-
able pairs with first order plus dead time models:
y
r
(s)
u
s
(s)
=
Z
rs
T
rs
s +1
e
−T
d,rs
s
(9.129)
2. Select the sampling time as close as possible to:
T
s
rs
= max(0.1T
rs
, 0.5T
d,rs
),T
s
= min(T
s
rs
) (9.130)
3. Set N
1
= 1, compute the prediction horizon N
2
:
N
2
= max
5T
rs
T
s
+ k
rs
,k
rs
=
T
d,rs
T
s
+ 1 (9.131)
4. Select a control horizon N
u
, equal to 63.2% of the settling time of the
slowest sub-process in the multivariable system:
N
u
= max
T
rs
T
s
+ k
rs
(9.132)
5. Select the controlled variable weights γ
r
, to scale process variable mea-
surements to similar magnitudes
6. Compute the control weightings λ
s
as
λ
s
=
M
500
R
r=1
γ
r
Z
2
rs
N
2
− k
rs
−
3
2
T
rs
T
s
+2−
M − 1
2
(9.133)
Fine tuning of the method is performed by increasing the corresponding γ
r
of the process variable for which tighter control is desired and increasing the
corresponding λ
s
of the manipulated variable for which less aggressive moves
are desired.
9.7.3 Output Horizon Tuning
This tuning strategy assumes the active tuning parameter to be the output
horizon N
2
with all other fixed at the values
N
1
=1,N
u
=1,P=1,λ= 0 (9.134)
It is well known that if N
2
→∞, mean-level controller results. This controller
is rather conservative as its speed is the same as step responses.
The other limit for N
2
is the value of the process dead time. If N
2
= T
d
+1,
where T
d
represents process dead time, then we have the Minimum Variance
(MV) controller known to be unstable for non-minimum phase plants.
The practical range for N
2
can be specified as
T
d
+1<N
2
≤ T
90
/T
s
(9.135)

434 9 Predictive Control
where T
90
is the time when process reaches about 90% of its final value after
input step change and T
s
is the sampling time.
If the process is uncertain, it is better to start with a larger value of N
2
.
The minimum value of N
2
for non-minimum phase plants should be such that
*
i
g
i
has the same sign as the process gain.
9.7.4 λ Tuning
In this case the active tuning parameter is the penalisation of control moves
λ. All other parameters are fixed as
N
1
= deg(B)+1,N
u
= deg(A)+1,N
2
≥ N
u
+ N
1
− 1 ≈ t
r
/T
s
,P=1
(9.136)
With λ equal to zero, dead-beat controller results. This is too rapid in the
majority of cases. Hence, with increasing value of λ the controller is made
more conservative. It might be shown that the closed-loop poles converge to
the open loop poles if λ →∞.Thusλ tuning is not recommended for unstable
plants.
It has been found that to desensitise the closed-loop system to changes in
process dynamics, the actual λ should be proportional to B(1)
2
:
λ = λ
0
B(1)
2
(9.137)
with λ
0
being a constant.
To determine a starting value of λ, the following relation can be used:
λ =
m tr(G
T
G)
N
u
(9.138)
and m is a factor of detuning the controller relative to the dead-beat control.
The control increments are approximately reduced by a factor m+1 compared
to that of the dead-beat strategy.
From this starting value of λ, an initial guess for λ
0
can be determined
from (9.137).
9.7.5 Tuning based on Model Following
As it has been shown before, the P polynomial can be used to generate ref-
erence trajectory w/P. GPC can be set up to follow this trajectory exactly
and so to place the closed-loop poles at the process zeros. In order to have a
more practical controller, the model following can be detuned. This may be
accomplished by either increasing N
2
or λ.
The fixed parameters are as follows:
N
1
=1,N
u
= deg(A)+1,N
2
≥ N
u
+ T
d
≈ t
r
/T
s
,λ= 0 (9.139)

9.7 Tuning 435
Most often, the models M =1/P are of the first and the second order. If
the first order closed-loop model is assumed to be of the form
M(s)=
1
Ts+1
(9.140)
then its discrete equivalent is
M(z
−1
)=
(1 −p
1
)z
−1
1 −p
1
z
−1
(9.141)
where p
1
=exp(−T
s
/T ). The polynomial P can thus be chosen as (cf. equa-
tion (9.12)) and P (1) is equal to 1 to ensure the offset-free behaviour. This
model is applicable mainly for simpler plants as the first order trajectory may
sometimes generate excessive control actions.
The second order model can be of the form
M(s)=
1
T
2
s
2
+2Tζs+1
(9.142)
Its discrete time equivalent is
M(z
−1
)=
n
1
z
−1
+ n
2
z
−2
1+p
1
z
−1
+ p
2
z
−2
(9.143)
where
p
1
= −2exp
−ζT
s
T
cos
T
s
T
1 −ζ
2
(9.144)
p
2
=exp
−2ζT
s
T
(9.145)
Ignoring the numerator dynamics, the polynomial P may be specified as
P (z
−1
)=
1+p
1
z
−1
+ p
2
z
−2
1+p
1
+ p
2
(9.146)
The dominant time constant of the closed-loop system is approximately 2T
and the fractional overshoot is solely a function of the damping factor ζ:
o
v
=exp
-
−πζ
1 −ζ
2
.
(9.147)
and thus the user can then specify the desired rise time and overshoot and
translate these settings into an appropriate P polynomial.
9.7.6 The C polynomial
The CARIMA model includes knowledge about the disturbance properties in
the polynomial C. This can be estimated on-line using a suitable recursive

436 9 Predictive Control
identification algorithm. However, this is rather difficult in practice, because
the convergence of the C polynomial coefficients is rather slow.
Therefore, a more realistic approach is to set C by user directly. The value
that has been suggested as a default in the literature is of the form
C =(1− 0.8z
−1
)
2
(9.148)
Another possibility that follows from the optimal LQ theory is to calcu-
late it as a stable polynomial from spectral factorisation of the denominator
polynomial A as
C
∗
C = A
∗
A (9.149)
9.8 Examples
In this section some examples of the GPC control algorithm are shown. The
first example shows some effects of the tuning parameters that have been
described in the previous sections.
The bioreactor control example demonstrates the possibility of using a
non-linear model for predictions. Here, an artificial neural network model is
used. Comparison with an adaptive control based on a linear model shows
some drawbacks of adaptive methods applied to non-linear processes.
Finally, the pH control example shows a real-time control problem. It is
demonstrated that GPC is able to control such a strong non-linear process.
9.8.1 A Linear Process
Let us consider a linear continuous-time system with transfer function
G(s)=
1
(s +1)
2
(9.150)
that is discretised with the sampling time T
s
=1.
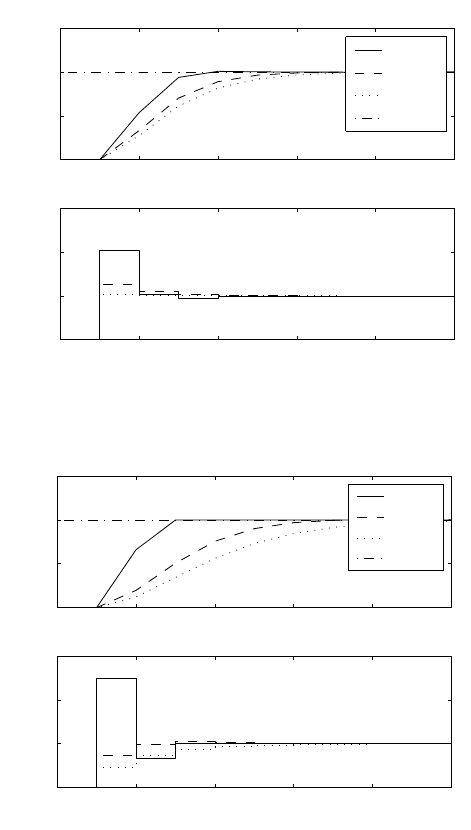
Two simulation runs were performed. In the first, mean level settings were
given. The GPC parameters were N
1
=1,N
u
=1,λ =0,andN
2
varied
between 2 − 20. The results are shown in Fig. 9.4 and illustrate that with
the increasing N
2
the control actions are smoother, more conservative and
converge to input step change.
In the second simulation λ was given as the varying parameter. The set-
tings of other parameters were N
1
=3,N
u
=3,N
2
= 5 which for λ = 0 gives
the dead-beat controller. Increasing λ gives more weight to control increments
and slows down the controller. The results are shown in Fig. 9.5.
9.8 Examples 437
0 2 4 6 8 10
0
0.5
1
1.5
Output
y,w
N
2
=2
N
2
=5
N
2
=20
w
0 2 4 6 8 10
0
1
2
3
Control
sam
p
le
u
Fig. 9.4. Increasing value of N
2
leads towards mean-level control
0 2 4 6 8 10
0
0.5
1
1.5
Output
y,w
λ=0.0
λ=0.1
λ=1.0
w
0 2 4 6 8 10
0
1
2
3
Control
sample
u
Fig. 9.5. Increasing value of λ - detuned dead-beat control

438 9 Predictive Control
9.8.2 Neural Network based GPC
In this example we compare an adaptive GPC based on linear model (AGPC)
and implemented in the same way as in the previous example to GPC based
on non-linear neural network model (GPCNN).
The process studied was the bioprocess that describes the growth of Sac-
charomyces cerevisiae on glucose. The oxygen concentration c
o
and the dilu-
tion rate D
g
have been selected as the controlled and the manipulated vari-
ables, respectively.
A feedforward ANN plant model with the third order input dynamics and
one hidden layer was used. This means six neurons in the input layer with
signals
y(k − 1),y(k − 2),y(k − 3),u(k − 1),u(k − 2),u(k − 3) (9.151)
For the calculation of the step response, the ANN inputs are
y(k − 1),y(k − 1),y(k − 1),u
n
,u(k − 1),u(k −1) (9.152)
where the step change magnitude u
n
was specified as
u
n
= u(k − 1) +
w − y(k − 1)
Z
(9.153)
and the process static gain Z was determined from the step response estimated
in the previous sampling period. The static gain Z was initially set equal to
1. To take into account the fact that the initial conditions are not equal to
zero and the step input is not of unit value, the ANN approximation of the
step response is subsequently normalised.
For the free response the ANN inputs are
u(k − 1),u(k − 2),u(k − 3),y(k − 1),y(k − 2),y(k −3) (9.154)
and it is assumed that the input is constant in the future.
The sampling period was set equal to 0.5 h. The training and validation
data sets (800 input-output pair samples) were obtained using a pseudo ran-
dom binary sequence input. The conjugate gradients algorithm was used as a
learning method and a genetic algorithm was used for the initialization of the
ANN weights.
For the AGPC, a third order discrete model has been considered for process
modelling. The model parameters have been estimated using the parameters
estimation algorithm LDDIF.
The GPC parameters were N
1
=1,N
2
=14,N
u
=4,λ =0.1. The ob-
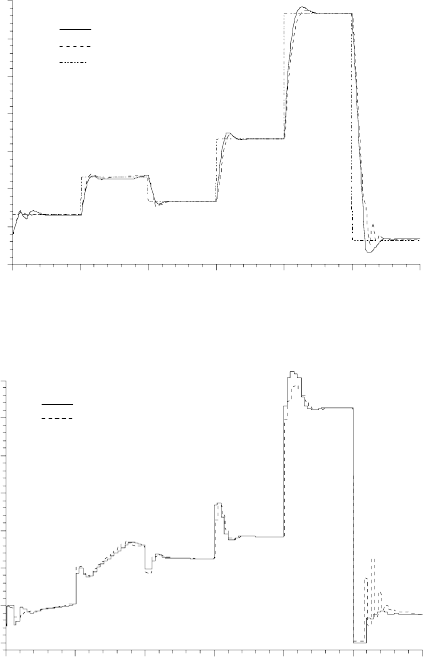
tained profiles of the process output controlled by the AGPC (dashed line)
and the GPCNN (solid line) are shown in Fig. 9.6. Figure 9.7 shows the pro-
files of the control actions generated by AGPC (dashed line) and GPCNN
(solid line), respectively. As it can be seen from these figures, both algorithms
9.8 Examples 439
0 102030405060
0,0
0,3
0,6
0,9
1,2
1,5
1,8
2,1
c
o
- GPCNN
c
o
- AGPC
w
c
o
. 10
5
[ mol / l ]
Time [ h ]
Fig. 9.6. Trajectories of the oxygen concentration (the process output)
0 102030405060
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
Dg - GPCNN
Dg - AGPC
Control action Dg [1/h]
Time [ h ]
Fig. 9.7. Trajectories of the dilution rate (the manipulated variable)
achieve good results. When a large change of the setpoint occurs (see Fig. 9.7,
t = 50 h), GPC based on linear model leads to a generation of a bad transient
behaviour. Unlike AGPC, GPC based on ANN generates a smooth control
action which leads to a good control behaviour. This behaviour was expected
as the AGPC is based on linear model. Due to the nonlinear characteristic of
the bioprocess, a large change of the setpoint or some disturbance can bring
the process into other operating points with different dynamical properties.
9.8.3 pH Control
The experimental pH control has been studied at the University of Dortmund.
440 9 Predictive Control
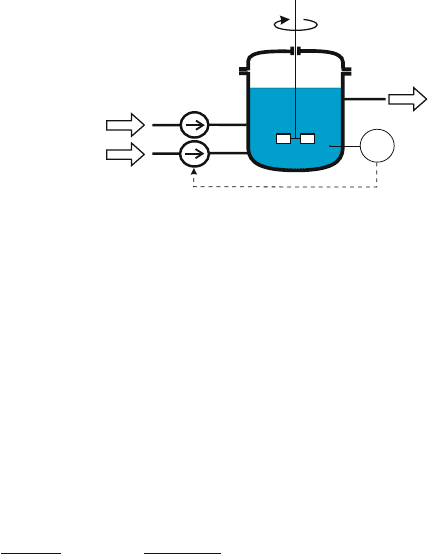
The neutralisation plant to be controlled consists of a laboratory-scale
continuous stirred tank with two inlets and one outlet (see Fig. 9.8)), in which
acetic acid is neutralized with sodium hydroxide.
The hold-up of the tank is 5.57 l, the concentrations of the acid and the
sodium hydroxide solution streams are approximately 0.01 mol/l. The acid
flow rate F
A
is fixed at 0.33 l min
−1
, whereas the NaOH flow F
B
is manipulated
by the controller. In order to obtain the necessary precision of the flow rates
diaphragm pumps were chosen. All control actions are performed by a PC-
based control system. The flow F
B
is controlled by the modulation of an
impulse frequency f, which leads to a quantisation of the control amplitude
because the frequency can assume only certain discrete values.
acetic acid
sodium
hydroxide
efluent
stream
QIC
pH
Fig. 9.8. Neutralisation plant
In the tank, the following reaction takes place:
NaOH + CH
3
COOH CH
3
COONa + H
2
O (9.155)
Due to the incomplete dissociation of the acetic acid in water and the
equilibrium reaction with sodium hydroxide the system behaves like a buffer
solution between pH 4 and 6.5. Consequently, the process gain varies extremely
over the range of pH-values that can be controlled.
The controlled variable pH and the control variable F
B
have been scaled
for control and identification purposes as
y =
pH −7
7
u =
F
B
− F
s
B
F
s
B
(9.156)
where F
s
B
denotes the approximate steady state value of F
B
corresponding to
pH = 7.
The parameters for the GPC controller were chosen as N =50,N
u
=
4,λ =1,α =0.3. Several model orders have been tried, the best results have
been obtained with the third order model. The sampling time was set at 5s.
The tuning of the predictive algorithm was performed at pH = 9 with
the requirement, that the deviations from the steady-state have to be within
9.8 Examples 441
±0.1pH. It was observed, that the small values of N
u
led to rather active con-
trol actions and the final value N
u
= 4 was chosen as the result of trade-off
between the performance and the complexity of the calculations. The param-
eter λ influenced the penalisation of the future control increments. Very large
values caused limit cycles of pH as the control was unable to compensate sat-
isfactorily the disturbances, therefore the smallest possible value was chosen.
For the final tuning of the algorithm, the P polynomial was used. Only
the first order polynomial of the form P (z
−1
)=(1− αz
−1
)/(1 − α)was
assumed. The smaller values resulted in increased steady-state deviations and
the larger values in very slow and oscillatory response to setpoint changes.
The value α =0.3 was chosen as a compromise.
The experimental results of the adaptive GPC controller were compared
with a carefully tuned PI controller. All experiments were carried out with the
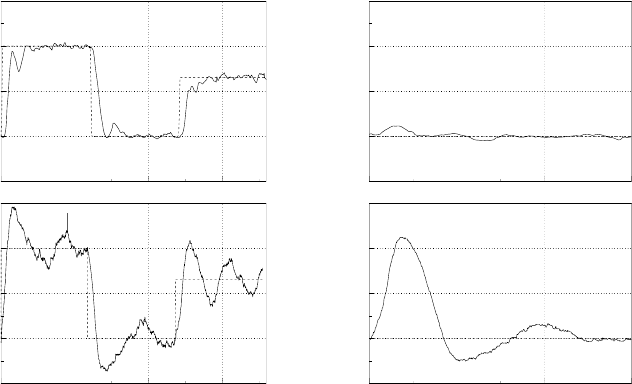
same pattern of setpoint changes. At first the reactor was stabilised at pH = 7
and then controlled to pH = 9, 7, 8.3 (Fig. 9.9). Finally, the disturbance
rejection performance has been studied. As a disturbance, a 20% decrease
of the acid flow was performed at t = 0 and held constant afterwards (see
Fig. 9.10).
0 500 1000 1500
6
7
8
9
10
PI controller
pH [ ]
Time [s]
6
7
8
9
10
GPC controller
pH [ ]
Fig. 9.9. Setpoint tracking
0 200 400 600
6
7
8
9
10
PI controller
pH [ ]
Time [s]
6
7
8
9
10
GPC controller
pH [ ]
Fig. 9.10. Disturbance rejection
The experiments have confirmed, that the adaptive GPC method is able to
control the strongly nonlinear plant and that it behaves much better compared
to the linear PI control. However the tuning of the controller parameters
must have been done with some care and only the parameters which slowed
