Мирошник И.В. Теория автоматического управления. Линейные системы
Подождите немного. Документ загружается.

290
Глава
9.
Цифровые
системы
управления
и
отражает
основное
свойство
этого
блока
как
квантователя
аналоговых
сиг
налов,
обусловленное
циклическим
характером
работы
АЦП
или
периодическим
обращением
центрального
процесса
к
буферному
регистру.
При
необходимости
в
состав
устройств
ввода
включаются
также
реверсивные
счетчики,
осуществляющие
преобразование
последовательного
кода
n
у
В
парал
лельный
код
N'JJ
(см.
рис.
9.4).
Устройства
вывода
информации
обеспечивают
временное
хранение
и
преобразова
ние
информации,
полученной
от
ЭВМ
и
поступающей
далее
на
исполнительные
.
устройства.'
Они
содержат
цИфроаналоговые
преобразователи
(ЦАП)
и
управляе
мые
буферные
регистры
-
выходные
порты.
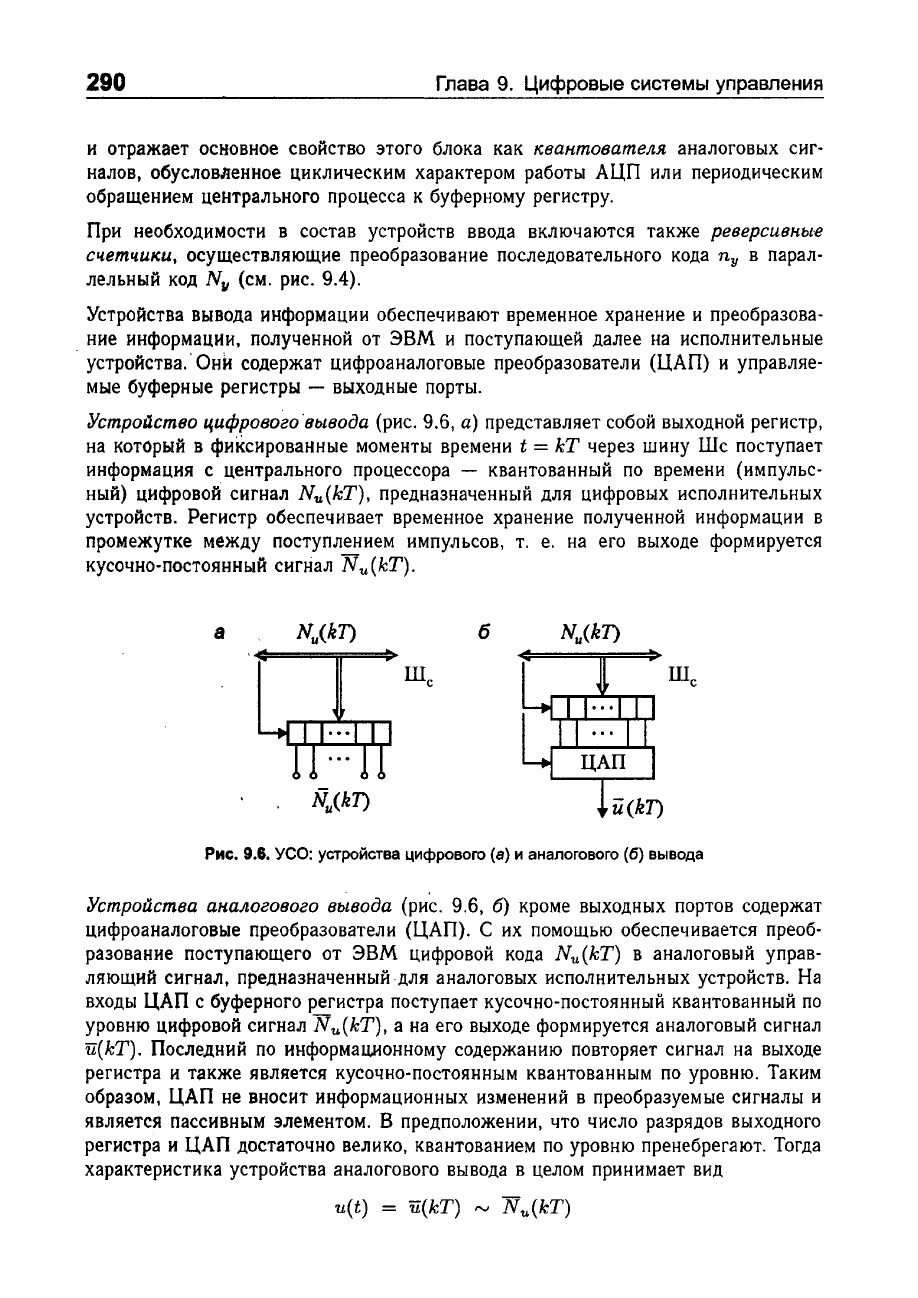
Устройство
цифрового
'вывода
(рис.
9.6,
а)
представляет
собой
выходной
регистр,
на
который
в
фиксированные
моменты
времени
t =
kT
через
шину
Шс
поступает
информация
с
центрального
процессора
-
квантованный
по
времени
(импульс
ный)
цифровоЙ
сигнал
Nu(kT),
предназначенный
для
цифровых
исполнительных
устройств.
Регистр
обеспечивает
временное
хранение
полученной
информации
в
промежутке
между
поступлением
импульсов,
т. е.
на
его
выходе
формируется
кусочно-постоянный
сигнал
N u
(kT).
а
б
Рис.
9.6.
УСО:
устройства
цифрового
(В)
и
аналогового
(6)
вывода
Устройства
аналогового
вывода
(рис.
9.6,
6)
кроме
выходных
портов
содержат
цифроаналоговые
преобразователи
(ЦАП).
С
их
помощью
обеспечивается
преоб
разование
поступающего
от
ЭВМ
цифровой
кода
Nu(kT)
в
аналоговый
управ
ляющий
сигнал,
предназначенный
,для
аналоговых
исполнительных
устройств.
На
входы
ЦАП
с
буферного
регистра
поступает
кусочно-постоянный
квантованный
по
уровню
цифровой
сигнал
N
u(kT),
а
на
его
выходе
формируется
аналоговый
сигнал
u(kT).
Последний
по
информационному
содержанию
повторяет
сигнал
на
выходе
регистра
и
Также
является
кусочно-постоянным
квантованным
по
уровню.
Таким
образом,
ЦАП
не
вносит
информационных
изменений
в
преобразуемые
сигналы
и
является
пассивным
элементом.
В
предположении,
что
число
разрядов
выходного
регистра
и
ЦАП
достаточно
велико,
квантованием
по
уровню
пренебрегают.
Тогда
характеристика
устройства
аналогового
вывода
в
целом
принимает
вид
u(t) =
u(kT)
f'V
N
u(kT)
9.1. " .
.цифровые
системы"
291
и
отражает
основную
особенность
этого
блока
как
фиксатора
дискретных
сиг
налов
(экстраполятора
нулевого
порядка),
обусловленную
своЙ<:;гвом.
выходного
регистра
сохранять
информацию
в
течение
одного
цикла
раБQТЫ.
В
состав
устройства
вывода
часто
включаются
также
широтно-им.nульсные
.мо
дуляторы
(ШИМ,
рис.
9.4),
обеспечивающие
преобразование
цифрового
кода
Nu(kT)
в
широтно-модулированный
сигнал
сигнал
un(t) =
Цn(kТ:)
без
проме
жуточного
преобрззования
к
аналоговой
форме.
9.1.2.
Прохождение
сигналов
и
эквивалентная
схема
цифровой
системы
управления
Для
построения
математической
модели
цифровой
системы
как
системы
дискретно-непрерывного
типа
введем
в
рассмотрение
некоторые
специальные
бло
ки,
отражающие
модельнь}е
особенности
отдельных
элементов
систеlv1ыI~::
рассмот-
peHH~X
в
9.1.1.
. . . '
'.t
а
о
о
б
о
о
в
о
о
't
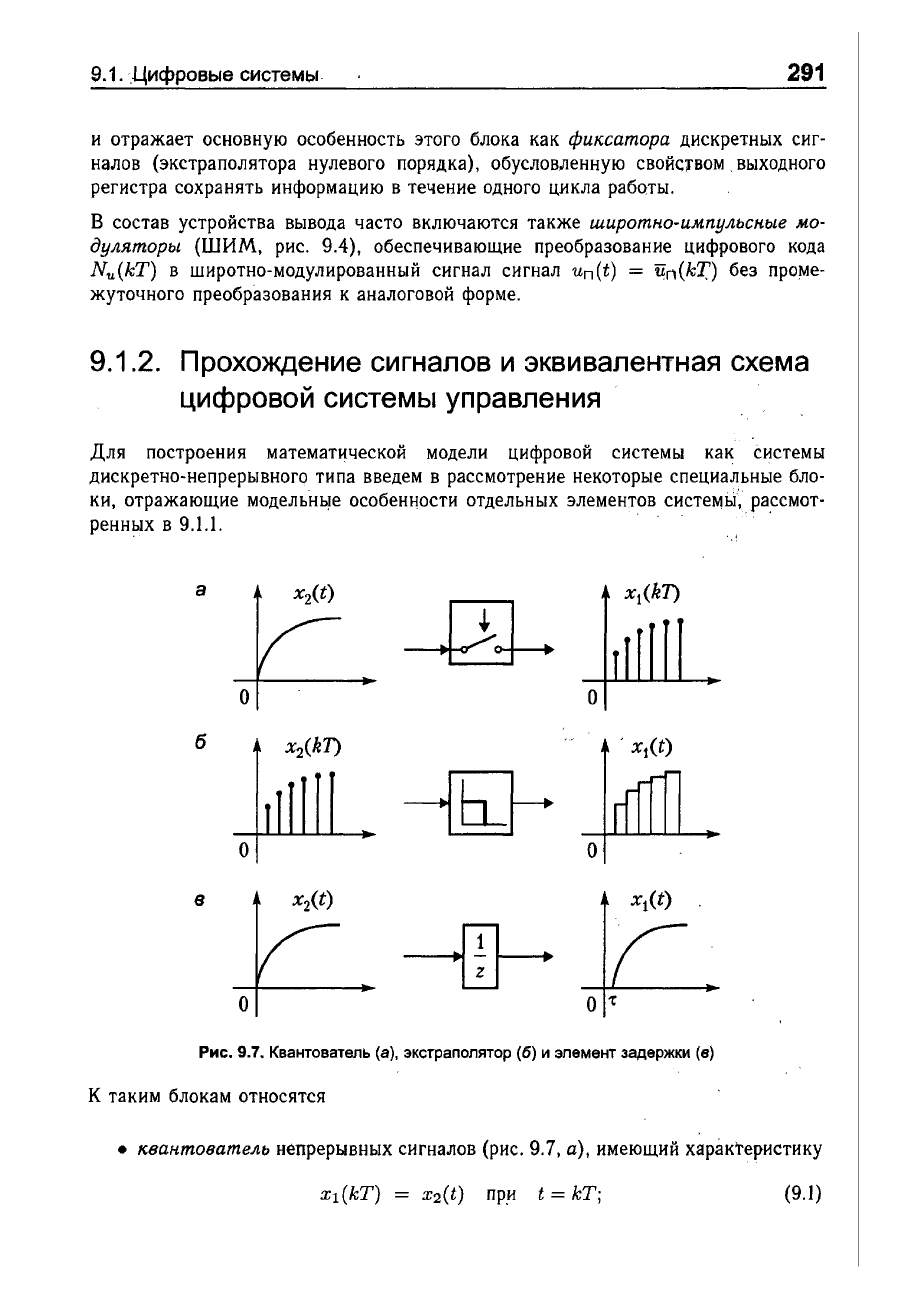
Рис.
9.7.
Квантователь
(8),
экстраполятор
(6)
и
элемент
задержки
(в)
к
таким
блокам
относятся
•
квантователь
непрерывных
сигналов
(рис.
9.7,
а),
имеющий
характеристику
(9.1)

292
Глава
9.
Цифровые
системы
управления
•
фиксатор,
или
экстраполятор
нулевого
порядка
(рис.
9.7,
6),
описываемый
выражением
Xl(t) = X2(kT)
при
t
Е
[kT,
(k +
l)Т);
(9.2)
•
звено
чистого
запаздывания
(элемент
задержки,
см.
8.1.4)
с
характеристи
кой
Xl(t) =
X2(t
-
Т),
где
т
-
время
задержки
(рис.
9.7,
в).
(9.3)
Теперь
рассмотрим
функциональную
схему
цифровой
системы
с
объектом
управ
ления
аналоговой
природы
(рис.
9.8)
и
сигналы
в
различных
ее
точках
(рис.
9.9
и
9.10).
Схема
представлена
самим
ОУ
с
аналоговыми
измерительными
и
исполни
тельными
устройствами,
управляющей
ЭВМ,
таймером
Т,
обеспечивающим
так
тирование
процессов
с
интервалом
Т,
и
устройствами
аналогового
ввода-вывода.
В
предположении
достаточной
разрядности
цифровых
элементов
пренебрежем
эф
фектом
квантования
сигналов
по
уровню
и
отвлечемся
от
различия
между
анало
говыми
и
цифровыми
сигналами,
принимая
во
внимание,
что
в
рамках
указанного
предположения
способ
кодирования
информации
не
влияет
на
информационное
содержание
сигналов.
Отметим,
что
(при
тех
же
предположениях)
работа
цифровых
систем
управле
ния
аналоговыми
процессами
с
цифровыми
измерительными
и
исполнительными
устройствами,
а
также
систем
с
инкриментными
датчиками
и
иными
типами
циф
ровых
устройств
может
быть
рассмотрена
по
той
же
схеме
и
приводит
к
идентичной
математической
модели.
Функциональная
схема
типовой
цифровой
системы
содержит
АЦП,
входным
сиг
налом
которого
является
непрерывный
(неквантованный)
сигнал
y(t)
(точка
А),
а
выходным
кусочно
постоянный
сигнал
y(t) = y(kT)
(точка
В),
который
поступает
на
вход
следующего
блока
-
входного
регистра
ВхР.
Выходом
последнего
слу
жит
шина
управляющей
ЭВМ
(точка
С),
на
которой
в
моменты
ввода
информации
t =
kT
появляется
импульсный
сигнал
y(kT).
Таким
образом,
первые
два
блока
си
стемы
преобразуют
непрерывный
сигнал
y(t)
в
квантованный
по
времени
дискрет
ный
сигнал
y(kT)
(решетчатую
функцию),
т.
е.
представляют
собой
квантователь
y(t)
А
в
с
D
Е
F
Рис.
9.8.
Функциональная
схема
цифровой
системы
9.1.
Цифровые
системы
,293
А
в
с
y(t)
---
y(t)
y(kr)
, 1
о
t
о
т
t
о
т
t
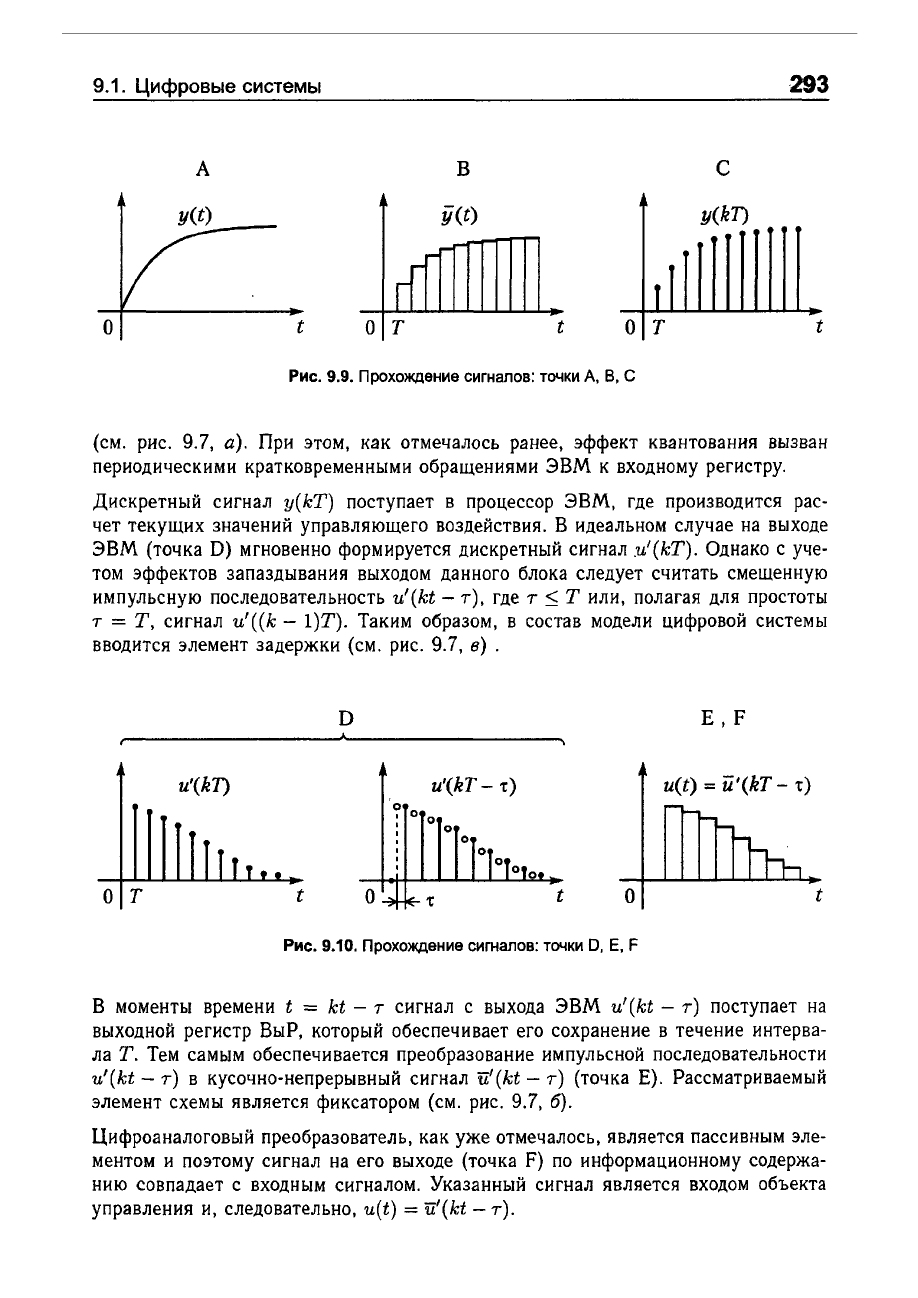
Рис.
9.9.
Прохождение
сигналов:
точки
д,
В,
С
(см.
рис.
9.7,
а).
При
этом,
как
отмечалось
ранее,
эффект
квантования
вызван
периодическими
кратковременными
обращениями
ЭВМ
к
входному
регистру.
Дискретный
сигнал
y(kT)
поступает
в
процессор
ЭВМ,
где
производится
рас
чет
текущих
значений
управляющего
воздействия.
В
идеальном
случае
на
выходе
ЭВМ
(точка
D)
мгновенно
формируется
дискретный
сигнал
.u'(kT).
Однако
с
уче
том
эффектов
запаздывания
выходом
данного
блока
следует
считать
смещенную
импульсную
последовательность
u'(kt -
Т),
где
Т
~
Т
или,
полагая
для
простоты
Т
=
Т,
сигнал
u'((k -
l)Т).
Таким
образом,
в
состав
модели
цифровой
системы
вводится
элемент
задержки
(см.
рис.
9.7,
в)
.
D
E,F
u'(kr) u'(kT - 't)
u(t)
= u'(kT - 't)
'~
о
о
о
т
t t
о
t
Рис.
9.10.
Прохождение
сигналов:
точки
О,
Е,
F
в
моменты
времени
t = kt -
Т
сигнал
с
выхода
ЭВМ
u'(kt -
Т)
поступает
на
выходной
регистр
ВыР,
который
обеспечивает
его
сохранение
в
течение
интерва
ла
Т.
Тем
самым
обеспечивается
преобразование
импульсной
последовательности
u'(kt
-
Т)
в
кусочно-непрерывный
сигнал
u'(kt
-
Т)
(точка
Е).
Рассматриваемый
элемент
схемы
является
фиксатором
(см.
рис.
9.7,
б).
ЦИфроаналоговый
преобразователь,
как
уже
отмечалось,
является
пассивным
эле
ментом
и
поэтому
сигнал
на
его
выходе
(точка
F)
по
информационному
содержа
нию
совпадает
с
входным
сигналом.
Указанный
сигнал
является
входом
объекта
управления
и,
следовательно,
u(t) =
u'(kt
-
Т).

294
Глава
9.
Цифровые
системы
управления
с
учетом
вышеизложенного
может
быть
построена
эквивалентная
схема
цифро
вой
системы
управления,
представленная
на на
рис.
9.11
и
соответствующая
ее
математической
модели
для
случая
линейного
объекта
управления,
линейного
ре
гулятора
и
запаздывания
ЭВМ
т
=
Т.
В
состав
схемы
входит
ОУ
с
передаточной
функцией
Wo(p) ,
цифровой
регулятор
с
передаточной
функцией
K(z),
квантова
тель
К,
элемент
задержки
l/z
и
экстраполятор
Э.
В
более
общем
случае
модель
может
включать
каналы
задающих
воздействий
и
множественные
обратные
связи
по
различным
переменным
системы.
u'«k-1)1)
1----...
tl
э
u(t)
Рис.
9.11.
Эквивалентная
схема
цифровой
системы
9.1.3.
Особенности
цифровых
систем
ОУ
Основной
особенностью
функционирования
цифровой
системы
является
цифро
вой
способ
обработки
информации
в
регуляторе
(управляющей
ЭВМ).
Такой
спо
соб
предусматривает
использование
только
арифметических
операций
и
позволяет
легко
реализовывать
алгебраические
алгоритмы
управления
и
сводящиеся
к
ним
рекуррентные
процедуры.
Так
как
последние
представляют
собой
решения
раз
ностных
уравнений,
то
Можно
сказать,
что
цифровая
обработка
информации
и
ориентирована
на
решение
уравнений
такого
типа.
При
этом
возможность
непо
средственной
ре~лизации
динамических
алгоритмов
управления
(см.
главу
7),
за
писанных
в
виде
дифференциальных
либо
интегральных
уравнений,
исключается,
и
поэтому
подобные
алгоритмы
также
должны
быть
приведень~
к
рекуррентной
форме.
Прuмер
9.1.
Простейший
пропорциональный
алгоритм
управления
имеет
вид:
u
К
6,
6 =
у*
-
у.
(9.4)
(9.5)
Выражения
содержат
Только
операции
сложения
и
умножения
и
поэтому
легко
реализуются
на
управляющей
ЭВМ
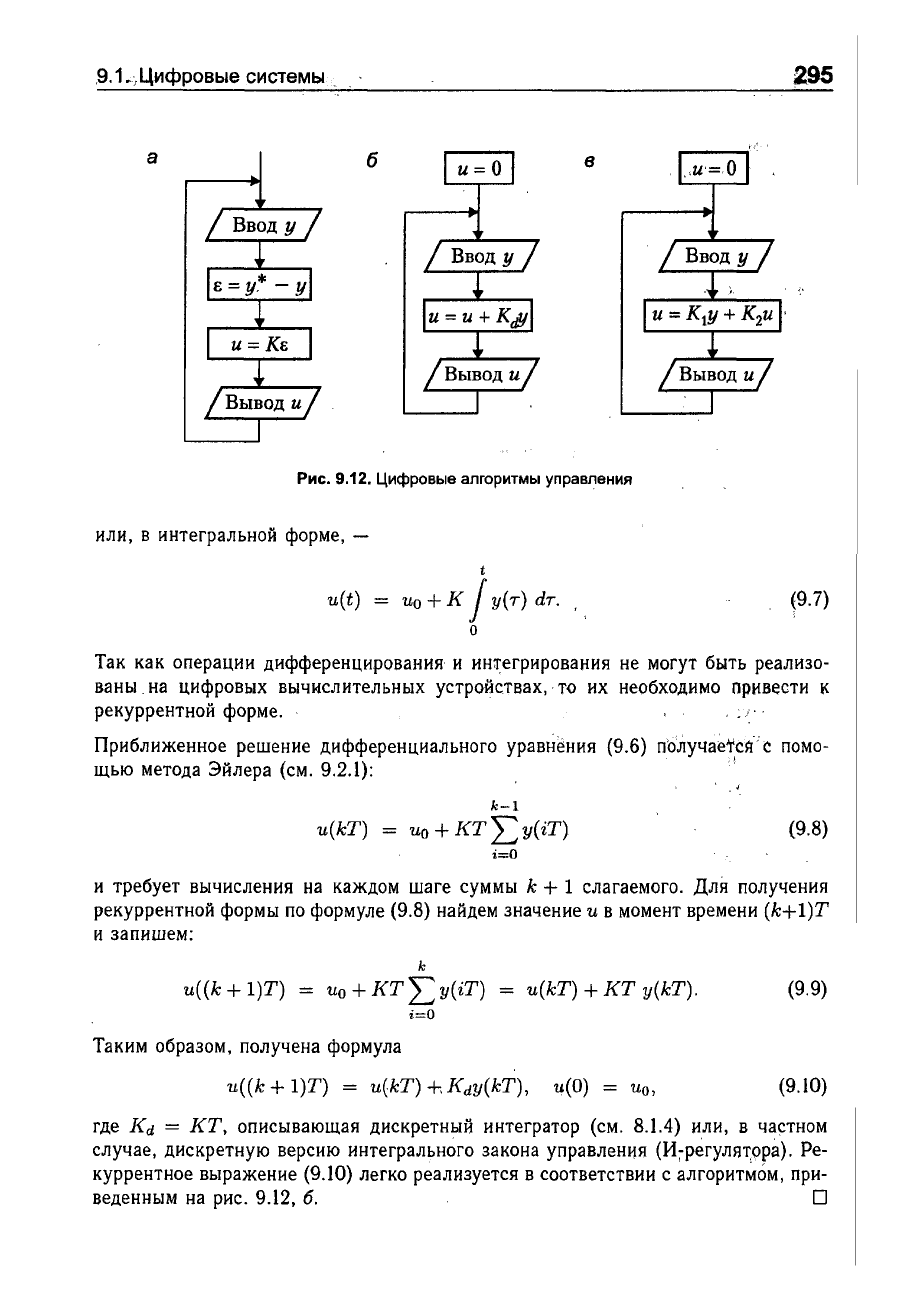
(рис.
9.12,
а).
О
Прu.м.ер
9.2.
Наиболее
распространенным
элементом
динамических
регуляторов
я~ляется
интегрируюI1J.ее
звено,
описываемое
ДИфференциальным
уравнением
u(t) =
к
y(t),
и(О)
=
ио,
(9.6)
,9.1
..
j
Цифровые
системы.
"
295
а
б
в
Рис.
9.12.
Цифровые
алгоритмы
управления
или,
в
интегральной
форме,
-
t
u(t) =
ио
+
К
!
У(Т)
dT.
(9.7)
О
Так
как
операции
дифференцирования,
и
ИН:J;егрирования
не
могут
быть
реализо
ваны.
на
цифровых
вычислительных
устройствах,·
то
их
необходимо
привести
к
рекуррентной
форме.
...
,
Приближенное
решение
дифференциального
урав»ения
(9.6)
п\О'луча~tсsi:с
помо-
щью
метода
Эйлера
(см.
9.2.1):
,.!
, . "
k-l
u(kT)
=
uo+KTLy(iT)
(9.8)
i=O
и
требует
вычисления
на
каждом
шаге
суммы
k + 1
слагаемого.
Для
получения
рекуррентной
формы
по
формуле
(9.8)
найдем
значение
u
в
момент
времени
(k+l)T
и
запишем:
k
u«k+l)T)
=
uo+KTLy(iT)
=
u(kT)+KTy(kT).
(9.9)
i=O
Таким
образом,
получена
формула
u«k
+
l)Т)
=
u(kT)
+.
Kdy(kT),
и(О)
=
ио,
(9.10)
где
Kd =
КТ,
описывающая
дискретный
интегратор
(см.
8.1.4)
или,
в
ча~тном
случае,
дискретную
версию
интегрального
закона
управлеЮiЯ
(и~регуляr~ра).
Ре
куррентное
выражение
(9.10)
легко
реализуется
в
соответствии
с
алгоритмом,
при
веденным
на
рис.
9.12,
б.
О

296
Глава
9.
Цифровые
системы
управления
Замечание
9.1.
Вывод
основной
формулы
(9.8)
предусматривает
замену
непре
рывной
функции
y(t)
кусочно-постоянной
функцией
y(kT)
.
Такая
замена
(ап
проксимация
нулевого
порядка)
и
вызывает
методическую
ошибку
расчетов
по
рекурентной
формуле
(9.10).
Для
повышение
точности
требуется
уменьшение
ин-
fi(k1)
тервала
дискретности
Т,
что
связано
с
ускорением
вы
числений.
Использование
более
точных
приема
в
ап
проксимации
функции
y(t),
характерное
для
более
со
вершенных
методов
цифрового
интегрирования
(на
пример,
методов
Рунге-Кутта,
Адамса
и
др.)
и,
сле-
О
т
kT t
довательно,
более
сложных
вычислительных
процедур
позволяет
также
уменьшить
методическую
ошибку
ин
тегрирования.
Во
всех
случаях
умешьшение
ошибки
связано
с
необходимостью
ускорения
вычислений
и
использованием
более
быстро
действующих
ЭВМ.
Замечание
9.2.
При
условии,
что
сигнал
у
является
кусочно
постоянным:
у
=
=
fj(kT),
рассмотренный
метод
цифрового
интегрирования
позволяет
получить
аб
солютно
точные
значения
переменной
u(t)
в
дискретные
моменты
времени
t =
kT
и
не
приводит
к
получению
методической
ошибки.
Такая
ситуация,
нехарактерная
для
цифровых
регуляторов.
где
сигнал
у
имеет
непрерывную
природу,
наблюдает
ся
в
объектах
управления
цифровых
систем,
на
вход
которых
поступает
кусочно
постоянный
сигнал
управления
u(t).
Данное
свойство
используется
при
дискрети
зации
непрерывных
объектов
и
приводит
к
получению
точных
дискретных
моделей
линейных
ОУ
(см.
9.2.1).
Таким
образом,
цифровой
способ
обработки
информации
в
цифровых
САУ
вызы
вает
необходимость
использования
дискретных
моделей
регуляторов.
Принимая
во
внимание
непрерывную
(неквантованную)
природу
большинства
реальных
управ
ляемых
процессов,
приходим
к
следующему
выводу.
Основная
модельная
особенность
цифровой
системы
заключается
в
том,
что
она
является
дискретно-непрерывной
и
описывается
как
разностными,
так
и
дифференциальными
уравнениями.
Для
линейного
случая
-
это
уравнения
регулятора,
например,
дискретная
опера
торная
модель
u'(kT)
=
K(z)y(kT),
(9.11)
и
непрерывные
операторные
уравнения
ОУ
типа
y(t) = Wo(p)y(t),
{9.l2)
где
K(z)
и
Wo(p)
-
соответствующие
передаточные
функции.

9.1.
Цифровые
системы
297
Сопряжение
двух
указанных
частей
модели
осуществляется
с
помощью
квантова
теля
и
экстраполятора
нулевого
порядка.
Кроме
отмеченных
выше
особенностей
функционирования
цифровой
системы,
свя
занных
с
цифровым
способом
обработки
информации,
последний
вызывает
также
временную
задержку,
обусловленную
потерями
времени
на
выполнение
вычисле
ний
на
каждом
цикле
работы
ЭВМ
(см.
8.1.1-8.1.2).
Это
явление
отражается
в
модели
системы
в
виде
звена
чистого
запаздывания,
связывающего
идеальный
сигнал
на
выходе
дискретного
регулятора
u'(kT)
с
реальным
смещенным
сигна
лом
u(kT)
=
u'(kT
-
Т),
поступающий
после
экстраполяции
на
вход
ОУ.
Полагая
Т
=
Т,
запишем
1
u(kT)
=
-u'(kТ).'
z
(9.13)
При
исследовании
цифровой
системы
последнее
уравнение
может
рассматриваться
как
описание
дополнительного
элемента
регулятора
или
быть
отнесено
к
модели
ОУ
(см.
при
мер
9.3
и
9.2.2).
Указанные
выше
особенности
моделей
цифровых
систем
и
в
первую
очередь
их
дискретно-непрерывная
природа
обусловливают
основные
трудности
анализа
и
проектирования.
В
связи
с
этим
нашли
распространение
два
подхода
к иссле
дованию
цифровых
систем:
•
с
использование
теории
непрерывных
систем;
•
с
использование
теории
дискретных
систем.
Первый
подход
предусматривает
построение
непрерывного
регулятора,
например
u(t)
= K(p)y(t),
(9.14)
и
его
последующую
дискретизацию,
т.
е.
приведение
к
дискретной
форме
(9.11).
Основной
недостаток
такого
подхода
заключается
в
наличии
методической
ошибки
(см.
замечание
9.1).
Кроме
того,
подход
не
позволяет
учесть
эффекта
запаздыва
ния
цифрового
регулятора.
Несмотря
на
это
подход
получил
достаточно
широ
кое
распространение
ввиду
его
простоты
и
возможности
достижения
приемлемо
го
качества
процессов
при
использовании
быстродействующих
вычислительных
устройств,
обеспечивающих
возможность
получения
малого
значения
интервала
квантования
Т.
Второй
подход
предполагает
дискретизацию
самого
объекта
управления,
т.
е.
его
приведение
к
виду
y(kT)
= Wd(z)u(kT),
(9.15)
а
затем
синтез
дискретного
регулятора.
Подход
лишен
основной
методической
ошибки
(см.
замечание
9.2)
и
позволяет,
кроме
того,
принять
во
внимание
запаз
дывание
ЭВМ
путем
соответствующего
расширения
дискретной
модели
объекта
(см.
при
мер
9.3
и
9.2.1).

Глава
9.
Цифровые
системы
управnения
ПРU'м'ер
9.3.
Рассмотрим
простейший
объект
управления,
представленный
инте-
грируюiI:iнм"зве~
.!
iJ(t)
=
Ко
u(t),
у(О)
=
уо,
(9.16).
или,
в
операторнрЙ
форме,
-
y(t)
Ко'
=
-u(t),
Р
(9.17)
где
входной
сигнал
u(t)
является
выходом
буферного
регистра
и
поэтому
являет
ся
кусочно-постоянным.
В
силу
последнего
получаем
точную
дискретную
модель
объекта
(см.
пример
9.2
и
замечание
9.2)
y«k
+
l)Т)
= y(kT) +
Ь
u(kT),
где
Ь
=
КоТ
или
в
операторной
форме
-
ь
y(kT) =
-u(kТ).
z-l
(9.18)
(9.19)
Принимая
во
внимание,
что
входной
сигнал
u(kT)
является
запаздывающим
по
сравнению
с
идеальным
сигналом
на
выходе
цифрового
регулятора
u'(kT)
(см.
9.1.2),
т.
е.
u«k
+
l)Т)
= u'(kT),
(9.20)
введем
в
рассмотрение
дополнительный
динамический
элемент
-
звено
чистого
запаздывания,
и
запишем
u(kT) = ! u'(kT).
- z
(9.21)
Таким
образом,
расширенная
модель
ОУ
с
учетом
запаздывания
описывается
раз
ност~ыми
уравнениями
(9.18), (9.20)
или
в
операторном
виде
-
y(kT)
=
z(z
~
1)
u'(kT).
(9.22)
Задачи
управления
дискретным
объектом
(9.18), (9.20)
решаются
стандартными
методами
теории
дискретных
динамических
систем.
Так,
для
решения
задачи
ста
билизации
H)1.l1eBOfO
значения
выходной
переменной
у
(или
переменных
состояния
(у,
и)
расширенного
ОУ)
используется
модальный
регулятор
алгоритм
работы
которого
представлен
на
рис.
9.12,
в.
(9.23)
О

9.2.
Проблемы
дискретизации
непрерывных
моделей
299
9.2.
Проблемы
дискретизации
непрерывных
моделей
B~
пр6цессе
исследования
цифровых
систем возникает
задача
преобразования
непрерывных
динамических
моделей
регуляторов
или
объектов
управления
к
дис
кретной
форме
с
учетом
особенностей
цифровой
обработки'
ИНформации,
рассмот
ренных
в
п.
9.1.
При
этом
кроме самой
процедуры
дискретизации
большой
интерес
представляют
также
вопросы
учета
запаздывания
ЭВМ
и
выбора
интервала
кван
тования.
9.2.1.
Методы
дискретизации
t-T
t
t+T
Метод
Эйлера.
Метод
предлагает
приближенное
и
наи
более
простое
решение
задачи
дискретизации
моделей
динамических
систем.
Он
основан
нз,
формулах
прибли
женного
вычисления
производной
непрерывной
функ
ции
(или
приближенного
вычисления
определенного
ИН
теграла).
Рассмотрим
функцию
x(t)
в
малой
окрестно
сти
произвольной
точки
t,
а
также
ее
значения
x(t
+
Т)
и
x(t
-
Т)
в
точках
t +
Т
и
t -
Т
соответственно.
Для
расчета
производной
±(t) = dx(t)/dt
в
точке
t
можно
воспользоваться
одним
из
двух
выражений:
dx
дх+
x(t
+
Т)
- x(t)
(9.24)
~
=
dt
At
Т
dx
дх-
x(t) -
x(t
-
Т)
(9.25)
~
dt
At
Т
При
этом
приращения
функции
на
интервале
Т,
т.
е.
дх+
и
Ах-
называют
ся,
соответственно,
nрям,ой
и
обратной
(возвратной)
разностям,и.
Выражения
(9.24)-(9.25)
дают
точные
описания
производных
при'
Т
--+
О,
а
при
любых
конеч
НЫХ
значениях
интервала
Т,
вообще
говоря,
приводят
к
появлению
методических
ошибок.
Метод
Эйлера
позволяет
произвести
замену
производных
в
дифференциальных
ypaBJ-Jениях,
описывающих
непрерывные
динамические
процессы,
на
приближен
ные
рекуррентные
выражения,
и
в
результате
получить
дискретные
описа,Ния
про
цессов.
Найдем
дискретную
модель
линейной
системы
(объекта
управления)
±(t) = Ax(t) + Bu(t),
y(t) = Cx(t),
(9.26)
(9.27)
