Морозов А.В. Домашняя работа по алгебре за 7 класс
Подождите немного. Документ загружается.

161
44. Решение задач с помощью систем уравнений
№1165.
Если x — I число, y — II число, то
{
63
12
xy
xy
+
=
−
=
,
{
275
251
x
y
=
=
,
{
37 5
25 5
x
,
y,
=
=
I число = 37,5; II число = 25,5.
Ответ: 37,5; 25,5.
№1166.
Если в феврале выпустили x изделий, то (x – 165) = y изделий выпустили в
январе. По условию за два месяца выпустили 1315 изделий.
{
165
1315
xy
xy
−=
+=
,
{
2 1480
2 1150
x
y
=
=
,
{
740
575
x
y
=
=
Ответ: в январе выпустили 575 изделий, в феврале — 740 изделий.
№1167.
Если x бригад работают на бригадном подряде, а y — число обычных бри-
гад, то
{
5
31
xy
xy
−=
+=
,
{
236
226
x
y
=
=
,
{
18
13
x
y
=
=
Ответ: на бригадном подряде работают 18 бригад.
№1168.
Если легковых машин x, а грузовых y, то
{
8
22
yx
yx
−=
+=
,
{
230
214
y
x
=
=
,
{
15
7
y
x
=
=
Ответ: отремонтировали 15 грузовых машин.
№1169.
Если тракторов x, а автомашин y, то
{
28
18
xy
x
,y
+=
=
,
{
18 28
18
,y y
x,y
+=
=
,
{
28 28
18
,y
x
,y
=
=
,
{
10
18
y
x
=
=
Ответ: 18 тракторов, 10 автомашин.
№1170.
Если боковая сторона x см, а основание y см, то
{
7
243
yx
yx
−=
+=
,
{
336
7
x
yx
=
=+
,
{
12
19
x
y
=
=
Ответ: 12 см — боковая сторона, 19 см — основание.
№1171.
Если плотность Al x кг/дм
3
, а плотность Fe y кг/дм
3
, то
{
51
0 6 1 5 13 32
yx ,
,x ,y ,
−=
+=
,
{
06 06 306
1 5 0 6 13 32
,y ,x ,
,y ,x ,
−=
+=
,
{
2 1 16 38
51
,y ,
yx ,
=
−=
,
{
78
27
y,
x
,
=
=
Ответ: 2,7 кг/дм
3
— плотность алюминия, 7,8 кг/дм
3
— плотность железа.
№1172.
Если сначала собирали x кг картофеля с 1 га, а новая урожайность картофе-
ля с 1 га составила y кг, то
{
4000
320 400 640000
yx
yx
−=
−=
,
{
4 4 16000
4 5 8000
yx
yx
−=
−=
,
{
4000
16000 8000
yx
x
=+
=−
,
{
8000
12000
x
y
=
=
Ответ: 8т — первоначальная урожайность, 12т — новая урожайность кар-
тофеля.

162
№1173.
Если скорость поезда x км/ч, скорость машины y км/ч, то
{
5
4 7 640
xy
yx
−=
+=
,
{
5
4 7(5 ) 640
xy
yy
=+
++=
,
{
5
11 605
x
y
y
=
+
=
,
{
60
55
x
y
=
=
Ответ: 55 км/ч — скорость автомашины, 60 км/ч скорость поезда.
№1174.
Если x — I число, а y — II число, то по условию
{
34 47
21
xy
yx
+=
−=
,
{
34 47
36 3
xy
xy
+=
−+ =
,
{
10 50
21
y
x
y
=
=
−
,
{
5
9
y
x
=
=
Ответ: 9 — I число, 5 — II число.
№1175.
Если x км/ч — скорость теплохода по течению, y км/ч — скорость теплохо-
да против течения, то
{
3 2 240
3235
xy
yx
+=
−=
,
{
6 4 480
6 9 105
xy
xy
+=
−+ =
,
{
13 585
3235
y
yx
=
−
=
,
{
45
135 2 35
y
x
=
−=
,
{
45
2 100
y
x
=
=
,
{
45
50
y
x
=
=
Ответ: 50 км/ч — скорость теплохода по течению, 45 км/ч — скорость теп-
лохода против течения.
№1176.
Если скорость I автомобиля x км/ч, второго — y км/ч, то по условию
{
2 2 280
14 14 280
xy
xy
+=
−=
,
{
140
20
xy
xy
+=
−=
,
{
2 160
2 120
x
y
=
=
,
{
80
60
x
y
=
=
Ответ: 80 км/ч — скорость I автомобиля, 60 км/ч — скорость II автомобиля.
№1177.
Если скорость I туриста x км/ч, а второго y км/ч, то
{
4438
44 2
xy
xy
+=
−=
,
{
840
836
x
y
=
=
,
{
5
45
x
y,
=
=
Ответ: 5 км/ч — скорость I туриста, 4,5 км/ч — скорость II туриста.
№1178.
Если собственная скорость лодки x км/ч, а y км/ч — скорость реки, то
{
4( ) 5( )
35( ) 70
x
yxy
,x y
+= −
+=
,
{
445 0
7 7 140
xyxy
xy
+−+=
+=
,
{
90
20
yx
yx
−
=
+=
,
{
10 20
9
y
x
y
=
=
,
{
2
18
y
x
=
=
Ответ: 18км/ч — собственная скорость лодки, 2км/ч — скорость течения реки.
№1179.
Если собственная скорость лодки x км/ч, а y км/ч — скорость течения реки,
то по условию получим
3( ) 4( ) 380
1
()()85
2
xy xy
xy xy
++ −=
⎧
⎪
⎨
++ −=
⎪
⎩
,
{
3344 380
2 2 170
xyxy
xyxy
++−=
++−=
,
{
7 380
3 170
xy
xy
−=
+=
,
{
10 20
9
y
x
y
=
=
,
{
55
5
x
y
=
=
Ответ: 55 км/ч — скорость лодки, 5 км/ч — скорость течения.
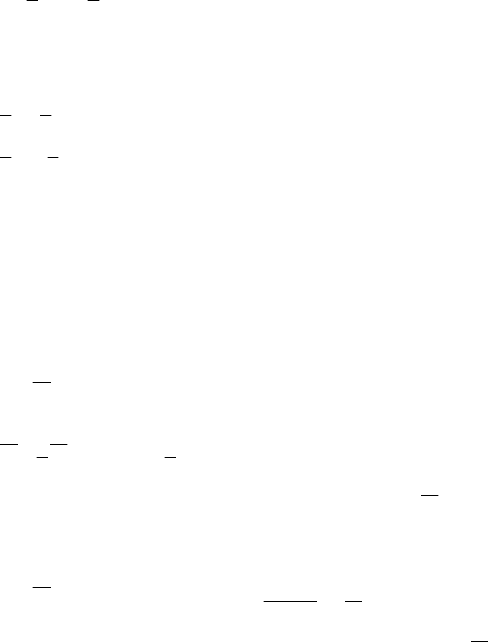
163
№1180.
Если на I полке x книг, а на второй y, то
55
11
4
22
xy
x
yy
+=
⎧
⎪
⎨
+=⋅
⎪
⎩
,
{
55
15 0
xy
x,y
+=
−=
,
{
25 55
15
,y
x
,y
=
=
,
{
22
33
y
x
=
=
Ответ: 33 книги — на I полке, 22 книги — на II полке.
№1181.
Если x — I число, y — II число, то
12
2
23
11
159
66
xy
xy
⎧
−=
⎪
⎨
⎪
+=
⎩
,
{
3412
7 354
xy
xy
−=
+=
,
{
3412
3 21 1062
xy
xy
−=
−− =−
,
{
25 1050
354 7
y
x
y
−=−
=−
,
{
42
60
y
x
=
=
Ответ: 42 — II число, 60 — I число.
№1182.
Если плотность железа x г/см
3
, а меди y г/см
3
, то
{
4 5 8 101 5
32 68
,x y ,
xy,
+=
−=
,
{
4 5 8 101 5
12 8 27 2
,x y ,
x
y,
+=
−=
,
{
16 5 128 7
2368
,x ,
yx,
=
=−
,
{
78
83
x
,
y,
=
=
Ответ: 7,8 г/ см
3
— плотность железа, 8,3 г/см
3
— плотность меди.
№1183.
Если xy — задуманное число, то
9
2
9
xy
yx xy
+=
⎧
⎪
⎨
=
⎪
⎩
,
9
2
10 (10 )
9
xy
yx xy
=−
⎧
⎪
⎨
+= +
⎪
⎩
,
{
9
90 9 20 2
xy
yx xy
=−
+= +
,
{
9
88 11 0
xy
yx
=−
−=
,
{
9
88 11 9 0
xy
y(y)
=−
−−=
,
{
9
99 99
x
y
y
=
−
=
,
{
8
1
x
y
=
=
,
x
y = 81
Ответ: 81 — задуманное число.
№1184.
Если xy — задуманное число, то
10
(1)2
xy
yx xy
+=
⎧
⎨
+=
⎩
,
{
10
10 1 20 2
xy
yx x y
=−
++= +
,
{
10
8 19(10 ) 1
xy
yy
=−
−
−=−
,
{
10
27 189
x
y
y
=
−
=
,
{
3
7
x
y
=
=
,
x
y = 37
Ответ: 37 — задуманное число.
№1185.
Если озимыми занято x га, а яровыми y га, то
{
480
0 2 300 0 75
xy
,x , y
−=
+=
,
{
480
0 2 0 75 300
xy
,x , y
=+
−=−
,
{
480
0 2( 480) 0 75 300
xy
,y , y
=+
+− =−
,
{
480
0 55 396
xy
,y
=+
−=−
,
{
1200
720
x
y
=
=
Ответ: 1200 га занято озимыми, 720 га занято яровыми.
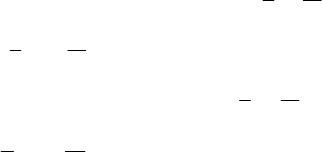
164
№1186.
Если I бригада изготовила x деталей, а вторая y деталей, то по условию
{
680
0 2 0 15 118
xy
,x , y
+=
+=
,
{
0 2 0 2 136
0 2 0 15 118
,x ,y
,x , y
−− =−
+=
,
{
005 18
680
,y
x
y
−
=−
=−
,
{
360
320
y
x
=
=
Ответ: 320 деталей изготовила I бригада, 360 деталей изготовила II бригада.
№1187.
а) (a–2)(a
2
+ a – 1) – a
2
(a – 1) = a
3
+ a
2
– 2
2
– 2a + 2 – a
3
+ a
2
= –3a+2;
б) (3 – p)(9 + 3p + p
2
) – (1 – p
3
) = 27 – p
3
– 1 + p
3
= 26.
№1188.
а) 0,064m
3
+ 1 = (0,4m + 1 )(0,16m
2
– 0,4m + 1);
б) 0,027x
3
– y
3
= (0,3x – y)(0,09x
2
+ 0,3xy + y
2
);
в) p
6
+ 8 = (p
2
+ 2)(p
4
– 2p
2
+ 4); г) 27 – m
6
= (3 – m)(9 + 3m
2
+ m
4
).
№1189.
(x
3
– y
3
)
2
+ 2x
3
y
3
= (x
2
+ y
2
)(x
4
+ y
4
– x
2
y
2
);
(x
3
– y
3
)
2
+ 2x
3
y
3
= x
6
– 2x
3
y
3
+ y
6
+ 2x
3
y
3
= x
6
+ y
6
;
(x
2
+ y
2
)(x
4
+ y
4
– x
2
y
2
) = x
6
+ y
6
.
№1190.
а) 2x + 5y = 12, 5y = –2x + 12, y = –
212
55
x
+
,
–
2
5
< 0;
12
5
> 0 — проходит в I, II и IV координатных четвертях.
б) 3x – 4y = 10, 4y = 3x – 10, y =
3
4
x –
10
4
,
4
3
> 0; –
4
10
< 0 — проходит в I, III и IV координатных четвертях.
№1191.
y = –x
2
– 6x – 11,
–x
2
– 6x – 11 = –(x
2
+ 6x + 9) – 2 = –(x + 3)
2
– 2 < 0, значит, y < 0 для любого
x. Тогда график лежит в нижней полуплоскости.
Дополнительные упражнения к главе VI
К параграфу 15
№1192.
x
2
– 2y = 7;
а) При x = 5, y = 8, 25 – 16 = 7; 9 ≠ 7 ⇒ не решение;
б) При x = –4, y = –11,5, + 23 = 7; 39 ≠ 7 ⇒ не решение;
в) При x = –1, y = –3, 1 + 6 = 7; 7 = 7 ⇒ решение;
г) При x = 1,2, y = –2,78, 1,44 + 2 ⋅ 2,78 = 7;
1,44 + 5,56 = 7; 7 = 7 ⇒ решение.
№1193.
а) u – 3v = 1; б) u – v = 7;
в) 4 + v = – 0,2; г) 2u – v = 0,8.

165
№1194.
ax + by = 81. Пусть a, b — целые числа.
15a оканчивается на 5 или 0, 40b оканчивается на 0 ⇒ (15; 40) — не реше-
ние.
№1195.
а) a ⋅ 5 – 2 ⋅ 7 = 1, 5a – 14 = 1, 5a = 15, a = 3;
б) 5 ⋅ (–3) + 8 ⋅ b = 17, –15 + 8b = 17, 8b =32, b = 4.
№1196.
а) x + y = 11,
(1;10); (10;1); (2; 9); (9; 2); (3; 8); (8; 3); (4; 7); (7; 4);(5; 6); (6; 5) — решения.
б) xy = 18, (1; 18); (18; 1); (2; 9); (9; 2); (3; 6); (6; 3) — решения.
№1197.
(a = 19; b = 23); (a = 13; b = 29); (a = 11; b = 31); (a = 5; b = 37);
(a = 22; b = 19); (a = 29; b = 13); (a = 31; b = 11); (a = 37; b = 5).
№1198.
Если двухрублевых x, а пятирублевых y, то 2x + 5y = 23. Целочисленные
решения системы, при которых x > 0, это: (9; 1) и (4; 3).
Ответ: 9 монет или 4 монеты.
№1199.
Если задуманное число xy , то xyxy ⋅= 2111 , т.е.
1000 + 100x + 10y – 210x – 21y = –1001, –100x – 11y = –1001,
10x + y = 91, x = 9, y = 1. Значит, задумано 91.
Ответ: 91.
№1200.
y – x
2
= 9.
а) Пусть график пересекается с Оx в точке с ординатой, равной 0, т.е.
y = 0, –x
2
= 9 — такого быть не может, значит, график не пересекается с Оx.
б) График функции пересекает ось Оy в точке с абсциссой, равной 0, т.е. x =
0 ⇒ y = 9, значит, A(0; 9) — точка пересечения с Оy.
№1201.
x
3
– y – 2 = 0
а) M(–1; –3) (–1)
3
– (–3) – 2 = –1 + 3 – 2 = 0 M ∈ графику;
б) K(–1; 1) (–1)
3
– 1 – 2 = –2 – 2 = –4 ≠ 0 K ∉ графику;
в) B(1; –1) 1
3
– (–1) – 2 = 2 – 2 = 0 B ∈ графику.
№1202.
x – xy = 46; A(x; –1,3), т.к. A ∈ графику, то x – x(–1,3) = 46, 2,3x = 46, x = 20.
Ответ: (20; –1,3).
№1203.
8x – 5y = 14; B(1,2; y), B ∈ графику, значит
8 ⋅ 1,2 – 5y = 14, 9,6 – 5y = 14, 5y = –4,4, y = –0,88, т.е. B(1,2; 0,88).
№1204.
3x + 2y = 4, y = –1,5x – 2.
График функции проходит в II, III и IV координатных четвертях. Т.к. если у
точки обе координаты положительны, то она лежит в I четверти и не при-
надлежит графику.
166
№1205.
6x – 12y = 5, y =
15
26
x
⎛⎞
−
⎜⎟
⎝⎠
. Чтобы y была целой, надо, чтобы по крайней ме-
ре x –
5
6
было целым, но x также целое, значит, такой точки быть не может.
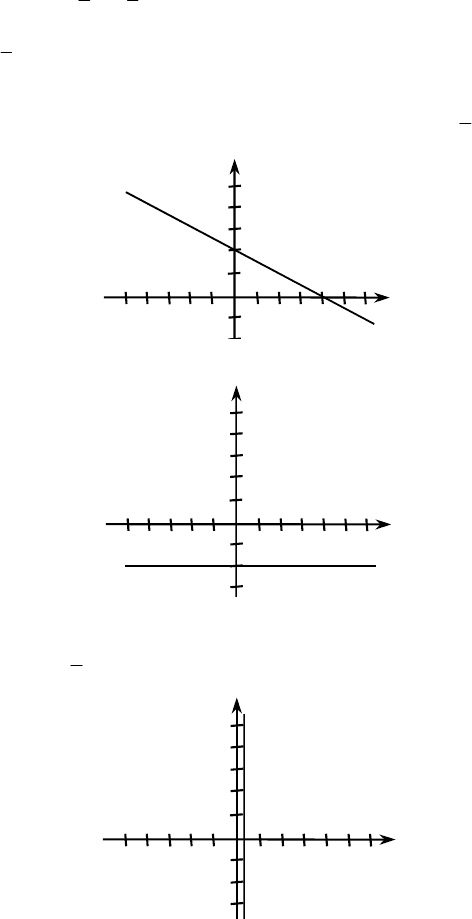
№1206.
а) 3(x– 2y) – 2(x – 4y) = 4, 3x – 6y – 2x + 8x = 4, x + 2y=4, y=2–
2
x
;
1
5
3
y
x
35
–
5
–
3
–
1
L
0
–
1
1
б) 2(0,5x–1,2y) – (0,6y + x) = 6, x – 2,4y – 0,6y – x = 6, –3y = 6, y=–2;
1
5
3
y
x
35
–
3
–
5
–
3
–
1
L
0
–
1
1
в) 3(0,4y – 0,2x) – 4(0,3y – 0,6x) = 0,6, 1,2y – 0,6x – 1,2y + 2,4x = 0,6,
1,8x = 0,6, x =
3
1
1
5
3
y
x
35
–
3
–
5
–
3
–
1
L
0
–
1
1
167
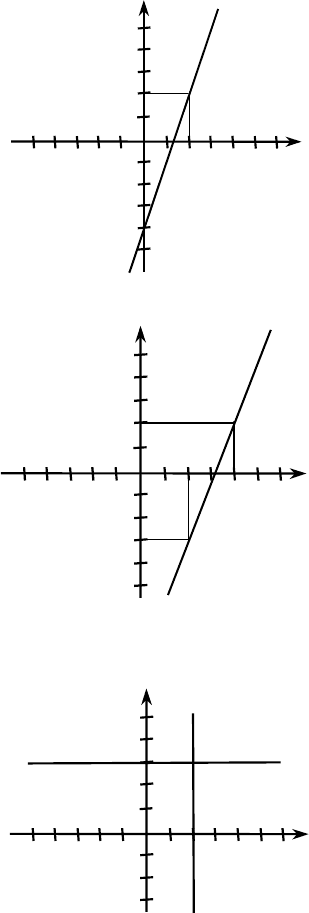
№1207.
ax –y = 4; M(3; 5), a ⋅ 3 – 5 = 4, a = 3, 3x – y = 4, y = 3x – 4.
1
5
3
y
x
35
–
5
–
3
–
5
–
3
–
1
L
0
–
1
1
№1208.
y – 2,5x = c; K(2; –3); –3 – 2,5 ⋅ 2 = c, c = –8, y = –2,5 – 8.
1
5
3
y
x
35
–
5
–
3
–
5
–
3
–
1
L
0
–
1
1
№1209.
а) (x – 2)(y – 3) = 0,
при x = 2: y — любое,
при y = 3: x — любое;
1
5
3
y
x
35
–
3
–
5
–
3
–
1
L
0
–
1
1
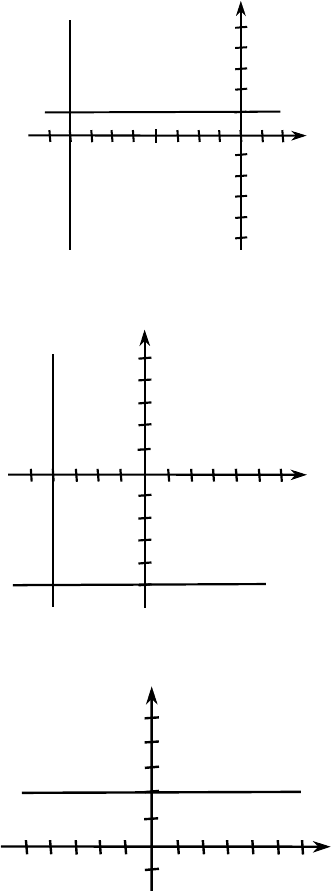
168
б) (x + 8)(y – 1) = 0,
при x = –8: y — любое, при y = 1: x — любое;
x
–
7
–
9
–
1
1
5
3
y
–
5
–
3
–
5
–
3
–
1
0
1
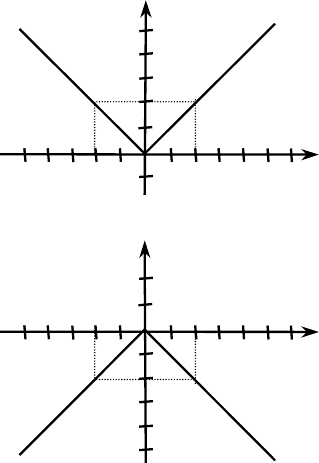
в) (x + 4)(y + 5) = 0
при x = –4: y — любое; при y = –5: x — любое
1
5
3
y
x
35
–
5
–
3
–
5
–
3
–
1
L
0
–
1
1
г) x(y – 3) = 0,
при x = 0: y — любое, при y = 2: x — любое.
1
5
3
y
x
35
–
5
–
3
–
1
L
0
–
1
1
169
№1210.
(x + 2)(y + 3) = 0,
при x = –2: y — любое, (–2; 0) — точка пересечения с осью Оx
при y = –3: x — любое, (0; –3) — точка пересечения с осью Оy
№1211.
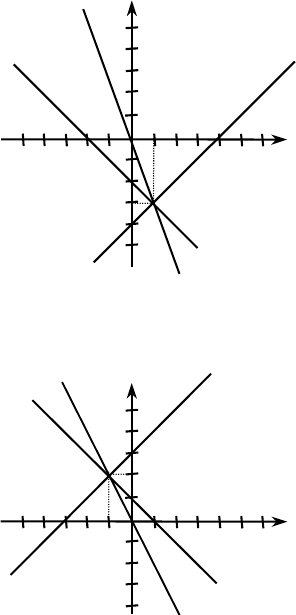
а) y = |x|
1
5
3
y
x
35
–
5
–
3
–
1
0
–
1
1
б) y = –|x|.
0
1
y
x
35
–
5
–
3
–
5
–
3
–
1
–
1
1
№1212.
22
22
16
88160
ab
aabb
⎧
+=
⎨
+=−+=
⎩
,
{
22
16
8 8 16 16
ab
ab
+=
−
+=−
{
22
16
4
ab
ab
+
=
−=−
а) При a = 0; b= 4:
{
22
0416
04 4
+=
−=−
⇒
{
16 16
44
=
−
=−
⇒ решение
б) При a = 0; b= –4:
{
22
0 ( 4) 16
0(4) 4
+− =
−− =−
⇒
{
16 16
44
=
≠
−
⇒ не решение
в) При a = –4; b= 0:
{
22
(4) 0 16
40 4
−+=
−+ =−
⇒
{
16 16
44
=
−
=−
⇒ решение
№1213.
x + y = 5; 2x – y = 16; x + 2y = 3;
{
5
23
xy
xy
+=
+=
⇒
{
5
523
xy
yy
=−
−+ =
⇒
{
7
2
x
y
=
=
−
Подставим в уравнение 2x – y = 16: 2 ⋅ 7 – (–2) = 16 — верно. Тогда все эти
прямые пересекаются в точке (7; –2).
170
№1214.
5x – 2y = 3; x + y = a; (0; y), при x = 0: 5 ⋅ 0 – 2y = 3; y = –1,5;
при x = 0, y = –1,5: x + y = a; 0 – 1,5 = a; a = –1,5.
№1215.
bx + 3y = 10; x – 2y = 4; (x; 0); при y = 0: x – 2 ⋅ 0 = 4; x = 4;
при y = 0, x = 4: b ⋅ 4 + 3 ⋅ 0 = 10; 4b = 10; b = 2,5
№1216.
y = kx – 4; y = 2x – 5; y = –x –1;
{
25
1
yx
yx
=
−
=
−+
,
{
12 5
1
xx
yx
−
+= −
=− +
,
{
2
1
x
y
=
=
−
(2; –1) — точка пересечения, –1 = k ⋅ 2 – 4; k = 1,5.
№1217.
а)
30
4
2
yx
xy
xy
+=
⎧
⎪
−=
⎨
+=−
⎪
⎩
3
4
2
yx
yx
yx
=−
⎧
⎪
=−
⎨
=− −
⎪
⎩
1
5
3
y
x
35
–
5
–
3
–
5
–
3
–
1
L
0
–
1
1
y
=
x
– 4
y
= –3
x
y
= –2 –
x
Ответ: (1; –3).
б)
1
3
20
xy
yx
xy
+=
⎧
⎪
−=
⎨
+
=
⎪
⎩
1
3
2
yx
yx
yx
=−
⎧
⎪
=+
⎨
=−
⎪
⎩
1
5
3
y
x
35
–
3
–
5
–
3
–
1
L
0
–
1
1
y
=
x
+ 3
y
= –2
x
y
= 1 –
x
Ответ: (–1; 2).
