Мошинский Л. Эпоксидные смолы и отвердители
Подождите немного. Документ загружается.

-181-
Стремясь
получть
более
точную
аппроксимацию
кинетических
данных,
Бар·
тон
2О
ввел
допущение,
что
кинетика
отвеРЖДения
амино-эпоксидной
системы
описывается
аВТQкаталитическим
уравнением
первого
порядка,
но
константы
такой
модели
изменяются
симбатно
степени
ОТ8ерждения.
При
ЭТОМ
коэффициенты
уравнения
(4)
имели
следующий
вид:
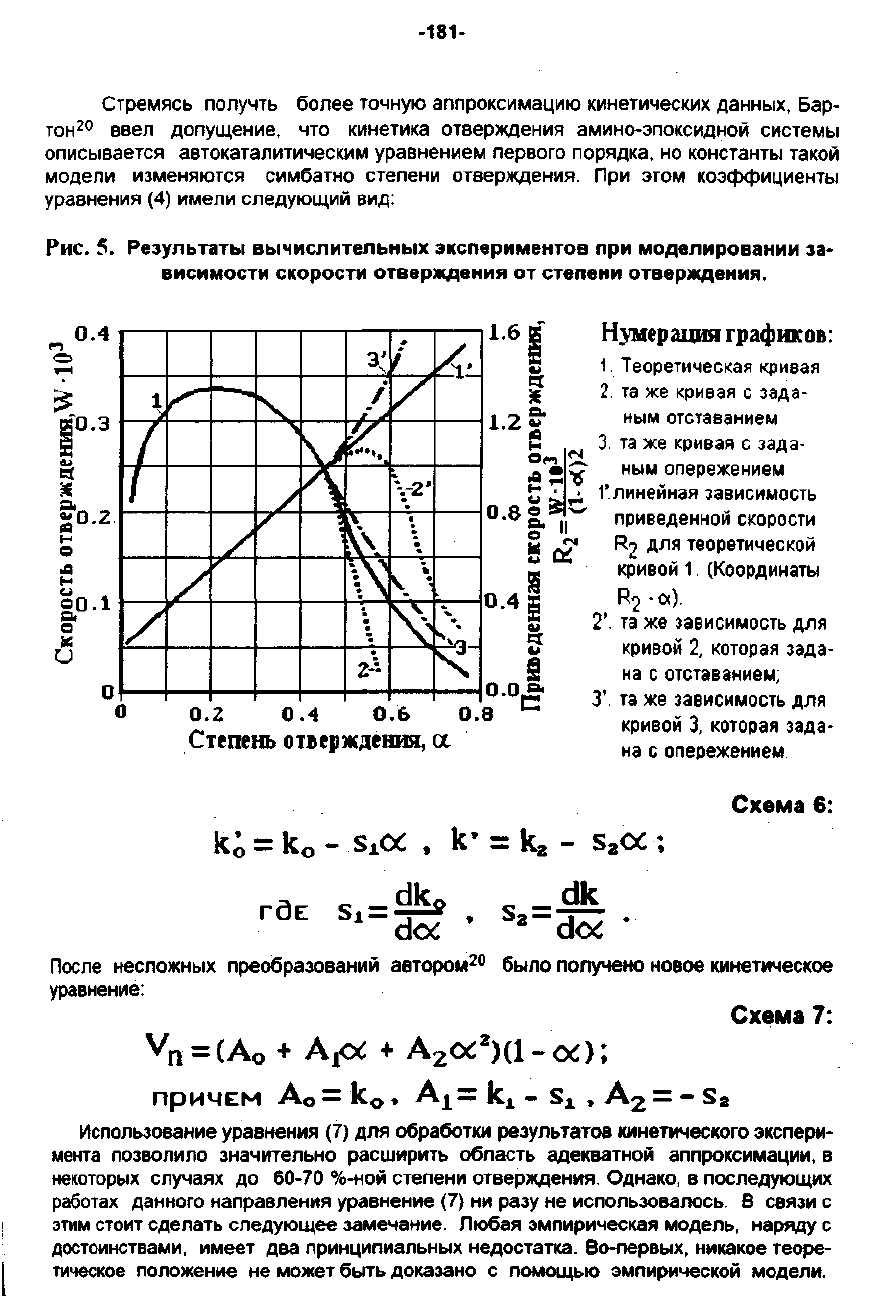
Рис.
5.
Результаты
вычислительных
экспериментов
ПР"
моделировании
за·
8ИСИМОСТИ
скорости
отвер*дения
ОТ
степен"
отвер*дения.
;3:.
~О_З
~
~
...
~O.2
~
..
~
u
1
I
/
/
З'
,
i'..
i
'\
~.
~
t,
\'\
,
V
-<!..
~.-2·
\
-
Г'-
\
1.61
~
Нумерация
rраф""
••
:
1
Теоретическая
кривая
2.
та
же
кривая
с
зада-
1 2
~
НЫМ
отстаВанием
.
:!
~M
З.
та
же
кривая
с
зада
..
м
,Q
_
~
мы
...
опережением
t
':'"
.,.:.
1'.линеЙная
зависимость
0.8
g,
11-
приведенной
скорости
~
rZ
R
2
ДЛЯ
теоретической
iii
КРИВОЙ
1
(Координаты
~o.l
6
0.4
~
R2
.~)
2',
та
же
завиСИМОСТЬ
ДЛЯ
~
КРИВОЙ
2,
которая
зада-
1/
-
К
~:--
-
о
о
-
1"
z.?
!!
0.0ё'
o.z
0.4 0.6
0.8
Степень
0Iвер_дения,
ct
k~
= k
o
- s.oc •
k'
=
k.
dk
o
гдЕ
S.=
doc
•
на
С
отставанием;
З'
тз
же
заВИGИМОСТIo
ДЛЯ
КРИВОЙ
З,
которая
зада-
на
с
опережением
Схема
6:
- SaC<:;
После
несложных
преобраэований
автором
2О
было
получено
новое
кинетическое
уравнение:
Схема
7:
УП=<А
О
+
А
1
ос
+
А
2
ОС')(1-ОС);
ПРИЧЕМ
А
о
= k
o
•
А
1
=
k.
- s
••
А
2
= -
S.
Использование
уравнения
(7)
ДЛЯ
обработки
результаТ08
КИН81'И'4еского
экспери
мента
позволило
значительно
расширить
область
адекватной
аппроксимации,
в
некоторых
случаях
ДО
60-70
%-ной
степени
Qтверждения.
Однако,
в
последующих
работах
данного
направления
уравнение
(7)
ни
разу
не
испольэовалось.
В
связи
с
этим
стоит
сделать
следующее
замечание.
Любая
эмпирическая
модель,
наряду
с
достоинствами,
имеет
два
принципиальных
недостатка.
Во-первых,
никакое
теоре
тическое
положение
не
может
быть
доказано
с
ПОМОЩЬЮ
эмпирической
модели.
-182-
Приведенные
уравнения
являют
тому
пример:
с
теоретической
точки
зрения
параметры,
зависящие
ОТ
степени
отверждения,
неправомерно
рассматривать
как
константы
скорости.
Во-вторых.
эмпирическая
модель
бессмыслена.
если
получа·
емые
результаты
нельзя
использовать
практически.
Практическая
же
ценность
уравнения
(7)
достаточно
сомнительна,
ЧТО
в
каКОЙ-ТО
мере
позволяет
объяснить
причину
неприятия
ЭТОЙ
модели.
Более
практичные
данные
МОЖНО
ПОЛУЧТЬ
с
использованием
эмпирических
моделей
кинетики
типа
уравнения
(8):
Схема
8:
v n = -
~
=
kn(X
o
-
х)п
r
де
V n -
как
и
ранее
СКОРОСТЬ
отверждения,
а
остальное
расшИфровано
в
табли
це
1.5.
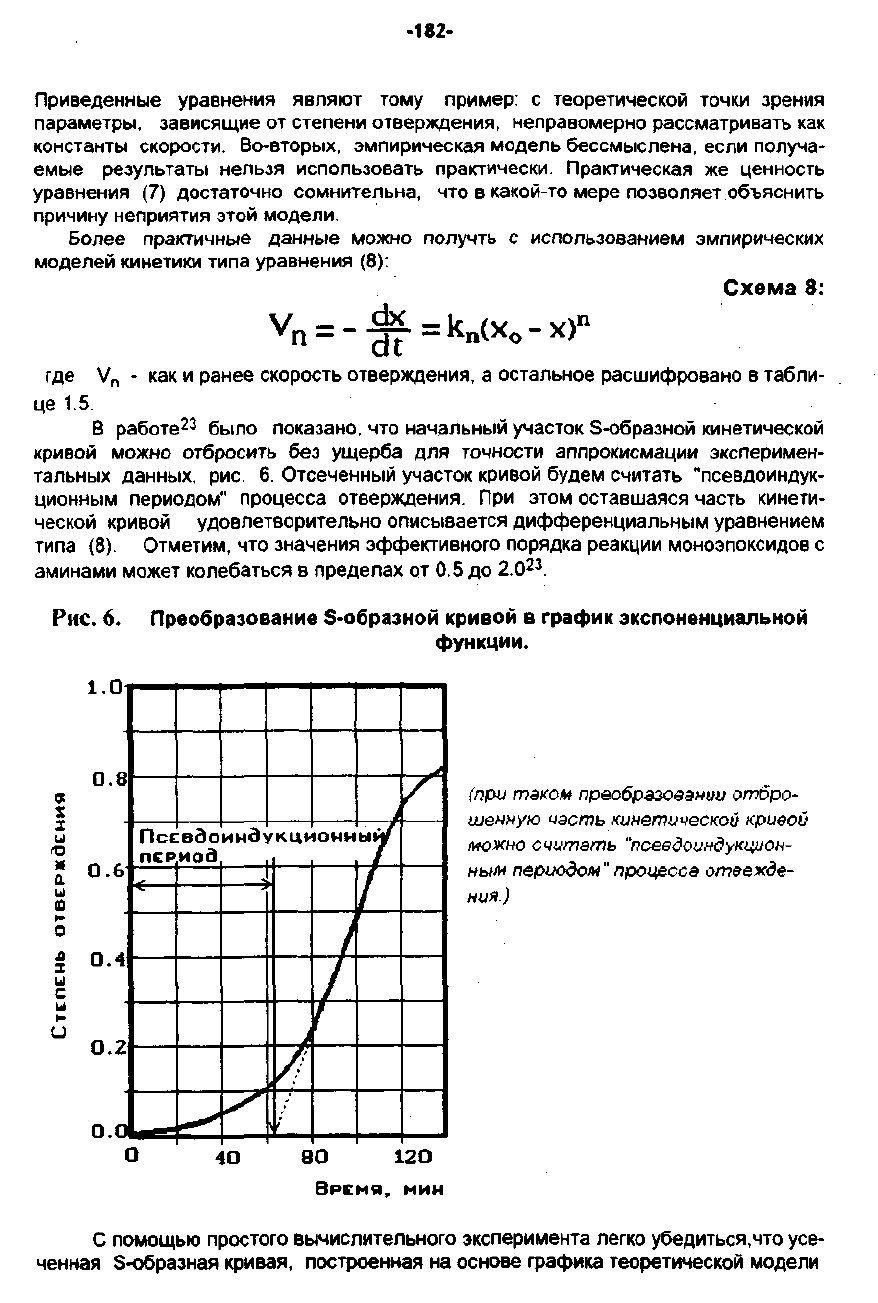
В
работе
23
было
показано,
что
начальный
участок
S-образной
кинетичесКОЙ
КРИВОЙ
МОЖНО
отбросить
без
ущерба
дЛЯ
ТОЧНОСТИ
аппрокисмации
эксперимен
тальных
данных,
рис.
6.
Отсеченный
участок
кривой
будем
считать
Мпсевдоиндук
ционным
периодом"
процесса
отверждения.
При
этом
оставшаяся
часть
кинети
ческой
кривой
удовлетворительно
описываетсЯ
дифференциальным
уравнением
типа
(8).
Отметим,
что
значения
эффективного
порядка
реакции
моноэпоксидов
с
аминами
может
копебаться
8
предепах
от
0.5
до
2.023.
Рис.
6.
ПреобраЗ0вание
S-образной
кривой
в
rрафик
экспоненциальной
1.0
О.
в
•
•
:
"
"
•
О.
•
6
"
•
•
о
•
О.
:
4
"
с
"
•
u
О.
2
О.
о
пс~ваоинаукционн
псриоёl
/
//
/'
40
во
V
ы1
120
функции.
(при
тЭКОМ
преобрЭЗQвэнuu
отбро
шенную
чэсть
кuнетической
кривой
!IЮЖ/-Ю
считать
"nceвдoиндYKЦUOH
ныМ
nepuoдoM"
процессэ
оmеежде
ния.)
BpI:H
....
НИН
с
помощью
простого
вычислительного
эксперимента
легко
убедиться,
что
усе
ченная
S-образная
кривая,
построенная
на
основе
графика
теоретической
модели
-183-
автокаталитической
кривой
второго
порядка,
адекватно
описывается
дифференци
альным
уравнением
(8)
при
n =
1.
8
наших
ра60тах
13
.
25
было
показано,
что
только
уравнение
первого
порядка
дает
адекватное
описание
усеченной
кинетической
кривой.
рис.
7.
При
этом
требуемая
точность
описания
экспериментальных
данных
распространяется
до
80-85 %
конверсии
ЭПОКСИДНЫХ
групп.
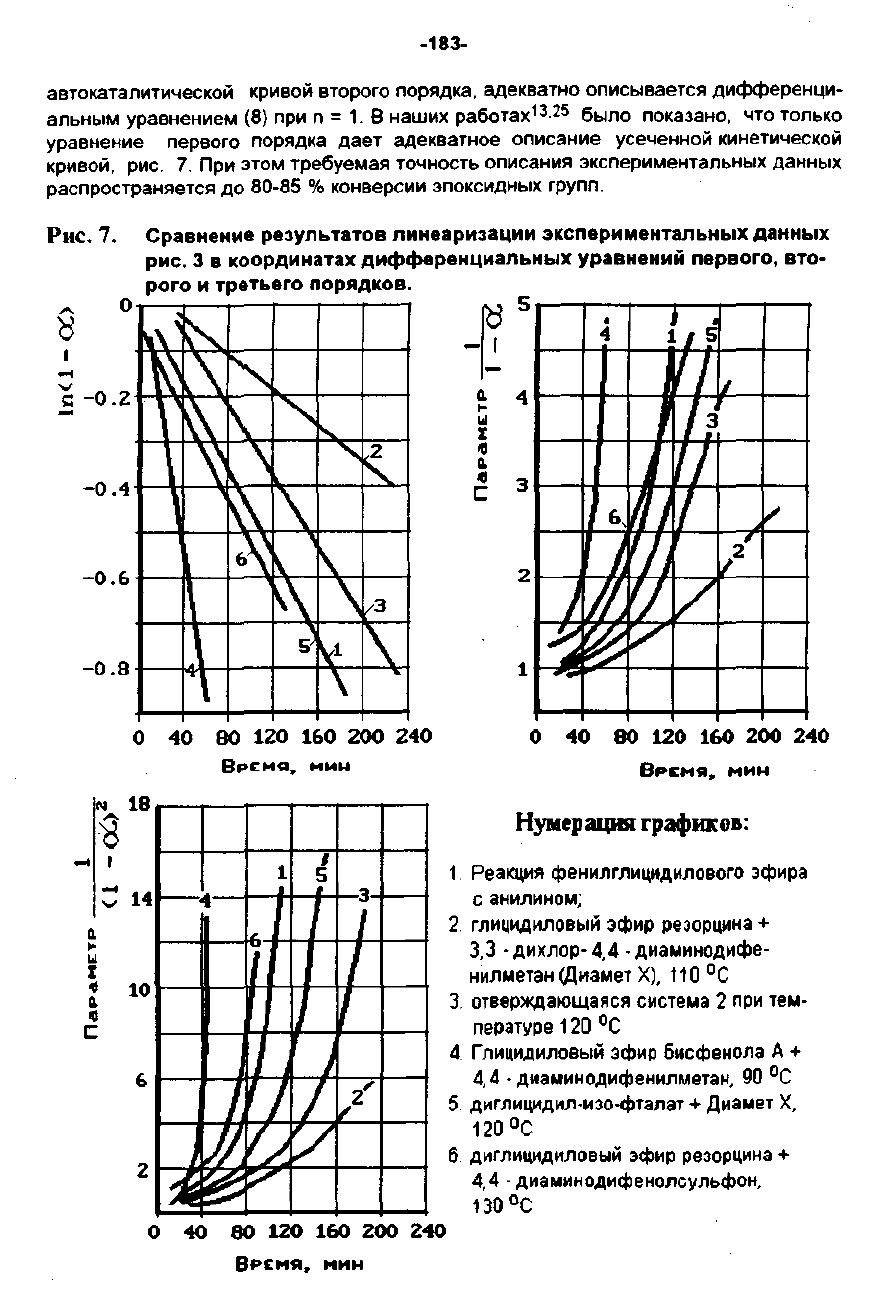
Рис.
7.
Сравнение
результатов
линеаризации
экспериментальных
AaHHblX
рис.
3 8
координатах
дифференциальных
уравнений
первого,
8ТО-
~
v
о
рога
и
третьего
порядков.
~\
~
~
.\
~"
"
С
-O.Z
\
\
r(
1\
-0.4
6
\.
~\
\
з
-0.6
5
"1
\
\
-0.8
о
40
80
120 160
200 240
Bp~HQ~
нии
N
18
.~
~
1
,
5
~
1
v
4Г-4
3
•
•
w
r
•
10
•
•
I
11
1:
6
I J
1/,,2'
2
WII
..
A/
~
о
40
80
120 160
200 240
•
•
w
r
•
•
•
1:
з
,;2
21---1-.
4-I-A---,'1'--!--I
J V
о
40
80
120 160
200 240
НумерaциII
rрафИЕОВ:
Реакция
феНИЛГЛИЦИДИЛО80ГО
эфира
с
анилином;
2.
глицИДиловый
эфир
реэорцина
+
З,з
•
дихлор-
4,4·
диа",инодифе·
нил
...
етан
(Диамет
Х),
t
10
ОС
з.
отверждающаяся
систе
...
а
2
при
те
...
•
пературе
120
ос
4_
Г
лицидилоеый
Эфир
бисфенола
Д
+
4,4
•
диа",инодифенилметан,
90
ос
5_
диглицидил·иэо.фталат
+
диа
...
ет
Х,
120
ОС
б_
диглицидиловый
эфир
реэорцина
+
4,4 .
диаминодифенолсульфон,
130
ос

-184-
Наконец
отметим,
ЧТО
8
работах
27
,28
кинетику
отверждения
зпоксидных
СМОЛ
аминами
было
предложеННQ
аппроксимировать
Т",Н.
уравнением
Asрами.
Собствен
но
уравнение
Аврами
было
введено
для
описания
кинетики
кристаллизации
поли
меров
и
представляет собой
модификацию
дифференциального
уравнения
фор
мальной
кинетики
29
:
Схема
9:
о<:
= 1 -
ехр(-
zt")
,
zt"
=
-In<l
-0<:)
где
«(-
степень
кристаллизации
полимера,Z
-
константа
скорости
кристаллизаЦИИ,m
показатель
Аерами,
зависящий
ОТ
формы
растущих
кристаллов.
Здесь
нет
смысna
обсуждать
применимость
уравнения
Аврами для
описания
кинетики
кристаллизации
полимеров.
Однако,
можно
с
уверенностью
утверждать,
ЧТО
дЛЯ
аппроксимации
данных
кинетики
отверждения
зминоэпоксидныx
систем
это
уравнение
не
пригодно.
ЧТО
было
доказано
в
критическом
обзоре
1З
.
В
заключение
имеет
СМЫСЛ
подчеркнуть, что все
рассмотренные
эмпирические
уравнения
кинетики
являются
частично
аДекватными
моделями,
т.к.
их
использо
вание дает
возможность
описать
лишь
часть
экспериментальной
кинетической
кривой.
С
ЭТОЙ
точки
зрения
наибольшую
точность
описания
обеспечивает
диффе
ренциальное
уравнение
первого
порядка.
Т
акая
модель
неадекватна
в
начальный
период
отверждения
и
на
заключительном
этапе
-
после
80-85
% -
ной
конверсии
эпоксидных
групп.
Остальная
часть
кинетической
кривой
аппроксимируется
точно
и
качество
описания
не
зависит
от
условий
экспериментов
(интервала
температур,
соотношения
компонектов,
концентрации
катализатора
и
других
факторов).
Кинетические
уравнения
авто
каталитической
реакции
также
являются
частично
адекватными
модепями
кинетики
отвеРЖДения
аминоэпоксидных
систем.
При
их
использовании
удается описать
экспериментальные
кривые
на
участке
35-40 %
конверсии.
МЫ
видели.
что
введением
определенных
эмпирических
поправок мож
но
увеличить
соглассованность
таких
моделей.
Однако,
получаемые
при
подобной
обработке
данных
коэффициенты даже
формально
не
MOryf
рассматриваться
как
константы
скорости.
Кииетика
отверждеиия
эпоксидиых
смол
полиаМИН8МИ.
Для
иллюстрации
кинетических
закономерностей
отверждения
эnоксидных
смол
полиаминами
имеет
смысл
воспользоваться
данными
работы
14
,
где
приведены
ре
зультаты
кинетических
эксипериментов
и
продемонстрированы
различные
подходы
к
их
обработке.
В
цитированной
работе
была
исследована
кинетика
отверждения
диглицидилового
эфира
бисфенола
Д
(ДГЭБд)
эвентуально
близкими
производны
ми
диэтиneнтриамина
со
сходными
по
активности
функциональными
группами,
таб
лица
2.5.
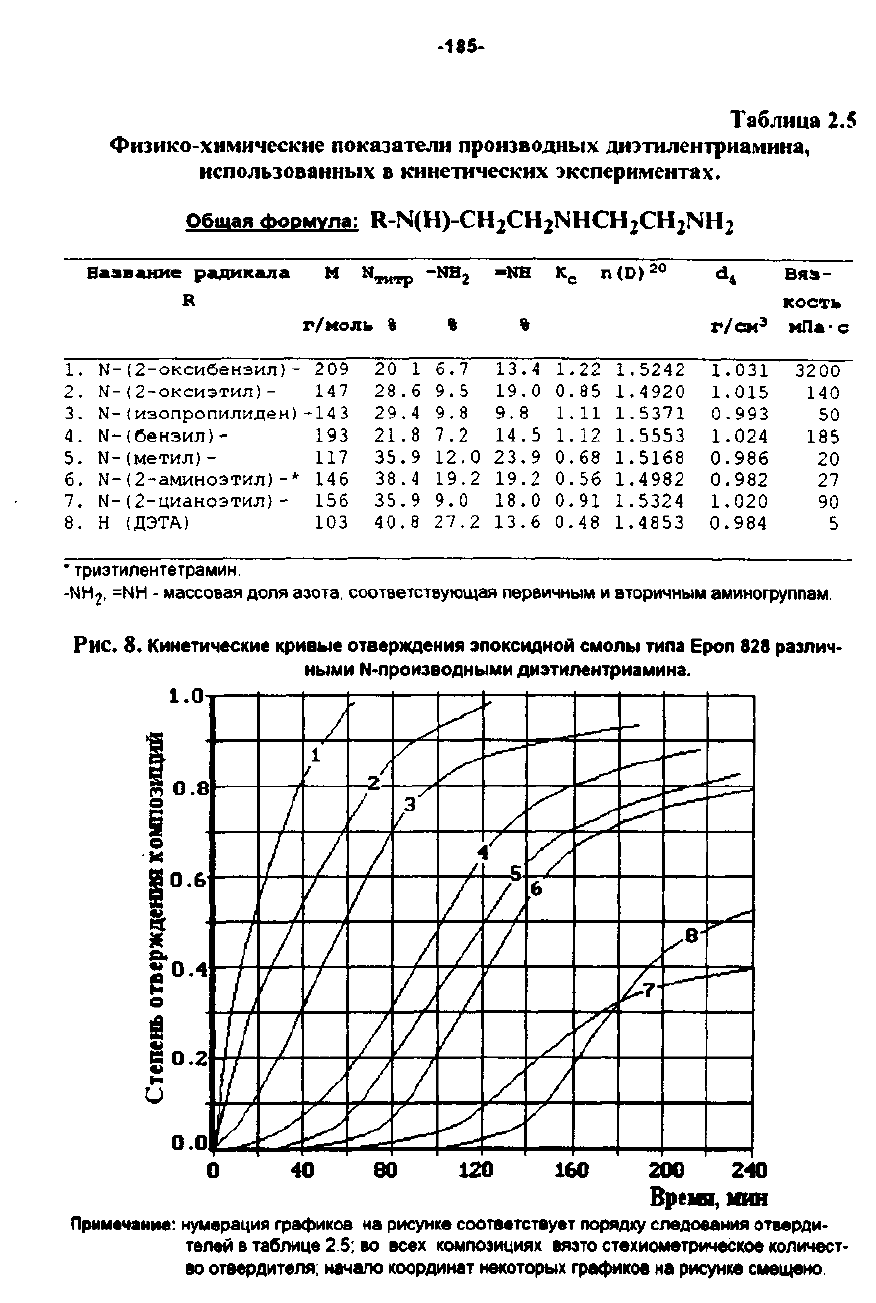
Кинетические
кривыe
отверждения
указанных
систем
лриведены
на
рис.
8.
Интеграпьные
кинетические
кривые
снимали
методом
РОВЭ.
Параллельно
этому,
методом
изотермической
калориметрии
снимали
ДиФФеренциальные
кинетические
кривые.
Статистическая
обработка
экспериментальных
данных
показала,
что
интег
рапьные
кривые
в
пределах
погреwности
эксперимента
совпадали
с
резупь
татами
численного
интегрирования
дифференциальных
кривых.
Подобное
совпадение
де
папо
попученные
данные
ПОЛНОСТЬЮ
сравнимыми
приго.дными
ДЛЯ
обработки
с
ис
пользованием
как
эмпирических,
так и
теоретических
моделей
кинетики.
Это
позво
лило
оценить
адекватность
указанных
моделей
и
сопоставить
точность
описания
экспериментальных
данных.
-185-
Таблнuа
2.5
Физико-химические
показателн
ПРОНЗВОДНLlХ
ДИЭПL1ентриамина,
использованных
8
К'инеmческих
экспериментах.
Об!!l!!~
!l!2RM~n!:
R-N(Н)-СНzСНzNНСН
z
СН
1
NНz
Sаsв&ИИе радикала
Н
Н...."
-NВ,
-NВ
Ко
n
(О)
20
d,
BR!s-
R
ICОСТIo
r/MOI1Io
i
• •
r/с:м
Э
мПа·с
1.
N-(2-0ксибензиn)
209
20
1
6.7
13.4
1.22
1.5242
1.031
3200
2.
М
-
(2
-оксизтил)
-
147
28.6
9.5
19.0
0.85
1.4920
1.015
140
3.
N-tизопропилиден)-143
29.4
9.8 9.8
1.11
1.5371
0.993
50
4.
N-(бенэил)-
193
21.8
7.2
14.5
1.12
1.5553
1.024
185
5.
N-(меТИЛj-
117
35.9
12.0
23.9
0.68
1.5168
0.986
20
6.
N-(2-аминозтил)-*
146
38.4
19.2 19.2
0.56
1.4982
0.982
27
7.
N-(2-циаНQЗТИЛ}-
156
35.9
9.0
18.0
0.91
1.5324
1.020
90
8.
Н
(ДЭТА)
103
40.8
27.2
13.6
0.48
1.4853
0.984
5
•
ТРИЭfиnентетрамин.
·НН
2
.
=НН
•
массоеая
ДОЛЯ
8З0та.
СOQтееТСТ8УЮщая
nepеичным
и
вторичным
аминогруппам.
Рис.
8.
Кинетические
кривwе
отверждения
~ПОКСМДНОIl
смолы
типа
Ера"
828
раmич
ными
N-производными
диатиneнтри"мина.
1.0
/
/'
1
/"'
f-
.--
?/
/'
~
I
v
з/
,/
V
/ I
/
4
//
1/
/ 1/
6
/ / / /
1/
V
8
1/
/
/
;:7
ij
/
/
/
V
L 7
/
/ / / / /
/~
/'
./
V
.---
200
240
Вр"....,
JIIOI
"рим.чан",:
нyt,Iерация
графИIC08
на
рисунке
СООТМТСТ8ует
nopядICy
CЛ8,Q088МИЯ
отирди-
0.0
о
40
80
120
160
те"""
в
таблице
2.5;
80
всех
КОМn03ИЦИЯХ
IЯ3то
стехиометрмческое
количест-
80
отаердителя;
..-чало
координат
некоторых
грефиК08
на
рисунке
с_щеlЮ.
·116-
Согласно
Данным
рис.
8,
ДЛЯ
случая
отверждения
ДГЭБА
оксиэтилированным
и
оксибензилированным
дэтд
характерны
кинетические
кривые
параболического
ТИ~
па.
Подобного
рода
зависимости
в
принципе
МОЖНО
аппроксимировать
без
усечения
и
дЛЯ
ЭТОГО
подходит
дифференциальное
уравнение
первого
порядка
(СМ.
таблицу
1
5).
В
остальных
случаях
были
получены
S-образные
кинетические
кривые.
Оба
типа
зависимостей
аппроксимировались
уравнениями
автокаталитической
реакции
первого
и
второго
порЯДКОВ,
в
форме
удобной
для
обработки
экспериментальных
данных.
Напишем
ЭТИ
уравнения
еще
раз
для
модели
первого
(а)
и
второго
(Ь)
по·
рЯДКОВ:
Схема
10:
(Здесь
штрихи опущены,
а
нижние
индексы
даны
8
удобном
ДЛЯ
обсуждения
мате
риала
виде.)
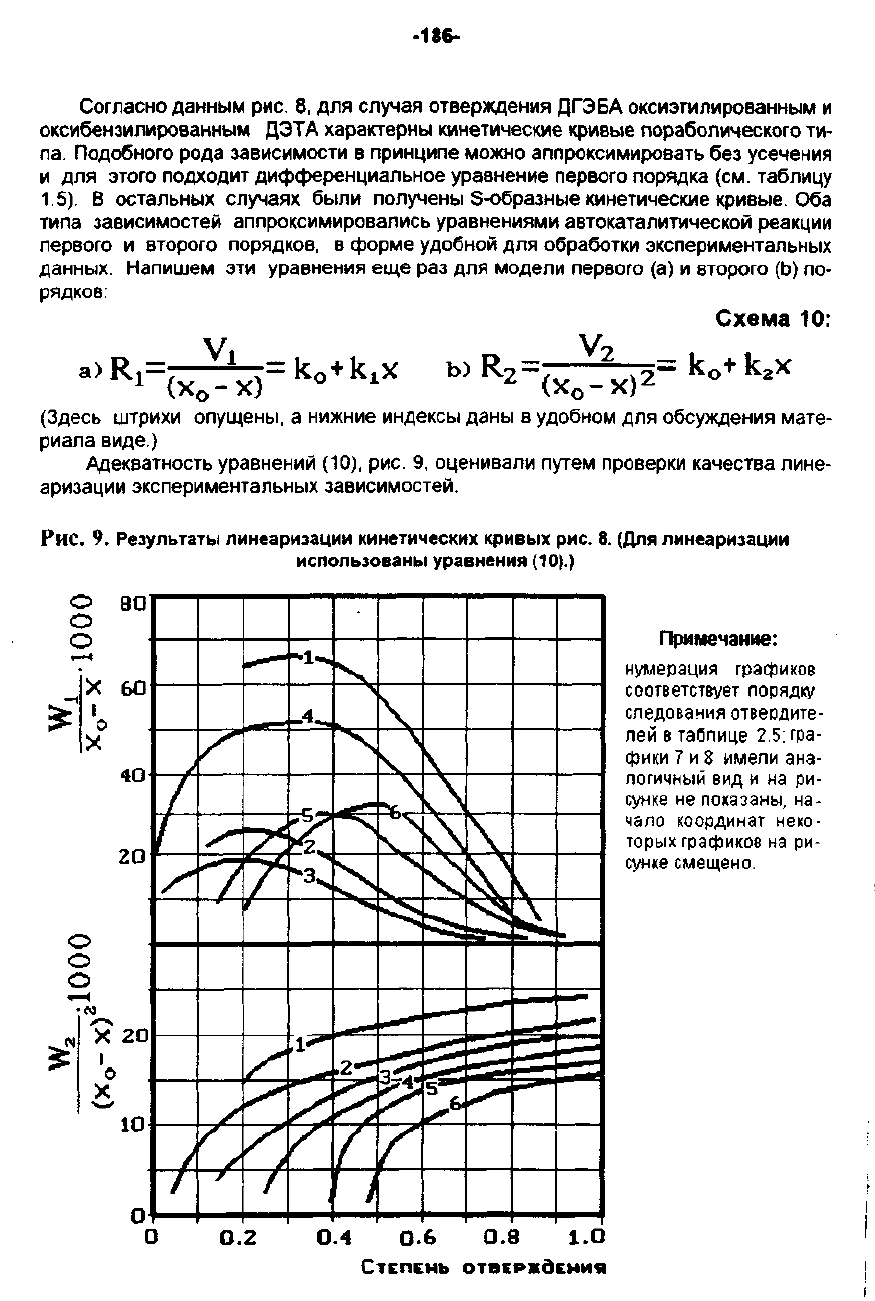
Адекватность
уравнений
(10),
рис.
9,
оценивали
путем
проверки
качества
лине
аризации
экспериментальных
зависимостей.
Рис.
9.
РезультаТ,"1
линеаризации
кинетических
кривыx
рис.
8.
(д.nя
линеаризации
использованы
уравнения
(10).)
о
о
о
.....
х
~
I
О
Х
о
о
о
.....
'N
~
во
60
40
20
Х
20
~"
I
О
Х
~
10
о
о
v
I
1
.....
/'
/'
I /
/"
,/
I
/
I
,
I
0.2
'1~
r-.
4
"-
7z
'"
3
...
~
l'
2-
v
~
V
11
0.4
"\..
"-
'\
\
~
'~
"
~'
'"
~
~
~
>-
~
/'
0.6
0.8
1.0
Ilpммечзнме:
нумерэция
ГРЭФИКОВ
соответствует
порядk'y'
следова'"lИЯ
отвеDдите·
лей
в
таМице
2.5:
гра·
фики
7
11
8:
имели
ана·
логичный
вид
и
на
РИ'
сунке
не
показаны,
на
чало
координат
неко·
торых
графиков
на
ри
сунке
смещено.
-187-
Согласно
приведенным
результатам,
автокаталитическое
уравнение
первого
порядка
в
принципе
не
может
быть
использовано
ДЛЯ
обработки
кинетических
ДЗННЬJХ,
Экспериментальная
зависимость,
построенная
в
КООрДинатах
R
2
-
(1.,
также
не
может
быть
отнесена
к
хорошо
линеаризуемым
моделям.
Тем
не
менее,-
в
чем
летко
убедиться,-
с
использованием
начальных
участков
таких
преобрззованных
КрИВЫХ
МОЖНО
рассчитать
и
"каталитическую"
и
"некаталитическую"
константы
ско
рости
отверждения.
К
сожалению,
подобные
расчеты
ничего
не
значащих
констант
нередко
можно
встретить
в
научных
работах.
Иногда интегральные
формы
автокаталитических
моделей
не
столь
чувствитель
ны
к
отклонениям
Данных
эксперимента
от
теоретической
кривой.
Отметим,
что
приведенные
в
таблице
1.5
интеrральные
формулы
весьма
сложны
и
не
удобны
для
обработки
экспериментальных
данных.
Упростить
указанные уравнения
можно,
положив,
что
(k
o
+k
1
.c
o
>
М
k
1
.c
O
'
а
выражение
tn(k
o
+k
1
x)
М
tn(k
1
x).
С
учетом
указан-ных
упрощений
быпи
получены
удобные для
обработки
данных
приближенные
ки-нетические
уравнения:
Схема
11:
По
нашему
опыту,
уравнения
(11)
часто
обеспечивают
линеаризацию
лучшеrо
ка
чества
даже
в
тех
случаях,
коrда
обработка
данных
с
использованием
дифферен
циальной
формы
уравнений
(10)
дает
типичные
кривые.
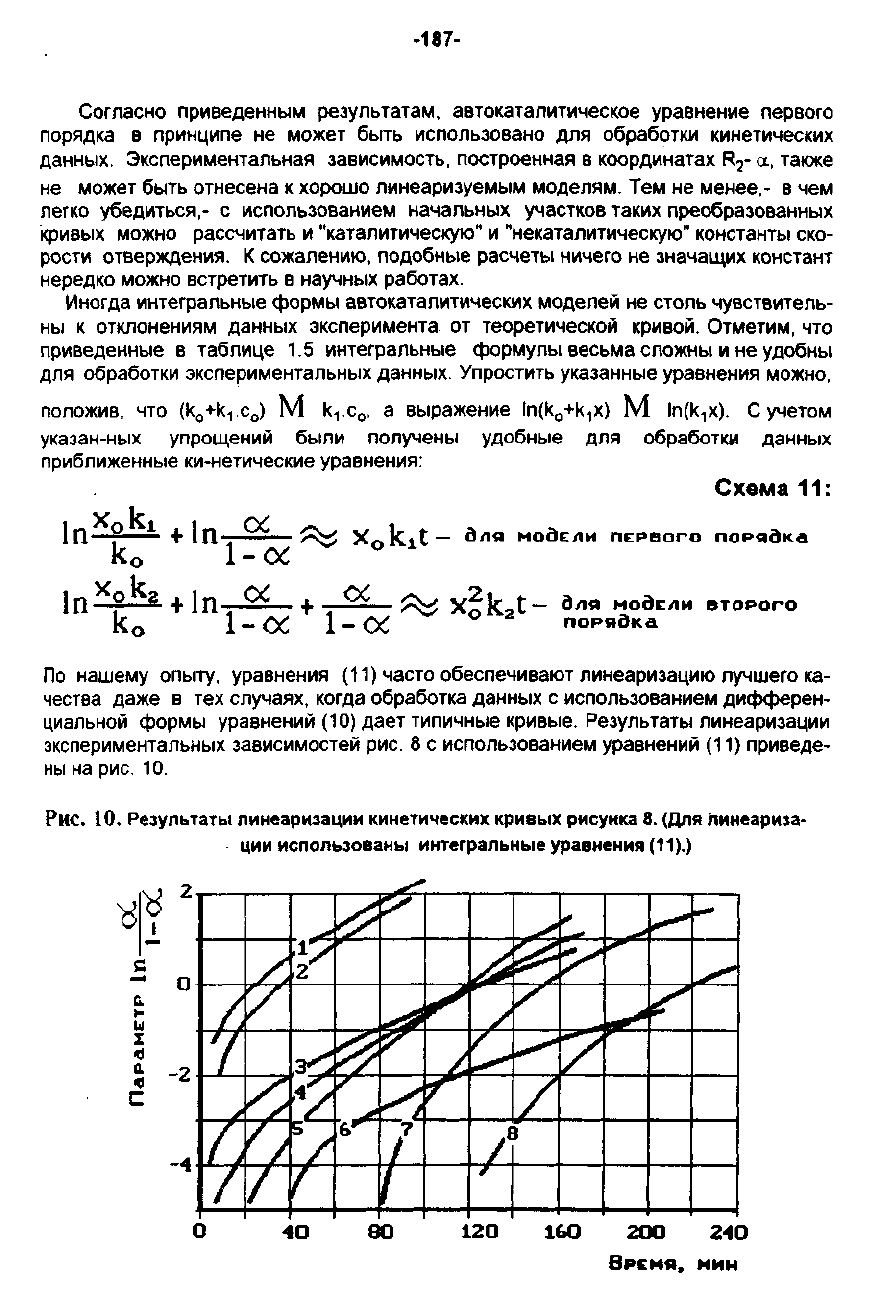
Результаты
линеаризации
зкспериментальных
зависимостей
рис.
8
с
использованием
уравнений
(11)
приведе
Hbl
на
рис.
10.
Рис.
10.
Резуnьтаты
nинеаризации
кинетических
КРИ8ЫХ
рисунка
8.
(Для
hмнеаризз
ЦМИ
ИСПОnЬЗО8аН,,"1
интеrральные
уравнения
(11).)
'Й
2
"
~
v
....
1-
~
...
С
-
О
•
•
"
I
•
•
-2
•
с:
-4
/.
~/
~~
~
,.
/
V
~
v
~
!/'
V
/'
v.,
4/
~
~
/
6"'"
If
V
J
Г'/
Г-/
/8
1/
1/
~
IJ
о
40
80
120
160
200
240
·188-
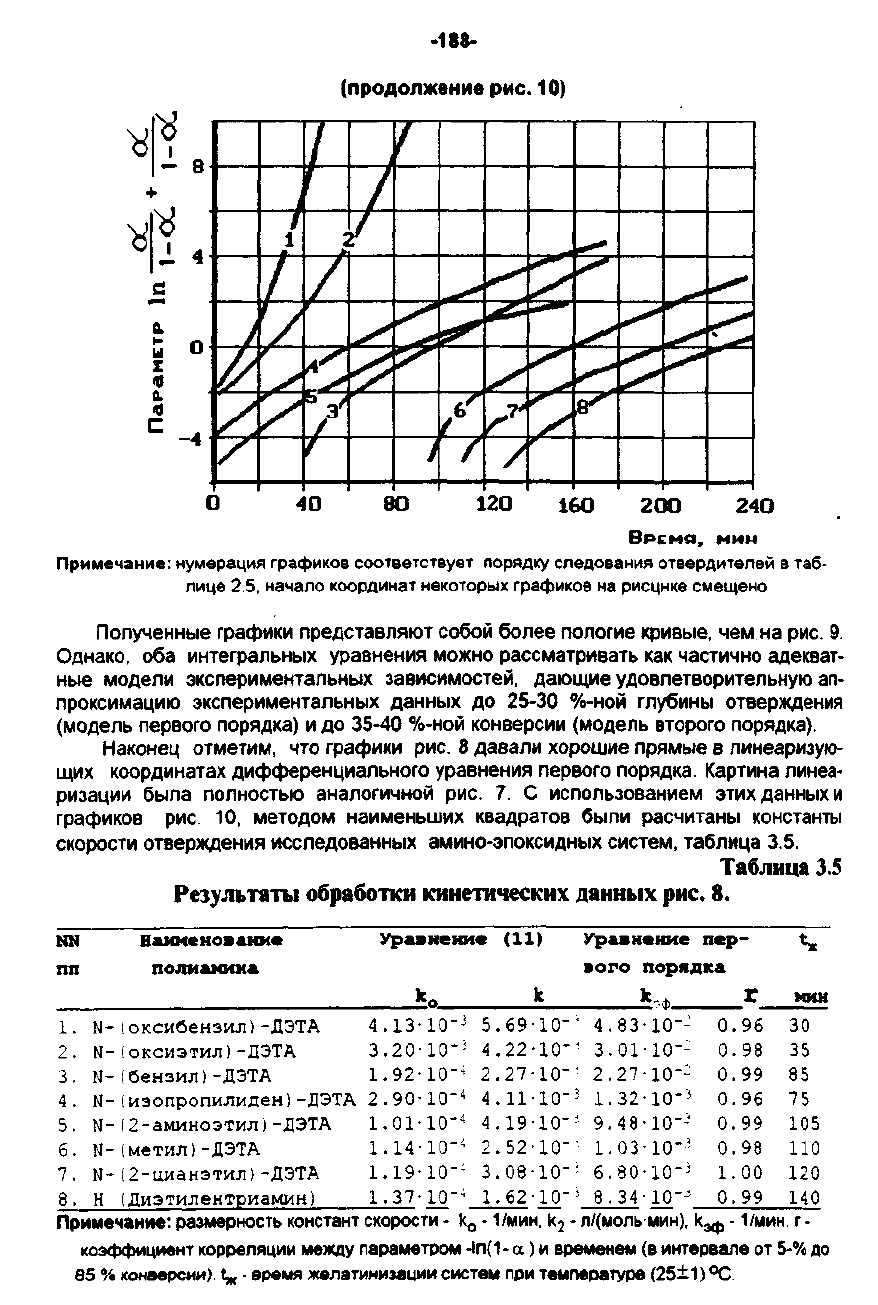
(продол.ение
рис.
1
О)
~I~
8
+
~~
4
-
=
-
•
•
о
w
•
•
•
•
с:
--4
I
If
/
1
V
....
1/
/
,..
у
l'
...
..".
/
./
V
.....
,..
....
~
//
---
..-:
/"
.....
""
v
~
v
,/
;,-
i
/,'
~7"
,-
,.,
/
I
/
о
40
80
120
160
200
240
BPILMQ.
МИ'"
Прммечание:
нумерация
графИКОВ
соответствует
порядку
следования
отвеРДитвпей
в
таб·
лице
2.5.
начало
координат некоторых
графиков
на
РИСЦНКВ
смещено
Полученные
графики
представляют
собой
более
пологие
кривые,
чем
на
рис.
9.
Однако.
оба
интегральных
уравнения
можно
рассматривать
как
частично
адекват
ные модели
экспериментальных
зависимостей,
дающие
удовлетворительную
ап
проксимацию
экспериментальных
данных
ДО
25-30
%-НОЙ
глубины
отверждения
(модель
первого
порядка)
и
ДО
35-40
%-НОЙ
конверсии
(модель
второго
порядка),
Наконец
отметим,
что
графики
рис.
8
давали
хорошие
прямые
в
линеаризую
щих
координатах
дифференциального
уравнения
первого
порядка.
Картина
линеа·
ризации
была
полностью
аналогичной
рис.
7.
С
использованием
этих
данных
и
графиков
рис.
10,
методом
наименьших
квадратов
были
расчитаны
константы
скорости
отверждения
исследованных
амино-эпоксидных
систем,
таблица
3.5.
ни
nn
1.
2.
3.
4.
5.
6.
7.
8.
Таблица
3.5
РезУJlЬТ811d
обработки кинетическнх
данных
рис.
8.
ВаимеН08аим..
Ур
..
меки.
(11)
Ур"н.кие
nep-
t,.
.onи_
801"0
пор.дка
Ж.
k
k_.
ф
r
мин
N-(оксибензил)-ДЭТА
4,13'10-3
5.69'10--
4.
8З-10-~
0.96
30
N-(оксиэтил)-ДЭТА
3.20'10-3
4.22
-10-'
3.01'10--
0.98
35
N-(бенэил)-ДЭТА
1.92-10-4
2.27-10--
2.
27
'10-~
0.99
85
N-(изопропилиден)-ДЭТА
2.90-10-4
4.11'
10-3
1.32-10-'
0.96
75
N-(2-аминоэтил)-ДЭТА
1.01-10-4
4.19
'10-
.
9.48·10-~
0.99
105
N-
(метил)
-ДЭТА
1.14·10-~
2.52
.
10-
1.03-10-~
0.98
110
N-(2-цианэтил)-ДЭТА
1.19-10-~
3.08'
10-
:
6.80-10-)
1.00
120
Н
(Диэтилентриамин)
1.
37-10-~
1.62
.
10-
,
8.34'10-.0
0.99
140
-
----
----
"риме
..
а"
...
:
размерность
констант
скорости
-
~.
1!мин.
k
2
-
л!(моль·мин).
kэф
-
1/МИн.
г-
коэффициент
корреляции
между
П8раметром
4П(1-
а)
и
временем
(8
интервале
от
5--%
ДО
65
%
конеерсни).
t,..
-
время
желатиии"'ЦИИ
систем
при
т_neратуре
(25±1)
ОС.

"189-
Анализ
приведенных
в
таблице
3.5
результатов
показал,
что
рассчитанные
с
ис
пользованием
разных
моделей
константы
скорости
существенно
различаются
по
величине,
имеют
разную
размерность
и
слабо
коррелируют
между
собой,
хотя
рас
читаны
с
использованием
одних
и
тех
же
экспериментальных
данных.
ИЗ
этого
следует,
что
такие
константы
-
это
эмпирические
коэффициенты,
которые,
в
ПРИН
циле,
МОЖНО
использовать
для
сравнения
кинетики
отвеРЖДения
узкого
круга
одно
типных
композиций.
Однако,
такие
данные
не
достаточны
для
обобщения
теорети
ческих
предстзвлений
о
процессе
и
не
MOryт
обеспечить
исчерпыеающеrо
описания
кинетики
отверждения
амино-эпоксидных
(и
других)
систем.
Для
сравнения
можно
привести
результаты
обработки
тех
же
экспериментальныx
данных
рис.
8
с
помощью
теоретической
модели
кинетики.
Такое
уравнение
было
получено,
исходя
из
конструктивной
модели
механизма
отверждения,
которая
была
уже приведена
в
предыдущей
главе.
Для
УДОбства
напишем
этот
короткий
меха
низм
еще
раз:
Схема
12:
-
~ЕКdТdnИТИЧЕСКdЯ
РЕdКЦИЯ
ОКСИdnКИnИРОВdНИЯ
пrрвичнои
dНИ~ОГРУППЫ
-Н'-СН-
СН
2
, "
+
О
)
-Н'-СН-СН2-НН-Н
I
ОН
-
СИСТЕНd
активирующих
Рd8НОDIO:СИИ
Я""ОН
СН
н/Н-
,,=="'>
Г
Н
"_О9]
+
[-СН2-Нн+'~сЯн-г_l
+ -
.г
'СН2-
~
~
J
-Н'-СН- СН
2
'о
/я-
+
-сн.-н
"СН2-
катализироваННЫЕ
РЕакции
ПОnИНЕробразования
[-И'-;~Н.
]
+
II-Юb
)
["и'
-t"сн.-~и]
[-и"
-СН-СНг
]
["и'_сн-сн._k'и-
j
~
00
+
-CН2-rtН-H
)
I I
"ОЬ
ОН
Н
[-и'
-СН-СНг
]
[и,,-ое]
-R'-al-al2-0-R"
"
.'
+
)
+ОН
I
ОН
Рассмотрим
наиболее
простой
случай,
когда
реаlЩИЯ
гомополимермзации
эпок
сидных
групп
не
протекает,
а
активность
neрвичной
и
вторичной
аминогрупп
в
реакциях
оксиалкилирования
одинакова.
В
работе
49
было
подтверждено
соответ
ствующими
топологическими
расчетами,
что
подобное
упрощение
не
должно
оказывать
влияния
на
резуль
таты
кинетических
экспериментов.
С
учетом
сказан
ного,
теоретическая
модель
макрокинетического
закона
отверждения
амино-эпсж
сидной
системы
должна
иметь
следующий
вид:
·190-
Схема
13:
где
(со-х)
-
текущая
концентрация
ЭПОКСИДНЫХ
групп,
I
NR
з
1-
концентрация
атомов
азота,обладающих
свойствами
основаНИЯ.
Остальное
расшифровано
на
схеме
(12).
Уравнение
(13)
неудобно
ДЛЯ
математической
обработки
Данных
кинетического
эксперимента,
но
его
можно
упростить,
если
учесть
следующие
соображения.
КОН
станты
ОСНОВНQСТИ
ЭПОКСИДНОЙ
группы
И
амина,
по
крайней
мере
ДЛЯ
условий
вод
ного
раствора,
имеют
следующий
десятичный
Порядок:
Схема
14:
•
дnя
ЭПОКСИДНОЙ
rруппь
•..................
",О
К'
= 10-9
-
для
алифатических
полиаминов
К"
= 10-5 _ 10-4
ЯСНО,
что
отношение
(К'/К")
может
служить оценкой
значения
константы
К
2
.
т.е.
К
2
М
10-5
-
10-4
С
другой
стороны,
концентрация
аминогрупп
сравнима
с
начальной
концентрацией
эпоксидных
групп.
Следовательно,
для
условий
отверждения
в
блоке
I NR)
1»
К
2
(с
о
·х).
С
учетом
этого,
формула
(13)
приобретает
следующий
удобный
для
математической
обработки
вид:
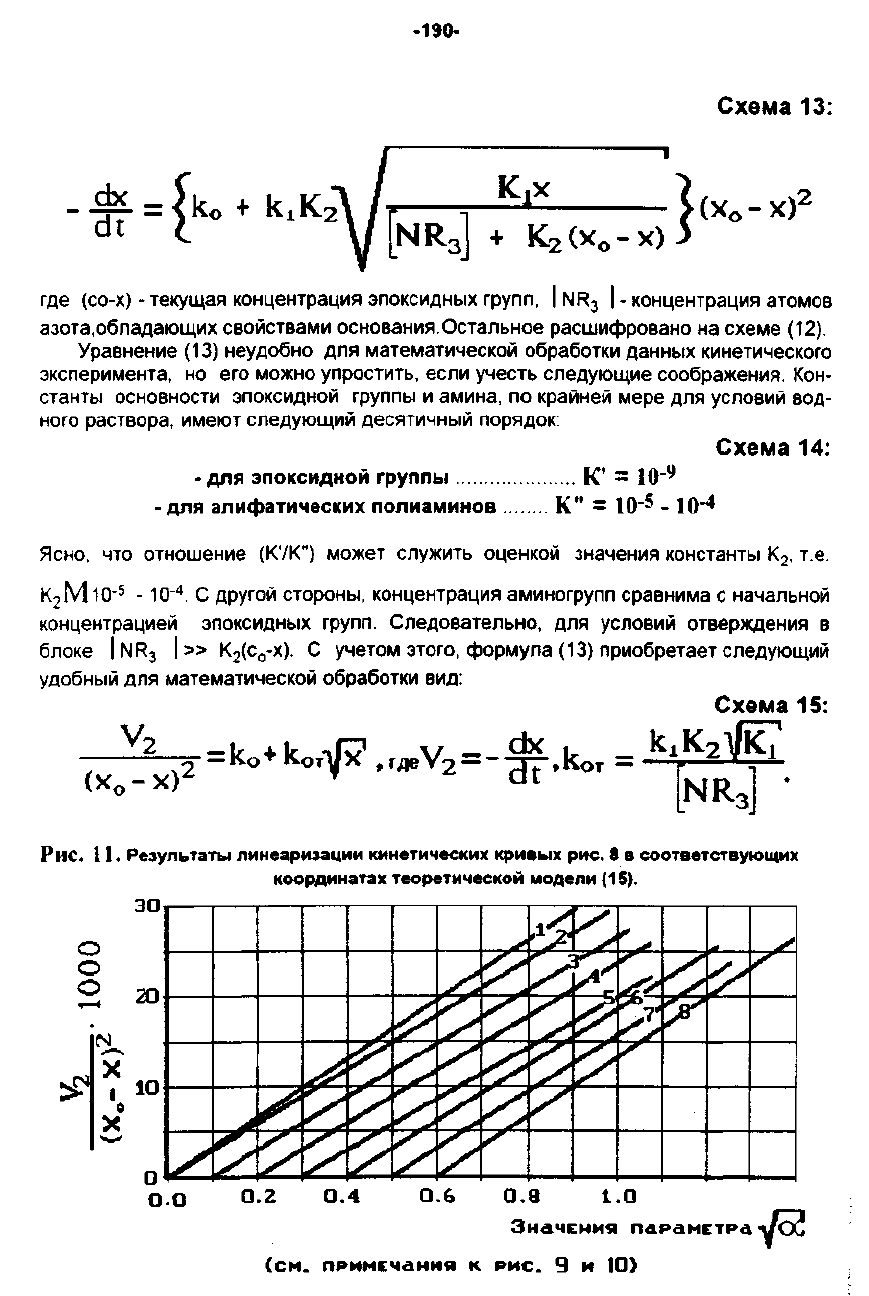
Схема
15:
V
z
-k
+k
,Гv'
V
dx
k
k.K
z
К
1
2 -
о
от,х
,где
2=-dt,
ОТ
= ]
(хо-х)
NR
з
.
Рис.
11.
Резул"таты
линеаризации
кинетических
kpи
....
х
рис.
8
в
соответствующих
кооРДМнатах
теоретической
модели
(15).
о
о
о
.....
30
20
1/
1~
V
..
./
V V
~
..
/"
V.
'l
~
.....
./
~
....
/
I::?
v:
р"
~
~
v
~
~
t/
~v
v v
v"
~
V
~ ~
~
~
с,...
'/
0.2
0.4
0.6
0.8
1.0
ЭН4ЧЕниg
П4раМЕтра..у<Х.
(СМ.
ПРММЕЧdНМЯ
к РИС.
9 "
10)
