Мота А.Н. Конспект лекций по начертательной геометрии
Подождите немного. Документ загружается.

42
На эпюре одноименные проекции пересекающихся прямых
пересекаются, и точки их пересечения лежат на одной линии
связи. На рис. 39, а дано наглядное изображение пересекаю-
щихся прямых: а I b = K, а на рис. 39, б — их чертеж в ортого-
нальных проекциях:
()
21
2
2
2
1
1
1
, KKKba
Kba
Kba
=⇔
⎭
⎬
⎫
=
=
I
I
I
— точка пересечения прямых.
Одноименные проекции параллельных прямых параллельны
между собой (рис. 40, а и б
):
⎩
⎨
⎧
⇔
.d||c
d||c
d||c
22
11
;
z
y
Î
x
p
2
p
1
d
c
d
1
c
1
d
2
c
2
c
2
d
2
c
1
d
1
а б
Рис. 40
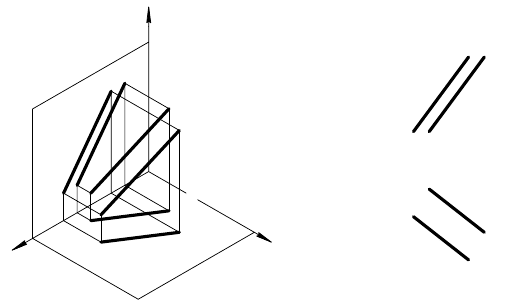
Одноименные проекции скрещивающихся прямых на эпюре
могут пересекаться, но точки их пересечения не лежат на одной
линии связи (рис. 41, а и б
) или одна пара одноименных про-
екций — параллельные прямые: m
1
|| n
1
(рис. 42), а вторая пара
одноименных проекций — пересекающиеся прямые: m
2
I n
2
.
Проецирующие плоскости α и β, образованные при проеци-
ровании прямых m и n на плоскость π
1
, параллельны между со-
бой и пересекают плоскость π
1
по параллельным прямым:
m
1
≡ h
0
α
≡ α
1
||
n
1
≡ h
0
β
≡ β
1
.
43
z
y
Î
x
p
2
p
1
a
a
2
b
2
b
b
1
a
1
4
3
3
2
≡
4
2
3
1
4
1
1
2
2
2
1
1
≡
2
1
1
2
3
1
4
1
1
2
2
2
b
1
a
1
b
2
a
2
3
2
≡
4
2
1
1
≡
2
1
а б
Рис. 41
Скрещивающиеся прямые проецируются на плоскость про-
екций в параллельные прямые m
1
||
n
1
в том случае, если плос-
кость ε параллельная прямым m и n является проецирующей
(рис. 42, а). Во всех других случаях скрещивающиеся прямые
проецируются в пересекающиеся прямые m
2
I n
2
(рис. 42, а),
так как проецирующие их плоскости пересекаются: γ I δ.
p
2
x
y
z
p
1
b
m
2
1
2
≡
2
2
n
2
1
2
a
m
n
e
m '
n '
1
1
2
1
m
2
n
2
1
1
2
1
m
1
≡
h
0
a
≡
a
1
n
1
≡
h
0
b
≡
b
1
d
g
n
1
≡
h
0
b
≡
b
1
1
2
≡
2
2
m
1
≡
h
0
a
≡
a
1
а б
Рис. 42
44
3.2. ТЕОРЕМА ОБ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ
ПРЯМОГО УГЛА
Частным случаем пересекающихся прямых являются пер-
пендикулярные прямые. Прямой угол, как и любой другой (ост-
рый или тупой) плоский угол, проецируется на плоскость про-
екций без искажения, если образованная его сторонами плос-
кость параллельна плоскости проекций (см. 1.5., св-во 2 б
).
Кроме того, прямой угол проецируется без искажения и в слу-
чае, предусмотренном следующей теоремой.
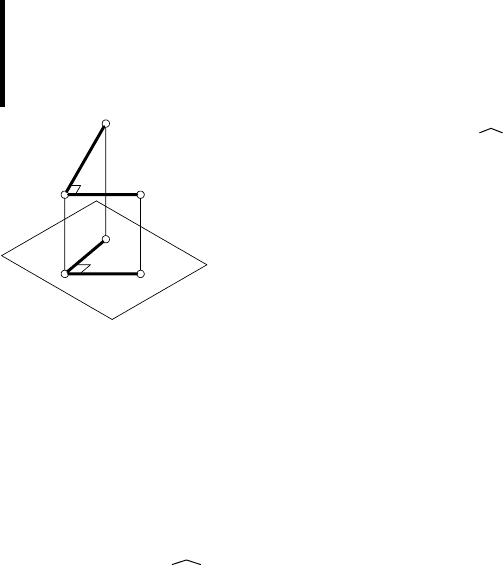
Теорема. Если одна из сторон прямого угла параллельна плоско-
сти проекций, а другая ей не перпендикулярна, то прямой угол
проецируется ортогонально на эту плоскость проекций без ис-
кажения (прямым углом).
Пусть угол между прямыми (АВ) и
(АС
) прямой (рис. 43): ВАС = 90°. Одна
из сторон этого угла, например АС, парал-
лельна плоскости проекций π
1
, а вторая
АВ, ей не перпендикулярна (если бы АВ
была перпендикулярна π
1
, то ∠
ВАС
спроецировался бы на π
1
в прямую ли-
нию). Спроецируем ортогонально АВ и АС
на плоскость π
1
. Проецирующие плоско-
сти АВВ
1
А
1
и АСС
1
А
1
образуют двугранный
угол, ребро которого АА
1
⊥
π
1
. Угол В
1
А
1
С
1
,
ортогональная проекция угла ВАС на плоскость π
1
, является ли-
нейным углом этого двугранного угла (А
1
В
1
⊥ АА
1
и А
1
С
1
⊥ АА
1
).
Проецирующие плоскости АВВ
1
А
1
и АСС
1
А
1
взаимно перпен-
дикулярны. Отрезок [АС
) перпендикулярен данному отрезку
[АВ] (по условию) и проецирующему лучу [АА
1
), т. е. отрезок АС
перпендикулярен плоскости АВВ
1
А
1
. Поэтому проецирующие
плоскости данных отрезков [АВ] и [АС
] взаимно перпендику-
лярны и линейный угол В
1
А
1
С
1
образованного ими двугранного
угла — прямой:
В
1
А
1
С
1
= 90°.
При построении на эпюре прямого угла за одну из его сто-
рон берут горизонталь h или фронталь f (см. 2.6.).
Рис. 43
p
1
C
C
1
A
A
1
B
1
B
45
3.3. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЭПЮРЕ
Плоскость на эпюре задают проекциями геометрических об-
разов, которые однозначно определяют ее положение в про-
странстве:
а) трех различных точек, не принадлежащих одной прямой
(рис. 44, а и б
);
p
2
x
y
z
C
2
A
2
C
2
C
1
p
1
B
2
A
1
C
1
B
1
a
B
a
( A , B
,
C )
B
2
A
2
A
1
B
1
A
C
а б
Рис. 44
б) прямой и не принадлежащей ей точки (рис. 45, а и б
);
Î
p
2
x
y
z
p
1
m
1
m
m
2
C
2
C
1
g
C
m
2
m
1
C
2
C
1
g
( m
,
C )
а б
Рис. 45
46
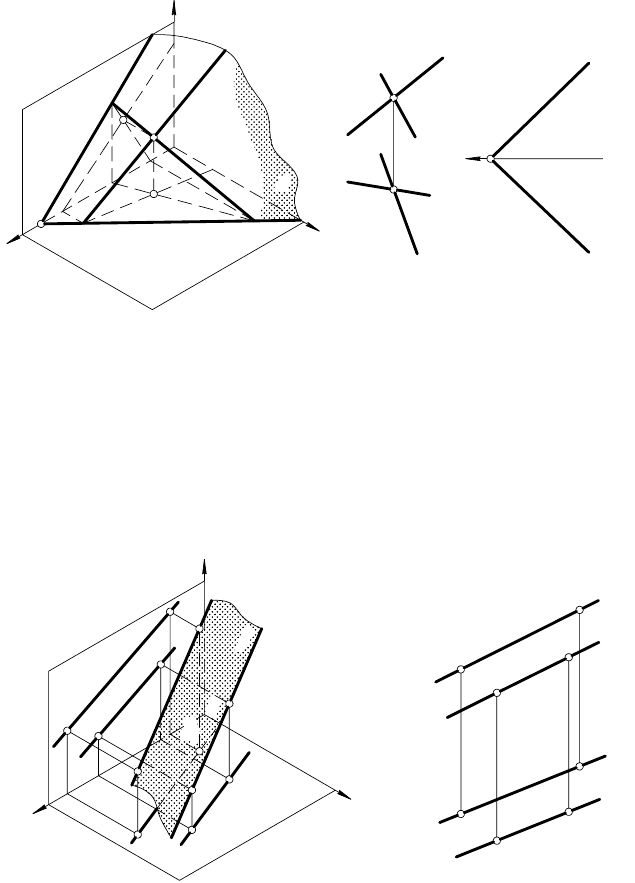
в) двух прямых, пересекающихся в собственной точке
(рис. 46, а, б и в).
Î
p
2
x
y
z
p
1
x
X
a
a
X
a
h
0
a
f
O
a
a
a
1
K
b
K
2
b
2
b
1
a
2
K
1
a
1
K
2
a
2
b
2
b
1
h
0
a
≡
h
0
a
1
f
0
a
≡
f
0
a
2
f
0
a
1
≡
h
0
a
2
K
1
a
( f
0
a
I
h
0
a
)
а б в
Рис. 46
На рис. 46, а дано наглядное изображение плоскости α
, за-
данной пересекающимися прямыми а и b, а I b =К, а на рисун-
ке 46, б даны проекции пересекающихся прямых:
⎩
⎨
⎧
=
=
⇔=
,Kba
;Kba
Kba
222
111
I
I
I
определяющих положение плоскости α на эпюре.
Î
p
2
x
y
z
p
1
D
2
B
2
B
B
1
b
D
D
1
C
1
C
2
A
2
A
A
1
C
B
2
D
2
A
2
C
2
D
1
B
1
A
1
C
1
а б
Рис. 47
47
Плоскость на эпюре можно задать следами (рис. 46, а и в).
Как известно, следом плоскости называют линию пересечения
плоскости с плоскостью проекций. Горизонтальный след плос-
кости h
0
α
= α I π
1
, а фронтальный след плоскости f
0
α
= α I π
2
.
Точка пересечения следов X
α
называется точкой схода следов
(рис. 46, а и в);
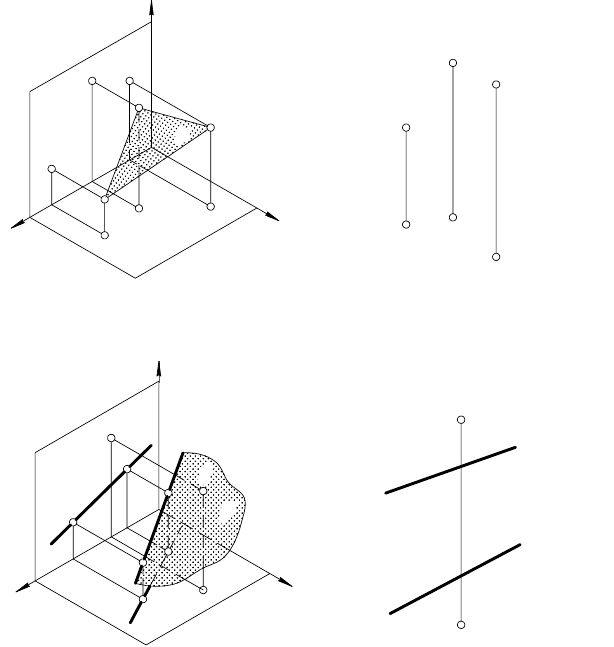
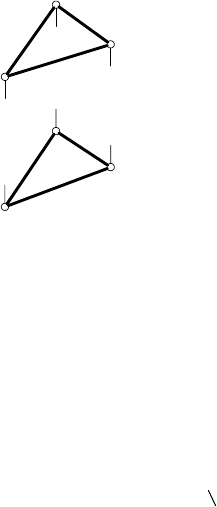
г) двух прямых, пересекающихся в несобственной точке
(рис. 47, а и б
)
()
⎩
⎨
⎧
⇔β
,
;
1111
2222
DC||BA
DC||BA
CD||AB
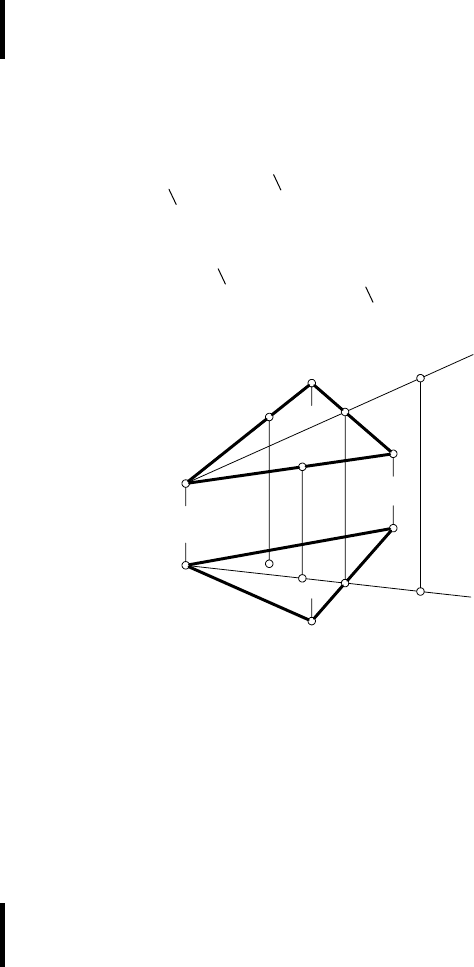
е) отсека любой плоской фигуры Ф (рис. 48).
Очевидно, что каждый из перечисленных
способов задания плоскости на эпюре допуска-
ет возможность перехода от одного из них к
другому. Например, соединив между собой точ-
ки А, В и С отрезками прямых линий
(рис. 44, а и б
) получим плоскость α, заданную
UАВС; взяв на прямой m произвольную точку
(рис. 45, а и б
) и соединив ее с точкой С, полу-
чим плоскость, заданную двумя пересекающи-
мися прямыми и т. д.
Задание плоскости на эпюре любым из
предложенных способов означает, что в этой
плоскости можно выполнять различные по-
строения: брать точки, принадлежащие плоскости, проводить
прямые, чертить различные геометрические фигуры и т. п.
(см. 3.4.).
3.4. ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ ПЛОСКОСТИ
Для точки и плоскости возможны лишь два случая их вза-
имного расположения (взаимодействия) (см. 1.3., табл. 5): точка
принадлежит (инцидентна) плоскости В
∈α или точка не при-
надлежит плоскости В ∈ α.
Условие принадлежности точки плоскости базируется на ин-
вариантном свойстве 2 ортогонального проецирования
(см. 1.5.), из которого следует:
⎩
⎨
⎧
∈
∈
⇔∈
;
;
22
11
lB
lB
lB
и
⎩
⎨
⎧
α⊂∈
α⊂∈
⇔α⊂∈
222
111
;
lB
lB
lB
или
A
1
C
1
B
1
B
2
A
2
C
2
Ô
2
Ô
1
Рис. 48
48
точка принадлежит плоскости, если она принадлежит прямой,
расположенной в этой плоскости.
На рис. 49 точка В инцидентна плоскости α, заданной
UKLM, так как лежит на прямой l, расположенной в этой плос-
кости. Точки C и D не принадлежат плоскости α (UKLM), так
как не принадлежат прямым, расположенным в плоскости α:
(
)
()
⎩
⎨
⎧
∆α⊂∈
∆α⊂∈
⇔α∈
;
;
2222222
1111111
MLKLKC
MLKLKC
C
⎩
⎨
⎧
≡∈
∈
⇔∈
,
;
1111
222
MKlD
MKD
D
α
.
K
1
M
1
L
1
L
2
K
2
M
2
C
1
D
1
1
1
B
1
l
2
B
2
l
1
1
2
C
2
a
2
a
1
D
2
Рис. 49
Для определения на эпюре взаимного расположения точки и
плоскости, в плоскости проводят прямую так, чтобы одна ее
проекция прошла через одноименную проекцию точки. Затем
сравнивают взаимное расположение второй пары одноименных
проекций точки и прямой: если проекция точки лежит на про-
екции прямой, то точка принадлежит плоскости, в противном
случае точка не
принадлежит плоскости.
Условие принадлежности прямой плоскости вытекает из из-
вестного положения стереометрии:
прямая принадлежит плоскости, если две ее точки принадлежат
этой плоскости.

49
На рис. 49 прямая l ⊂ α (UKLM), так как точки К и 1 пря-
мой l принадлежат плоскости α, заданной UKLM.
3.5. ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскость относительно плоскостей проекций π
1
, π
2
и π
3
может занимать общее и частное положение.
Плоскость общего положения наклонена к каждой из плоскостей
проекций под углом, отличным от 0 ° и 90 ° (см. рис. 44—48).
Плоскости общего положения могут быть по отношению к
наблюдателю восходящими или нисходящими.
Восходящая плоскость по мере удаления от наблюдателя повы-
шается.
Проекции такой плоскости ориентированы одинаково. На-
пример, на рис. 48 плоскость α (UАВС ) — восходящая (обход
вершин А
1
, В
1
, С
1
— по направлению часовой стрелки, и
А
2
, В
2
, С
2
— в том же направлении).
Нисходящая плоскость по мере удаления от наблюдателя пони-
жается (см. рис. 49).
Частные случаи расположения плоскости
Частное расположение относительно плоскостей проекций зани-
мают плоскости, параллельные или перпендикулярные одной из
плоскостей проекций.
Проецирующие плоскости
Плоскость, перпендикулярная одной из плоскостей проекций, на-
зывается проецирующей.
Согласно инвариантному свойству 1 а ортогонального про-
ецирования (см. 1.5.), проекции таких плоскостей на плоскости
проекций, которым они перпендикулярны, совпадают с их од-
ноименным следом (вырождаются в прямую линию).
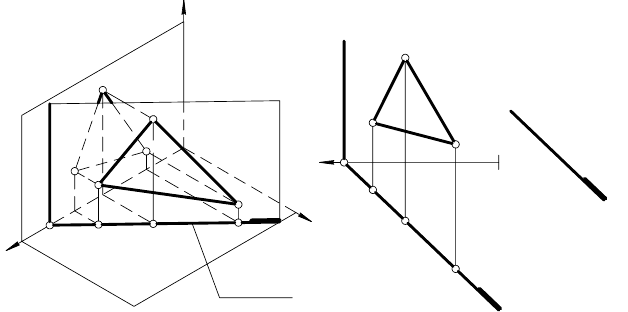
50
1. Горизонтально проецирующая плоскость α ⊥ π
1
(рис. 50 а,
б и в).
Î
p
2
x
y
z
p
1
x
X
a
X
a
f
O
a
a
C
2
B
2
A
B
C
C
1
A
2
A
1
a
1
≡
h
0
a
a
1
≡
h
0
a
A
2
B
2
C
2
C
1
A
1
B
1
B
1
a
1
≡
h
0
a
f
O
a
Î
а б в
Рис. 50
Горизонтальная проекция плоскости α ⊥ π
1
совпадает с ее
горизонтальным следом: α
1
≡ h
0
α
, а фронтальный след f
0
α
пер-
пендикулярен оси x. Горизонтальная проекция любой точки, рас-
положенная в горизонтально проецирующей плоскости, принадле-
жит ее горизонтальному следу, совпадающему с ее одноименной
проекцией: А
1
⊂ α
1
≡ h
0
α
, В
1
⊂ α
1
≡ h
0
α
, С
1
⊂ α
1
≡ h
0
α
(рис. 50, а и б
),
а фронтальная проекция каждой из этих точек лежит на верти-
кальной линии связи, проведенной через их горизонтальные
проекции. В безосной системе горизонтально проецирующую
плоскость задают ее вырожденной в прямую горизонтальной
проекцией, совпавшей с горизонтальным следом α
1
≡ h
0
α
. На
чертеже совпавшие след и проекцию определяют утолщением
(рис. 50, в).
2. Фронтально проецирующая плоскость β ⊥
π
2
(рис. 51 а, б
и в).
Фронтальная проекция любой точки, расположенной в плоско-
сти β ⊥ π
2
, принадлежит фронтальной проекции плоскости, сов-
павшей с ее фронтальным следом. Это условие является необхо-
димым и достаточным для того, чтобы точка принадлежала
фронтально проецирующей плоскости: А
2
⊂ f
0
β
≡ β
2
⇔ А ∈ β ⊥ π
2
.
Горизонтальная проекция любой точки, принадлежащей фрон-
тально проецирующей плоскости, лежит на одной вертикальной
линии связи с ее фронтальной проекцией (рис. 51, а и б
). В
безосной системе фронтально проецирующую плоскость задают

51
одной ее фронтальной проекцией (вырожденной в прямую),
совпавшей с ее фронтальным следом
β
2
≡ f
0
β
(рис. 51, в).
x
y
z
O
p
1
p
2
z
y
h
0
b
O
x
A
A
2
A
1
X
b
X
b
A
2
b
A
1
h
0
b
b
2
≡
f
0
b
b
2
≡
f
0
b
b
2
≡
f
0
b
а б в
Рис. 51
3. Профильно проецирующая плоскость γ
⊥
π
3
(рис.
52,
а, б и в).
x
y
z
p
1
p
3
A
3
z
x
y
y
A
2
g
3
≡
p
0
g
h
0
g
O
O
g
3
≡
p
0
g
g
3
≡
p
0
g
h
0
g
Y
g
Y
g
g
A
2
A
1
A
A
3
p
2
а б в
Рис. 52
Принадлежность профильной проекции любой точки плоскости
ее профильному следу является необходимым и достаточным ус-
ловием принадлежности точки профильно проецирующей плоско-
сти:
Α
3
∈p
0
γ
≡ γ
3
⇔
Α
∈
γ .
Фронтальная проекция точки лежит на одной горизонталь-
ной линии связи с ее профильной проекцией (рис. 52, б
).
