Мота А.Н. Конспект лекций по начертательной геометрии

82

екций, а значит, и фронтальная проекция А

2

точки А

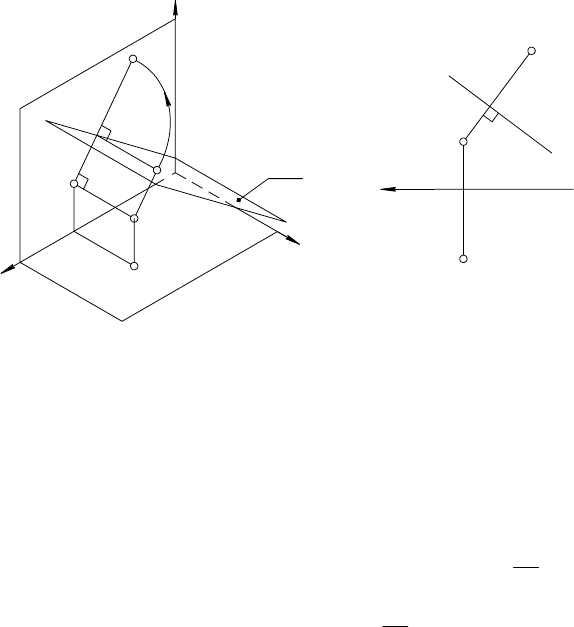
(рис. 89, а и б ). Итак, для определения новой горизонтальной

проекции выполняют следующие построения (рис. 89, б ):

1) проводят новую ось проекций х

1

;

2) через незаменяемую проекцию А

2

точки А проводят новую

линию связи ( А

2

1

x

A

) перпендикулярно оси х

1

;

3) замеряют расстояние | А

x

А

1

| от старой оси х до заменяе-

мой проекции точки А

1

и откладывают его от новой оси х

1

по

новой линии связи на поле плоскости π

3

( | А

x

А

1

| = |

1

x

A

А

3

| ).

p

2

x

y

z

p

3

A

3

A

2

A

3

p

1

A

1

A

x

1

A

X

p

1

A

X

1

2

p

3

1

A

2

A

1

x

2

p

3

x

1

p

1

A

X

1

A

3

A

X

1

а б

Рис. 89

Замена двух плоскостей проекций

Часто при решении задач замены одной плоскости проекций

бывает недостаточно. В таких случаях осуществляют замену двух

плоскостей проекций.

Рассмотрим, как определяются новые ортогональные проек-

ции точки в новой системе плоскостей проекций

3

4

2

π

x

, если

известны ее проекции в старой системе

1

2

π

x

(рис. 90).

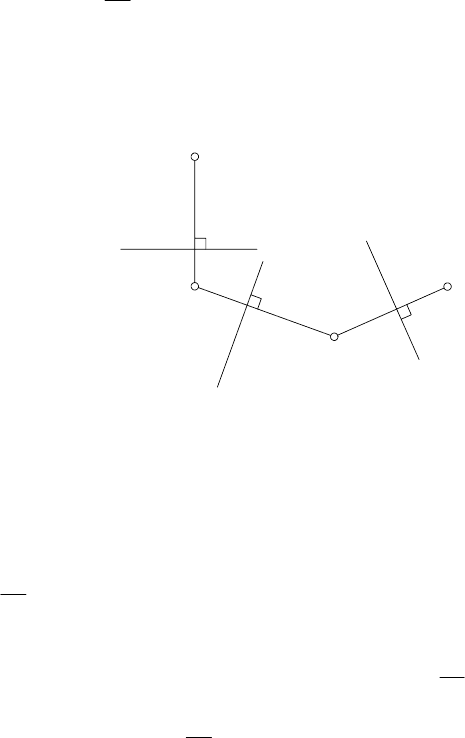
83

Для того чтобы определить новые проекции А

3

и А

4

точки А

в системе

4

3

2

π

x

заменяют сначала плоскость π

2

новой плоско-

стью π

3

. Направление новой оси выбирается, в данном случае

произвольно, так как строится новая проекция одной точки А.

Выполняя построения, следует следить за тем, чтобы не

происходило наложения новых проекций на старые.

A

X

2

A

2

p

2

p

1

x

2

s

x

1

p

1

p

3

x

2

p

4

p

3

A

3

A

4

A

1

A

X

1

A

X

Рис. 90

Для определения новой фронтальной проекции А

3

нужно

провести новую линию связи перпендикулярно к новой оси х

1

и

отложить на ней от точки

1

x

A

отрезок равный | А

x

А

2

|.

Положение новой горизонтальной проекции А

4

в системе

4

3

2

π

x

определяется аналогично ранее рассмотренному случаю

замены горизонтальной плоскости проекций. Отличие состоит

лишь в том, что за исходную берут систему

1

3

1

π

x

и от нее пе-

реходят к системе

4

3

2

π

x

. В этом случае плоскость π

3

не меняет

своего положения в пространстве, следовательно проекция А

3

остается неизменной. Новая горизонтальная проекция А

4

опре-

делится, если из точки А

3

провести линию связи перпендику-

лярно х

2

(в данном случае выбирается произвольно) и отложить

на ней от точки

2

x

A

отрезок [

2

x

A

А

4

] равный расстоянию

|

1

x

A

А

1

|. Очевидно, что во всех рассматриваемых случаях замены

84

плоскостей проекций, проекции точки строятся в одном и том

же порядке.

Приведенные рассуждения позволяют определить алгоритм

построения новой проекции точки:

1. Провести новую ось проекций согласно поставленным условиям.

2. Через незаменяемую проекцию точки провести новую линию

связи перпендикулярно новой оси.

3. Замерить расстояние от старой оси до заменяемой проекции

точки и отложить его от новой оси по новой линии связи на но-

вом поле плоскости проекций.

Этот алгоритм применим для построения новой проекции

точки при выполнении одной, двух, трех и т. д. последователь-

ных замен плоскостей проекций.

Рассмотренный в 2.2. алгоритм построения третьей проек-

ции точки является частным случаем представленного алгорит-

ма.

Зная правила построения проекции одной точки в новой

системе плоскостей проекций, можно построить новые проек-

ции

любого числа точек, а следовательно, и любой геометриче-

ской фигуры.

Новая ось проекций при решении задачи определяется в за-

висимости от ее условия (параллельно или перпендикулярно

прямой или плоскости).

ЗАДАЧА 1. Прямую общего положения ( АВ ) перевести

в положение фронтали (рис. 91).

РЕШЕНИЕ.

1.

1

2

π

x

→

1

3

1

π

x

, π

3

|| AB ⇒ x

1

|| A

1

B

1

;

2.

AB (A

1

B

1

, А

3

В

3

) || π

3

, где π

3

новая

фронтальная плоскость проекций.

Новые проекции А

3

и В

3

точек А и В

строят по алгоритму:

Построения для точки А

3

.

а) х

1

|| А

1

В

1

;

б) ( А

1

x

A

) ⊥ х

1

∧ ( А

1

x

A

) I х

1

=

1

x

A

;

в) |

1

x

A

А

3

| = | А

2

А

x

|;

A

2

p

2

p

1

x

1

p

1

p

3

B

3

B

2

B

1

2

1

2

A

3

A

1

A

X

1

B

X

1

B

X

A

X

Рис. 91

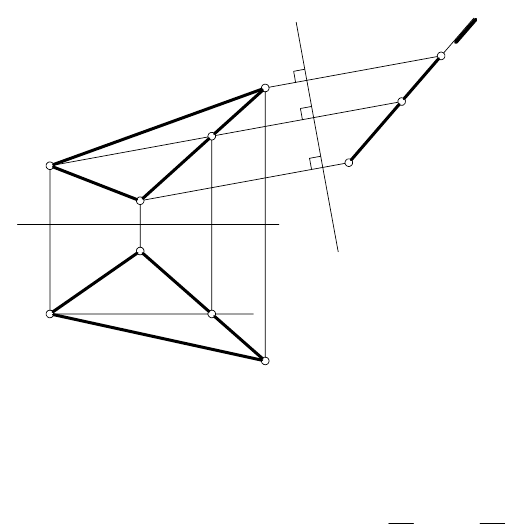
85

Построения для точки В

3

.

а) х

1

|| А

1

В

1

(проведена);

б) ( В

1

x

B

) ⊥ х

1

∧ ( В

1

x

B

) I х

1

=

1

x

B

;

в) |

1

x

B

В

3

| = | В

2

В

x

|.

ЗАДАЧА 2. Плоскость α (

U

ABC ) перевести в положение

горизонтально проецирующей (рис. 92).

x

1

A

3

≡

f

3

≡

1

3

C

1

B

1

f

1

2

1

2

A

2

C

2

B

2

A

1

p

2

p

1

f

2

B

3

C

3

s

x

1

p

3

p

2

a

3

2

1

s

1

2

Рис. 92

РЕШЕНИЕ.

Горизонтально проецирующая плоскость перпендикулярна

плоскости проекций π

1

. Поэтому заменить следует плоскость

проекций π

1

, т. е. осуществить переход

1

2

π

x

→

3

2

1

π

x

, где

π

3

⊥ α (

U

ABC ). Согласно признаку перпендикулярности двух

плоскостей (см. 4.6.), плоскость α (

U

ABC ) должна содержать

прямую, перпендикулярную плоскости π

3

. Так как плоскость

π

3

⊥ π

2

, то эта прямая — фронталь f ⊂ α (

U

ABC ):

α (

U

ABC ) ⊃ f || π

2

⊥ π

3

⇒ α (

U

ABC )

⊥

π

3

.

Порядок построений:

1.

f ⊂ α (

U

ABC );

86

2.

1

2

π

x

→

3

2

1

π

x

; π

3

⊥ f ⇒ х

1

⊥

f

2

.

3.

Точки А

3

, В

3

и С

3

строят по алгоритму, А

3

В

3

С

3

≡ α

3

. Плос-

кость α (

U

ABC ) на π

3

, которой она перпендикулярна,

проецируется в прямую линию (см. 3.5.).

6.3. СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ

Название способа плоскопараллельного перемещения опре-

деляет путь изменения взаимного положения проецируемой фи-

гуры и плоскостей проекций. Этот путь осуществляется пере-

мещением геометрической фигуры в новое положение так, что

ее точки двигаются во взаимно параллельных плоскостях, при

этом плоскости проекций не меняют своего положения в про-

странстве.

В зависимости от расположения параллельных

плоскостей,

по отношению к плоскостям проекций, и вида траектории дви-

жения точек различают несколько способов плоскопараллельно-

го перемещения.

1. Способ параллельного перемещения. Плоскости, в кото-

рых перемещаются точки, параллельны одной из плоскостей

проекций. Траектории точек — произвольные плоские линии.

Частный случай способа параллельного перемещения — спо-

соб вращения вокруг проецирующей прямой. При этом

способе

плоскости перемещения точек параллельны одной из плоско-

стей проекций. Траектории точек — дуги окружностей с центра-

ми, расположенными на оси вращения.

2. Вращение вокруг оси, параллельной одной из плоскостей

проекций (вращение вокруг линии уровня). Плоскости переме-

щения точек перпендикулярны оси вращения. Траектории то-

чек — дуги окружностей с центром на оси вращения

. Частным

случаем этого способа является способ вращения вокруг следа

плоскости (способ совмещения). Плоскости перемещения точек

перпендикулярны следу плоскости. Траектории точек — дуги

окружностей с центрами на следе плоскости (оси вращения).

Рассмотрим каждый из этих способов.

87

Способ параллельного перемещения (переноса)

Для параллельного перемещения справедлива следующая

теорема:

при параллельном переносе

геометрической фигуры отно-

сительно плоскости проекций,

проекция фигуры на эту плос-

кость хотя и меняет свое по-

ложение, но остается конгру-

энтной проекции фигуры в ее

исходном положении.

Если фигура Ф плоская и

перемещается в плоскости α,

параллельной плоскости про-

екций π

1

(рис. 93), то, на ос-

новании свойства 2 б

(см. 1.5.), имеем:

Ф ≅ Ф

1

∧ Ф

1

≅

1

Ф

.

Фигура Ф ≅ Ф

1

по определению конгруэнтных фигур

(см. 1.5., табл. 2), следовательно, Ф

1

≅

1

Ф

.

Теорема верна и в том случае, когда фигура Ф занимает об-

щее положение относительно плоскости проекций.

Свойства параллельного перемещения

1. При всяком перемещении точки в плоскости, параллельной

плоскости проекций π

1

, ее фронтальная проекция перемещается

по прямой, параллельной оси х.

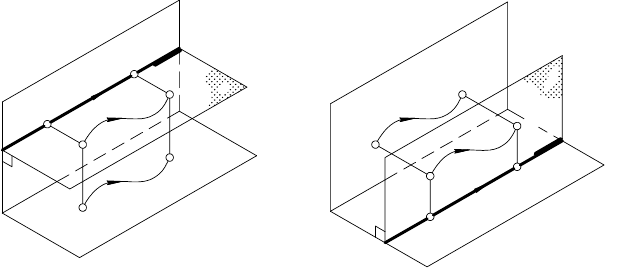
На рис. 94 плоскость α || π

1

. В этой плоскости перемещается

точка А по произвольной траектории l в точку А

1

. На основании

свойства 2 а (см. 1.5.) имеем:

( l ⊂ α ) ∧ ( α ⊥ π

2

) ⇒ l

2

⊂ f

0

α

≡ α

2

.

Фронтальный след f

0

α

плоскости α параллелен оси х, так как

α ||π

1

⊥ π

2

, и α I π

2

= f

0

α

|| х

, следовательно, f

0

α

≡ l

2

|| х.

2. Если точка перемещается по произвольной траектории в

плоскости, параллельной плоскости π

2

, то ее горизонтальная

проекция перемещается по прямой, параллельной оси х .

Рис. 93

p

1

Î

p

2

a

A

1

A

1

a

2

B

1

2

h

C

1

B

1

B

1

C

1

C

1

B

1

A

1

h

1

Ô

1

Ô

1

Ô

1

B

2

x

88

p

1

Î

p

2

a

A

2

A

1

A

1

A

1

a

2

= f

0

a

A

1

2

l

2

l

1

p

1

B

1

m

1

B

1

b

Î

B

1

2

m

2

B

2

p

2

m

B

1

b

1

= h

0

b

x

Рис. 94 Рис. 95

Точка В перемещается в плоскости β || π

2

(рис. 95) по линии

m в точку В

1

. Траектория движения точки m ⊂ β ⊥ π

1

. Из свой-

ства 2 а (1.5.) следует: ( m ⊂ β ) ∧ ( β ⊥ π

1

) ⇒ m

1

≡ h

0

β

≡ β

1

. Но

взаимно параллельные плоскости β и π

2

пересекаются плоско-

стью π

1

по параллельным прямым х и h

0

β

≡ β

1

, значит,

h

0

β

≡ m

1

|| х.

Применяя теорему и свойства параллельного проецирова-

ния, определяют положение новых, удобно расположенных про-

екций геометрической фигуры по заданным ортогональным

проекциям. Т. е. заданные геометрические фигуры, занимающие

произвольное положение относительно плоскостей проекций,

переводят в частное (параллельное или перпендикулярное) по-

ложение относительно той же системы плоскостей проекций.

Рассмотрим примеры.

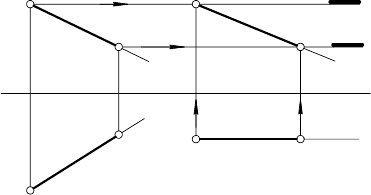
ЗАДАЧА 1. Отрезок

прямой [СD ] перевести в положе-

ние, параллельное π

2

(рис. 96).

РЕШЕНИЕ.

Отрезок [CD

] нужно перевести в положение параллельное π

2

(в положение фронтали). Горизонтальная проекция любой

фронтали параллельна оси х, т. е. расположена горизонтально.

Переведем отрезок [C

1

D

1

] в горизонтальное положение. Пере-

мещение отрезка в новое положение осуществляется так, что

его точки двигаются в плоскостях, параллельных π

1

. При таком

перемещении новая горизонтальная проекция [

1

DC

] отрезка

[CD] конгруэнтна исходной (на основании теоремы):

[

1

DC

] ≅ [C

1

D

1

].

89

D

1

2

C

1

2

D

1

C

1

x

f

0

a

m

1

2

C

2

D

2

D

1

C

1

m

2

m

1

f

0

b

m

1

2

Рис. 96

Фронтальные проекции C

2

и D

2

точек отрезка [CD ] переме-

щаются в новое положение по прямым f

0

α

и f

0

β

, параллельным

оси х (свойство 1).

Порядок построения:

1)

1

C

выбирают произвольно;

2)

1

C

⊂

1

m

|| х;

3)

[

1

DC

] ≅ [C

1

D

1

];

4)

С

2

⊂ f

0

α

|| х;

5)

D

2

⊂ f

0

β

|| х;

6)

[

1

2

1

CC

) ⊥ х ∧

1

2

1

CC

I f

0

α

=

1

2

C

;

7)

[

1

2

1

DD

) ⊥ х ∧

1

2

1

DD

I f

0

β

=

1

2

D

;

8)

1

2

C

U

1

2

D

= [

1

2

1

2

DC

];

9)

[С

1

D

1

] ([

1

DC

], [

1

2

1

2

DC

]) || π

2

, так как [

1

DC

] || х.

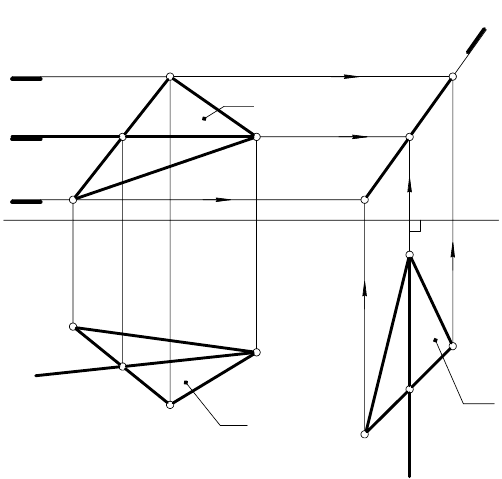
ЗАДАЧА 2. Плоскость общего положения α (

U

ABC ) пе-

ревести в положение фронтально проецирующей (рис. 97).

РЕШЕНИЕ.

Плоскость α (

U

ABC ) должна занять положение фронтально

проецирующей, т. е. перпендикулярной плоскости проекций π

2

.

Чтобы осуществить перемещение плоскости α в новое положе-

ние, проводят горизонталь h ⊂ α (

U

ABC ). В новом положении

горизонталь h должна стать перпендикулярной плоскости π

2

и

спроецироваться на фронтальную плоскость проекций в точку

1

2

1

2

1

2

C1h ≡≡

. Поэтому ее новая горизонтальная проекция

1

h

должна быть расположена перпендикулярно оси х. Перемеще-

ние плоскости α (

U

ABC ) в новое положение должно осуществ-

90

ляться так, чтобы все ее точки двигались в плоскостях, парал-

лельных плоскости π

1

. При таком перемещении новая горизон-

тальная проекция

U

ABC (а значит, и отрезка [

С

1

]

горизонтали h) конгруэнтна исходной:

U

А

1

В

1

С

1

≅

U

1

CBA

(на

основании теоремы).

f

0

d

h

2

1

2

A

2

C

2

B

2

1

A

1

C

1

B

1

x

f

0

b

f

0

g

a

1

2

B

1

2

h

1

h

1

C

1

B

1

A

1

a

2

a

1

a

1

h

1

2

≡

1

2

≡

C

1

2

4

3

5

2

4

5

3

2

A

1

2

1

Рис. 97

Фронтальные проекции точек будут перемещаться по пря-

мым f

0

β

, f

0

γ

, f

0

δ

, параллельным оси х (см. свойство 1).

Порядок построений:

1.

Через произвольную точку

1

C

провести прямую

1

h

⊥ х;

2.

Отложить на этой прямой отрезок [

1

1C

] ≅ [

С

1

];

3.

Построить

U

1

CBA

≅

U

А

1

В

1

С

1

;

4.

A

2

∈ f

0

δ

|| х ∧ (

1

2

1

AA

) ⊥ х ; (

1

2

1

AA

) I f

0

δ

=

1

2

A

;

5.

B

2

∈ f

0

γ

|| х ∧ (

1

2

1

BB

) ⊥ х ; (

1

2

1

BB

) I f

0

γ

=

1

2

B

;

6.

C

2

∈ f

0

β

|| х ∧ (

1

2

1

CC

) ⊥ х ; (

1

2

1

CC

) I f

0

β

=

1

2

C

;

7.

1

2

A

U

1

2

C

U

1

2

B

=

1

2

A

1

2

B

1

2

C

≡

1

2

α

.

91

Лекция 7 (2 часа)

Тема «Способы преобразования ортогональных

проекций»

План

1.

Способ вращения вокруг оси, перпендикулярной плоскости

проекций.

2.

Способ вращения вокруг оси, параллельной плоскости про-

екций.

7.1. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ОСИ, ПЕРПЕНДИКУЛЯРНОЙ

К ПЛОСКОСТИ ПРОЕКЦИЙ

Вращение вокруг оси перпендикулярной к плоскости проек-

ций, т. е. проецирующей оси, является частным случаем парал-

лельного перемещения (см. 6.3.). Отличие состоит лишь в фор-

ме траектории движения точки. При параллельном перемеще-

нии траектория точки — произвольная линия, а при вращении

вокруг проецирующей оси — окружность. Центр окружности

расположен на оси вращения, а ее

радиус r равен расстоянию от

вращающейся точки до оси.

При вращении вокруг горизонтально проецирующей оси i

(рис. 98, а и б ) точка А перемещается в плоскости

α (α ⊥ i ⇒ α || π

1

) по дуге окружности, которая на плоскость π

1

проецируется без искажения, а на плоскость π

2

— в отрезок

прямой, перпендикулярной проекции оси вращения.

Из сказанного выше следует:

при вращении точки вокруг горизонтально проецирующей оси ее

горизонтальная проекция перемещается по окружности с цен-

тром в точке, являющейся горизонтальной проекцией оси враще-

ния, радиусом равным расстоянию между горизонтальными про-

екциями оси и точки; а фронтальная проекция — по прямой, пер-

пендикулярной фронтальной проекции оси вращения.

Вращение точки вокруг оси i ⊥ π

2

показано на рис. 99, а и б.

Точка перемещается в новое положение А

1

по окружности, рас-

положенной в плоскости β ⊥ i . Так как i ⊥ π

2

, то β || π

2

.

Мота А.Н. Конспект лекций по начертательной геометрии

Подождите немного. Документ загружается.