Натареев С.В. Моделирование и расчет процессов химической технологии
Подождите немного. Документ загружается.


80
L
G
Г
θ
=
θ
. (3.5.3)
Граничные условия (по Данквертсу):
H
x
G
G
Нх
GвхG
dx
d
Dvv
=
=
θ
+θ=θ ; (3.5.4)
0
dx
d
0x
G
=
θ
=
; (3.5.5)
0x
L
L
0х
LвхL
dx
d
Dww
=
=
θ
−θ=θ ; (3.5.6)
0
dx
d
H
x
L
=
θ
=
. (35.7)
Здесь
G
θ
и
L
θ
- концентрация целевого компонента в газе и жидкости,
pG
θ
- равновесная концентрация целевого компонента в газе, v и w – скорость
потока газа и жидкости, K
G
– коэффициент массопередачи, Г – постоянная
Генри, х – продольная координата, Н – высота насадки, индексы: вх –
входящий, вых – выходящий.
Для нахождения функций )x(
G
θ
и )x(
L
θ
достаточно решить одно
уравнение (3.5.2). Функцию )x(
G
θ
, после того как найдена функция )x(
L
θ
,
можно найти из уравнения материального баланса:
)(L)(G
LвыхLGвхG
θ
−
θ
=
θ
−
θ
, (3.5.8)
где G и L – массовые расходы газа и жидкости.
Используем в уравнении материального баланса (3.5.2) уравнение
равновесия (3.5.3) и введем следующие переменные:
LвхL
N
θ
−
θ
=
;
L
D
wH
Pe = ;
L
G
D
HГK
E =
;
H
x
z = . (3.5.9)
Уравнение материального баланса по жидкой фазе и соответствующие
граничные условия примут вид:
0EN
dz
dN
Pe
dz
Nd
2
2
=−− ; (3.5.10)
81
0
z
0z
вх
dz
dN
Pe
1
NN
=
=
−= ; (3.5.11)
0
dz
dN
1
z
=
=
. (3.5.12)
Общее решение дифференциального уравнения (3.5.10) имеет вид:
zr
2
zr
1
21
eAeAN += , (3.5.13)
где r
1
, r
2
– корни характеристического уравнения:
0ErPer
2
=−− , (3.5.14)
т.е.
E
2
Pe
2
Pe
r
2
2,1
+
±= . (3.5.15)
Константы А
1
и А
2
найдем, используя граничные условия.
Подстановка z=0 и N=1 в (3.5.11) дает:
( )
вх221121
NArAr
Pe
1
AA =+−+ . (3.5.16)
Удовлетворим решение (3.5.10) условию (3.5.12):
0eAreAr
21
r
2
2
r
1
1
=+ . (3.5.17)
Решая совместно уравнения (3.5.16) и (3.5.17), находим:
−+−
−=
2
r
r
2
r
1
r
2
r
1
r
2вх
1
r
Ре
1
e
er
Ре
1
er
er
1er
erN
A
1
2
1
2
1
2
; (3.5.18)
2
r
r
2
r
1
r
2
вх
2
r
Ре
1
e
er
Ре
1
er
er
1
N
A
1
2
1
2
−+−
= . (3.5.19)
Подставим значения А
1
и А
2
в уравнение (3.5.13) и запишем решение
задачи в прежних переменных:

82
2
r
r
2
r
1
r
2
Н
х
rrr
1
2
Н
х
r
вхLmaxL
LmaxL
r
Ре
1
e
er
Ре
1
er
er
1
e
r
г
e
1
2
1
2
1122
−+−
−
=
θ−θ
θ−θ
+−
. (3.5.20)
На рис. 3.8 представлен пример расчета кривых изменения концентрации
целевого компонента в жидкой и газовой фазах по высоте насадочного
абсорбера, выполненный в системе Mathcad.
Рис. 3.8. Пример расчета насадочного абсорбера
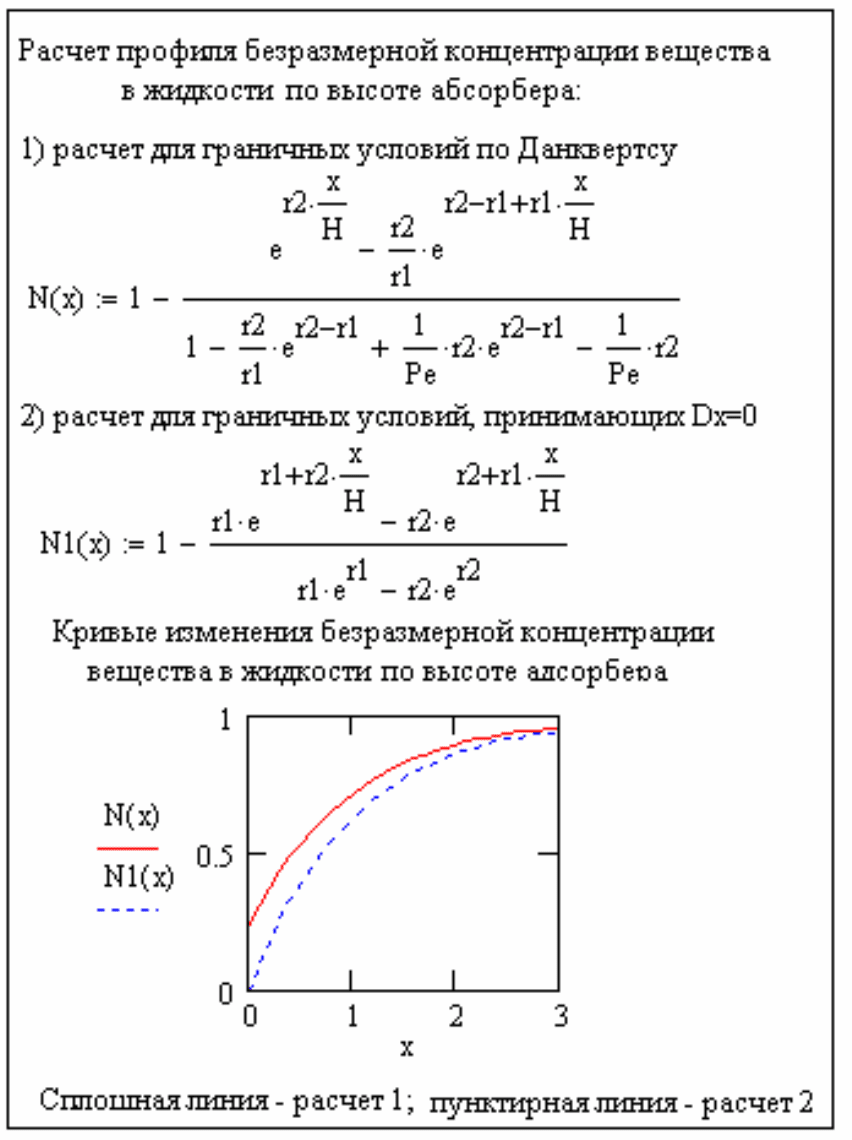
83
Окончание рисунка 3.8
Из приведенных на рис. 3.8 кривых видно, что концентрация целевого
компонента в жидкости на входе в абсорбер в случае расчета при граничных
условиях по Данквертсу уменьшается скачкообразно по причине влияния
продольного перемешивания.
84
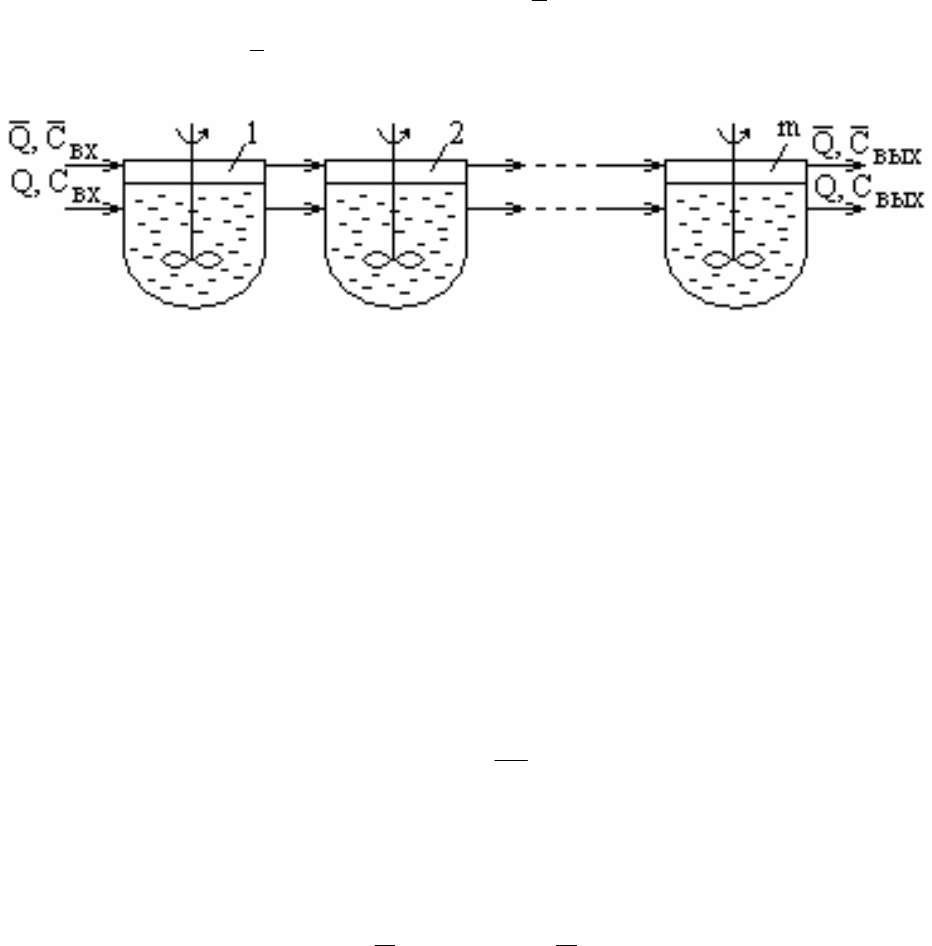
3.5. Каскад адсорберов емкостного типа с мешалками
В каскаде емкостных аппаратов одинакового объема протекает
непрерывный прямоточный процесс очистки раствора с помощью адсорбента
(рис. 3.9). Общее количество аппаратов в каскаде равно m. В первый аппарат
каскада поступают раствор с объемной скоростью Q и концентрацией С
вх
, а
также адсорбент с объемной скоростью Q и с начальным содержанием
целевого компонента
вх
C .
Рис. 3.9. Схема движения фаз в каскаде реакторов
При постановке математической модели сделаем следующие допущения:
равновесие в системе адсорбент-раствор описывается уравнением линейной
изотермы адсорбции, скорость процесса определяется смешенной диффузией,
перемешивание жидкой и твердой фаз является идеальным, частицы адсорбента
имеют сферическую форму со средним диаметром 2r
0
.
Введем в рассмотрение безразмерное время:
0
τ
τ
=θ
. (3.6.1)
С учетом формулы (3.6.1) запишем уравнение для расчета средней
концентрации целевого компонента в адсорбенте на выходе из i-го аппарата:
() ()
θθ
∫
θ=
∞
dCfC
icp
0
iвых
. (3.6.2)
Для описания структуры потоков используем ячеечную модель. Функция
распределения времени пребывания частиц адсорбента имеет вид:

85
()
( )
( )
θ−θ
−
=θ
−
mexp
!1m
m
f
1m
m
, (3.6.3)
где m − число ячеек.
В качестве уравнения кинетики используем решение задачи о поглощении
целевого компонента частицей сферической формы при граничных условиях
первого рода [2], которое запишем с учетом введения безразмерного времени
(3.6.1):
∑
∞
=
θ
τµ
−−=
−
−θ
1n
2
0
i0эф
2
n
n
iвх0
iвхicp
r
D
expA1
Ca
C)(C
, (3.6.4)
где
2
n
n
6
A
µ
= ,
π
=
µ
n
n
, а
0
– предельное значение адсорбции,
эф
D –
коэффициент диффузии в адсорбенте, r
0
– радиус частицы..
Подставляя (3.6.3) и (3.6.4) в уравнение (3.6.2) и применяя формулу
(
)
k
0
zp1k
p
!1k
dzez
−
=
∫
∞
−−
, (3.6.5)
получаем
∑
+
τµ
−=
−
−
∞
=1n
m
2
0
icpэф
2
n
m
n
iвх0
iвхiвых
m
r
D
mA
1
Ca
CC
. (3.6.6)
Уравнение (3.6.6) позволяет рассчитать степень отработки зерна
адсорбента на выходе из i–го аппарата каскада.
Замыкает математическое описание процесса уравнение материального
баланса:
(
)
(
)
iвхiвыхiвыхiвх
СCQСCQ −=−
. (3.6.7)
На рис. 3.10 приведен пример расчета каскада емкостных аппаратов,
выполненный в системе Мathcad.

86
Рис. 3.10. Пример расчета каскада адсорберов
87
3.6. Адсорбер с неподвижным слоем адсорбента
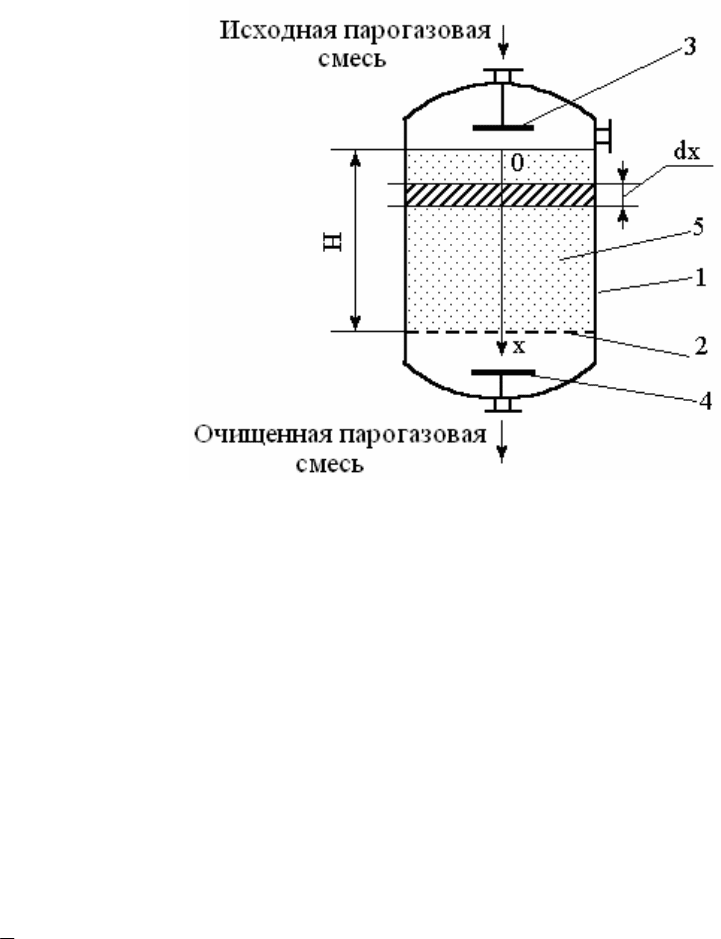
Рассмотрим процесс адсорбции целевого компонента из парогазовой
смеси в аппарате с неподвижным слоем адсорбента (рис. 3.11).
Рис. 3.11. Адсорбер с неподвижным слоем адсорбента:
1 – корпус, 2 – опорная решетка, 3 и 4 – верхнее и нижнее
распределительные устройства, 5 - слой адсорбента
Предполагаем, что слой адсорбента высотой Н является
монодисперсным. Он состоит из зерен сферической формы с диаметром 2r
0
,
имеющих однородную изотропную структуру. В момент времени, принятый
за начальный, распределение концентрации целевого компонента в твердой
(
0
C )и газовой (С
0
) фазах по высоте аппарата является равномерным. Во время
работы аппарата парогазовая смесь с объемной скоростью Q и исходной
концентрацией С
вх
поступает через верхнее распределительное устройство,
равномерно распределяется по поперечному сечению аппарата и проходит
сквозь слой адсорбента. Допустим, что движение парогазовой смеси в
88
аппарате является одномерным и зависит от координаты x. Изменение
концентрации целевого компонента в парогазовой смеси происходит за счет
его движения с некоторой средней по сечению аппарата скоростью v,
продольного перемешивания сплошной фазы и процесса адсорбции между
адсорбентом и парогазовой смесью. Очищенная парогазовая смесь выводится
из аппарата через нижнее распределительное устройство. Скорость процесса
адсорбции лимитируется внутренней диффузией. Равновесие процесса
описывается уравнением линейной изотермы Генри.
С учетом принятых допущений составим математическое описание
процесса. Математическая модель включает следующие уравнения:
уравнение материального баланса:
2
2
x
ср
x
C
D
x
C
v
C
C
∂
∂
=
∂
∂
+
τ∂
∂
+
τ∂
∂
;
(3.6.1)
- уравнение кинетики диффузии в сферическую частицу:
∂
∂
+
∂
∂
=
τ∂
∂
r
C
r
2
r
С
D
C
2
2
эф
;
(3.6.2)
начальные и граничные условия:
0
0
C),x(C
=
τ
=τ
;
(3.6.3)
вх
0
x
C),x(C =τ
=
(3.6.4)
0
x
),x(C
H
x
=
∂
τ
∂
=
;
(3.6.5)
0
0
C)r,(C =τ
=τ
;
(3.6.6)
ГС)r,(C
0
rr
=τ
=
;
(3.6.7)
0
r
)x,(C
0r
=
∂
τ∂
=
.
(3.6.8)
89
- уравнение связи между локальной концентрацией вещества в частице
)x,r,(C τ и средним ее значением )x,(C
ср
τ :
∫
τ=τ
0
r
0
2
3
0
ср
dr)x,r,(Cr
r
3
)x,(C
.
(3.6.9)
Здесь С – концентрация целевого компонента в парогазовой смеси; C -
концентрация целевого компонента в адсорбенте; D
x
– коэффициент
продольной диффузии, r – радиальная координата внутри зерна адсорбента; х
текущая координата по высоте слоя адсорбента; τ – время. Индексы: ср –
средний; о – начальный.
Концентрации С и
cp
C рассчитаны на единицу объема слоя и связаны с
традиционными концентрациями, отмеченными штрихом, соотношениями:
'
C
C
ε
=
;
'
cpcp
C)1(C ε−= . Здесь ε – порозность слоя.
Второе слагаемое левой части уравнения (3.6.1) представляет собой сток
вещества из парогазовой фазы в твердую фазу за счет физической адсорбции.
Величина этого стока может быть найдена путем решения системы
уравнений (3.6.2), (3.6.6) – (3.6.9) по аналогии с известной задачей о переносе
теплоты в сферической частице [2]. Опуская громоздкий вывод, запишем
решение искомой задачи в новых переменных:
τπ
−
∑
π
=
−
−
∞
=
2
0
эф
22
1n
n
22
00
cp0
r
Dn
expВ
n
6
Ca
Ca
.
(3.6.10)
Здесь а
0
– предельное значение адсорбции.
Заменим второе слагаемое в левой части уравнения (3.6.1) с учетом
(3.6.10) следующим образом:
