Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.


<∆−
>∆
=
∆
∆
→∆
0 åñëè ,1
0 åñëè ,1
lim
0
x
x
x
y
x
и правая производная функции в точке x=0 отлична от
левой.
В остальных точках производная функции y=
x существует и равна
5.4. Правила вычисления производных, связанные с арифметическими
действиями над функциями
Теорема. Пусть функции y
1
=f
1
(x) и y
2
=f
2
(x) имеют производные в точке x
0
. Тогда
их сумма, разность, произведение и частное (частное при условии y
2
≠0 в точке
x=x
0
) также имеют производные в точке x=x
0
, причем
()
()
..3
..2
..1
2
2
2121
2
1
212121
2121
y
yyyy
y
y
yyyyyy
yyyy
′
−
′
=
′
′
+
′
=
′
⋅
′
±
′
=
′
±
5.5. Вычисления производных некоторых элементарных функций
1. y=c (c= const)
∆y=c-c⇒ 0lim
0
=
∆
∆
→∆
x
y
x
. Итак, 0
=
′
c .
Замечание 1. Производная произведения функции на постоянную равна
произведению этой постоянной на производную функции, т.е.
(
. yccy
′
=
′
)
Доказательство.
ycycyycyccy
′
=
′
+
⋅
=
′
+
′
=
′
0)( .
Замечание 2. Если n - любое фиксированное целое число, то
.
()
nnnn
ycycycycycyc
′
++
′
+
′
=
′
+++ ......
22112211
Следует из предыдущей теоремы с помощью метода математической индукции.
2. y=x
n
(степенная функция), где n - положительное целое число.
Если использовать формулу бинома Ньютона, получим
()
....
!2
)1(
...
!2
)1(
221
221
nnn
nnnnn
n
xxx
nn
xnx
xxxx
nn
xnxxxxy
∆++∆
−
+∆=
=−∆++∆
−
+∆+=∆+=∆
−−
−−
При ∆x≠0
....
!2
)1(
121 −−−
∆++∆
−
+=
∆
∆
nnn
xxx
nn
nx
x
y
При
∆x→0 все слагаемые правой части, начиная со второго, стремятся к нулю, т.к.
содержат
∆x в некоторой положительной степени. Первое слагаемое ∆x не
содержит, поэтому предел правой части при
∆x→0 равен nx
n-1
. Следовательно,
существует предел левой части при
∆x→0, равный nx
n-1
. По определению
производной указанный предел равен производной функции y=x
n
, т.е.
.
()
1−
=
′
=
′
nn
nxxy
Данные рассуждения справедливы для любой точки x
∈(-∞, +∞).
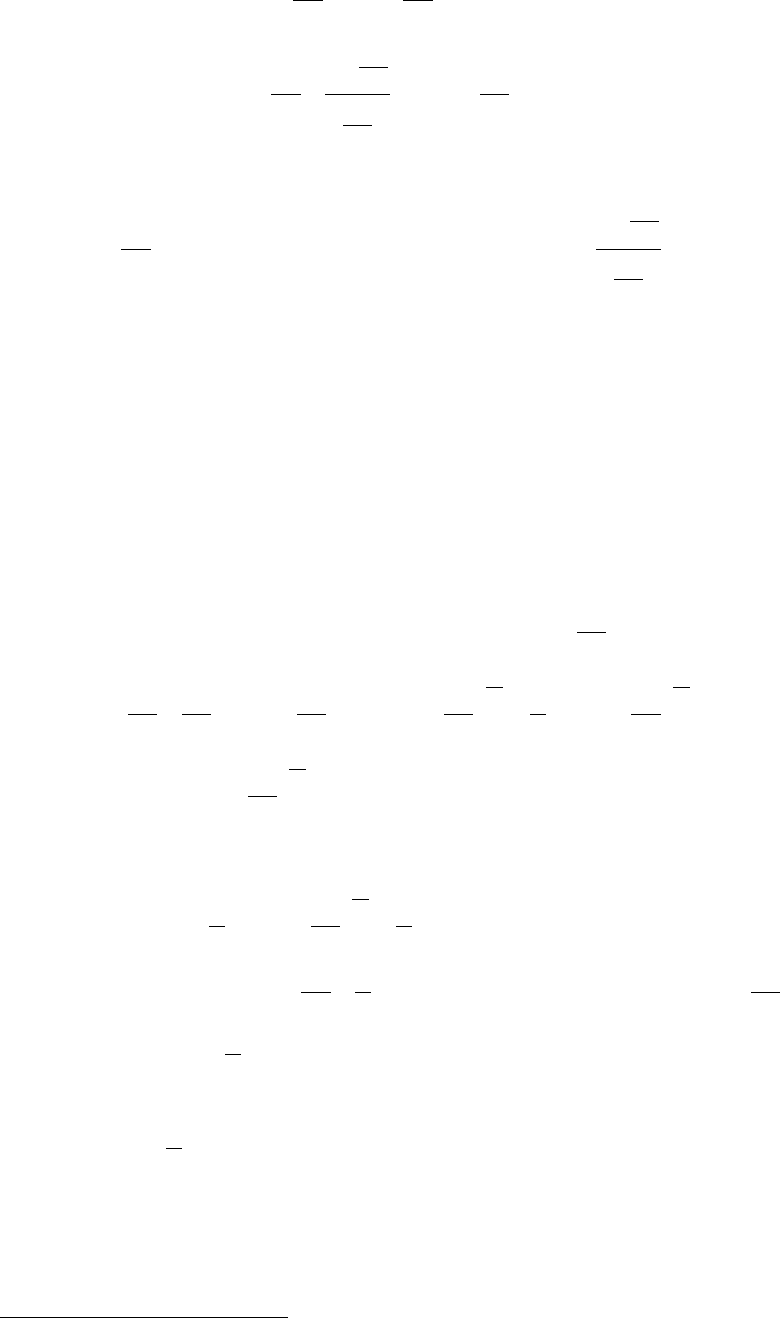
Кроме того, эту формулу можно обобщить на тот случай, когда n является
произвольным вещественным числом (доказательство этого положения см. в п.
4.6.).
3. y=sinx.
∆
+
∆
=−∆+=∆
2
cos
2
sin2sin)sin(
x
x
x
xxxy
. При ∆x≠0
∆
+⋅
∆
∆
=
∆
∆
2
cos
2
2
sin
x
x
x
x
x
y
. (1)
В силу непрерывности функции cosx в любой точке x
∈(-∞, +∞)
x
x
x
x
cos
2
coslim
0
=
∆
+
→∆
1 . Если учесть также, что 1
2
2
sin
lim
0
=
∆
∆
→∆
x
x
x
(см. п.3.16), получим,
что предел правой части равенства (1) существует и равен cosx (на основании
теоремы 1 п.3.10), а тогда и предел левой части этого равенства существует и
равен cosx. По определению производной указанный предел равен производной
функции y=sinx, т.е.
.
()
xx cossin =
′
4. Аналогичным образом можно показать, что
()
x–osx sin−=
′
.
5.
Пусть x∈(0,∞), и ∆x - произвольное приращение аргумента,
такое что
∆x <x.
(
.10log ≠<= axy
a
)
()
.1logloglog
∆
+=−∆+=∆
x
x
xxxy
aaa
При
∆x≠0 .1log
1
1log1log
1
1
x
x
a
x
aa
x
x
xx
x
x
x
xx
y
∆∆
∆
+=
∆
+=
∆
+
∆
=
∆
∆
Если x - фиксировано,
то при
e
x
x
x
x
x
=
∆
+→
∆
→∆
1lim 0
0
x
∆
и на основании непрерывности функции в
любой точке полупрямой (0,
∞) и, в частности, в точке
x
a
log
(
)
e
a
x
a
ex
logloglim =ex
=
→
получим, что
.log
1
1log
1
lim
0
e
xx
x
x
a
x
x
a
x
=
∆
+
∆
→∆
Поэтому существует предел правой части
равенства при
.log
1
lim 0
0
e
xx
y
x
a
x
=
∆
∆
→∆
→∆
Но по определению,
()
′
x
a
=
∆
∆
→∆
x
y
x
loglim
0
,
поэтому
()
.log
1
log e
x
x
aa
=
′
В частности, при а=е
имеем
()
.
1
ln
x
x
=
′
1 См., например: Ильин В.А., Позняк Э.Г. Основы математического анализа.-
-М.: Наука, 1971 (и последующие издания), ч.1.
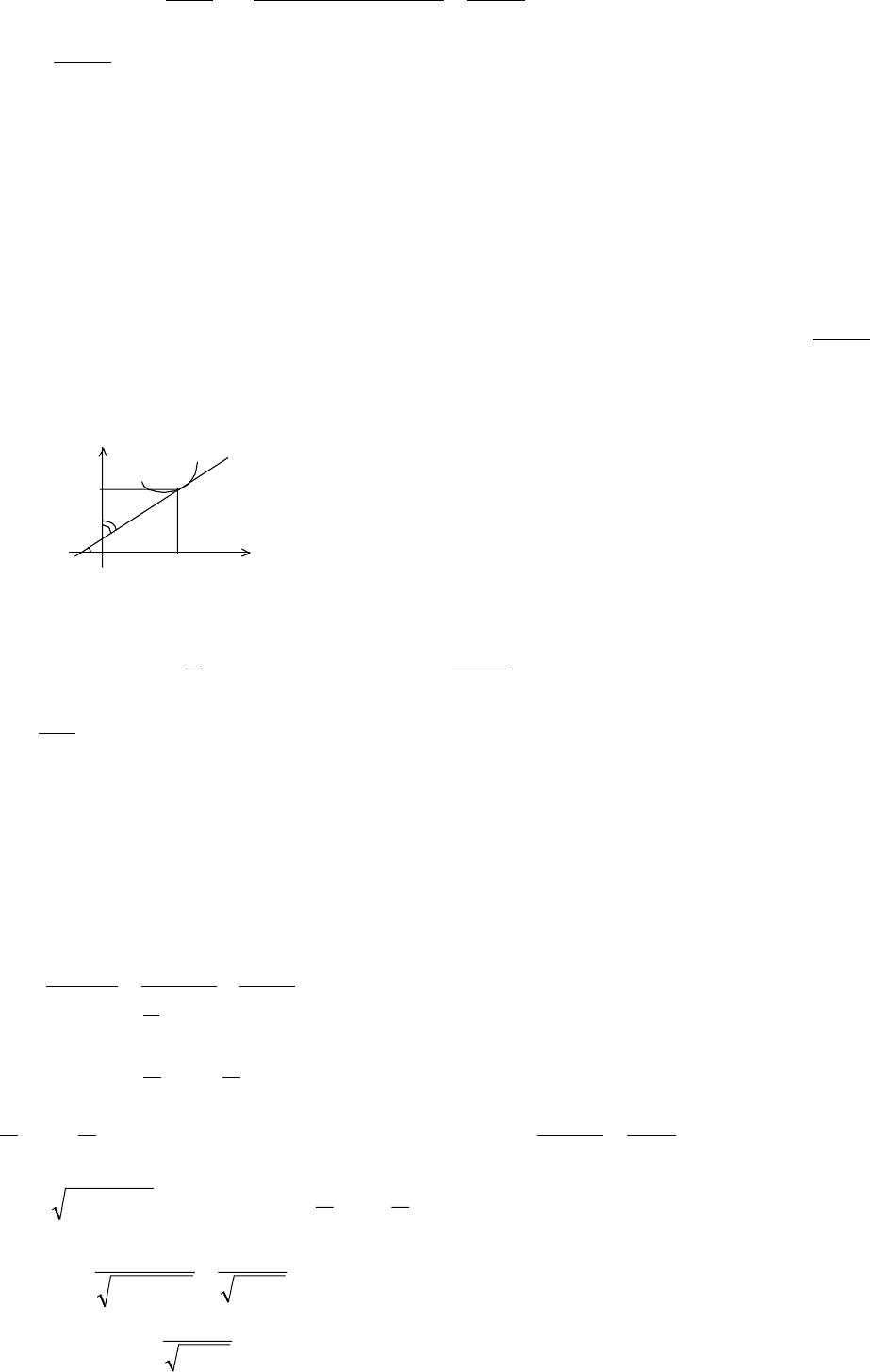
6. y=tgx,
()
()
xx
xxx
x
x
tgx
22
2
cos
1
cos
sinsincos
cos
sin
=
−−
=
′
=
′
(см. теорему 1 п.3.10)
()
x
tgx
2
cos
1
=
′
.
7. y=ctgx. Аналогично этому
Прежде, чем вычислять производные других элементарных функций,
докажем теорему о производной обратной функции.
Теорема.
Пусть функция y=f(x).
1) определена, непрерывна и строго монотонна в некоторой окрестности точки x
0
.
2) в точке x
0
существует отличная от 0 производная
(
)
.0
0
≠
′
xf Тогда и обратная
функция
имеет производную в точке
()
yfx
1−
=
(
)
,
0
x
0
fy
=
причем
()
[]
()
.
1
0
0
1
xf
yf
′
=
′
−
Раскроем геометрический смысл этого положения.
y
0 M
β
α
x
0
x
Рассмотрим в окрестности x=x
0
график
функции y=f(x). Если провести касательную
к графику в точке М(x
0
,y
0
), то
()
α
tgxf =
′
0
(α
- угол наклона касательной к
положительному направлению оси Оx).
()
[]
β
tgyf =
′
−
0
1
(β- угол наклона той
же касательной к положительному направлению оси Оy).
Поскольку
,
2
π
βα
=+ формула
()
[
]
()
0
0
1
1
xf
yf
′
=
′
−
выражает очевидный факт:
.
1
α
β
tg
tg
=
Используя эту теорему, можно получить производные следующих
элементарных функций, являющихся строго монотонными в области их
определения.
8.
Функция
(
10 ≠<= aay
x
)
(
)
+∞<<∞−= xay
x
yx
a
log=
является обратной для
логарифмической функции
, определенной на полупрямой y>0.
Поскольку в окрестности любой точки y выполнены условия теоремы, то
()
()
.ln
log
log
1
1
log
1
aa
e
y
e
y
y
a
x
a
a
a
x
====
′
Итак,
(
)
.ln aaa
xx
=
′
При а=е, получим
(
)
xx
ee =
′
.
9. y=arcsinx,
siny.= xè 1x1- ïðè
22
≤≤≤≤−
π
π
y Будем рассматривать интервал
. 1<x<1- ïðè
22
π
π
<<− y В этом случае
()
()
.
cos
1
sin
1
arcsin
y
y
x
=
′
=
′
Так как
()
22
2
1
1
sin1
1
arcsin
,
22
- èáî 0,>cosy sin1cos
xy
x
yyy
−
=
−
=
′
<<−=
ππ
Итак,
()
2
1
1
arcsin
x
x
−
=
′
.
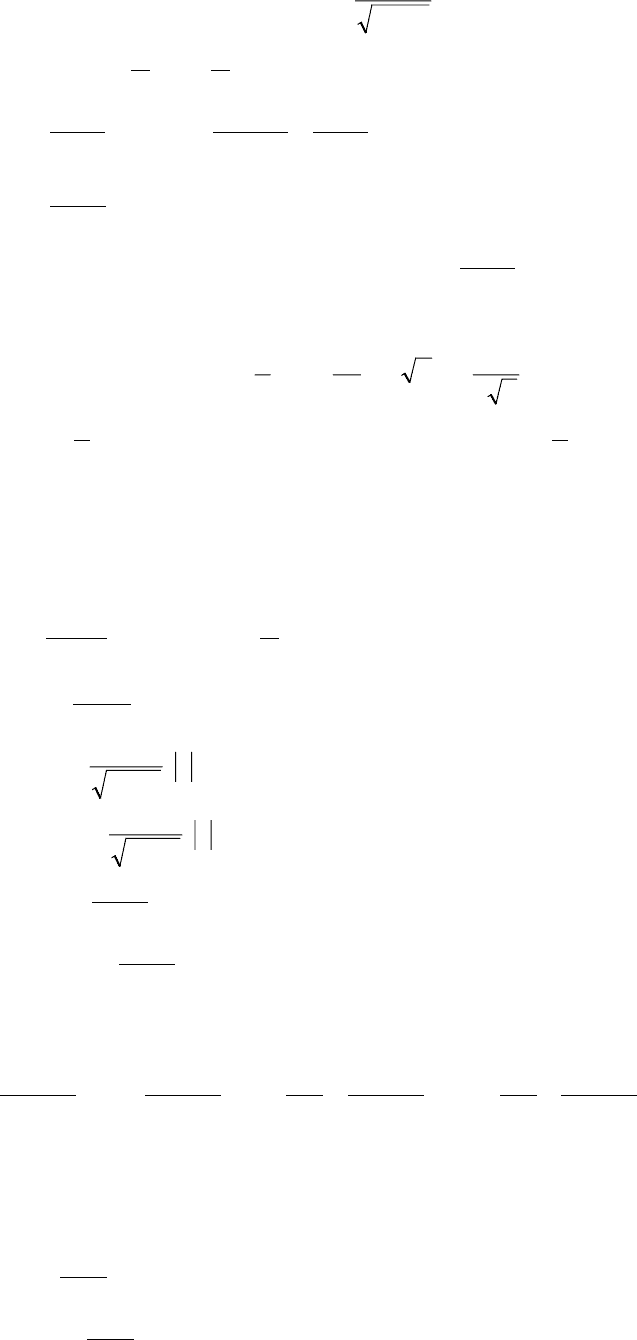
10. Аналогично этому
()
2
1
1
arccos
x
x
−
−=
′
.
11. y=arctgx и
,
22
π
π
<< y− если −∞< x <+∞; x=tgy, тогда
()
()
22
2
1
1
1
1
cos
1
xytg
y
tgy
arctgx
+
=
+
==
′
=
′
()
.
1
1
2
x
arctgx
+
=
′
12. По аналогии с предыдущим
()
.
1
1
2
x
arcctgx
+
−=
′
Сведем теперь в единую таблицу производные элементарных функций.
1.
в частности, ,
1−
=
αα
α
xx
()
()
const
x
x
x
==
′
−=
′
α
2
1
x è
11
2
.
2.
() (
.10 ,0log
1
log ≠<>=
′
axe
x
x
aa
)
В частности
()
.
1
ln
x
x
=
′
3. В частности
()
(
.10ln ≠<=
′
aaaa
xx
)
(
)
xx
ee =
′
.
4.
()
.cossin xx =
′
5.
()
.sincos xx −=
′
6.
()
±±=+≠+==
′
,...2 ,1 ,0 ,
2
,1
cos
1
2
2
kkxxtg
x
tgx
π
π
.
7.
()
()
()
,...2 ,1 ,0 , ,1
sin
1
2
2
±±=≠+−=−=
′
kkxxctg
x
ctgx
π
.
8.
()
.1,
1
1
arcsin
2
<
−
=
′
x
x
x
9.
()
.1,
1
1
arccos
2
<
−
−=
′
x
x
x
10.
()
.
1
1
2
x
arctgx
+
=
′
11.
()
.
1
1
2
x
arcctgx
+
−=
′
По определению, гиперболическим синусом (shx), косинусом (chx),
тангенсом (thx) и котангенсом (cthx) называются функции
,;;
2
;
2
xx
xx
xx
xxxxxx
ee
ee
shx
chx
cthx
ee
ee
chx
shx
thx
ee
chx
ee
shx
−
−
−
−−−
−
+
==
+
−
==
+
=
−
=
производные которых вычисляются по следующим формулам:
13.
()
chxshx =
′
14.
()
shxchx =
′
15.
()
xch
thx
2
1
=
′
16.
()
xsh
cthx
2
1
−=
′
(x≠0).
5.6. Правило дифференцирования сложной функции
Теорема. Пусть
1) задана сложная функция
(
)
[
]
,tfy
ϕ
= где x=ϕ(t) и y=f(x),

2) функция x=ϕ(t) дифференцируема в точке t
0
, а функция y=f(x)
дифференцируема в соответствующей точке x
=ϕ(t ). Тогда сложная функция
0 0
]
()
[
tf
ϕ
дифференцируема в точке t
0
, причем
{}()
[]
()(
.
000
txftf
ϕϕ
′′
=
)
′
Замечание. Обычно формулу для производной сложной функции записывают в
виде
{}
.
()
[]
()
[]
()
000
xxfxf
ϕϕϕ
′
⋅
′
=
′
Пример 1. Найти производную функции
Имеем где x=arctg t.
Поэтому
()
.5
arctgt
y = ,5
x
y =
()
()
.5ln
1
5
2
t
arctgt
+
1
1
5ln555
2
t
arctgt
xxarctgt
=
+
=
′
⋅
′
=
′
Пример 2. Найти производную функции
(
)
(
)
()
()
()
11ln
ln
lnln
lnln
,0,,
−−
⋅=
====
′
⋅=
′
=
′
===
∞∈=∈=
ααα
α
α
α
α
α
α
αα
α
αα
αα
xx
x
eexxtey
eexy
xconstRxy
x
x
xt
tt
xx
5.7. Дифференциал функции
Пусть y=f(x)
∈C
1
(x), тогда ∆y=Α∆x+α(∆x)∆x (1)
Если А
≠0, то слагаемое А∆x есть линейная и однородная относительно ∆x
функция.* При
∆x→0 0lim
0
≠=
∆
∆
→∆
A
x
xA
x
и поэтому А∆x бесконечно малая того же
порядка, что и
∆x.
()
()
,x0=x è 0lim
0
∆∆=
∆
∆
∆
→∆
α
α
x
xx
x
т.е. второе слагаемое α∆x при ∆x→0 есть
бесконечно малая более высокого порядка, чем
∆x. Итак, при А≠0 первое
слагаемое А
∆x является главной частью приращения дифференцируемой
функции.
Определение. При А
≠0 дифференциалом функции y=f(x) в данной толчке x ,
соответствующим приращению аргумента
∆x, называют главную линейную
относительно
∆x часть приращения этой функции в точке x. Символическое
обозначение дифференциала функции y=f(x)dy.
Итак, по определению, dy=A
∆x или
(
)
(
)
xxfxdfdy
∆
′
=
=
(вытекает из теоремы 1
п.4.3.).
Если А=0, то первое слагаемое A
∆x равенства (1) перестает быть главной
частью приращения дифференцируемой функции, ибо A
∆x=0, а α∆x≠0 однако, по
договоренности и в этом случае считают
dy= A
∆x=0.
5.8. Геометрический смысл дифференциала функции
* Функция y=Ax+B, где A≠0 -линейная функция аргумента x, где A и B- некоторые
постоянные. Если В=0, то линейная функция называется однородной.

y
P
k
∆
y
dy
M
∆
x N
T x
x x+
∆
x
Пусть дана кривая y=f(x). Точка М на кривой соответствует значению
аргумента x, а точка Р-(x+∆x). МТ - касательная к кривой y=f(x) в точке М.
Очевидно, что
∆y=PN и dy
()
KNxxf
=
∆
′
=
, откуда вытекает, что величины PN и KN,
вообще говоря, различны, ибо если
∆y есть прира-щение ординаты кривой, то dy
является соответственным приращением ординаты касательной.
5.9. Дифференциал независимой переменной
Под дифференциалом dx независимой x понимают любое, не зависящее от x
число, поэтому, по определению, дифференциалом независимой переменной x
называют ее приращение
∆x, т.е. полагают, что dx=∆x.
Введенное определение оправдывается следующими рассуждениями.
Рассмотрим независимую переменную x как функцию вида y=x, тогда
.
()
x=dx è 1 ∆∆⋅=∆
′
== xxxfdxdy
Таким образом, если аргумент x функции y=f(x) является независимой
переменной, то
() () ()
.
dx
dy
=xf èdx
′′
=∆=
xfxxfdy
Замечание.
- есть число, а
()
xf
′
dx
dy
- отношение неопределенных чисел dy и dx,
которые изменяются пропорционально коэффициентом пропорциональности
.
()
xf
′
5.10. Инвариантность формы первого дифференциала
В предыдущем пункте было показано, что если x - есть независимая
переменная функции y=f(x), то dy=f(x)dx. Покажем, что эта формула справедлива
и в том случае, когда аргумент x является дифференцируемой функцией
некоторой новой переменной t. Это свойство дифференциала называется
инвариантностью его формы.
Итак, пусть дана функция
(
)
(
)
(
)
(
)
.t= xè , tcxcxfy
′
∈
′
∈
=
ϕ
Рассмотрим
сложную функцию y=f[ϕ(t)]. Если рассматривать здесь t как независимую
переменную, то по определению дифференциала функции
()
[]
{}
.dttfdy
′
=
ϕ
(1)
Аналогично этому
(
)
.dttdx
ϕ
′
=
(2)
Используя теорему о сложной функции :
{}()
[]
()
txftf
ϕϕ
′′
=
()
′
равенство (1) можно
переписать в виде
() ()
,dttxfdy
ϕ
′′
=
и из (2) имеем, что
(
)
.dxxfdy
′
=
Итак, в любом случае дифференциал функции y=f(x) может быть записан в форме
будет ли x независимой переменной или нет; разница будет в том, что
()
.dxxfdy
′
=
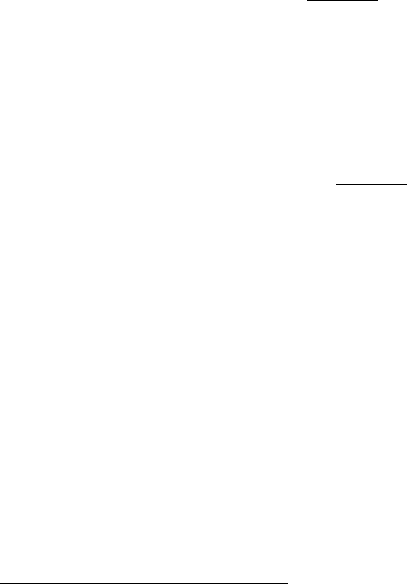
если за независимую переменную выбрано t, то dx означает не произвольное
приращение
∆x, а дифференциал x как функции от t.
5.11. Производные высших порядков
Определение 1. Пусть функция y=f(x) определена на (a,b),
. Производная функции
() ( ){} (
babacxf , xè ,
0
∈
′
∈
)
(
)
xf
′
в точке x
0
называется второй
производной функции f и обозначается
(
)
(
)
(
)
,
00
xxf
′′
f èëè
2
т.е или
.
() ()
[]
0
xx
xfxf
=
′
=
′′
()
′
′
=
′′
yy
Аналогично определяется производная
(
)
n
y любого порядка n=1, 2, ...
Если существует производная
(
)
1−n
y (n-1)-го порядка, то по определению
При этом производная нулевого порядка - сама функция , а
производная первого порядка - производная
()
[]
.
1
′
=
−nn
yy
()
yy =
0
y
′
. Символическая запись
производной n-го порядка функции y=f(x) на
{
}
(
)
(
)
{
}
[
]
xcxf
n
∈:x .
Определение 2. Функция называется n раз дифференцируемой на {x}, если на {x}
она имеет производные до порядка n включительно.
Сформулируем (без доказательства) теорему о вычислении n-ой
производной произведения и суммы двух функций, имеющую большое
прикладное значение.
Теорема.
Пусть функции y
1
=f
1
(x) и y
2
=f
2
(x) определены в некоторой окрестности
точки x
0
, имеют производные n-го порядка в точке x
0
, тогда функции
() () ()
(
)
xfxfyxfxfyy
21212121
y è =+=+
() ()
также имеют производные n-го порядка в
точке x
0
, причем
()
(
)
nnn
yyyy
2121
+=+
()
() () ( ) ()
()
,
()
−−
−
++=
nnnn
y
nn
ynyyyyy
2
1
1
2
1
12121
!2
1
() () ()
∑
=
−
=++
n
i
iini
n
n
yycyyy
0
2121
2
2
... Последняя
формула называется формулой Лейбница.2
Пример. Вычислить
Обозначим
()
()
()
.
2
n
xn
exy = .y è
2
21
xey
x
==
Очевидно, что
() ()
() ()
0......,2,2;
3
2221
======
″
=
′
=
nIYx
k
yyyyxyey
Поэтому,
()
()
()
()
[
]
.122
!2
1
2
22
−++=⋅
−
+⋅+= nnnxxee
nn
xnexey
xxxxn
5.12. Дифференциалы высших порядков
Для удобства проведения дальнейших выкладок для обозначения
дифференциала наряду с символом
α будем употреблять также символ δ (δx и δy).
Пусть
()
(
)
{
}
,,
00
1
δδ
+−∈ xxcxf тогда
(
)
dxxfdy
′
=
. Дифференциал функции dy
есть функция двух переменных: точки x и переменной dx. Пусть, далее,
, и dx имеет одно и то же фиксированное значение для
()
∈
′
=
1
1
cxfy
( ){}
δδ
+−
00
, xx
()
δ
δ
+−∈∀
00
, xxx , тогда
2 Доказательство см.: Ильин В.А., Позняк Э.Г. Основы математического анализа. -М.:
Наука, 1971 (и последующие издания) ч.1.

() ()
[]
()
[]
() ()
.
2
00
0
0
dxxfxdxxfxdxxfdxxfdyS
xx
xx
′′
=
′′
=
′
′
=
′
=
=
=
δδδ
Определение. Значение
δ(dy) дифференциала от первого дифференциала dy в
некоторой точке x
0
, взятое при δx=dx, называют вторым дифференциалом
функции y=f(x) (в точке x
0
) и обозначают символом
()
.d ò.å.,
2
0
22
dxxfyyd
′′
=
Замечание 1. Из определения следует, что d
2
x=0, т.к. приращение ∆x=dx
считается постоянным.
Аналогично определяются дифференциалы более высоких порядков.
Предположим, что производная (n-1)-го порядка
(
)
1−n
y дифференцируема в
окрестности точки x
0
(т.е. функция y=f(x) имеет в точке х
0
производную n-го
порядка), тогда дифференциалом n-го порядка d
n
y функции y=f(x) в точке х
0
называется дифференциал
(
)
yd
n 1−
δ
от дифференциала (n-1)-го порядка d
n-1
y, взятый
при δх=dx, т.е.
(
)
dxx
nn
ydyd
=
−
=
δ
δ
1
.
Методом математической индукции можно получит, что
()
(
)
nnn
dxxfyd
0
= (1)
или
()
()
n
n
n
dx
yd
xf
=
0
(2)
Замечание 2. Формулы (1) и (2) справедливы при n>1 лишь в том случае, когда x
является независимой переменной, т.е. второй и последующие дифференциалы не
обладают, вообще говоря, свойством инвариантности формы. Действительно,
пусть
() {}
[]
()
{
}
[
]
,t= xè
22
tcxcxfy ∈∈=
ϕ
тогда
() ()
[]
()
[]
()
[]
()
[]
() ()
xdxfdxxfxdxxf
xdxxfxdxxfdxxfdyyd
dxx
dxxdxx
dxxdxx
22
2
′
+
′′
=
′
′
+
+
′
′
=
′
′
=
′
==
=
==
==
δ
δδ
δδ
δ
δδδδ
и мы имеем дополнительный, отличный от 0 член
(
)
.
2
xdxf
′
5.13. Дифференцирование функции, заданной параметрически
Пусть функции x=
ϕ(t) и y=ψ(t) определены в некоторой окрестности точки
t
0
. Пусть одна из функций, например,
(
)
(
)
(
)
{
}
(
)()
(
)
,,:
00
↑∧+−∈ tttctt
ϕδδϕϕ
тогда
и в некоторой окрестности точки x
()
xt
1
−
=∃
ϕ
()
0
(x
0
- δ, x
0
+ δ), имеет смысл функция
[
]
.
1
xy
−
=
ϕψ
Функция
()
[
]
xy
1−
=
ϕψ
называется заданной параметрически формулами x=ϕ(t)
и y=
ψ(t) функцией.
Лемма.
() ( )
(
)
()
(
)
(
)
()()
()
[]
() ()()
()
()
()
.
0
0
0
000
11
00
1
0
1
′
′
=
′
∧=∧∈=
⇒≠
′
∧∈∧∈
−
t
t
ytxxcxy
ttcttct
x
ϕ
ψ
ϕϕψ
ϕϕψ
Если x=
ϕ(t) и y=ψ(t) имеют в точке t
0
производные и если
(
)
(
)
[
]
tt
-1
0
=y òî,0
ϕψϕ
≠
имеет в точке x
0
=ϕ(t
0
) производную, причем
(
)
()
0
0
t
t
y
x
ϕ
ψ
′
′
=
′
(1)
Действительно, по правилу дифференцирования сложной функции и
обратной функции имеем:

()
[]
{}
)(
)(1
0
0
1
1
0
0
t
t
tx
txy
tt
t
tt
xt
tt
xx
ϕ
ψ
ψψϕψ
′
′
=
′
′
=
′
⋅
′
=
′
=
′
=
=+=
−
.
Для вычисления второй производной
xx
y
′
′
следует представить ее в виде
()
xxx
y
dx
d
y
′
=
′′
и воспользоваться формулой (1) и правилом дифференцирования частного.
5.14. Свойства дифференцируемых функций
5.14.1. Возрастание (убывание) функций в точке. Локальный экстремум
1. Рассмотрим функцию y=f(x), определенную в некоторой окрестности U(c)
точки С.
Определение 1. Функция f(x) называется возрастающей в точке С, если
существует
δ - окрестность точки c(U
δ
(c)) такая, что
()()
>⇒>
<⇒<
∈∀∧⊂
)()(
)()(
)()()(
cfxfcx
cfxfcx
cUxcUcU
δδ
.
Определение 2. Функция f(x) называется убывающей в точке С, если существует
δ - окрестность точки c(U
δ
(c)) такая, что
()()
<⇒>
>⇒<
∈∀∧⊂
)()(
)()(
)()()(
cfxfcx
cfxfcx
cUxcUcU
δδ
.
Определение 3. Точка с называется точкой локального максимума (локального
минимума) функции f(x) (f(x) имеет локальный минимум в точке С), если
существует такая
δ - окрестность точки c(U (c)) такая, что
δ
()
(
)
()(
.)()()()()(
,)()()()()(
cfxfcUxcUcU
cfxfcUxcUcU
≥⇒∈∀∧⊂
)
≤
⇒
∈
∀
∧
⊂
δδ
δδ
Определение 4. Будем говорить, что функция y=f(x) имеет в точке С локальный
экстремум, если эта функция имеет в точке С либо локальный максимум, либо
локальный минимум (рис.1)
y
y=f(
c
1
c
2
x
x)
Рис. 1
Функция f(x) имеет в точке с
1
локальный максимум, в точке с
2
- локальный
минимум. Заметим, что f(с
1
)<f(с
2
).

Теорема 1. (лемма Ферма) (достаточное условие возрастания (убывания) функции
в точке). Пусть функция f(x) дифференцируема в точке с и
, тогда
y=f(x) возрастает (убывает) в точке С.
)0)((0)( <
′
>
′
cfcf
Замечание 1. Положительность (отрицательность) производной не является
необходимым условием возрастания (убывания) дифференцируемой в точке С
функции y=f(x).
)(cf
′
Пример 1. (рис.2). f(x)=x
3
возрастает в точке С=0, но 03
0
2
0
==
′
== xx
xy
y
y=x
3
x
рис. 2
Теорема 2. (необходимое условие экстремума дифференцируемой в данной точке
функции) (теорема Ферма).
Пусть функция f(x) дифференцируема в точке С и имеет в этой точке
локальный экстремум, тогда
0)(
=
′
cf (рис. 3).
Доказательство. По условию теоремы существует
)(cf
′
. Так как функция y=f(x)
имеет в точке С локальный экстремум, она не может в этой точке ни возрастать,
ни убывать. Следовательно, по теореме 1
)(cf
′
не может быть ни положительной
ни отрицательной, т.е.
. 0)( =
′
cf
Теорема доказана.
y
y=f(x)
x
Рис. 3
Замечание 2. Как показано на рис. 3 касательная к графику дифференцируемой
функции в точке экстремума горизонтальна.
Пример 2. y=x
3
, , но функция не имеет экстремума, т.е. необходимое
условие (теорема 2) экстремума не является достаточным.
0)0( =
′
y
5.14.2. Теорема о нуле производной
Теорема (теорема Ролля).
Пусть функция f(x) непрерывна на сегменте и дифференцируема во всех
внутренних точках этого сегмента, а значения функции на концах сегмента
одинаковы, тогда внутри сегмента найдется такая точка, в которой значение
производной
)(
ξ
f
′
обращается в нуль.
