Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

[]
()( )()
[]
[
]
0)(:),()()()(),(,)(
=
′
∈
∃
⇒
=
∧
′
∃∈∀∧∈
ξ
ξ
fbabfafxfbaxbaCxf .
Доказательство. f(x)∈ C[a,b] (по второй теореме Вейерштрасса) f(x) достигает на
[a,b] своих точных верхней и нижней граней (M и m соответственно). Могут
представиться два случая:
1) M=m; 2) M>m. Рассмотрим оба этих случая.
1) M=m
⇒f(x)=M=m=const⇒ 0)(
≡
′
xf ∀x ∈ [a,b].
2) M>m. Так как f(a)=f(b), хотя бы одно из двух значений M и m достигается во
внутренней точке
ξ сегмента [a,b]. Но тогда функция f(x) имеет в точке ξ
локальный экстремум. По необходимому условию экстремума (теорема Ферма см.
п.5.1)
)(
ξ
f
′
=0. Теорема доказана.
Замечание 3. Кратко можно сказать, что между двумя равными значениями
дифференцируемой функции обязательно лежит нуль производной, то есть
существует хотя бы одна точка, в которой касательная к графику функции
горизонтальна (рис.1).
y
y=f(x)
a
ξ
b x
Рис. 1
Приведем несколько примеров, когда при нарушении хотя бы одного из условий
теоремы утверждение теоремы не имеет места.
а) Функция f(x)=x-E(x) (E(x) - целая часть от x) на сегменте [0,1] не является
непрерывной (рис.2). И хотя все остальные условия теоремы выполнены, однако
на (0,1) не существует точки
ξ такой, чтобы )(
ξ
f
′
=0.
y
1 y=x-E(x)
0 1 x
Рис. 2
б) Нарушено условие дифференцируемости на (а, b)
≤<−
≤≤
=
.21 ,2
10 ,
)(
xx
xx
xf
y
1
0 1 2 x
Рис. 3
в) Нарушено условие f(a)=f(b).
Для функции f(x)=x на [0, 1] (рис.4) нет точки
ξ∈(0, 1), в которой значение
производной обращалось бы в 0.
y
1
0 1 x
Рис. 4
5.14.3. Формула конечных приращений (теорема Лагранжа)
Теорема. Если функция определена и непрерывна на [a,b] и дифференцируема на
(a,b), то внутри сегмента [a,b] найдется точка
ξ такая, что справедлива формула
f(b)-f(a)=
⋅
′
)(
ξ
f (b-a).
()
(
)()
[]
[
]
)()()()(:),()(,],[)( abfafbfbaxfbaxbaCxf −
⋅
′
=
−
∈
∃
⇒
′
∃∈∀∧∈
ξ
ξ
(Формула f(b)-f(a)=
⋅
′
)(
ξ
f (b-a) называется формулой Лагранжа или формулой
конечных приращений).
Доказательство. Рассмотрим на сегменте [a,b] вспомогательную функцию (рис.1)
)(
)()(
)()()( ax
ab
afbf
afxfxF −⋅
−
−
−−= .
Проверим, что для функции F(x) выполнены все условия теоремы Ролля.
1) F(x)
∈C[a,b] (как разность f(x) и линейной функции);
2) ∃ ),(
)()(
)()( bax
ab
afbf
xfxF ∈∀
−
−
−
′
=
′
;
3) F(a)=F(b)=0.
По теореме Ролля
0)(:),(
=
′
∈
∃
ξ
ξ
Fba , т.е.
)()()()(0
)()(
)( abfafbf
ab
afbf
f −⋅
′
=−⇒=
−
−
=
′
ξξ
.
Теорема доказана.
y
C B
A
a
ξ
b x
Рис. 1
Замечание 1. Напишем уравнение прямой l, проходящей через точки A(a, f(a)) и
B(b,f(b)).
)()(
)(
:
afbf
afy
ab
ax
l
−
−
=
−
−
.
Отсюда
)(
)()(
)(: ax
ab
afbf
afy −⋅
−
l
−
+= .
Вычитая эту функцию из f(x), получим F(x), для которой F(a)=F(b)=0.
Угловой коэффициент построенной прямой l равен
ab
afbf
−
−
)()(
. Теорема Лагранжа
утверждает, что найдется такая точка ξ∈(a,b), в которой угловой коэффициент
касательной
)(
ξ
f
′
совпадает с угловым коэффициентом прямой l, т.е. касательная

к графику функции в точке С(ξ,f(ξ)) параллельна прямой l, проходящей через
точки A и В.
Замечание 2. Другой вид формулы Лагранжа.
Пусть х
0
-любое значение аргумента из [a,b], а ∆х- произвольное приращение
аргумента, но такое, что
()
[
]
.,
0
baxx
∈
∆+ Тогда формула Лагранжа для сегмента [x
0
,x
0
+ ∆х] имеет следующий вид:
(
)
(
)
(
)
ξ
fxxfxxf
′
⋅
∆
=
−
∆
+
00
, где ξ- некоторая точка из
интервала
(x
0
,x
0
+ ∆х) (см. рис.2).
x
0
ξ
xx
0
+∆
Рис. 2
Можно утверждать, что найдется такое число
θ (0<θ<1), зависящее от ∆х, что ξ=
x
0
+ θ∆х, тогда
()()
(
)
xxfxxfxxf
∆
+
′
⋅
∆=−
∆
+
θ
000
, гдеθ-некоторое число: 0<θ<1.
Этот вид формулы оправдывает термин “формула конечных приращений”, ибо
дается выражение для приращения функции через вызвавшее его произвольное
конечное приращение
∆х аргумента.
Следствие 1.
() ( )()
(
)
(
)
(
)
[]
(
)
constxfbaxxfbaxxf
=
⇒
∈
∀
≡
′
∧
∈∀
′
∃ ,0,
Доказательство. Пусть x
0
∈(a,b)- фиксированна, x ∈(a,b)- произвольная точка. На
[x
0
, x] (и [x, x
0
] соответственно) f(x) дифференцируема. Применим теорему
Лагранжа на этом сегменте:
(
)
(
)
[
]
(
)
(
)()(
.:,,
0000
xxfxfxfxxxx −⋅
)
′
=
−
∈
∈∃
ξ
ξ
ξ
Но
() () ( ) (
xå.f ò.,0
0
xfxff =⇒=
′
)
.const=
ξ
5.14.4. Обобщенная формула конечных приращений (формула Коши)
Теорема. (теорема Коши)
()
[]
()()
[
]
()
(
)
(
)
(
)()
(
)
(
)
()()()
()()
() ()
() ()
()
()
′
′
=
−
−
∈∃⇒
⇒
≠
′
∈∀∧
∧
′
∃∧
′
∃∈∀∧∈∧∈
ξ
ξ
ξ
g
f
agbg
afbf
ba
xgbax
xgxfbaxbaCxgbaCxf
:,
0,
,,,
(Формула
() ()
() ()
()
()
ξ
ξ
g
f
agbg
afbf
′
′
=
−
−
называется обобщенной формулой конечных
приращений (формулой Коши)).
Доказательство.
1) Докажем, что g(a)
≠g(b). Предположим, что g(a)= g(b), тогда к функции y=g(x)
применима теорема Ролля на сегменте [a,b], по этой теореме
()()
0:, =
′
∈∃
ζ
ζ
gba . Противоречие с условием теоремы
(
)(
., 0 baxxg ∈∀
)
≠
′
Таким
образом, g(a)
≠g(b).
2) Рассмотрим вспомогательную функцию
.
() () ()
(
)
(
)
() ()
() ()
[]
.agxg
agbg
afbf
afxfxF −⋅
−
−
−−=
Для функции F(x) выполнены на сегменте [a,b] все условия теоремы Ролля,
действительно:
1)
()
[]
;,baCxF ∈
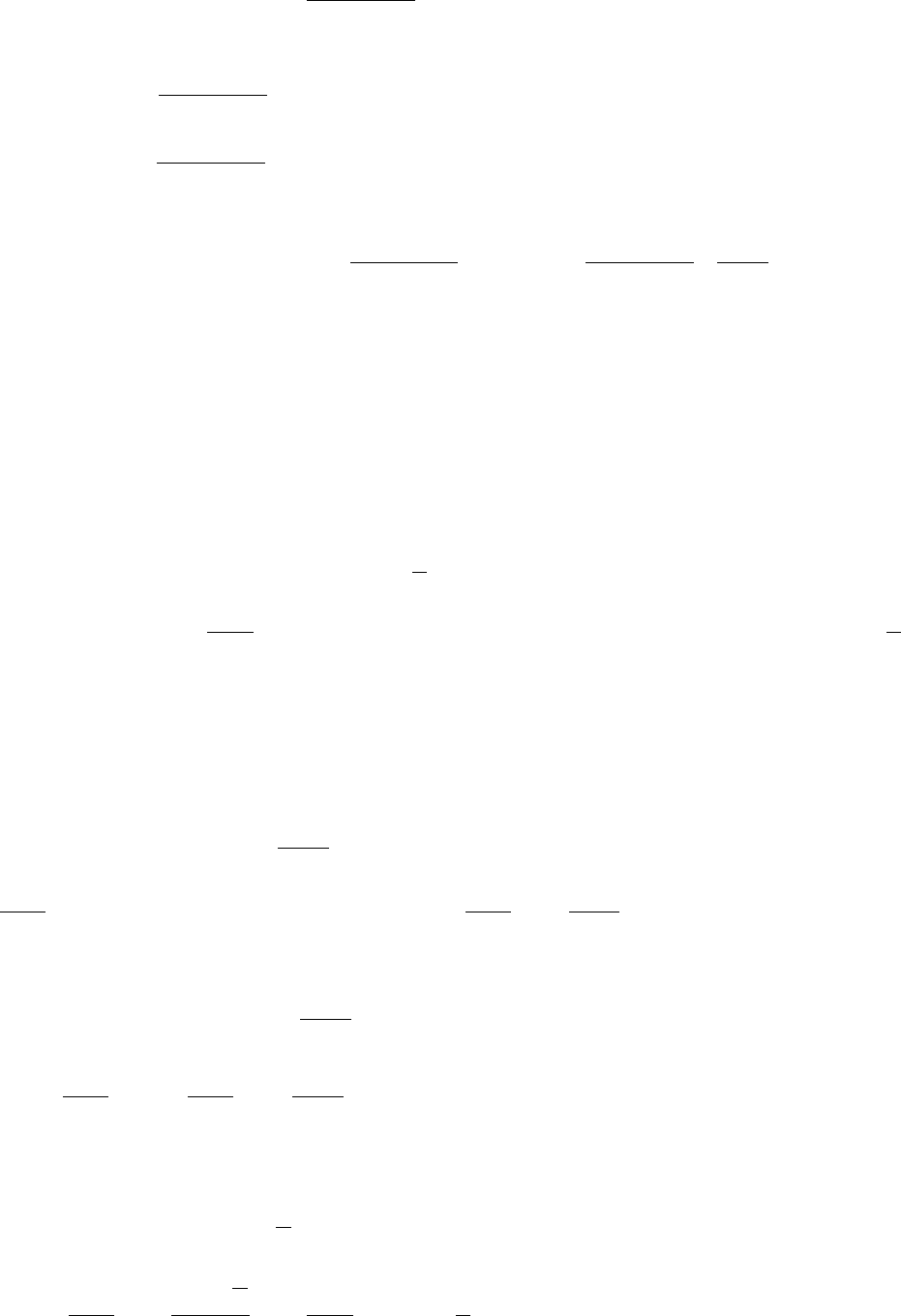
2)
( ) () () ()
()
(
)
() ()
()
;: , xg
agbg
afbf
xfxFxFbax
′
⋅
−
−
−
′
=
′′
∃∈∀
3)
() () ()
() ()
() ()
() ()
[]
() () ()
() ()
() ()
() ()
[]
.0
,0
=−⋅
−
−
−−=
=−⋅
−
−
−−=
agbg
agbg
afbf
afbfbF
agag
agbg
afbf
afafaF
По этой теореме
()
() ()
() ()
() ()
()
() ()
() ()
()
()
ξ
ξ
ξξξ
ξ
g
f
agbg
afbf
g
agbg
afbf
fF
ba
′
′
=
−
−
⇔=
′
⋅
−
−
−
′
⇔=
′
∈
∃
00
:,
Теорема доказана.
Замечание. Формула Лагранжа является частным случаем формулы Коши для
g(x)=x . (Теорема Ролля является частным случаем теоремы Лагранжа лишь
формально, так как доказательство теоремы Лагранжа основано на теореме
Ролля).
5.14.5. Раскрытие неопределенностей (правило Лопиталя)
Раскрытие неопределенностей вида
0
0
.
Будем говорить, что
()
()
xg
xf
представляет собой при x→a неопределенность вида
0
0
,
если
lim
() ()
.0lim
=
=
→→
xgxf
axax
Теорема. (первое правило Лопиталя).
Пусть функции f(x) и g(x) определены и дифференцируемы в проколотой
окрестности точки а. Пусть, кроме того,
(
)
(
)
0limlim
=
=
→→
xgxf
axax
и
()
(
)
aUxxg
$
0 ∈∀≠
′
.
Тогда, если существует
()
()
xg
xf
ax
′
′
→
lim (конечный или бесконечный), то существует
()
()
xg
xf
ax→
lim , причем справедливо равенство
(
)
()
(
)
()
xg
xf
xg
xf
axax
′
′
=
→→
limlim
()
()
()()()
(
)
(
)()()
[]
() ()
()
()
()
()
()
()
()
()
()
′
′
=∧
∃⇒
⇒
′
′
∃∧==∧
∧≠
′
∧
′
∃∧
′
∃∈∀
→→→
→→→
xg
xf
xg
xf
xg
xf
xg
xf
xgxf
xgxgxfaUx
axaxax
axaxax
limlimlim
lim0limlim
0
$
Замечание 1. Предел отношений производных может не существовать, в то
время, как предел отношения функций существует.
Пример 1. а=0,
() ()
xxg
x
xxf sin ,
1
cos
2
==
()
()
0
1
coslim
sin
lim
sin
1
cos
limlim
00
2
0
=⋅⋅==
→→→→
x
x
x
x
x
x
x
xg
xf
xxxax
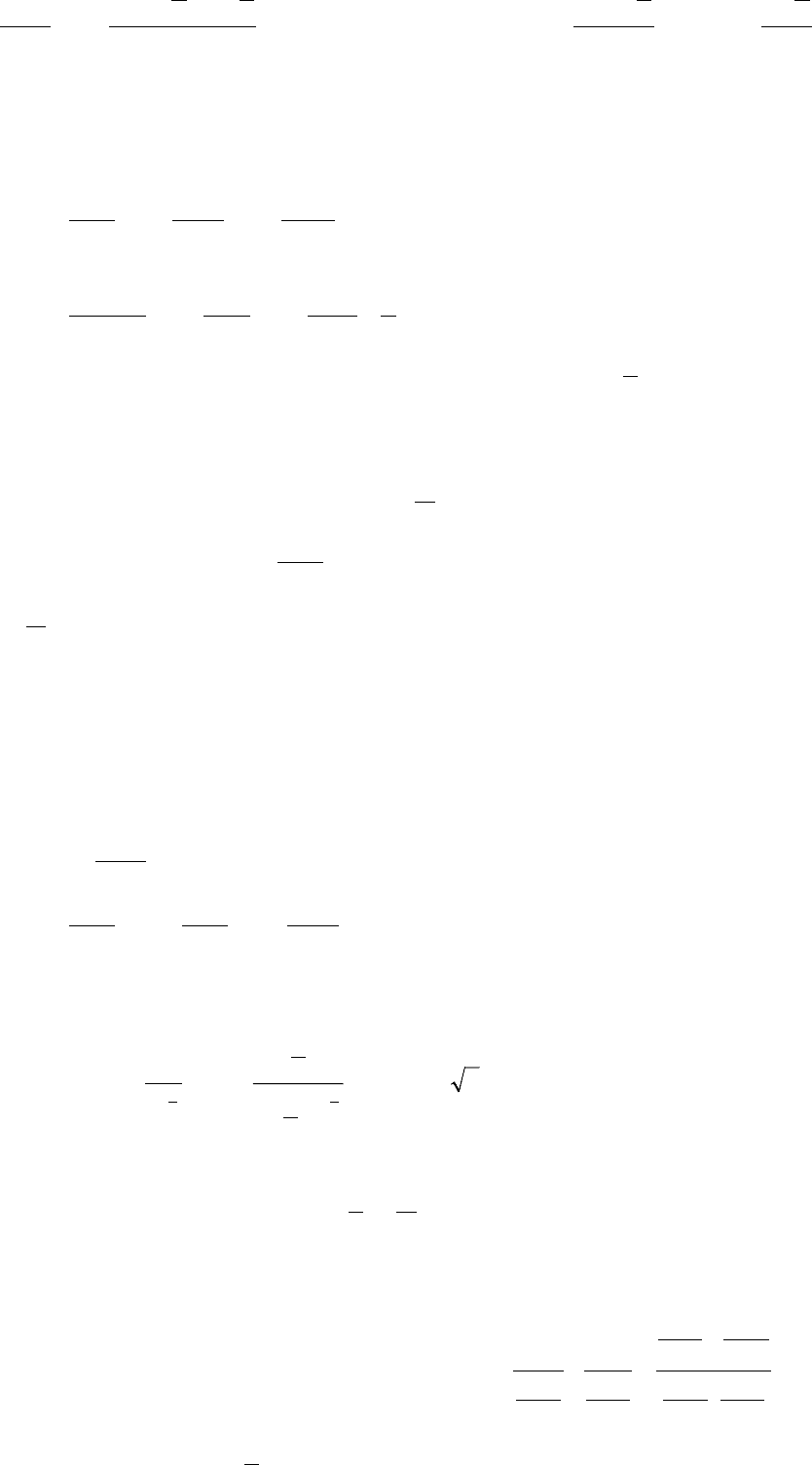
()
()
x
xx
x
xg
xf
axax
cos
1
sin
1
cos2
limlim
+
=
′
′
→→
не существует, так как 0
cos
1
cos2
lim
0
=
→
x
x
x
x
, а
x
x
x
cos
1
sin
0→
lim
не
существует (см. пример 4 п.3.17.).
Замечание 2. Если производные
(
)
(
)
xgxf
′
′
è обладают теми же свойствами, что и
функции f(x) и g(x) , то правило Лопиталя можно применить повторно
()
()
(
)
()
()
()
.limlimlim
xg
xf
xg
xf
xg
xf
axaxax
′′
′′
=
′
′
=
→→→
Пример 2.
2
1
2
cos
lim
2
sin
lim
cos1
lim
00
2
0
===
−
→→→
x
x
x
x
x
xxx
Замечание 3. Правило Лопиталя для неопределенности
0
0
справедливо для
случаев 1) х
→а+0, 2) х→а-0, 3) х → ∞, 4) х → -∞, 5) х → +∞.
Раскрытие неопределенностей вида
∞
∞
.
Будем говорить, что
()
()
xg
xf
представляет собой при х→а неопределенность
вида
∞
∞
, если
() ()
∞
=
∞
=
→→
xgxf
axax
lim ,lim .
Теорема 2. (второе правило Лопиталя).
Пусть функции f(x) и g(x) определены и дифференцируемы в проколотой
окрестности
U точки а и, кроме того,
()
a
;
(
)
(
)
a U0
;
≠
′
xg . Пусть, далее,
() ()
∞
=∞=
→
xf
xax
,lim
→
xg
a
lim
()
()
. Тогда, если существует (конечный или бесконечный
предел)
,lim A
g
f
ax→
x
x
=
′
′
то существует
()
()
(
)
()
()
()
.limlim è lim
ax
xg
xf
xg
xf
xg
xf
axax
′
′
=
→→→
Замечание 4. Второе правило Лопиталя также имеет место для случаев 1) х
→а±0,
2) х
→∞, 3) х→±∞. Изменения в доказательстве аналогичны теореме 1.
Пример 3.
.0lim2
2
1
1
lim
ln
lim
00
2
1
00
2
1
00
=⋅−=
−
=
+→
−
+→
−
+→
x
x
x
x
x
xxx
Раскрытие неопределенностей других видов.
Кроме неопределенностей
∞
∞
è
0
0
()
, часто встречаются неопределенности
вида: 0
.∞, ∞-∞, 1
∞
, ∞
0
, 0
0
. Все эти неопределенности сводятся к изученным выше
двум неопределенностям. Рассмотрим неопределенность вида
∞-∞. Пусть имеем
выражение f(x)-g(x), причем , тогда
()
()
()
() ()
() ()
xgxf
xfxg
xgxf
xgxf
11
11
1
1
1
1
⋅
−
=−=−
, а это
неопределенность вида
0
0
.

Рассмотрим теперь неопределенности типа 1
∞
, 0
0
, ∞
0
. Каждая из этих
неопределенностей имеет вид y=f(x)
g(x)
, где при x→a f(x)→1; 0; ∞, a g(x) →∞; 0; а.
Логарифмируя это выражение (считая, что f(x)>0), получим lny=g(x)lnf(x). В
любом из трех случаев это выражение представляет собой при х→а
неопределенность вида 0
⋅∞.
Покажем теперь, как сводить эту неопределенность к виду
0
0
и
∞
∞
. Итак,
пусть z=
ϕ(x) ⋅ψ(x), причем
∞
=
=
→→
)(lim ,0)(lim xx
axax
ψ
ϕ
)(
1
)(
)(
1
)(
)()(
x
x
x
x
xxz
ϕ
ψ
ψ
ϕ
ψϕ
=−⋅= . Это неопределенности
0
0
и
∞
∞
.
Пример 4.
. Здесь y=x
x
x
x
2
00
lim
−
+→
-2x
, тогда
x
x
xxy
1
ln
2ln2 −=−=ln
1lim0lim2
1
1
lim2
1
ln
)2(limlnlim
2
0000
2
000000
=⇒==
−
−=−=
−
+→+→+→+→+→
x
xxxxx
xx
x
x
x
x
y .
5.14.6. Формула Тейлора с остаточным членом в общей форме (в форме
Шлемильха-Роша)
Теорема. (Тейлора). Пусть функция f(x) имеет в некоторой окрестности точки а
производную порядка n+1 (где n - любой фиксированный номер). Пусть х - любое
значение аргумента из указанной окрестности, р - произвольное положительное
число. Тогда между точками а и х найдется точка
ξ такая, что справедлива
следующая формула:
)()(
!
)(
...)(
!2
)(
)(
!1
)(
)()(
1
)(
2
)2(
xRax
n
af
ax
af
ax
af
afxf
n
n
n
+
+−++−+−
′
+= , (1)
где
()
)(
!
)(
)1(
1
1
ξ
ξ
ξ
+
+
+
−
−
−
=
n
n
p
n
f
pn
x
x
ax
xR . (2)
Формула (1) называется формулой Тейлора с центром в точке
а, а R
n+1
(x) -
остаточный член в общей форме (форме Шлемильха-Роша).
Замечание.
1) Независимо от расположения точки x относительно а (справа или слева от
точки а)
0>
−
−
ξ
x
ax
и для любого p>0 определено
p
x
ax
−
−
ξ
.
2) Функция f(x) и ее производные непрерывны до порядка n включительно.
5.14.7. Остаточный член в форме Лагранжа, Коши, Пеано
Запишем остаточный член в общей форме:
()
)(
!
)(
1
1
1
ξ
ξ
ξ
+
+
+
−
−
−
=
n
n
p
n
f
pn
x
x
ax
xR , где a<ξ<x
a
ξ
x
(x<ξ<a
x
ξ
a
). Отметим, что ξ зависит от x, n, p.
Очевидно, найдется такое число θ (θ зависит от x, n, p): 0<θ<1, что
ξ-a=θ(x-a). Отсюда ξ=a+θ(x-a), x-ξ=(x-a) - θ(x-a)=(x-a)(1-θ) и
[]
[]
)(
!
)1)((
)1)((
)(
)1(
1
1
axaf
pn
ax
ax
ax
xR
n
n
p
n
−+
−−
−−
−
=
+
+
+
θ
θ
θ
.
Итак,
[]
)(
!
)1)((
)(
)1(
1
1
axaf
pn
ax
xR
n
pn
n
−+
−−
=
+
+−
+
θ
θ
.
1. Пусть p=n+1, тогда
[
)(
)!1(
)(
)(
)1(
1
1
axaf
n
ax
xR
n
n
n
−+
+
−
=
+
+
+
θ
]
- остаточный член в форме
Лагранжа.
2. Если p=1, то
[
)(
!
)1()(
)(
)1(
1
1
axaf
n
ax
xR
n
nn
n
−+
−−
=
+
+
+
θ
θ
]
- остаточный член в форме
Коши.
Отметим, что в этих формулах значения
θ, вообще говоря, считаются
различными, так как
θ зависит от р, которое различно в этих формулах.
Сформулируем без доказательства следующую теорему.
Теорема. Пусть функция f(x) имеет производные до порядка (n-1) в некоторой
окрестности точки а и производную порядка n в самой точке а, тогда справедливо
равенство
[
]
n
n
axxR )(0)(
1
−=
+
n
ax )( −
(бесконечно малая при х→а более высокого порядка
малости, чем
). Последняя формула есть остаточный член в форме Пеано.
Замечание. Запишем формулу Тейлора в несколько ином виде:
).(
!
)(
)(
!
)(
...)(
!2
)(
)(
!1
)(
)()(
)1(
1
)(
2
)2(
ξ
ξ
ξ
+
+
−
−
−
+
+−++−+−
′
+=
n
n
p
n
n
f
pn
x
x
ax
ax
n
af
ax
af
ax
af
afxf
Пусть а=х
0
, х-а=∆х. Остаточный член запишем в форме Лагранжа,
тогда
,
)!1(
)(
!
)(
...
!2
)(
!1
)(
)()(
0
)1(
0
)(
2
0
)2(
0
0
x
n
xxf
x
n
xf
x
xf
x
xf
xfxf
n
n
n
∆
+
∆+
+∆++∆+∆
′
=−
+
θ
где 0<
θ<1. При n=0 приходим к формуле Лагранжа:
xxxfxfxf ∆∆+
′
=− )()()(
00
θ
. Таким образом, формула Тейлора является обобщением
формулы Лагранжа.
5.14.8. Формула Маклорена
Формулой Маклорена
называют формулу Тейлора с центром в точке а=0,
т.е. формула Маклорена дает представление функции в окрестности точки х=0.
Формула Маклорена с остаточным членом в форме Лагранжа, Коши и Пеано
имеет вид:
)(
!
)0(
...
!2
)0(
!1
)0(
)0()(
1
2
)2(
xRx
n
f
x
f
x
f
fxf
n
n
+
+
′′
+++
′
+= , где
1) )(
)!1(
)(
)1(
1
1
xf
n
x
xR
n
n
n
θ
+
+
+
+
=
(0<θ<1) (остаточный член, записанный в форме
Лагранжа).
2)
)(
!
)1(
)(
)1(
1
1
xf
n
x
xR
n
nn
n
θ
θ
+
+
+
−
=
(0<θ<1) (остаточный член, записанный в форме
Коши).
3)
(остаточный член, записанный в форме Пеано) )(0)(
1
n
n
xxR =
+
5.14.8.1. Оценка остаточного члена в форме Лагранжа
Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки
х=0 и существует М>0 такое, что
uxMxfNn
n
∈∀≤∈ )(
)(
∀ , тогда
)!1(
)(
1
1
+
≤
+
+
n
x
MxR
n
n
.
Действительно,
)(
)!1()!1(
)(
)(
)1(
1
1)1(
1
xf
n
x
n
xxf
xR
n
n
nn
n
θ
θ
+
+
++
+
+
=
+
=
.
Здесь (0<
θ<1), x∈u⇒θx∈u⇒ Mxf
n
≤
+
)(
)1(
θ
,
поэтому
)!1(
)(
1
1
+
≤
+
+
n
x
MxR
n
n
. (1)
Замечание 1.
0
)!1(
lim
1
=
+
+
∞→
n
x
n
n
при любом фиксированном x.
Докажем это. Положим
!n
x
y
n
n
= , тогда
)!1(
1
1
+
=
+
+
n
x
y
n
n
.
Так как х фиксированно,
()()
()
1
00
+<⇒≥∈∀∈∃ nxnnNnNn .
Пусть n
≥n
0
, тогда
nn
n
n
n
n
yy
n
x
xn
nx
y
y
<⇒<
+
=
+
=
+
+
+
1
1
1
1
1
)!1(
!
,
т.е. начиная с номера n
0
последовательность
{
}
n
y является убывающей. Так как,
кроме того, эта последовательность ограничена снизу ( например, числом нуль),
то по теореме п.2.7. она имеет предел y.
Для нахождения предела заметим, что
n
nn
n
y
n
x
n
x
n
x
n
x
y
11!)!1(
1
1
+
=
+
⋅=
+
=
+
+
.
Переходя к пределу при n
→∞, получим y=0⋅y, т.е. y=0.
Таким образом,
0
)!1(
lim
1
=
+
+
∞→
n
x
n
n
(2)

Замечание 2. Из условий (1) и (2) следует. что, выбирая достаточно большой
номер n, мы можем сделать R
n+1
(x) как угодно малым. Таким образом, если
заменить значение f(x) приближенным, равным
n
n
x
n
f
x
f
f
!
)0(
...
!1
)0(
)0(
)(
++
′
+ ,
то ошибка R
n+1
(x) по абсолютной величине может быть сделана сколь угодно
малой, если только в формуле Маклорена взято достаточно большое число
членов.
5.14.8.2. Разложение по формуле Маклорена некоторых элементарных функций
1) f(x)=e
x
, f
(n)
(x)= e
x
, f
(n)
(0)=1 ∀n∈N,
)(
!
...
!2!1
1
1
2
xR
n
xxx
e
n
n
x
+
+++++= .
Остаточный член в форме Лагранжа равен
)10(
)!1(
)(
1
1
<<
+
=
+
+
θ
θ
x
n
n
e
n
x
xR .
На любом сегменте [-r, r] (r>0) в силу того, что
rrx
eee <≤
θθ
,
получим следующую оценку остаточного члена:
r
n
n
e
n
r
xR
)!1(
)(
1
1
+
<
+
+
.
2) f(x)=sinx. Поскольку
)
2
sin()(
)(
π
mxxf
n
+= (доказывается методом математической
индукции),
,...1,0
12 äëÿ )1(
2k=m äëÿ 0
2
sin)0(
)(
=
+=−
== k
km
mf
k
m
π
(1)
Формула Маклорена имеет вид:
)(
)!12(
)1(...
!7!5!3
sin
32
12753
xR
n
xxxx
xx
n
n
n
+
+
+
+
−++−+−= .
Мы записали R
2n+3
(x), а не R
2n+2
(x), т.к. все члены разложения с четными
номерами в силу (1) равны нулю.
)!32(
cos)1(
)!32(
2
)32(sin
)(
32
132
32
+
⋅−=
+
++
=
+
++
+
n
x
xx
n
nx
xR
n
nn
n
θ
π
θ
.
На любом сегменте [-r, r] (r>0)
)!32(
)(
32
32
+
≤
+
+
n
r
xR
n
n
.
3) f(x)=cosx. Поскольку
)
2
cos()(
)(
π
mxxf
m
+= ,
,...1,0
2 äëÿ )1(
12 äëÿ 0
2
cos)0(
)(
=
=−
+=
== k
km
km
mf
k
m
π
(2)
Формула Маклорена имеет вид:
)(
)!2(
)1(...
!6!4!2
1cos
22
2642
xR
n
xxxx
x
n
n
n
+
+−++−+−= .
Мы записали R
2n+2
(x), а не R
2n+1
(x), т.к. следующий за последним выписанным
слагаемым член многочлена Тейлора в силу (2) равен нулю.
)!22(
cos)1(
)!22(
2
)22(cos
)(
22
22
22
+
⋅−=
+
++
=
+
+
+
n
x
xx
n
nx
xR
n
nn
n
θ
π
θ
На любом сегменте [-r, r]
)!22(
)(
22
22
+
≤
+
+
n
r
xR
n
n
.
4) f(x)=ln(1+x)
)!.1()1()0(f 0,=f(0) ;
)1(
)!1(
)1()(
;...;x)+(-1)(-2)(1=(x)f ;)1)(1()( ;)1(
1
1
)(
1(n)1)(
3-21
−−=
+
−
−=
′′′
+−=
′′
+=
+
=
′
−−
−−
n
x
n
xf
xxfx
x
xf
n
n
nn
Формула Маклорена имеет вид:
)()1(...
432
)1ln(
1
1
432
xR
n
xxxx
xx
n
n
n
+
−
+−++−+−=+ .
Остаточный член запишем в формах Лагранжа и Коши
1
1
1
)1)(1(
)1(
)(
+
+
+
++
−
=
n
nn
n
xn
x
xR
θ
(в форме Лагранжа) (3)
1
1
1
)1(
)1(
)1()(
+
+
+
+
−
⋅−=
n
n
nn
n
x
xxR
θ
θ
(в форме Коши) (4)
Пусть x
∈(0, 1], тогда
1
1
)1)(1(
)(
1
1
1
+
<
++
≤
+
+
+
nxn
x
xR
n
n
n
θ
(следует из (3)),
т.к. x>0,
)0)0(0( 1
1
1
1
1
=⇒=<
+
+
+
n
n
Rx
x
θ
.
Оценим теперь )(
1
xR
n+
на [-r, 0], где 0<r<1.
Будем исходить из формы Коши для R
n+1
(x).
Перепишем этот остаточный член в виде
x
x
x
xR
n
n
n
n
θθ
θ
+
+
−
−=
+
+
11
1
)1()(
1
1
.
Заметим, что
1
1
1
<
+
−
x
θ
θ
для x∈[-r, 0], 0<r<1
1-
θ<1+θx ⇔ θx>-θ ⇔ θx+θ>0 ⇔ θ(x+1)>0 ⇔ x>-1
(что верно по предположению)
r
r
xR
n
n
−
<
+
+
1
)(
1
1
.
Таким образом, R
n+1
(x)→0 при n→∞ ∀x∈[-r, 1], где r<1.
5) f(x)=(1+x)
α
, где α - вещественное число
