Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.


Определение 2. Пусть функция y=f(x) определена для всех x>a (x<a). Прямая
Y=kx+b называется наклонной асимптотой графика функции y=f(x) при х
→ + ∞
(х
→ − ∞), если функция f(x) представима в виде
() () ()
(
)
(
)
0lim 0lim ãäå ,
=
=++=
−∞→+∞→
xxxbkxxf
xx
α
α
α
.
Теорема. Для того, чтобы график функции y=f(x) имел при х→ + ∞
(х
→ −∞) наклонную асимптоту, необходимо и достаточно, чтобы существовали
два предела :
() ()
()
[]
()
[]
(
)
bkxxfbkxxfk
x
xf
k
x
xf
xxx
=−=−
==
−∞→∞→−∞→+∞→
lim lim è lim lim
+x
.
Доказательство. Необходимость. Пусть график функции y=f(x) имеет
асимптоту, для определенности, при х
→ + ∞, т.е. f(x) может быть представлена в
виде
() () ()
0lim , =++=
+∞→
xxbkxxf
x
α
α
() ()
(
)
()
[]
()
[]
bxbkxxf
k
x
x
x
b
k
x
xbkx
x
xf
xx
xxx
=+=−
=
++=
++
=
+∞→+∞→
+∞→+∞→+∞→
α
αα
limlim
limlimlim
Достаточность. Пусть существует
(
)
()
[]
bkxxfk
x
xf
xx
=−=
+∞→+∞→
lim è lim , тогда
f(x)
−kx=b+α(x) и
()
0lim =
+∞→
x
x
α
. Отсюда следует, что f(x)=kx+b+α(x), где α(x) -
бесконечно малая функция при х
→ + ∞.
Замечание. Расположение графика относительно асимптоты при больших х
определяется знаком разности
∆=f(x)−kx−b
∆
>0
∆
<0
∆
меняет знак при
сколь угодно больших х.
При х
→ − ∞ аналогично
∆
>0
∆
<0
∆
меняет знак при
сколь угодно больших по
абсолютной величине х.
Расположение графика относительно вертикальных и наклонных асимптот
позволяет проверить исследование функции на экстремум, а также на
направление выпуклости графика.
5.15.9. Примеры построения графиков функций
Будем проводить построение графиков функций, последовательно отвечая
на вопросы, сформулированные ниже.
1. Построить график функции
(
)
2
2
4−= xxy
1. Область определения:
−∞ < х < +∞;
2. Периодичность: функция не периодическая;
3. Четность: функция не является ни четной, ни нечетной, поскольку f(x)
≠ f(-x) и
f(x)
≠ -f(-x);
4. Точки пересечения с осями ОХ и OY.
с осью ОХ:
с осью OY: ;
=
=
=
=
0
4
0
0
y
x
y
x
=
=
0
0
y
x
5. Непрерывность: функция непрерывна
∀ х∈(−∞,+∞);
6. Асимптоты: функция не имеет ни вертикальных, ни наклонных асимптот;
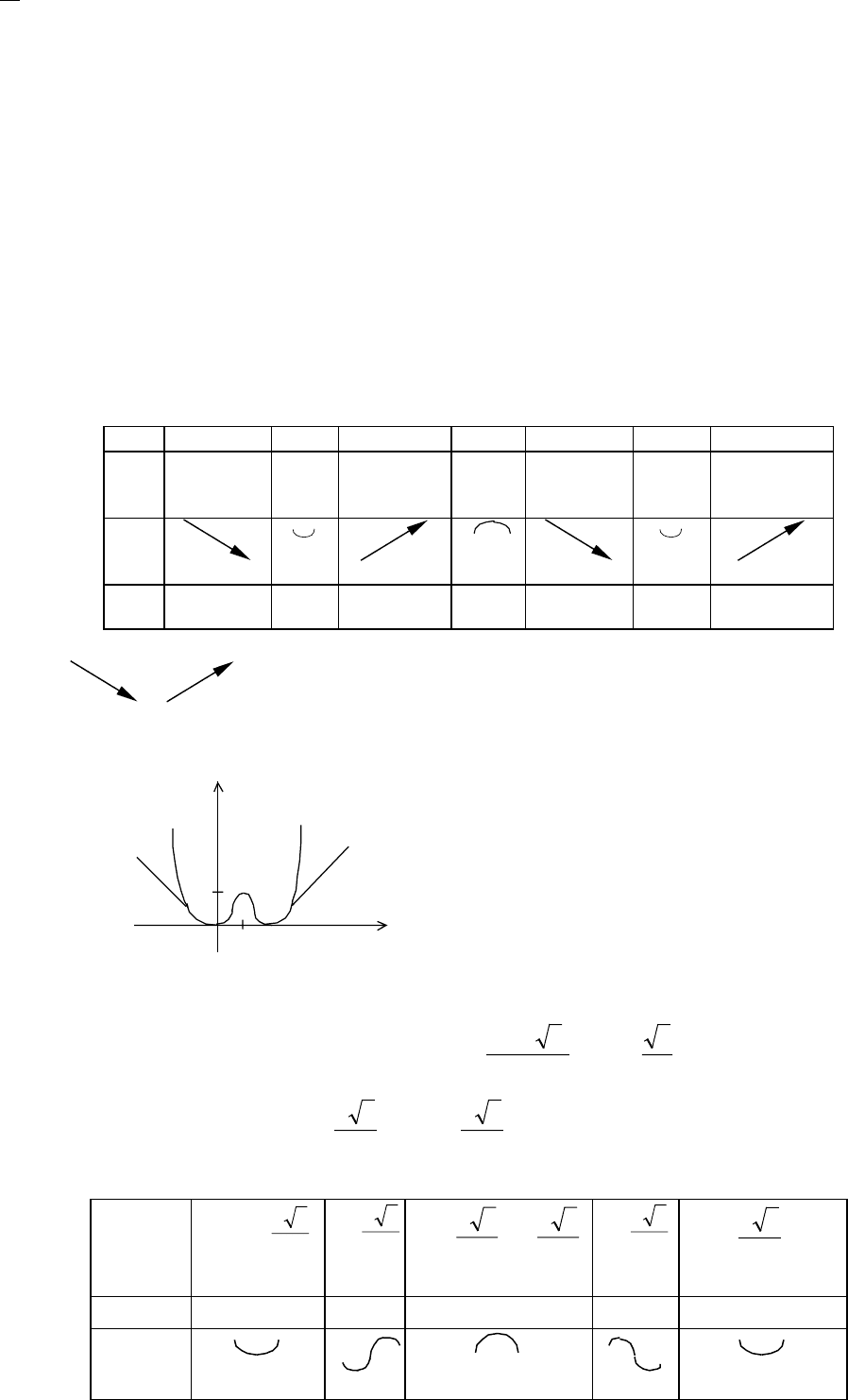
7. Участки монотонности функции, нахождения экстремума.
()() ()()
(
)
(
)
(
)
2444424242
2
2
−−=−+−=−+−=
′
xxxxxxxxxxxxy
Стационарные точки функции: х
1
=0, х
2
=2, х
3
=2.
Составим таблицу
x
(-
∞, 0)
0 (0, 2) 2 (2, 4) 4
(4, ∞)
y
′
—
0
+
0
—
0
+
Рис.
лок.
мин.
лок.
макс.
лок.
мин.
y
0 16 0
Здесь
и
означают убывание и возрастание функции на
соответствующих интервалах.
Примерный график функции представлен на рис.1.
y
1
0 1 2 x
Рис. 1
8. Нахождение точек перегиба:
участки выпуклости вверх и вниз
графика функции. Вычисляем
.
()
xy
′′
(
)
(
)
(
)
(
)( )
[
]
()
()
81234
24864
24424
2
222
+−=
=−+−++−=
=−+
−
+
−
−
=
′
′
xx
xxxxxx
xxxxxxxy
Приравняем нулю
()
(
)
±=
±
−=+−
′′
3
3
12
3
332
;08123 :
2,1
2
xxxxy
Таким образом
()
−−
+−=
′′
3
32
2
3
32
24 xxxy
Составим таблицу
x
−∞−
3
32
2,
3
32
2 −
+−
3
32
2,
3
32
2
3
32
2 +
+∞+ ,
3
32
2
y
′′
+ 0 — 0 +
Рис.
•
•
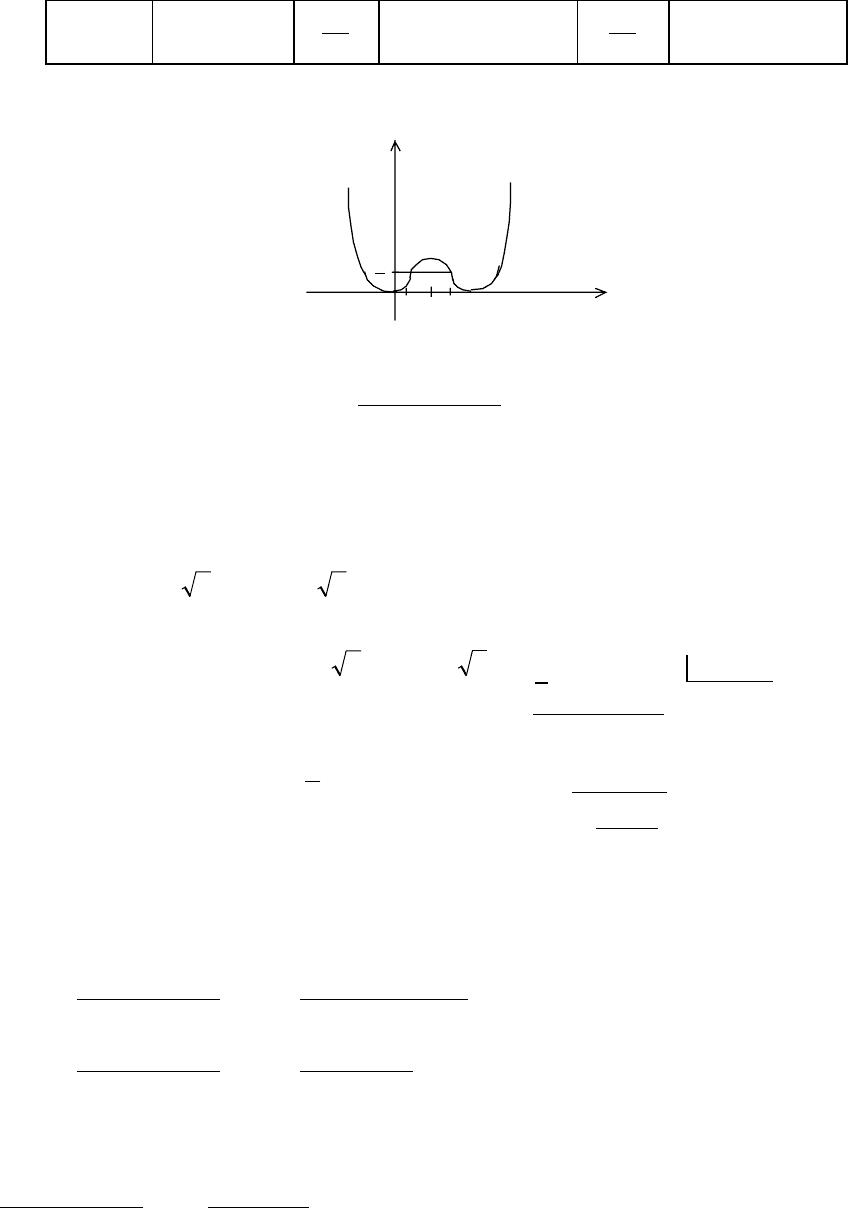
y
9
64
9
64
Окончательный график функции представлен на рис. 2.
y
4
9
0
x
2
2
x
1
x
Рис. 2
3. Построить график функции
1
13
2
23
−
+−+
=
x
xxx
y
1. Область определения: х
≠±1.
2. Четность: функция не является ни четной, ни нечетной.
3. Периодичность: функция не является периодической.
4. Точки пересечения с осями координат:
013
23
=+−+ xxx
21 ,21 ,1
321
+−=−−== xxx
Так как х
≠ 1, то точки пересечения
C осью ОХ
=
+−=
=
−−=
0
21
0
21
y
x
y
x
С осью OY
−=
=
2
1
0
y
x
.
x
3
+x
2
-3x+1 x-1
x
3
-x
2
x
2
+2x-1
2x
2
-3x+1
2x
2
-2x
-x+1
-x+1
0
5. Непрерывность: функция имеет разрывы в точках х=
±1.
Исследуем характер точек разрыва
х=-1;
()
(
)
()()
()
()
−∞=
+
−+
=
−
+−+
+∞=
+−
−+−
=
−
+−+
+−→+−→
−−→−−→
1
12
lim
1
13
lim
11
121
lim
1
13
lim
2
01
2
23
01
2
01
2
23
01
x
xx
x
xxx
xx
xxx
x
xxx
xx
xx
Точка х=-1 - точка разрыва 2-го рода
Пусть х=1
1
1
12
lim
1
13
lim
2
0
2
23
01
=
+
−+
=
−
+−+
±→±→
x
xx
x
xxx
xx
Точка х=1 - точка устранимого разрыва.
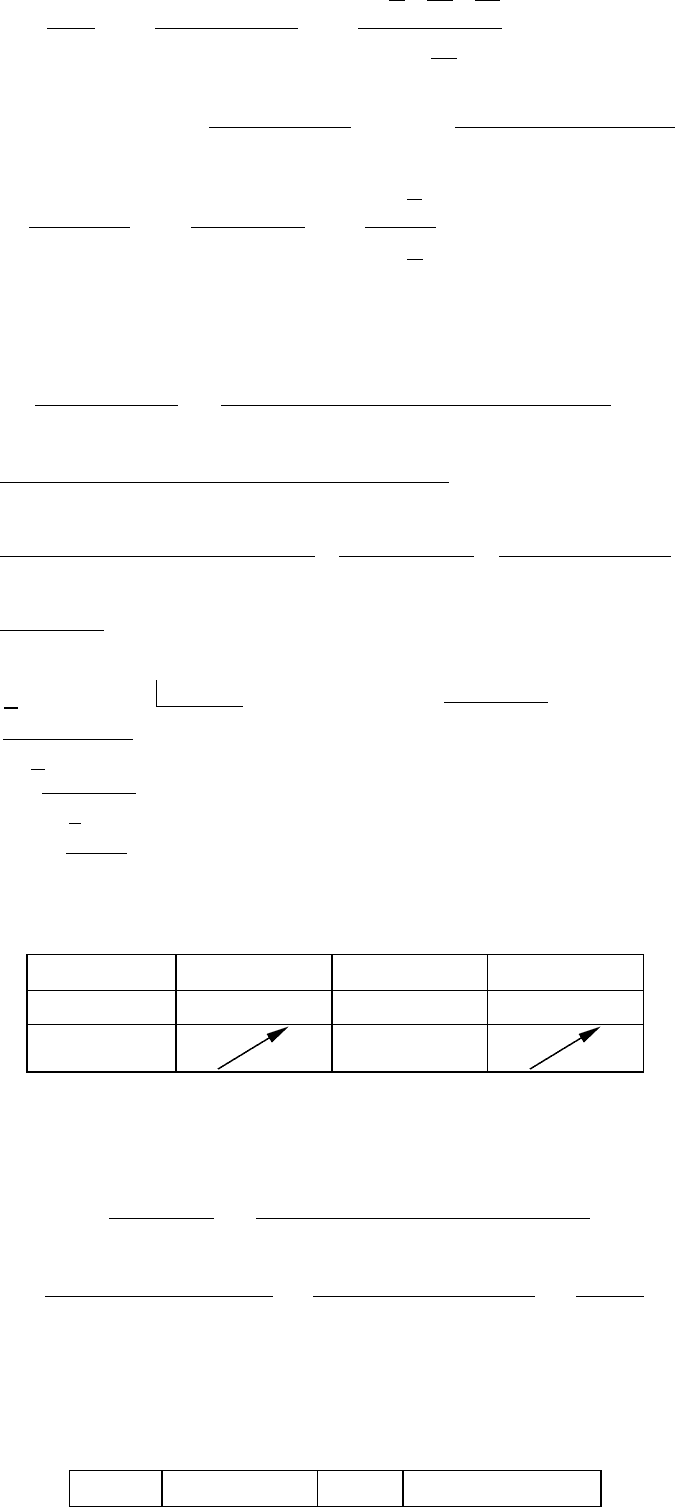
6. Асимптоты.
х=
−1 - вертикальная асимптота.
Наклонные асимптоты.
()
()
()
[]
()
()()
1
1
1
1
1
lim
11
1
lim
1
12
lim
1
13
lim
1
13
limlim
1
1
1
131
1
lim
1
13
limlim
2
2
2
2
323
2
23
2
32
2
23
=
+
−
=
+−
−
=
−
+−
=
=
−
+−+−+
=
−
−
−−+
=−=
=
−
+−+
=
−
+−+
==
∞→∞→∞→
∞→∞→∞→
∞→∞→∞→
x
x
xx
x
x
xx
x
xxxxx
x
x
xxx
kxxfb
x
xxx
xx
xxx
x
xf
k
xxx
xxx
xxx
Уравнение наклонной асимптоты у=х+1.
7. Участки монотонности, локальный экстремум функции.
(
)
(
)
(
)
()
()
()()()
()
()()
()() ()()
()
()
()()
()
2
2
2
2
2
23
2
2323
22
22
2
2
2322
2
23
1
32
11
321
11
3
11
242353
11
121211323
1
2131323
1
13
+
++
=
=
+−
++−
=
+−
−++
=
+−
+−−−−+
=
=
+−
−+−−+−−+
=
=
−
+−+−−−+
=
′
−
+−+
=
′
x
xx
xx
xxx
xx
xxx
xx
xxxxxx
xx
xxxxxxxx
x
xxxxxxx
x
xxx
y
x
3
+x
2
+x-3 x-1
x
3
-x
2
x
2
+2x+3
2x
2
+x-3
2x
2
-2x
3x-3
3x-3
0
Итак,
()
()
2
2
1
32
+
++
=
′
x
xx
xy
Отсюда следует, что
()
0 ≠
′
∀
xyx и
стационарных точек функция не
имеет.
При х=
−1
(
)
xy
′
не существует.
Составим таблицу
x
(-
∞, -1)
-1
(-1, ∞)
y
′
+ не сущ. +
Рис.
8. Нахождение точек перегиба; участки выпуклости вверх и вниз графика
функции.
()
()
()()
()
()
()
()
()
()
() ()
33
222
2
3
2
2
2
1
4
1
3212
2
31
32212
1
1232122
1
32
+
−=
+
−−−+−
=
+
++−+
=
=
+
+++−++
=
′
+
++
=
′′
xx
xxxx
x
xxx
x
xxxxx
x
xx
xy
()
(
)
(
)
(
)
() ( ) ( )
∞−∪−∞−∈∀≠
′′
∞
−
∈
∀
<
′
′
−
∞
−
∈
∀>
′′
,11,0
,1 0xy è 1, 0
xxy
xxxy
Составим таблицу
x
(-
∞, -1)
-1
(-1, ∞)
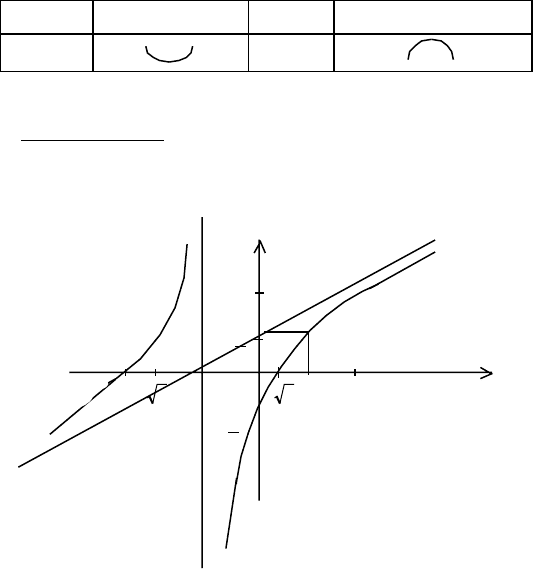
y
′′
+ —
Рис.
График функции
22
13
2
23
−
+−+
=
x
xxx
y
приведен на рис. 4
y
1
1
2
-1 -
2
1 1+
2
1 2
x
-
1
2
-1
Рис. 4
6. Неопределенный интеграл
6.1. Первообразная функция
Пусть функция f(x) определена на множестве М, которое является либо
интервалом (конечным или бесконечным), либо сегментом.
Замечание. Рассмотрение сегмента необходимо для применения
неопределенного интеграла в дальнейшем для вычисления определенного
интеграла.
Определение. Функция F(x) называется первообразной (функцией) для функций
f(x) на множестве М, если она дифференцируема в каждой точке х множества М и
.
Mx )x(f)x(F ∈∀=
′
Замечание. В концевых точках сегмента рассматриваются односторонние
производные.
Пример. f(x)=2x
⇒ ),(x x)x(F
2
+∞−∞∈∀=
Действительно:
),(x x2)x(F
+
∞
−
∞
∈
∀
=
′
Очевидно, что если F(x) является первообразной для функций f(x) на множестве
М, то F(x)+C (C = const) также является первообразной для f(x) на множестве М
.
[]
=
′
=
′
+ )x(f)x(FC)x(F
Теорема 1. Пусть F
1
(x) и F
2
(x) - любые первообразные для функции f(x) на
множестве М, тогда F
1
(x) - F
2
(x) = С ∀x ∈ M, где С = const.
Доказательство. Положим, G(x)= F
1
(x) - F
2
(x), тогда G(x) дифференцируема на М
(в случае сегмента в концевых точках существуют односторонние производные) и
()
Mx 0)x(f)x(f)x(F)x(F)x(F)x(F)x(G
2121
∈∀=−=
′
−
′
=
′
−=
′
,
откуда следует, что G(x)=C =const Mx
∈
∀
, т.е.
F
1
(x) - F
2
(x) ≡ С=const Mx
∈
∀
.
Теорема доказана. Таким образом показано, что любые первообразные для одной
и той же функции на множестве М могут отличаться лишь на константу.
Следствие. Если F(x) - одна из первообразных для f(x) на множестве М, то любая
первообразная
Φ(х) для f(x) на М представляются в виде Φ(х)=F(x)+C, где С -
некоторая константа.
6.2. Неопределенный интеграл
Определение. Совокупность всех первообразных функций f(x) на множестве М
называется неопределенным интегралом от функции f(x) (на этом множестве) и
обозначается символом
∫
dx)x(f
В этом обозначении знак
∫
называется знаком интеграла, выражение f(x)dx
- подынтегральным выражением, а функция f(x) - подынтегральной функцией.
Если F(x) - одна из первообразных функций для функции f(x) на множестве
М, то в силу следствия из теоремы п.1.1.
∫
+= C)x(Fdx)x(f
(1)
где С - любая постоянная. Это равенство следует понимать как равенство двух
множеств, точнее следовало бы записать так:
{
}
∫
+= C)x(Fdx)x(f
.
Пример. .
+∞<<∞−+=
∫
x Cxsindxcos
Замечание. Если F(x) - первообразная функции f(x) на множестве М, то в
формуле (1) под знаком интеграла стоит дифференциал функции F(x),
действительно:
dx)x(fdx)x(FdF =
′
=
.
Будем считать по определению, что
∫
∫
∫
≡
′
≡ )x(dFdx)x(Fdx)x(f
(2)
6.3. Основные свойства неопределенного интеграла
1
0
. Пусть функция F(x) дифференцируема на М, тогда
()
(
)
(
)
(
)
∫
∫
+=
′
+= cxFdxxF èëè cxFxdF
Cправедливость этих равенств вытекает из соотношений (1), (2) п.1.2.
2
0
. Пусть функция f(x) имеет первообразную на множестве М, тогда
(
)
(
)
∫
= dxxfdxxfd
Здесь под интегралом понимается любая первообразная F(x) функции f(x).
Справедливость этой формулы очевидна в силу определения первообразной: так
()
∫
dxxf
() ()
(
)
(
)
[
]
(
)
(
)()
∫∫
=
′
==+=⇒+= dxxfdxxFxdFcxFddxxfdcxFdxxf
.
3
0
. Если функции f
1
(x) и f
2
(x) имеют первообразные на М, то и функция
f
1
(x) + f
2
(x) также имеет первообразную на М, и
() ()
[]
(
)
(
)
∫
∫
∫
+=+ dxxfdxxfdxxfxf
2121
(1)
Это равенство означает совпадение двух множеств функций, т.е., что сумма
каких-либо первообразных для функций f
1
(x) и f
2
(x) является первообразной для
функции f
1
(x) + f
2
(x), и наоборот, всякая первообразная для функции f
1
(x) + f
2
(x)
является суммой некоторых первообразных для функций f
1
(x) и f
2
(x).
Доказательство. Пусть
()
(
)
(
)
(
)
∫
∫
+=+= ;cxFdxxf,cxFdxxf
222111
Положим F(x)=F
1
(x)+F
2
(x), тогда F(x) дифференцируема на М и
() () ()( ) () () () ()
,Mx xfxfxFxFxFxFxF
212121
∈∀+=
′
+
′
=
′
+=
′
т.е F(x) является первообразной функции f
1
(x) + f
2
(x) на М. Таким образом,
()
(
)()
(
)
(
)
(
)
∫
++=+=+ ,cxFxFcxFdxxfxf
2121
() ()
(
)
(
)
(
)
(
)
∫∫
+++=+++=+
2121221121
ccxFxFcxFcxFdxxfdxxf
Так как с
1
+с
2
- также произвольная постоянная, то множества
() (){ } () (){
cxFxF è ccxFxF
212121
}
+
++++
совпадают.
Свойство 3
0
доказано. Аналогично доказывается, что
()
(
)
[]
(
)
(
)
∫
∫
∫
−=− dxxfdxxfdxxfxf
2121
.
4
0
. Если функция f(x) имеет первообразную на М и а∈R, то функция аf(x) также
имеет на М первообразную, причем а
≠0 имеет место равенство
()
(
)
∫
∫
= dxxfadxxaf
(2)
Доказательство. Пусть
()
(
)
cxFdxxf +=
∫
, тогда
()() ()(
xafxFaxaF =
′
=
)
′
. Таким образом
() ()()()
(
)
(
)
cxxaFcxFadxxfa
1
+=+=
∫
.aFdxxaf ,ac =+
∫
Так как а
≠0, то ас также является произвольной постоянной, и множества
совпадают. Свойство 4
(){}(){
cxaF,acxaF ++
}
0
доказано.
Свойства 3
0
и 4
0
выражают свойства линейности неопределенного интеграла
относительно подынтегральной функции.
Вопрос о существовании первообразных остается пока открытым.
6.4. Таблица основных неопределенных интегралов
Ранее мы получили таблицу. Каждая формула таблицы производных
простейших элементарных функций, устанавливающая, что та или иная функция
F(x) имеет производную f(x), приводит нас, в силу определения неопределенного
интеграла, к соответствующей формуле интегрального исчисления
(
)
(
)
cxFdxxf +=
∫
Таким образом, приходим к следующей таблице интегралов.
1.
cdx0 =⋅
∫
2.
cxdx1 +=⋅
∫
3.
()
1 c
1
x
dxx
1
−≠+
+
=
+
∫
α
α
α
α
4.
()
() ()
[]
()
∫
=−⋅−=
′
−=
=
′
=
+=
x
1
1
x
1
x-ln è xlnxln 0< xÏðè
.
x
1
lnx è xlnxln 0> xÏðè
cxln
x
dx
5.
()
cedxe ,1a0 c
aln
a
dxa
xx
x
x
+=≠<+=
∫∫

6.
cxcosxdxsin +−=
∫
7.
cxsinxdxcos +=
∫
8.
∫
Π∈+≠+= n ,n
2
x ctgx
xcos
dx
2
π
π
9.
()
∫
Π∈≠+−= n ,nx cctgx
xsin
dx
2
π
10.
∫
+−
+
=
−
cxarccos
cxarcsin
x1
dx
2
(-1<x<1)
11.
∫
+−
+
=
+
carcctgx
carctgx
x1
dx
3
12.
∫
+±+=
±
c1xxln
1x
dx
2
2
(x>1 в случае знака “−“)
13.
()
∫
≠+
−
+
=
−
1x c
x1
x1
ln
2
1
x1
dx
2
14.
cchxshxdx +=
∫
15.
∫
+= cshxchxdx
16.
∫
+= cthx
xch
dx
2
17.
∫
+−= cchx
xsh
dx
2
Замечание 1. Доказательство формул 12 и 13 следует провести
непосредственным дифференцированием правых частей и проверкой совпадения
результата с подынтегральными функциями слева.
Замечание 2. Операция дифференцирования не выводит нас из класса
элементарных функций, однако можно доказать, что интегралы от некоторых
элементарных функций уже не являются элементарными функциями, например,
∫
−
dxe
2
x
- интеграл Пуассона.
Теорема 2. Пусть функция
ϕ(х) определена и дифференцируема на множестве М.
Пусть, далее, для функции g(u) существует первообразная функции G(u) на
множестве
()
{}
MxxU ∈=
ϕ
,т.е
(
)
(
)
cuGduug +=
∫
.
Тогда на множестве М для функции
(
)
(
)
(
)
xxg
ϕ
ϕ
′
⋅
существует первообразная, равная
G[ϕ(x)], т.е.
()()
(
)
(
)
(
)
()()() ()
()
∫
∫
∫
=
=
′
+=
′
xu
duugdxxxg
èëè
cxGdxxxg
ϕ
ϕϕ
ϕϕϕ
(1)
Доказательство. По теореме о производной сложной функции имеем
()(){}()
()
()
xuGxG
dx
d
xuu
ϕϕ
ϕ
′
⋅
′
=
=
.
Но
G по определению первообразной есть g(u), поэтому
()
u
u
′
()(){}()
()
() ()()(
xxgxugxG
dx
d
xu
ϕϕϕϕ
ϕ
′
⋅=
′
⋅=
=
)
.

Таким образом, G(ϕ(x)) является первообразной функции
()()
(
)
xxg
ϕ
ϕ
′
⋅
на
множестве М, и формула (1) доказана.
Существует два варианта метода замены переменной.
а) Метод подведения под знак дифференциала.
Пусть требуется вычислить интеграл
(
)
∫
dxxf
. Предположим, что существует
дифференцируемая функция
ϕ(х) и функция g(u) такие, что подынтегральное
выражение f(x)dx может быть записано в виде
() ()()
(
)
(
)
(
)
(
)
(
)
duugxdxgdxxxgdxxf
=
=
′
⋅
=
ϕ
ϕ
ϕ
ϕ
(это преобразование называется подведением ϕ(х) под знак дифференциала). По
теореме 2 имеем
()
(
)
(
)
(
)
(
)
()
∫
∫
∫
=
=
′
=
xu
duugdxxxgdxxf
ϕ
ϕϕ
Поэтому вычисление сводится к вычислению интеграла (который
может оказаться проще исходного) и последующей подстановке u=
ϕ(x).
()
∫
dxxf
()
∫
duug
Пример.
∫∫∫
+=+===⋅
==
c
4
xsin
c
4
u
duuxsinxdsinxdxcosxsin
4
xsinu
4
xsinu
333
Пример.
(
)
(
)
∫∫ ∫∫
==
−+
−+
=
−+
+
=
−+
+
−+= 3xxu
2
2
2
2
2
2
u
du
3xx
3xxd
3xx
xxd
dx
3xx
1x2
c3xxlnculn
2
3xxu
2
+−+=+=
−+=
.
б) Метод подстановки. Пусть требуется вычислить интеграл
. Введем
новую переменную u формулой x=
ϕ(u), где ϕ(u) строго монотонная,
дифференцируемая функция.
∫
dx)x(f
Подставим x=
ϕ(u) в исходное подынтегральное выражение, получим
() ()( ) () ()
duugduuufdxxf
=
′
⋅=
ϕ
ϕ
По теореме 2 справедливо равенство
() ()()() ()
()
∫∫∫
−−
==
=
′
⋅=
xu)x(u
11
duugduuufdxxf
ϕϕ
ϕϕ
т.е. вычисление интеграла
сводится к вычислению интеграла
∫
dx)x(f
∫
du)u(g
(который может оказаться проще исходного) и последующей подстановке u=
ϕ
-
1
(x)
Пример
∫
+
+
dx
x1
x1
()
, x>0. Положим x=u
2
u∈(0,+∞); u
2
строго монотонна на этом
множестве
x)x(u ,udu2duudx
12
===
′
=
−
ϕ
, откуда
∫∫∫∫
=
+
−+−=
+
+
=
+
+
1u
du
4du)2uu(2du
1u
uu
2dx
x1
x1
2
3
()
=+
+−
+−=
=
c1uln4u2u
2
1
u
3
1
2
xu
23
(
)
c1xln4x2x
2
1
x
3
1
2
2123
++−
+−=
.
Конечно, такой прием применим не ко всякому интегралу. Кроме того,
следует подчеркнуть, что выбор правильной подстановки в значительной мере
определяется искусством вычислителя.
Рассмотрим еще один пример, который позволит нам расширить таблицу
интегралов
=
+
=
+
=
+
=
+
∫∫∫∫
=
a
x
u
2
22
222
u1
du
a
1
a
x
1
a
x
d
a
1
a
x
1
dx
a
1
xa
dx
c
a
x
arctg
a
1
c
a
x
arctg
a
1
carctgu
a
1
a
x
u
+−=+=+=
=
Аналогично вычисляются следующие интегралы:
c
ax
ax
ln
a2
1
ax
dx
22
+
+
−
=
−
∫
∫
<+−=+=
−
ax ,c
a
x
arccosc
a
x
arcsin
xa
dx
22
.
caxxln
ax
dx
22
22
+±+=
±
∫
6.5. Интегрирование по частям
Теорема. Пусть функции u(x) и v(x) дифференцируемы на множестве М и, кроме
того, на этом множестве существует первообразная для функции
. Тогда
на множестве М существует первообразная для функции
и справедлива
формула
)x(u)x(v
′
)x(v)x(u
′
∫
∫
′
−⋅=
′
dx)x(u)x(v)x(v)x(udx)x(v)x(u
(1)
Замечание 1. В концевых точках множества М (если М - сегмент)
рассматриваются односторонние производные.
Замечание 2. Определение дифференциала и свойство инвариантности его
формы позволяют записать эту формулу в виде
∫
∫
−= vdu)x(v)x(uudv
Доказательство теоремы. Запишем формулу для производной произведения
функций u(x) и v(x).
[] []
)x(v)x(u)x(v)x(u)x(v)x(u );x(v)x(u)x(v)x(u)x(v)x(u
′
−
′
=
′′
+
′
=
′
.
Умножим последнее равенство на dx и возьмем интеграл от обеих частей
полученного равенства. Так как по условию на М существует
[]
∫∫
+=
′
′
c)x(v)x(udx)x(v)x(u è ,dx)x(u)x(v
, то на М существует
∫
′
dx)x(v)x(u
и справедлива формула
∫
∫
′
−+⋅=
′
dx)x(v)x(uc)x(v)x(udx)x(v)x(u
Включая произвольную постоянную С в
∫
′
dx)x(v)x(u
, получим формулу (1).
Формула (1) сводит вопрос о вычислении интеграла к вычислению
интеграла
. В ряде конкретных случаев этот последний интеграл проще
исходного.
∫
udv
∫
vdu
