Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

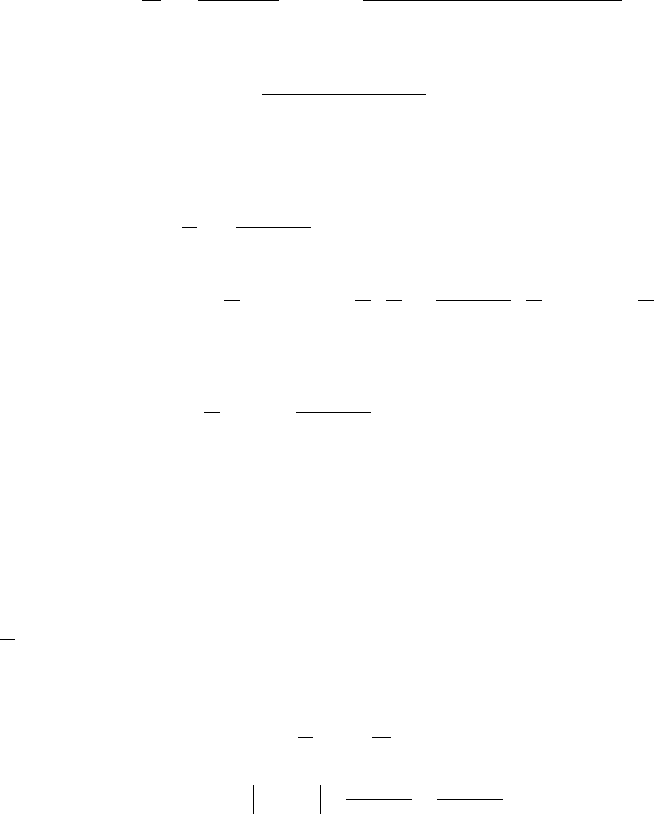
).1)...(1()0(
,)1)(1)...(1()(
)(
)(
+−−=
++−−=
−
nf
xnxf
n
nn
ααα
ααα
α
Формула Маклорена имеет вид:
)(
!
)1)...(2)(1(
...
!2
)1(
!1
1)1(
1
2
xRx
n
n
xxx
n
n
+
+
+
−
−
−
++
−
++=+
α
α
α
α
α
α
α
α
,
где остаточный член в форме Лагранжа равен
1)1(
1
)1(
)!1(
))...(1(
)(
++−
+
+
+
−
−
=
nn
n
xx
n
n
xR
α
θ
α
α
α
.
В частном случае, когда
α=n - целое число, R
n+1
(x)=0 и мы получим формулу
бинома Ньютона
....
!2
)1(
!1
)(
èëè
...
!2
)1(
!1
11)(
...
!2
)1(
!1
1)1(
221
2
2
nnnnn
n
n
n
nn
nn
xxa
nn
xa
n
axa
a
x
a
xnn
a
xn
a
a
x
axa
èxx
nn
x
n
x
++
−
++=+
++
−
+
+=
+=+
++
−
++=+
−−
Итак, общий случай бинома Ньютона является частным случаем формулы
Маклорена.
5.14.8.3. Приложения формулы Маклорена Приближенное вычисление числа е
n
n
def
n
e
+≡
∞→
1
1lim . Ранее были установлены оценки 2 ≤е<3. Положим в формуле
Маклорена для e
x
, х=1 и r=1, получим
)1(
!
1
...
!1
1
1
1+
++++=
n
R
n
e , где
)!1(
3
)!1(
)1(
1
+
<
+
≤
+
nn
e
R
n
.
Выбирая номер n достаточно большим, получим приближенное значение e с
любой наперед заданной точностью.
5.14.8.4. Вычисление пределов с помощью формулы Маклорена
Из полученных нами ранее разложений по формуле Маклорена элементарных
функций легко следуют более грубые разложения (с остаточным членом в форме
Пеано).

).(0
!
)1)...(1(
...
!2
)1(
!1
1)1(
),(0)1(...
432
)1ln(
),(0
)!2(
)1(...
!4!2
1cos
),(0
)!12(
)1(...
!5!3
sin
),(0
!
...
!2
1
2
1
432
12
242
22
1253
2
nn
n
n
n
n
n
n
n
n
n
n
n
x
xx
n
n
xxx
x
n
xxxx
xx
x
n
xxx
x
x
n
xxx
xx
x
n
xx
xe
+
+−−
++
−
++=+
+−++−+−=+
+−+−+−=
+
+
−+++−=
+++++=
−
+
+
+
αααααα
α
Эти разложения могут быть использованы при вычислении пределов функций при
x
→0.
Пример. Вычислить
)sin1(
lim
33
sin
0
xx
ee
tgxx
x
+
−
→
.
Так как в знаменателе старшая степень x - третья, то в числителе нужно
учитывать степени, не выше третьей.
Получим разложения функций, входящих в числитель, до членов с x
3
.
),(0
!3!2
1
3
32
z
zz
ze
z
++++=
[
3
32
sin
)(sin0
!3
)(sin
!2
)(sin
sin1 x
xx
xe
x
++++=
]
. (1)
Так как
1
sin
lim
0
=
→
x
x
x
, 0[(sinx)
3
]=0(x
3
), далее,
)(0
!3
sin
4
3
x
x
xx +−= .
Подставляя это разложение в (1) будем иметь
)(0
!3
))(0
!3
(
!2
))(0
!3
(
))(0
!3
(1
3
34
3
24
3
4
3
sin
x
x
x
xx
x
x
x
x
xe
x
+
+−
+
+−
++−+= .
Раскрывая скобки и учитывая, что x
k
⋅0(x
m
)=0(x
m+k
)=0(x
m
), получим
).(0
2
1
1
),(0
6
1
2
1
)
6
1
(1
32sin
3323sin
xxxe
xxxxxe
x
x
+++=
+++−+=
Получим теперь разложение tgx
=
++−−++−=
=+−⋅+−==
−
)(0))(0
2
)(1(1))(0
6
(
))(0
2
1())(0
6
(
cos
sin
33
2
3
3
13
2
3
3
xx
x
x
x
x
x
x
x
x
x
x
x
tgx
Здесь использовано разложение (1+z)
-1
=1-z+0(z)

).(
2
1
2
1
1)(0
6
1
2
1
)
3
(1
)(0
3
)(0
26
))(0
2
1))((0
6
(
332332
3
3
3
3
33
3
2
3
3
xxxxxxx
x
xe
x
x
xx
xx
xx
x
x
x
x
tgx
++++=+++++=
++=++−=+++−=
Подставляя в заданную функцию полученные разложения, будем иметь
.
2
1
)sin1(
)(0
2
1
lim
)sin1(
))(0
2
1
2
1
1()(0
2
1
1
lim
)sin1(
lim
33
33
0
33
33232
0
33
sin
0
−=
+
+−
=
=
+
++++−+++
=
+
−
→
→→
xx
xx
xx
xxxxxxx
xx
ee
x
x
tgxx
x
В этом примере использование правила Лопиталя было бы затруднительным, в то
время как применение формулы Маклорена опиралось только на известные
разложения элементарных функций.
5.15. Исследование поведения функций с помощью производных
5.15.1. Условие постоянства функций
Теорема 1.
Пусть функция f(x) определена, дифференцируема на интервале Х, и
на Х. Тогда функция f(x) является постоянной на Х.
()
0=
′
xf
Доказательство. Пусть x
0
- некоторая фиксированная точка из Х и х-любая
другая точка из Х. Для сегмента [x
0
, x] (или [x, x
0
]) удовлетворены все условия
теоремы Лагранжа, следовательно, между точками х
0
и х найдется точка ξ, такая
что
() ( ) ()
(
)
.
00
xxfxfxf −
′
=−
ξ
Так как f(ξ)=0, то для
(
)(
0
xfxfXx
)
=
∈
∀
, т.е. значение
функции f(x) в любой точке х
∈Х равно ее значению в фиксированной точке х
0
,
т.е. постоянна всюду в Х.
Замечание. Геометрический смысл теоремы: если касательная в каждой точке
некоторого участка графика функции y=f(x) параллельна оси ОХ, то этот участок
есть отрезок прямой, параллельный оси ОХ.
y
y=f(x)
x
0 a b
5.15.2. Признак монотонности функции
Теорема. (Достаточное условие возрастания (убывания) функции на интервале
Х).
Пусть функция f(x)
1) определена на интервале Х;
2) имеет на Х конечную производную
(
)
xf
′
;
3) >0 ( <0) на Х.
()
xf
′
()
xf
′
Тогда f(x) является возрастающей (убывающей) на интервале Х.
Доказательство. Рассмотрим случай, когда
(
)
xf
′
<0 на Х. Возьмем любые два
значения х
1
и х
2
из Х такие, что х
1
< х
2
, тогда на сегменте [х
1
, х
2
] f(x)
удовлетворяет всем условиям теоремы Лагранжа, поэтому справедливо равенство
() () ()( )
,
1212
xxfxfxf −
′
=−
ξ
где ξ- некоторая точка из (х
1
, х
2
): х
1
<ξ< х
2
. Так как х
2
> х
1
,
и
() ( )
(
)
12
xf òî,0 xff <<
′
ξ
, что означает убывание функции на множестве Х.
Для случаев
(
)
xf
′
>0 на Х доказательство проводится аналогично.
Замечание 1. Положительность (отрицательность) производной
на Х не
является необходимым условием возрастания (убывания) функции f(x), т.е. если
на некотором участке функция возрастает (убывает), то отсюда не следует,
вообще говоря, что на этом участке производная этой функции всюду
положительна (отрицательна).
()
xf
′
y
y=x
3
x
Рис.1
Например, для возрастающей на всей числовой оси функции
производная в
точке х=0 обращается в
3
xy =
03:0
0
2
0
==
′
== xx
xy (рис.1).
Замечание. Геометрическая интерпретация теоремы: поскольку производная
функции представляет собой угловой коэффициент касательной к графику
функции, то знак производной показывает острый (если
(
)
xf
′
>0) или тупой (если
<0) угол с положительным направлением оси ОХ составляет касательная к
f(x). В соответствии с этим, кривая идет вверх (функция f(x) возрастает) или вниз
(функция f(x) убывает). В отдельных точках при этом касательная может быть
параллельной оси ОХ, что соответствует обращению в нуль производной
функции f(x) (рис.2,3)
()
xf
′
y y
.
Рис.2 Рис.3
5.15.3. Экстремум дифференцируемой функции
Необходимое условие экстремума функции в точке : если f(x)
дифференцируема в точке С и имеет в этой точке локальный экстремум, то
Таким образом, экстремум дифференцируемой функции следует искать
лишь в тех точках, где производная равна нулю. Такие точки называются
()
.0=
′
cf
стационарными. Заметим, что если точка стационарна, то отсюда, вообще
говоря, не следует, что в этой точке функция достигает экстремума, т.е. указанное
необходимое условие экстремума функции не является достаточным (для f(x)=x
3
в
точке х=0 экстремума нет, однако
(
)
030
0
2
==
′
=x
xf ).
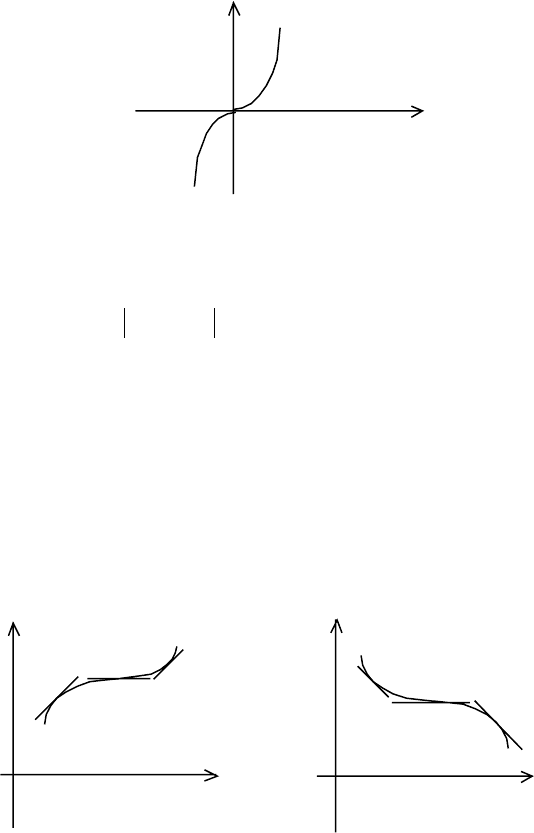
Теорема 1. (первое достаточное условие экстремума дифференцируемой
функции).
Пусть функция y=f(x).
1) дифференцируема всюду в некоторой окрестности т. С.
2) т. С - стационарная, т.е.
0)(
=
′
cf , тогда а) если существует окрестность, в
которой производная
положительна (отрицательна) слева от точки С и
отрицательна (положительна) справа от точки С, то функция f(x) имеет в т. С
локальный максимум (минимум) (рис. 1,2);
)(›f
′
б) если же производная имеет один и тот же знак слева и справа от точки С,
то экстремума в т. С нет (рис.3,4).
)(xf
′
y y y y
макс.
экстр. нет экстр.нет
′
>
fx() 0
′
<
fx() 0
′
<
fx() 0
′
>
fx() 0
′
>
fx() 0
′
<
fx() 0
мин.
′
>
fx() 0
′
<
fx() 0
c x с x c x c x
Рис.1 Рис.2 Рис.3 Рис.4
Доказательство. Докажем теорему для точки максимума. Пусть
положительна в окрестности слева от точки С и отрицательна справа от точки С.
)(›f
′
() ()
CxCxxf >∀
<
′
<∀>
′
0xf è 0
. Обозначим через х
0
-любое значение аргумента из
окрестности х
0
>С. На сегменте [C,x
0
] функция f(x) дифференцируема,
следовательно, и непрерывна, поэтому по теореме Лагранжа
()
(
)
(
)
(
)
00
xCfxfCf
−
′
=
−
ξ
, (1)
где
ξ - некоторое значение аргумента между точками С и х
0
.
Аналогично рассматривается случай х
0
<C.
При х
0
>С
()
0,0
0
<−
<
′
xCf
ξ
, поэтому f(C)>f(x
0
). Это и означает, что в точке С
f(x) имеет локальный максимум.
Теорема 2. (второе достаточное условие экстремума).
Пусть функция y=f(x)
1) имеет производную всюду в некоторой окрестности т. С;
2) т. С - стационарная: f(x)=0;
3) имеет конечную вторую производную в т. С.
Тогда, если
(
)
0<
′
′
Cf
, то в т. х=С f(x) имеет локальный максимум, если же
то в точке х= С f(x) имеет локальный минимум.
()
,0>
′′
Cf
Замечание. Теорема 2 не дает ответ о наличии экстремума в том случае, когда
или не существует в т. х= С. В этом случае поведение функции в т. С
следует изучить с помощью первого достаточного условия экстремума.
()
0=
′′
Cf
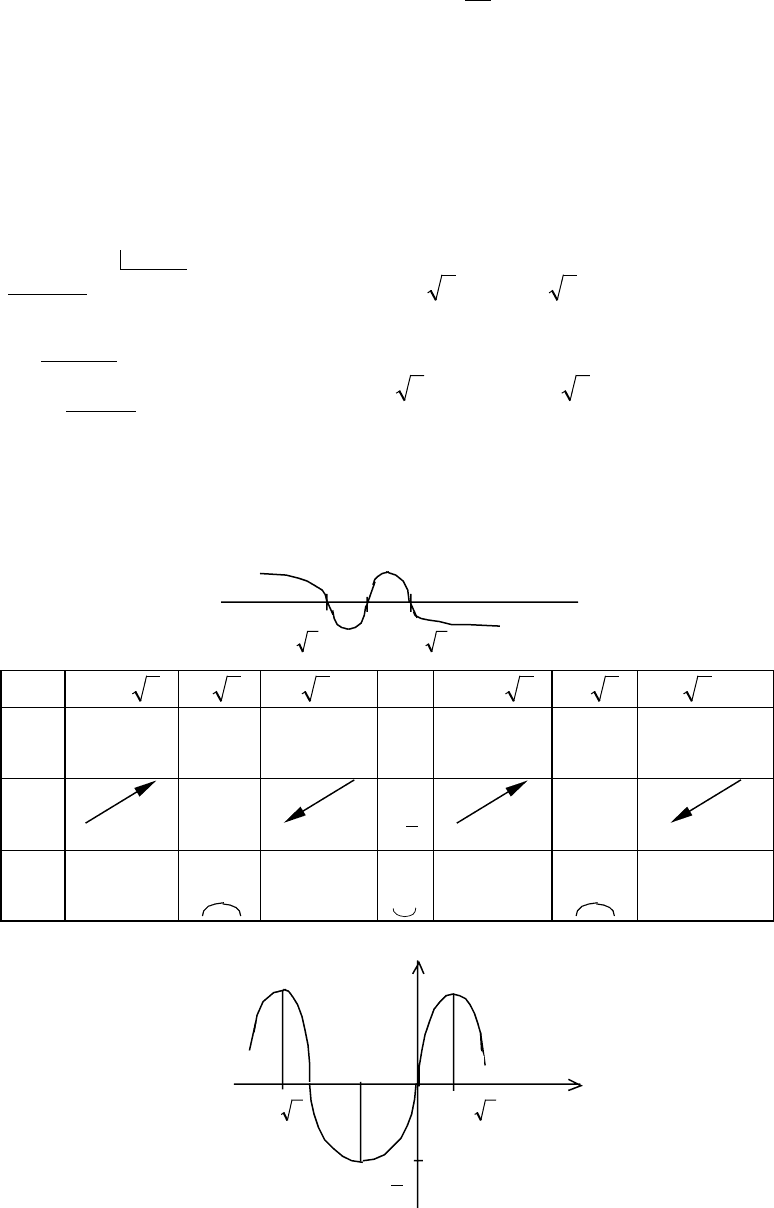
Пример. Найти экстремум функции .
4
4
3
4
2
x
x
xxy −−+=
042 =−− x
Вычислим производную:
Производная определена и дифференцируема на всей числовой
оси. Найдем стационарные точки, решив уравнение
. Рассматриваем делители
свободного члена : ±1; ±2. Отсюда получаем корень х
.234
32
xxxy +−−=
′
()
3x-4 .0
32
−=
′
xxy 3 xèëè 02
23
+=+ xx
1
=-1.
Деля
на х+1,получим: 423
23
−−+ xxx
(
)
(
)
421423
223
−++=−−+ xxxxxx
x
3
+3x
2
-2x-4 x+1
-
x
3
+x
2
x
2
+2x-4
2x
2
-2x-4
-
2x
2
+2x
-4x-4
-
-4x-4
0
Решая квадратное уравнение x
2
+2x-4=0,
получим x
2
=-1+ 5 , x
3
=-1- 5
Итак, имеем:
)51)(1)(51()( −++++−=
′
xxxxy
Определим участки возрастания и убывания функции и исследуем функцию на
экстремум.
+ +
— —
−−15
-1
−−15
x
(-
∞,-1- 5 ) -1- 5 (-1- 5 ,-1)
-1
(-∞,-1+ 5 )-1+ 5 (-1+ 5 ,+∞)
y
′
+
0
+
0
—
0
+
y
4
4
9
−
4
Рис.
лок.
макс.
лок.
мин.
лок.
макс.
y
−−15
-1
−+15
x
−
9
4
Пример 2. Найти экстремум функции . Находим производную
. Стационарные точки х
43
23
−−= xxy
(
2363
2
−=−=
′
xxxxy
()
1666 −=−=
′′
xxy
)
1
=0 и х
2
=2. Вычислим
. Так как
()
(
)
062y è > 060
=
′
′
<
−
=
′′
y , то в т. х=0 - локальный
максимум, а в точке х=2- локальный минимум.
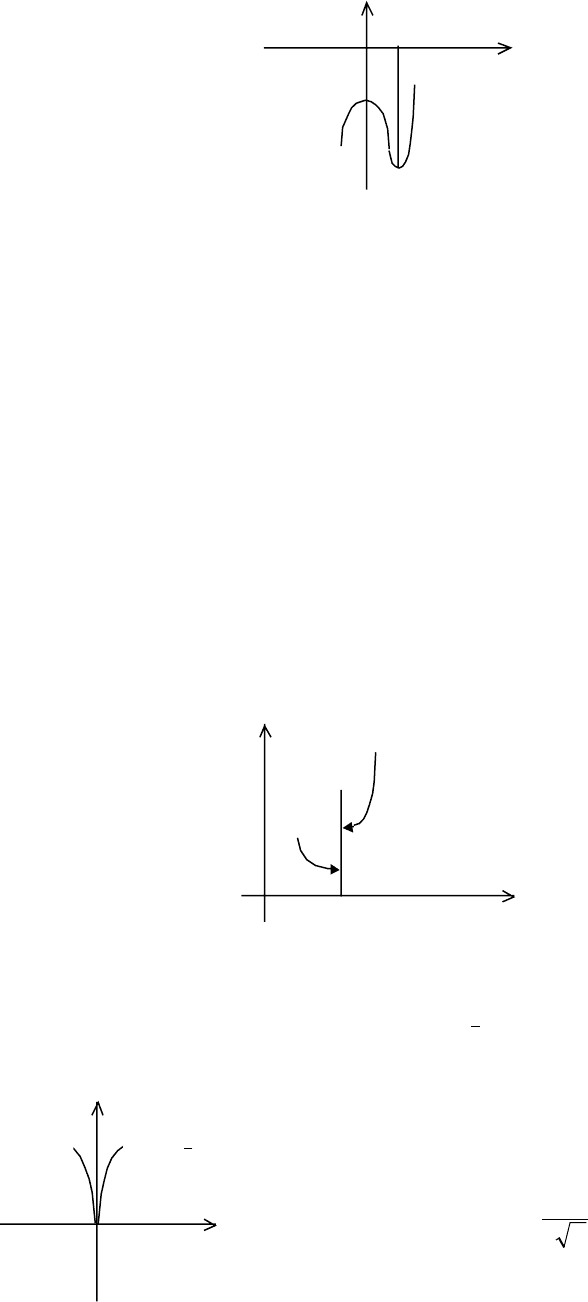
y
2 x
-4
-8
5.15.4. Экстремум функции, недифференцируемой в данной точке
Теорема. Пусть функция у=f(x).
1) дифференцируема всюду в некоторой окрестности точки С, за исключением,
быть может, самой точки С;
2) непрерывна в точке С.
Тогда, если существует окрестность точки С, в пределах которой
производная
положительна (отрицательна) слева от точки С и отрицательна
(положительна) справа от точки С, то функция f(x) имеет в точке С локальный
максимум (минимум). Если же производная
()
xf
′
(
)
xf
′
имеет один и тот же знак слева и
справа от точки С, то экстремума в точке С нет.
Замечание. Требование 2) непрерывности функции в точке С существенно, ибо
отсутствие этого требования может привести к функциям (см. рис. 1), не
имеющим экстремума в т. С.
y
•
c x
Рис.1.
Пример. Найти точки экстремума функции
3
2
xy = .
y
yx=
2
3
0 x
Рис.2
Эта функция непрерывна на всей
бесконечной прямой (см.рис.2),
дифференцируема всюду на этой прямой, за
исключением точки х=0. Производная
функции при
3
x3
2
=y 0
′
≠x
0 0
. В точке х=0 эта
производная имеет разрыв 2-го рода.
Поскольку при
<
′
<
yx , а при ,
то, следовательно, в силу теоремы в точке
х=0 функция имеет минимум.
0 0 >
′
> yx
Замечание. Сформулируем общую схему нахождения точек экстремума.
Пусть функция f(x).
1) непрерывна на множестве Х;
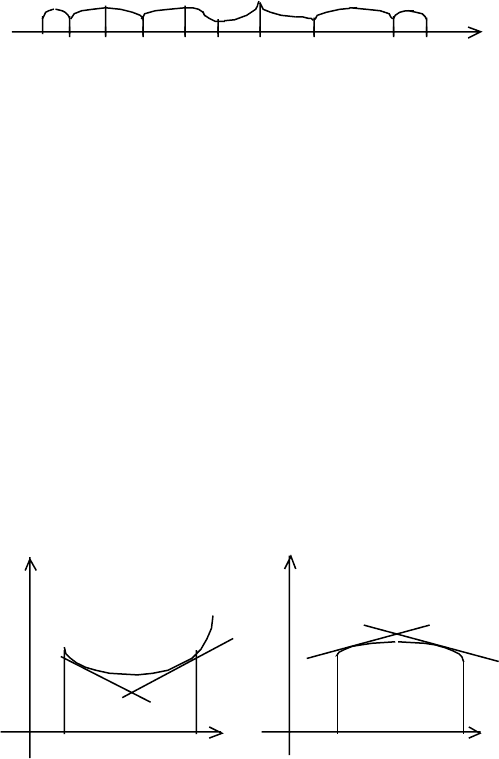
2) производная существует и непрерывна внутри Х всюду, кроме быть
может, конечного числа точек;
()
xf
′
3) пусть производная
обращается в 0 внутри Х лишь, может быть, для
конечного числа точек.
()
xf
′
Обозначим через х
1
,х
2
,...х
n
точки, в которых производная не существует или
равна нулю, а через a и b - концы Х (a и b могут быть и бесконечными).
a x
1
x
2
x
3
x
i
x
i+1
x
i+2
b x
На каждом интервале (а
1
х
1
),(х
1
х
2
),...(x
i-1
x
i
),...)(x
n
b) производная в силу
условий 1)-3) сохраняет постоянный знак. Поэтому вопрос о наличии экстремума
в каждой точке х
()
xf
′
i
может быть решен при помощи рассмотренных достаточных
условий.
5.15.5. Направление выпуклости графика функции
Пусть функция f(x) дифференцируема в любой точке интервала (а,b), тогда
через любую точку М(х, f(x)) этого графика функции можно провести
касательную к графику функции f(x), причем эта касательная не параллельна оси
OY, т.к. ее угловой коэффициент конечен, ибо равен производной
.
()
xf
′
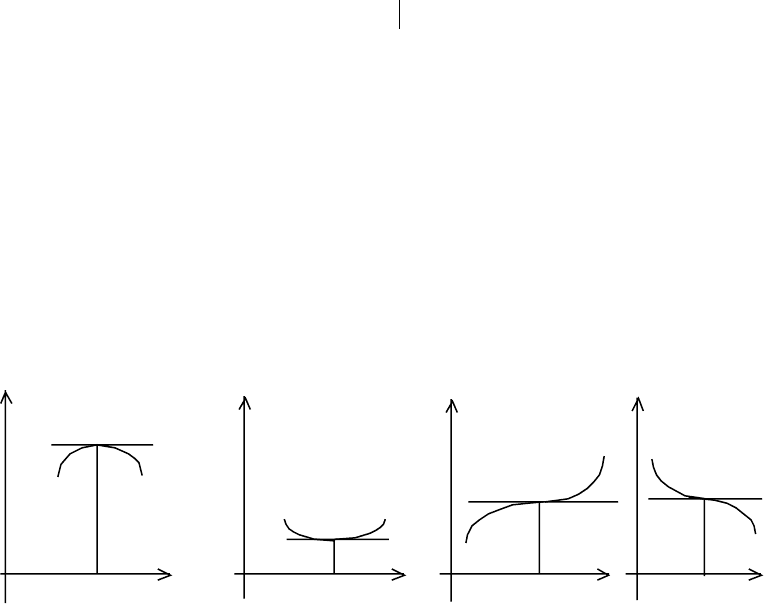
Определение. Говорят, что график функции f(x) имеет на (a,b) выпуклость
направленную вниз (вверх), если график этой функции в пределах (a,b) лежит не
ниже (см. рис 1,2) (не выше) любой своей касательной.
y y
a b x a b x
Рис.1 Рис.2
Теорема 1. Пусть функция y=f(x) имеет на интервале (a,b) конечную вторую
производную, тогда если
()
(
)
(
)
(
)
(
)
baxxfbaxxf , 0 , 0
∈
∀
≤
′
′
∈
∀
≥
′′
, то график функции
y=f(x) имеет на (a,b) выпуклость, направленную вниз (вверх).
Замечание. Если
(
)()
(
)
xf=y òî,,0 baxxf ∈∀=
′
′
- линейная функция, т.е. ее графиком
является прямая линия. В этом случае направление выпуклости можно считать
произвольным.
Пример.
() ()
(
)
(
)(
1666 ;2363 ;43
223
−=−=
′′
−=−=
′
−−= xxxfxxxxxfxxxf
)
Таким образом, при
, а при
()
0 1 >
′′
> xfx
(
)
0xf 1< x
<
′
′
и, следовательно, при −∞<
х
<1 график функции имеет выпуклость вверх, а при 1<х< ∞ -вниз (см. рис.4).
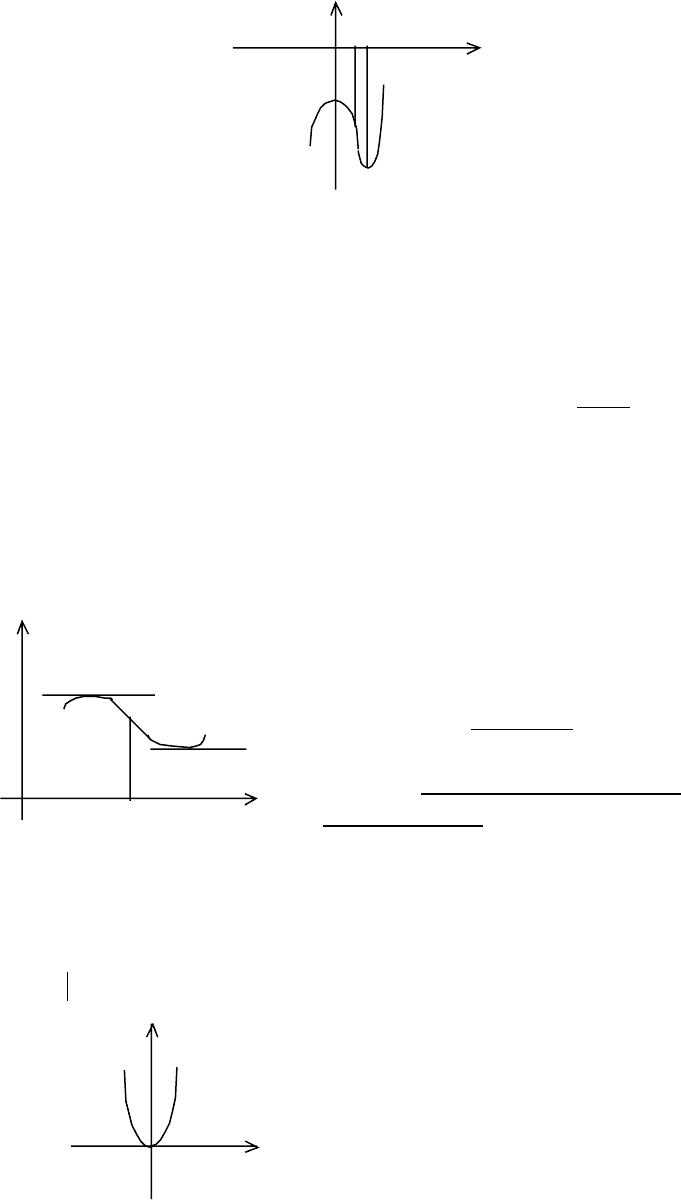
y
1 2 x
-4
-6
-8
Рис.4
5.15.6. Точки перегиба графика функции
Предположим, что график функции y=f(x) имеет определенное направление
выпуклости на каждом из интервалов (а,с) и (с,b), где числа а,b,c
связаны
неравенствами a<c<b. Предположим, что к графику функции y=f(x) в точке
М(с,f(c)) cуществует касательная не параллельная оси OY, тогда точка М(с,f(c))
графика функции y=f(x) называется точкой перегиба этого графика, если
существует такая окрестность точки С оси абсцисс, в пределах которой график
функции y=f(x) слева и справа от точки С имеет разные направления выпуклости
(см.рис.1)
y
•
M
c x
Рис.1
Теорема 1. (необходимое условие
существования точки перегиба).
Пусть график функции
y=f(x) имеет перегиб
в точке
М(с,f(c)) и функция y=f(x) имеет в
точке С непрерывную вторую
производную f
2
(с)=0.
Замечание1. Равенство нулю второй производной не является достаточным
условием перегиба. Например, для функции y=x
4
в точке (0,0) нет перегиба,
однако
()
0120
0
2
==
′′
=x
xy . (см. рис. 2)
y
0 x
Замечание 2. Все точки
перегиба дважды нпрерывно
дифференцируемой функции
находятся среди точек, в
которых вторая производная
равна нулю.
5.15.7. Теоремы о достаточных условиях перегиба графика функции
Теорема 1. (первое достаточное условие перегиба).
Пусть функция f(x)
1) имеет вторую производную в некоторой окрестности точки С;
2)
, тогда, если существует окрестность, в пределах которой вторая
производная
имеет разные знаки слева и справа от точки C, то график этой
функции имеет перегиб в точке М(с,f(с)).
()
0=
′′
cf
()
xf
′′
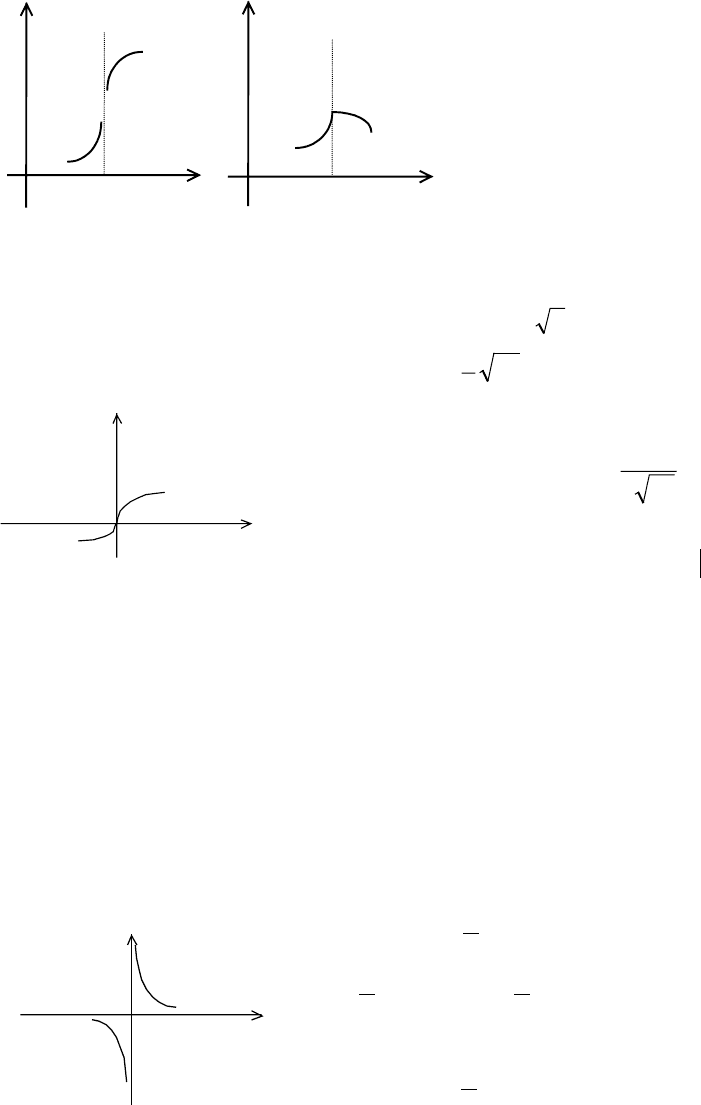
Замечание 1. Сформулируем обобщение теоремы 1. При определении точки
перегиба будем считать, что касательная к графику функции в рассматриваемой
точке может быть параллельной оси 0y (т.е.
(
)
±
∞
=
′
cf ).
Пусть функция f(x): 1) имеет конечную вторую производную всюду в некоторой
окрестности точки С, за исключением, быть может, самой точки С; 2) функция
f(x) непрерывна в точке С; 3) график функции имеет касательную в точке
М(с,f(с))(может быть и параллельно оси 0y). Тогда, если существует окрестность
точки С, в пределах которой
имеет разные знаки слева и справа от точки С,
то график функции y=f(x) имеет перегиб в точке М(с,f(с)).
()
xf
′′
Замечание 2.
y y
M
M
C x C x
Рис. 1 Рис. 2
Пункт 2 в условии
теоремы исключает
случай, приведенный на
рис. 1, а пункт 3 - на рис.
2 (слева от точки С
график функции касается
прямой х=С в точке М, а
справа касания нет)
Пример. Найти точки перегиба графика функции
3
xy = .
y
0 x
Рис. 3
Так как
()
3
2
3
1
xxy =
′
, то в точке х=0
+
∞
=
′
y и график функции касается в
точке (0,0) оси ОУ.
()
35
9
2
x
xy −=
′′
и
поэтому
(
)
ïðè 0> 0< x
′
′
xy
0> x
и
ïðè 0<y
′
′
, а в точке х=0
()
∞=
′′
=0x
xy .
Отсюда следует, что точка (0,0) является точкой перегиба; слева от этой точки
график функции имеет выпуклость вниз, а справа вверх.
5.15.8. Асимптоты графика функции
Определение 1. Прямая х=а называется вертикальной асимптотой графика
функции y=f(x), если хотя бы одно из предельных значений
()
(
)
xfxf
ax 0-ax0
lim è lim
→+→
равно
+∞ или −∞.
y
x
Рис. 1
Пример.
x
y
1
=
. Так как
+∞=−∞=
→−→
xx
x
1
lim è
1
lim
0+0x00
, то прямая х=0
- вертикальная асимптота графика
функции
x
y
1
=
. (см. рис. 1)
