Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.

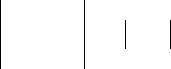
1)
(по определению).
0dx)x(f
a
a
=
∫
2)
(по определению, при a<b).
∫∫
−=
a
b
b
a
dx)x(fdx)x(f
3)
(с = const).
∫∫
=
b
a
b
a
dx)x(fcdx)x(cf
4)
[]
∫∫∫
±=±
b
a
b
a
b
a
dx)x(gdx)x(fdx)x(g)x(f
5)
для произвольных с, при условии интегрируемости
функции f(x).
∫∫∫
+=
b
c
c
a
b
a
dx)x(fdx)x(fdx)x(f
6)
если f(x) ≥0 ∀x ∈ [a,b].
,0dx)x(f
b
a
≥
∫
7) Если функция f(x) ∈ c[a,b], то свойство 6) можно уточнить при f(x) ≡ 0.
8)
если f(x) ≥g(x) ∀x ∈ [a,b].
∫∫
≥
b
a
b
a
dx)x(gdx)x(f
9)
∫∫
≤
b
a
b
a
dx)x(fdx)x(f .
10)
,dx)x(gMdx)x(g)x(fdx)x(gm
b
a
b
a
b
a
∫∫∫
≤≤
если
g(x) ≥0 ∀x ∈ [a,b], )x(fsupM
]b,a[
=
, m )x(finf
]b,a[
=
.
7.6. Первая и вторая формулы среднего значения
Докажем формулу, которая называется первой формулой среднего значения.
Пусть функции f(x) и g(x) интегрируемы на сегменте [a,b], и функция g(x) не
меняет знака на этом сегменте. Если
M )x(fsup
]b,a[
=
, m )x(finf
]b,a[
=
, то существует число
µ, удовлетворяющее неравенствам m ≤ µ ≤ M, такое, что справедлива формула
∫∫
=
b
a
b
a
dx)x(gdx)x(g)x(f
µ
. (1)
Если, в частности, f(x) непрерывна на сегменте [a,b], то ∃ξ∈[a,b], что будет
выполняться равенство
∫∫
=
b
a
b
a
dx)x(g)(fdx)x(g)x(f
ξ
. (2)
Замечание. Формула (1) и (2) называется первой формулой среднего значения.
Доказательство. Будем предполагать, что g(x)
≥0 (в случае g(x) ≤ 0 рассуждения
аналогичные).
а) Если
, то в силу свойства 10 определенного интеграла
(см. тему 5)
0dx)x(g
b
a
=
∫
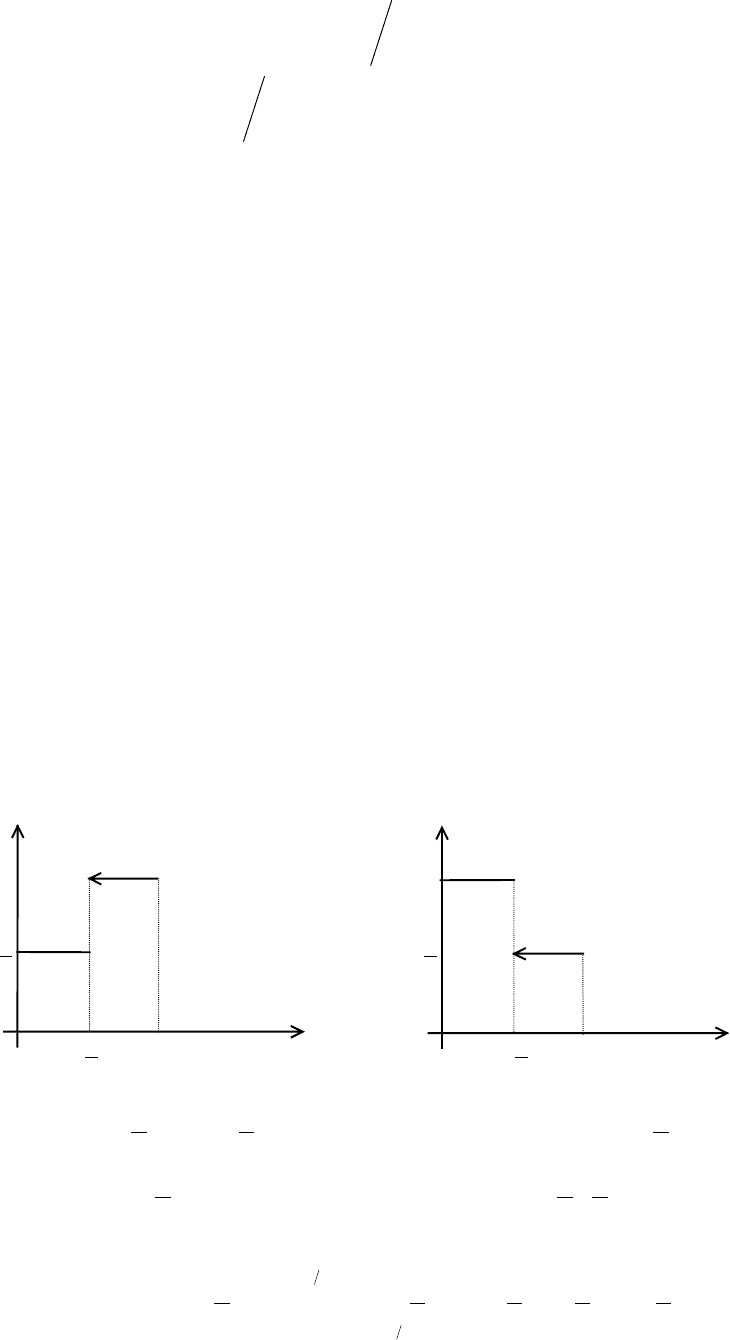
0dx)x(g)x(f
b
a
=
∫
,
и тогда в качестве µ можно взять любое число.
в) Пусть
, тогда из (10)
0dx)x(g
b
a
>
∫
Mdx)x(gdx)x(g)x(fm
b
a
b
a
≤≤
∫∫
.
Обозначая через
∫∫
=
b
a
b
a
dx)x(gdx)x(g)x(f
µ
, будем иметь формулу (1).
Формула (1) доказана.
Для доказательства формулы (2) нужно показать, что в случае непрерывной
функции f(x) найдется такая точка
ξ∈[a,b], что f(ξ)=µ в формуле (1). Однако это
вытекает из того, что непрерывная на сегменте [a,b] функция достигает на этом
сегменте как своих точных граней M и m, так и любого промежуточного между
ними значения
µ (m ≤ µ ≤ M).
Следствие. В частном случае, когда g(x)
≡1, формула (1) принимает вид:
)ab(dx)x(f
b
a
−⋅=
∫
µ
,
а (в предположении непрерывности функции f(x) на сегменте [a,b]) формула (2)
превращается в
)ab()(fdx)x(f
b
a
−⋅=
∫
ξ
Замечание. Если f(x) не является непрерывной, то формула (3), вообще говоря,
неверна.
Пример.
f(x) g(x)
1 1
1
2
1
2
1
2
1 x
1
2
1 x
≤<
≤≤
=
1x
2
1
,1
2
1
x0 ,
2
1
)x(f
≤<
≤≤
=
1x
2
1
,
2
1
2
1
x0 ,1
)x(g
.
3
2
;
4
3
2
1
dx
2
1
dx1dx
2
1
dx)x(g)x(f
1
21
21
0
1
0
b
a
=⋅=⇒
⋅+⋅==
∫∫∫∫
µµµ

и для ∀ξ∈[0,1] f(ξ)≠µ.
Сформулируем без доказательства теорему, позволяющую получить
формулу, известную под названием второй формулы среднего значения, или
формулы Бонне. Эта формула будет неоднократно использоваться в разных
разделах математического анализа, в частности, в разделе “Несобственные
интегралы”.
Теорема. Если на сегменте [a,b] функция g(х) монотонна, а f(x) интегрируема, то
на этом сегменте существует такая точка
ξ, что
∫∫∫
+=
b
a
b
a
dx)x(f)b(gdx)x(f)a(gdx)x(g)x(f
ξ
ξ
- вторая формула среднего значения или формула Бонне.
7.7. Интеграл с переменным верхним пределом
Одним из важных понятий для непрерывных и интегрируемых на сегменте
[a,b] функций является понятие интеграла с переменным верхним пределом,
используя которое, можно получить основную формулу интегрального
исчисления - формулу Ньютона-Лейбница.
Определение. Пусть функция f(x) интегрируема на любом сегменте [
α,β]∈(a,b) и
пусть c - некоторая фиксированная точка, принадлежащая интервалу (a,b), тогда,
каково бы ни было число х
∈( a,b), функция f(x) интегрируема на [c,x], и на
интервале (a,b) определена функция
, которая называется интегралом
с переменным верхним пределом.
∫
=
x
c
dt)t(f)x(F
Теорема. Любая непрерывная на интервале (a,b) функция f(x) имеет на этом
интервале первообразную. Одной из первообразных является функция
, где с - любая фиксированная точка интервала (a,b).
∫
=
x
c
dt)t(f)x(F
Достаточно доказать, что для
)x(f
x
)x(F)xx(F
lim)b,a(x
0x
=
∆
−
∆
+
∃∈∀
→∆
(∆х берем
таким, чтобы (х+
∆х)∈(a,b)). Рассмотрим разность
,x)(fdt)t(f
dt)t(fdt)t(fdt)t(fdt)t(fdt)t(f)x(F)xx(F
xx
x
x
c
xx
x
x
c
x
c
xx
c
∆=
=−+=−=−∆+
∫
∫∫∫∫∫
∆+
∆+∆+
ξ
где
ξ - некоторое число, заключенное между х и х+∆х (Здесь было использовано
свойство 6 определенного интеграла и первая формула среднего значения для
непрерывной на сегменте функции (см. темы 5 и 6 данного методического
пособия)).
Так как f(x) непрерывна в точке х, то при
∆х→0 f(ξ)→f(x), и поэтому
)x(f
x
)x(F)xx(F
lim
0x
=
∆
−∆+
→∆
.

Замечание 1. Аналогично доказывается теорема для непрерывной на сегменте
[a,b] функции f(x). В этом случае в качестве с можно взять точку а и
F
.
∫
=
x
a
dt)t(f)x(
Замечание 2. Мы показали, что
)x(fdt)t(f
dx
d
x
c
=
∫
.
Замечание 3. Если f(x) интегрируема на любом сегменте, содержащемся в
интервале (a,b), то интеграл с переменным верхним пределом представляет собой
непрерывную функцию на интервале (a,b) от верхнего предела. В самом деле
,xdt)t(fdt)t(f)x(F)xx(FF
x
c
xx
c
∆⋅=−=−∆+=∆
∫∫
∆+
µ
где m
≤ µ ≤ M
=
=
)x(finfm
)x(fsupM
]b,a[
]b,a[
Отсюда
0)x(limFlim
0x0x
=
∆⋅=∆
→∆→∆
µ
, и в силу разностной формы условия
непрерывности F(x) есть непрерывная на интервале (a,b) функция.
7.8. Основная формула интегрального исчисления или формула Ньютона-
Лейбница
В разделе “Неопределенный интеграл” курса математического анализа было
показано, что любые две первообразные функции f(x) на сегменте [a,b]
отличаются лишь на константу (см., например, [9] стр. 26). В предыдущей теме
(№7) данного пособия была доказана теорема, что интеграл с переменным
верхним пределом F(x)=
является одной из первообразных функции f(x) на
сегменте [a,b] (с,х∈[a,b]), поэтому любая первообразная ϕ(х) непрерывной на
сегменте [a,b] функции f(x) может быть представлена в виде
(тема
№7, замечание 1), где с - произвольная постоянная. Используя свойство 1
определенного интеграла (см. тему 5), имеем
. Очевидно также,
что при х=b
, откуда .
∫
x
c
dt)t(f
(fc
b
a
=+
∫
cdt)t(f)x(
x
a
+=
∫
ϕ
c=
c
cdt)t(f)a(
a
a
+=
∫
ϕ
)b(dx)x(f
b
a
−=
∫
ϕ
cdx)xdt)t(f)b(
b
a
+=
∫
ϕ
Подставляя вместо с Ф(а) в последнее равенство, получим формулу
)a()b(dx)x(f
b
a
ϕϕ
−=
∫
.
Для удобства записи разность
ϕ (b)- ϕ(а) записывают в форме
b
a
)x(
ϕ
, и
b
a
b
a
)x(dx)x(f
ϕ
=
∫
- основная формула интегрального исчисления или формула
Ньютона-Лейбница.
Примеры:

1.
1243
1arctg3arctg
1
3
arctgx
x1
dx
3
1
2
πππ
=−=−==
+
∫
2.
()
111
2
1
02cos
2
2cos
2
1
0
2
x2cos
2
1
xdx2sin
2
0
=−−−=
⋅−⋅−=−=
∫
π
π
π
3.
6
0arcsin
2
1
arcsin
0
2
4
x
arcsin
x16
dx
2
0
2
π
=−==
−
∫
4.
()
2
3
41
2
1
6
sin
1
2
sin
1
2
1
6
2
xsin2
1
dx
xsin
xcos
22
2
2
6
2
=−−=
−−=−=
∫
ππ
π
π
π
π
7.9. Формулы замены переменной и интегрирования по частям в
определенном интеграле
Теорема. Пусть функция f(x) непрерывна на сегменте [a,b]. Сегмент [a,b] является
множеством значений некоторой функции x=g(t), определенной на сегменте
α ≤ t
≤ β, причем g(α)=a, g(β)=b.
Пусть также g'(t) непрерывна
∀t∈ [α,β]. Тогда справедлива формула:
- формула замены переменной под знаком определенного
интеграла.
∫∫
′
=
β
α
dt)t(g)]t(g[fdx)x(f
b
a
Доказательство. Пусть
ϕ (x) - некоторая первообразная функции f(x), т.е.
)x(f)x( =
ϕ
и (см. тему 8). Так как функции Ф(х) и x=g(t)
дифференцируемы на соответствующих сегментах, то сложная функция Ф[g(t)]
дифференцируема на сегменте [
α,β]. Применяя правило дифференцирования
сложной функции, получим
)a()b(dx)x(f
b
a
ϕϕ
−=
∫
[][
)t(g)t(g)t(g
d
]
t
d
′
⋅=
ϕϕ
,
где производная Ф' вычисляется по аргументу х:
[
]
)x()t(g
ϕ
ϕ
=
, где x=g(t). Так как
)x(')x('
ϕ
ϕ
= , то при x=g(t) получим
[
]
)]t(g[f)t(g'
=
ϕ
. Подставляя это значение
[
]
)t(g'
ϕ
в правую часть (1), получим
[][]
)t(g)t(gf)t(g
d
t
d
ϕ
′
=
, откуда следует, что ϕ[g(t)] на
сегменте [
α,β] является первообразной для функции
[
]
)t(g)
′
t(gf . Поэтому по
формуле Ньютона-Лейбница
[] [ ][
)(g)(gdt)t(g)t(gf
αϕβϕ
β
α
−=
′
∫
]
,
а так как g(
β)=b и g(α)=a, то окончательно получим
[]
() ()
abdt)t(g)t(gf
ϕϕ
β
α
−=
′
∫
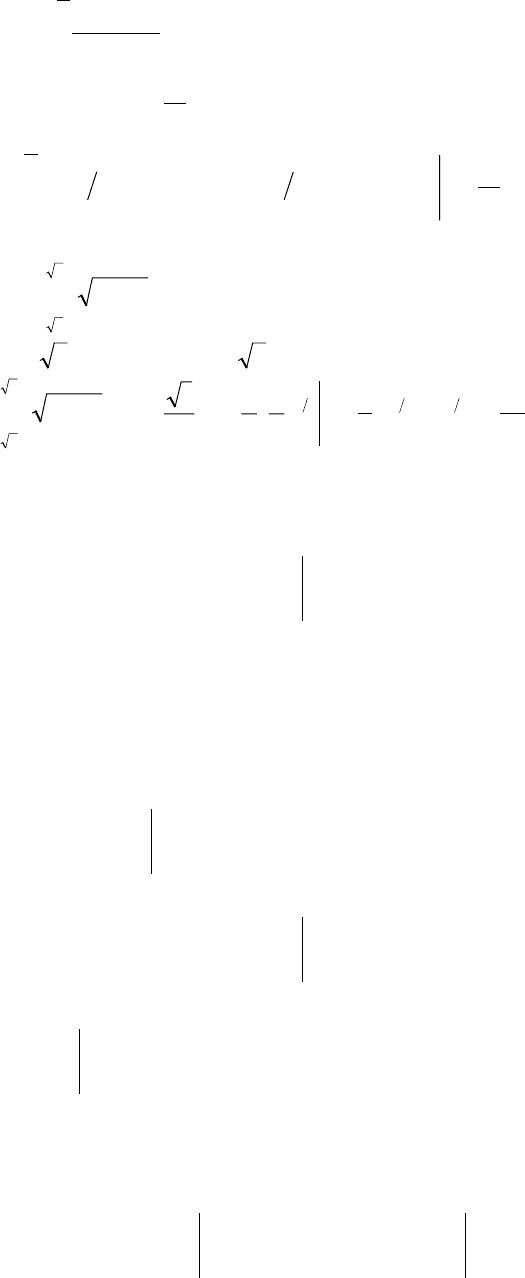
Пример 1. Рассмотрим
∫
Π
+
2
0
2
dx
xsin1
xcos
. Положим sinx=t, и, следовательно, dt=cosxdx;
так как t=0 при x=0 и t=1 при
2
x
Π
= , то
4
0
1
arctgt)t1(dtdx)xsin1(xcos
1
0
2
2
0
2
Π
==+=+
∫∫
Π
Пример 2. Вычислить
∫
+
8
3
2
dxx1x . Положим 1+х
2
=t, тогда dt=2xdx.
Поскольку t=4 при
3x = и t=9 при 8x = , то
()
3
19
49
3
1
4
9
t
3
2
2
1
dt
2
t
dxx1x
232323
9
4
8
3
2
=−=⋅==+
∫∫
Теорема. Если функции u(x) и v(x) на сегменте [a,b] имеют непрерывные
производные, то справедлива следующая формула
[]
∫∫
′
−=
′
b
a
b
a
dx)x(v)x(u
a
b
)x(v)x(udx)x(v)x(u
,
которая называется формулой интегрирования по частям для определенных
интегралов.
Доказательство. Поскольку
[]
)x(v)x(u)x(v)x(u)x(v)x(u
′
+
′
=
′
, то функция u(x)⋅v(x)
является первообразной для функции
[
]
)x(v)x(u)x(v)x(u
′
+
′
, откуда следует, что
[][]
a
b
)x(v)x(udx)x(v)x(u)x(v)x(u
b
a
=
′
+
′
∫
. Используя свойства определенного интеграла,
получим
[]
∫∫
′
−=
′
b
a
b
a
dx)x(v)x(u
a
b
)x(v)x(udx)x(v)x(u
.
Замечание. Так как
и dvdx)x(v =
′
dudx)x(u
=
′
, то полученная формула может быть
записана в виде
()
∫
−=
b
a
vdu
a
b
uv
∫
b
a
udv
.
Пример 1. Вычислить
. Полагая u=x, dv=sinxdx, получим du=dx, v = -
cosx, тогда
∫
π
0
xdxsinx
π
π
π
π
ππ
=+=−−−=
∫∫
0
xsindx)xcos(
0
xcosxxdxsinx
00
.
7.10. Спрямляемость и длина дуги плоской кривой
Пусть заданы функции
ϕ(t) и ψ(t), непрерывные на сегменте [α,β].
Множество {M} всех точек М, координаты х и у которых определяются
уравнениями
называется простой кривой, если различным
βα
ψ
ϕ
≤≤
=
=
t
)t(y
)t(x

значениям параметра t из сегмента [α,β] отвечают различные точки этого
множества.
y
A(
α
)
x
B(
β
)
Будем называть точки А и В,
отвечающие граничным значениям
α и β параметра t граничными
точками простой кривой. Простой
замкнутой кривой называется
кривая L, которая образуется
объединением двух простых кривых
L
1
и L
2
следующим образом:
1) граничные точки кривой L
1
, совпадают с граничными точками кривой L
2
; 2)
любые не граничные точки кривых L
1
и L
2
различны.
Определение. Пусть
ϕ(t) и ψ(t) непрерывны на {t}. Уравнения
=
=
)t(y
)t(x
ψ
ϕ
(1)
задают параметрически кривую L, если существует такая система сегментов
, разбивающих множество {t}, что для значений t из каждого данного
сегмента этой системы уравнения (1) определяют простую кривую. При этом
точки кривой L рассматриваются в определенном порядке в соответствии с
возрастанием параметра t, т.е. если M
[
{
i1i
t,t
−
]
}
1
соответствует значению параметра t
1
, а М
2
- t
2
, то M
1
считаются предшествующей М
2
, если t
1
<t
2
. Точки, отвечающие
различным значениям параметра, всегда считаются различными.
Пример. Рассмотрим кривую L, задаваемую параметрически уравнениями
=
=
tsiny
tcosx
(2)
0
≤ t ≤ 4π - это не простая кривая, но если взять систему сегментов [0, π], [π,2π],
[2
π,3π], [3π,4π], разбивающих [0,4π], то для значений t из каждого
указанного сегмента данной системы
уравнения (2) определяют простую
кривую (полуокружность). Кривая L
- дважды обходимая окружность.
Итак, пусть кривая L задается параметрическими уравнениями
.
Пусть Т - произвольное разбиение [
α,β] точками α
βα
ψ
ϕ
≤≤
=
=
t
)t(y
)t(x
0
=t
0
<t
1
<t
2
<...<t
n
= β.
Соответствующие точки кривой L обозначим через М
0
, М
1
, М
2
, ..., М
n
М
0
М
1
М
2
М
n
t
0
t
1
t
2
t
n
Ломаную M
0
M
1
M
2
...M
n
будем
называть ломаной, вписанной в
кривую L и отвечающей данному
разбиению Т сегмента [
α,β]. Длина
l
i
звена M
i-1
M
i
этой ломаной равна
()()
[][ ]
2
1ii
2
1ii
2
1ii
2
1ii
)t()t()t()t(
yyxx
−−
−−
−+−=
=−+−
ψψϕϕ
Длина
)T(l всей этой ломаной равна
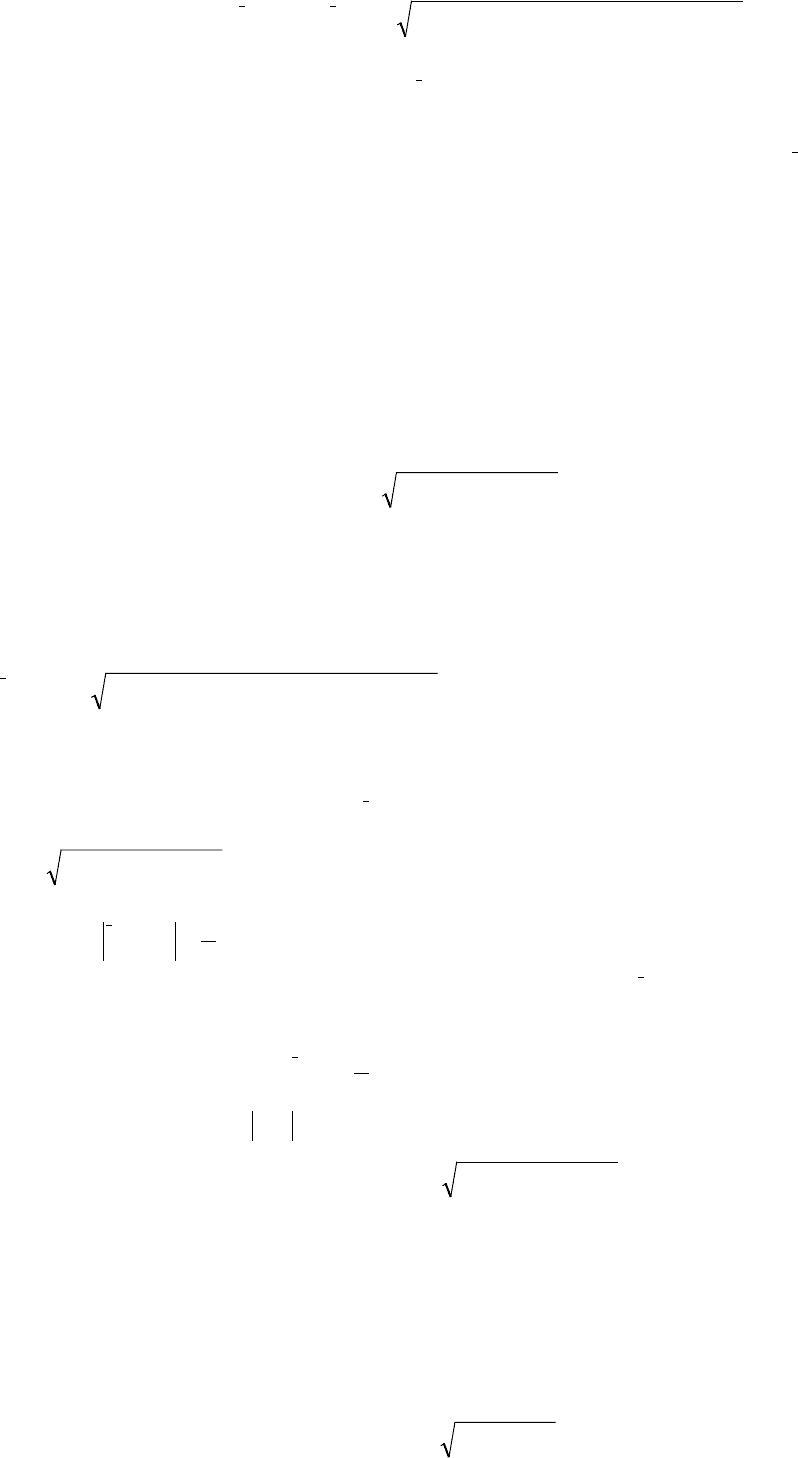
[][ ]
∑∑
−+−==
−−
2
i1i
2
1ii
i
)t()t()t()t(l)T(l
ψψϕϕ
Определение. Если множество
{
}
)T(l длин вписанных в кривую L ломаных,
отвечающих всевозможным разбиением Т [
α,β] ограничено, то кривая L
называется спрямляемой. Точная верхняя грань l множества
{
}
)T(l называется
длиной дуги кривой L.
Теорема (о достаточных условиях спрямляемости и длине дуги плоской кривой).
Если функции
)t(x
ϕ
= и )t(y
ψ
=
имеют на сегменте [α,β] непрерывные
производные, то кривая L, определяемая параметрическими уравнениями
, спрямляема, и длина l ее дуги может быть вычислена по
формуле
[
βα
ψ
ϕ
, t
)t(y
)t(x
∈
=
=
]
[][]
∫
′
+
′
=
β
α
ψϕ
dt)t()t(l
22
(3)
Поясним без детального обоснования схему доказательства данной
теоремы.
Этап 1. Рассматривается выражение
[][ ]
∑
=
−−
−+−=
n
1i
2
i1i
2
i1i
)t()t()t()t()T(l
ψψϕϕ
длины ломаной, вписанной в кривую L и
отвечающей произвольному разбиению Т сегмента [
α,β], и показывается ее
ограниченность, т.е. кривая L - спрямляема. Длина кривой L обозначается через l.
Этап 2. Показывается, что
)T(l сколь угодно мало отличается от величины
[][]
∫
′
+
′
=
β
α
ψϕ
dt)t()t(I
22
при ∆→0, где ∆ - диаметр разбиения Т сегмента [α,β], а
именно,
2
I)T(l
ε
<− (4)
Этап 3. Показывается, что среди ломаных, длины
)T(l которых удовлетворяют
неравенству (4), имеются такие, длины которых мало отличаются от длины l дуги
кривой L, а именно, 0<l-
)T(l <
2
ε
.
Отсюда следует, что
ε
<− Il , и в силу произвольности ε
[][]
∫
′
+
′
==
β
α
ψϕ
22
)t()t(Il
7.10.1. Вычисление длины дуги плоской кривой при различных способах ее
задания
1) Если кривая L является графиком функции y=f(x) и f'(x) непрерывна на [a,b], то
кривая L спрямляема, и длина l ее дуги вычисляется по формуле
[]
∫
′
+=
b
a
2
dx)x(f1l
.
Доказательство. График функции представляет кривую, определяемую
параметрическими уравнениями x=t, y=f(t), a
≤ t ≤ b, и выполнены условия
теоремы о достаточных условиях спрямляемости и длине дуги плоской кривой.
Полагая
ϕ(t)=t, ψ(t)=f(t) и заменяя переменную интегрирования t на x, получим
[]
∫
′
+=
b
a
2
dx)x(f1l
.
2) Кривая L определяется полярным уравнением r=r(θ),θ
1
≤ θ ≤ θ
2
и r(θ) имеет на
[
θ
1
, θ
2
] непрерывную производную, тогда кривая L спрямляема, и длина l дуги L
может быть найдена по формуле
[]
∫
′
+=
2
1
d)(r)(rl
2
2
θ
θ
θθθ
Формула перехода от полярных координат к декартовым координатам
, следовательно, L определяется параметрическими уравнениями, в
которых функции
=
=
θθ
θθ
sin)(ry
cos)(rx
θ
θ
ψ
θ
θ
ϕ
sin)(r ;cos)(r
=
= удовлетворяют условиям теоремы,
откуда следует, что
[][]
()()
[]
∫
∫∫
′
+=
=+
′
+−
′
=
′
+
′
=
2
1
2
1
d)(r)(r
dcosrsinrsinrcosrdt)t()t(l
2
2
2222
θ
θ
θ
θ
β
α
θθθ
θθθθθψϕ
Примеры. 1) Найти длину линии, заданной уравнениями
1yx
3232
=+
Перейдем к параметрическим уравнениям
=
=
tsiny
tcosx
3
3
y
-1 1 x
6
0
2
t2cos3tdt2sin6
dttsintcostcostsin12dttcostsin9tsintcos94l
2
0
2
0
22
2
0
2424
=
Π
−==
=+=+=
∫
∫∫
Π
ΠΠ
2) Найти длину дуги полукубической параболы у
2
=х
3
, заключенной между
точками (0,0) и (4,8).
y
M(4,8)
x
Так как х
≥0, то x
2
3
y =
′
и
()
x
4
9
1y1
2
+=
′
+
Следовательно,
)11010(
27
8
0
4
4
9
1
3
2
9
4
4
9
1
23
4
0
−=
+⋅=+=
∫
xdxxl
3. Найти длину первого витка архимедовой спирали
ρ=аϕ
Первый виток архимедовой спирали
образуется при изменении полярного угла ϕ
от 0 до 2
π
Поэтому
=+=+=
∫∫
ππ
ϕϕϕϕ
2
0
2
2
0
222
d1adaal
(
)
++++=
142ln
2
1
14a
22
ππππ
.
7.11. Квадратируемость и площадь плоской фигуры
Определение 1. Плоской фигурой Q будем называть конечную часть плоскости,
ограниченную простой замкнутой кривой L. Кривая L в этом случае называется
границей фигуры Q.
Будем говорить, что многоугольник вписан в фигуру Q, если каждая точка
этого многоугольника принадлежит фигуре Q или ее границе.
S
i
S
d
Если все точки плоской фигуры и ее
границы принадлежат некоторому
многоугольнику, то говорят, что
указанный многоугольник описан вокруг
фигуры Q. Очевидно, что площадь
любого вписанного в фигуру Q
многоугольника
S
i
не больше площади любого описанного вокруг фигуры Q многоугольника
S
d
(S
i
≤S
d
). Обозначим через
{
и
}
i
S
{
}
d
S числовые множества площадей вписанных в
фигуру Q и описанных вокруг плоской фигуры Q многоугольников. Множество
ограничено сверху (площадью любого описанного вокруг Q многоугольника),
а множество
ограничено снизу (например, числом нуль). Обозначим через
{}
i
S
{
d
S
}
{}
i
SsupP = и
{
d
S
}
infP = . Числа P и P называются нижней и верхней площадью
плоской фигуры Q соответственно.
Лемма. Нижняя площадь
P фигуры Q не больше верхней площади P этой
фигуры, т.е.
P ≤P
sup S P
i
=
PS
d
= inf
Доказательство: Предположим противное, т.е.
P >P и положим
P
PP
+=
+
ε
2
ε
ε
P
S
d
P
PP
−=
+
ε
2
S
i
P
(
)
02PP >=−
ε
. Так как
{
}
i
SsupP
=
, то найдется
такой вписанный в
фигуру Q многоугольник,
площадь S
i
которого
(
)
2PP −PS
i
=−>
ε
(1)
Так как
{}
d
SinfP = , то найдется такой описанный вокруг фигуры Q
многоугольник, площадь которого S
d
будет меньше числа
ε
+P
(
)
2PPPS
d
+=+<
ε
(2).
Из неравенства (1) и (2) следует, что S
d
<S
i
, чего не может быть.
Определение 2. Плоская фигура Q называется квадрируемой, если верхняя
площадь
P этой фигуры совпадает с ее нижней площадью P . При этом число
Р=
P =P называется площадью фигуры Q.
