Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

196 Measurement and Data Analysis for Engineering and Science

ν t

ν,P =50 %

ν,P =90 %

ν,P =95 %

ν,P =99 %

1 1.000 6.341 12.706 63.657

2 0.816 2.920 4.303 9.925

3 0.765 2.353 3.192 5.841

4 0.741 2.132 2.770 4.604

5 0.727 2.015 2.571 4.032

6 0.718 1.943 2.447 3.707

7 0.711 1.895 2.365 3.499

8 0.706 1.860 2.306 3.355

9 0.703 1.833 2.262 3.250

10 0.700 1.812 2.228 3.169

11 0.697 1.796 2.201 3.106

12 0.695 1.782 2.179 3.055

13 0.694 1.771 2.160 3.012

14 0.692 1.761 2.145 2.977

15 0.691 1.753 2.131 2.947

16 0.690 1.746 2.120 2.921

17 0.689 1.740 2.110 2.898

18 0.688 1.734 2.101 2.878

19 0.688 1.729 2.093 2.861

20 0.687 1.725 2.086 2.845

21 0.686 1.721 2.080 2.831

30 0.683 1.697 2.042 2.750

40 0.681 1.684 2.021 2.704

50 0.680 1.679 2.010 2.679

60 0.679 1.671 2.000 2.660

120 0.677 1.658 1.980 2.617

∞ 0.674 1.645 1.960 2.576

TABLE 6.4

Student’s t variable values for diﬀerent P and ν.

Statistics 197

99.73 %

95.45 %

68.27 %

FIGURE 6.5

Student’s t values for various degrees of freedom and percent probabilities.

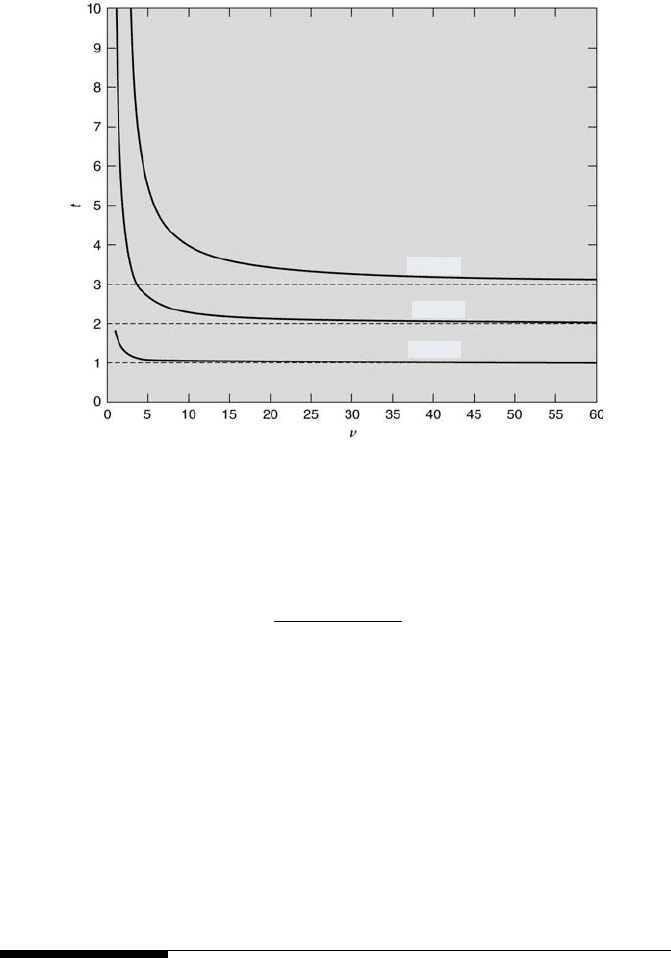
This is

ν,P

= ±



− ¯x) ± z



(% P ). (6.24)

Now, in the limit as N → ∞, the sample mean, ¯x, tends to the true mean, x

and the sample standard deviation, S

, tends to the true standard deviation

σ. It follows from Equation 6.24 that t

ν,P

tends to z

. This is illustrated in

Figure 6.5, in which the t

ν,P

values for P = 68.27 %, 95.45 % and 99.73 %

are plotted versus ν. This ﬁgure was constructed using the MATLAB M-ﬁle

tnuP.m. As shown in the ﬁgure, for increasing values of ν, the t

ν,P

values for

P = 68.27 %, 95.45 % and 99.73 % approach the z

values of 1, 2, and 3,

respectively. In other words, Student’s t distribution approaches the normal

distribution as N tends to inﬁnity.

6.5 Standard Deviation of the Means

Consider a sample of N measurands. From its sample mean, ¯x, and its

sample standard deviation, S

, the region within which the true mean of

the underlying population, x

, can be inferred. This is done by statistically

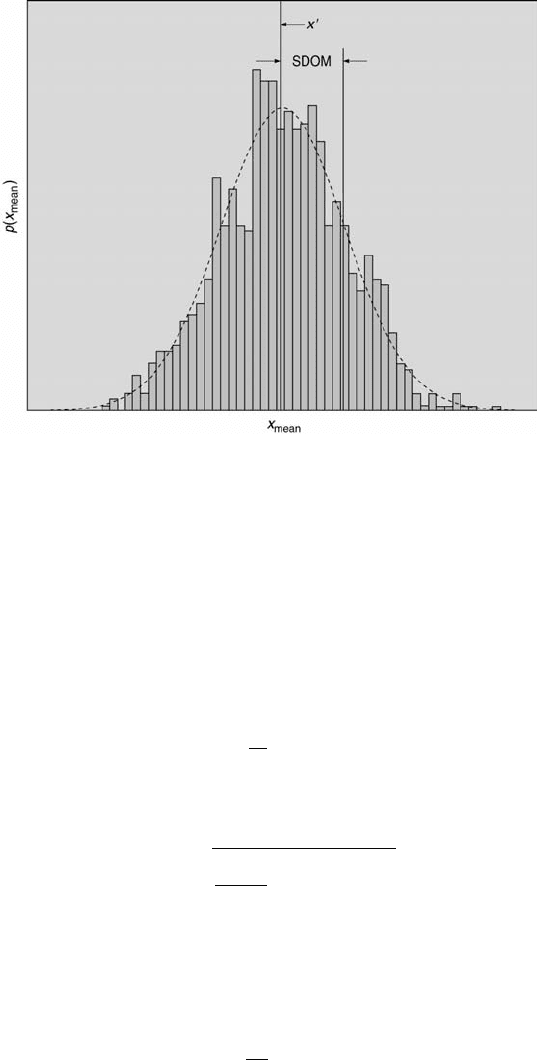
198 Measurement and Data Analysis for Engineering and Science

FIGURE 6.6

The probability density function of the mean values of x.

relating the sample to the population through the standard deviation of

the means (SDOM).

Assume that there are M sets (samples), each comprised of N measur-

ands. A speciﬁc measurand value is denoted by x

, where i = 1 to N refers

to the speciﬁc number within a set and j = 1 to M refers to the particular

set. Each set will have a mean value, ¯x

, where

¯x

i=1

, (6.25)

and a sample standard deviation, S

, where

N − 1

i=1

− ¯x

)

. (6.26)

Now each ¯x

is a random variable. The central limit theorem assures

that the ¯x

values will be normally distributed about their mean value (the

mean of the mean values),

¯x, where

¯x =

j=1

¯x

. (6.27)

Statistics 199

This is illustrated in Figure 6.6.

The standard deviation of the mean values (termed the standard devia-

tion of the means), then will be

¯x





M − 1

j=1

(¯x −

¯x)





1/2

. (6.28)

It can be proven using Equations 6.26 and 6.28 [4] that

¯x

= S

√

N. (6.29)

This deceptively simple formula allows us to determine from the values of

only one ﬁnite set the range of values that contains the true mean value of

the entire population. Formally

= ¯x ± t

ν,P

¯x

= ¯x ± t

ν,P

√

(% P ). (6.30)

This formula implies that the bounds within which x

is contained can be

reduced, which means that the estimate of x

can be made more precise, by

increasing N or by decreasing the value of S

. There is a moral here. It is

better to carefully plan an experiment to minimize the number of random

eﬀects beforehand and hence to reduce S

, rather than to spend the time

acquiring more data to achieve the same bounds on x

The interval ±t

ν,P

¯x

is called the precision interval of the true

mean. As N becomes large, from Equation 6.29 it follows that the SDOM

becomes small and the sample mean value tends toward the true mean value.

In this light, the precision interval of the true mean value can be viewed as

a measure of the uncertainty in determining x

Example Problem 6.4

Statement: Consider the diﬀerential pressure transducer measurements in the pre-

vious example. What is the range within which the true mean value of the diﬀerential

pressure, p

, is contained?

Solution: Equation 6.30 reveals that

= ¯p ± t

ν,P

¯p

= ¯p ± t

ν,P

√

(% P )

= 4.97 ±

(2.101)(0.046)

√

= 4.97 ± 0.02 (95 %)

Thus, the true mean value is estimated at 95 % conﬁdence to be within the range from

4.95 kPa to 4.99 kPa.

Finally, it is very important to note that although Equations 6.23 and

6.30 appear to be similar, they are uniquely diﬀerent. Equation 6.23 is used

to estimate the range within which another x

value will be with a given

200 Measurement and Data Analysis for Engineering and Science

conﬁdence, whereas Equation 6.30 is used to estimate the range that con-

tains the true mean value for a given conﬁdence. Both equations use the

values of the sample mean, standard deviation, and number of measurands

in making these estimates.

6.6 Chi-Square Distribution

The range that contains the true mean of a population can be estimated

using the values from only a single sample of N measurands and Equa-

tion 6.30. Likewise, there is an analogous way of estimating the range that

contains the true variance of a population using the values from only one

sample of N measurands. The estimate involves using one more probability

distribution, the chi-square distribution.

The chi-square distribution is used in many statistical calculations. For

example, it can be used to determine the precision interval of the true vari-

ance, to quantify how well a sample matches an assumed parent distribution,

and to compare two samples of same or diﬀerent size with one another. The

statistical variable, χ

, represents the sum of the squares of the diﬀerences

between the measured and expected values normalized by their variance.

Thus, the value of χ

is dependent upon the number of measurements, N,

at which the comparison is made, and, hence, the number of degrees of free-

dom, ν = N − 1. From this deﬁnition it follows that χ

is related to the

standardized variable, z

= (x

− x

)/σ, and the number of measurements

i=1

− x

)

. (6.31)

can be viewed as a quantitative measure of the total deviation of all

values from their population’s true mean value with respect to their

population’s standard deviation. This concept can be used, for example, to

compare the χ

value of a sample with the value that would be expected for

a sample of the same size drawn from a normally distributed population.

Using the deﬁnition of the sample variance given in Equation 6.21, this

expression becomes

= νS

/σ

. (6.32)

So, in the limit as N → ∞, χ

→ ν.

The probability density function of χ

(for χ

≥ 0) is

p(χ

, ν) = [2

ν/2

Γ(ν/2)]

−1

(χ

)

(ν/2)−1

exp(−χ

/2), (6.33)

where Γ denotes the gamma function given by

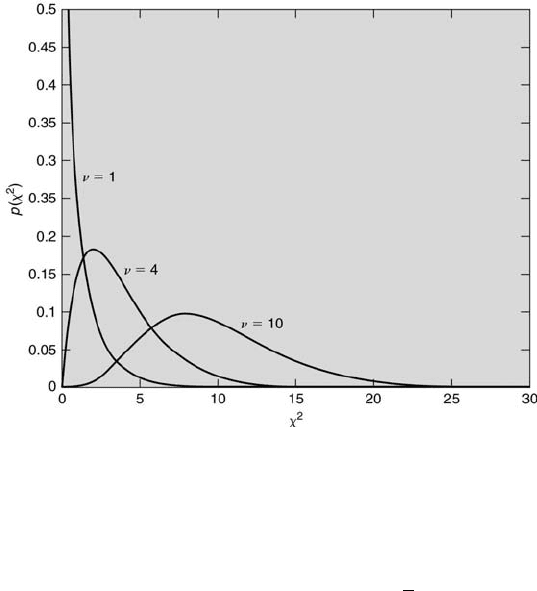
Statistics 201

FIGURE 6.7

Three χ

probability density functions.

Γ(ν/2) =

∞

(ν/2)−1

exp(−x)dx = (

− 1)! (6.34)

and the mean and the variance of p(χ

, ν) are ν and 2ν, respectively. Some-

times values of χ

are normalized by the expected value, ν. The appropriate

parameter then becomes the reduced chi-square variable, which is de-

ﬁned as

≡ χ

/ν. The mean value of the reduced chi-square variable

then equals unity. Finally, note that there is a diﬀerent probability density

function of χ

for each value of ν.

The χ

probability density functions for three diﬀerent values of ν are

plotted versus χ

in Figure 6.7. The MATLAB M-ﬁle chipdf.m was used

to construct this ﬁgure. The value of p(χ

= 10, ν = 10) is 0.0877, whereas

the value of p(χ

= 1, ν = 1) is 0.2420. For a sample of only N = 2

(ν = N − 1 = 1), there is almost a 100 % chance that the value of χ

will

be less than approximately 9. However, if N = 11 there is approximately a

50 % chance that the value of χ

will be less than approximately 9.

The corresponding probability distribution function, given by the inte-

gral of the probability density function from 0 to a speciﬁc value of χ

denoted by χ

, is called the chi-square distribution with ν degrees of free-

dom. It denotes the probability P (χ

) = 1 − α that χ

≤ χ

, where α

denotes the level of signiﬁcance. In other words, the area under a spe-

ciﬁc χ

probability density function curve from 0 to χ

equals P (χ

) and

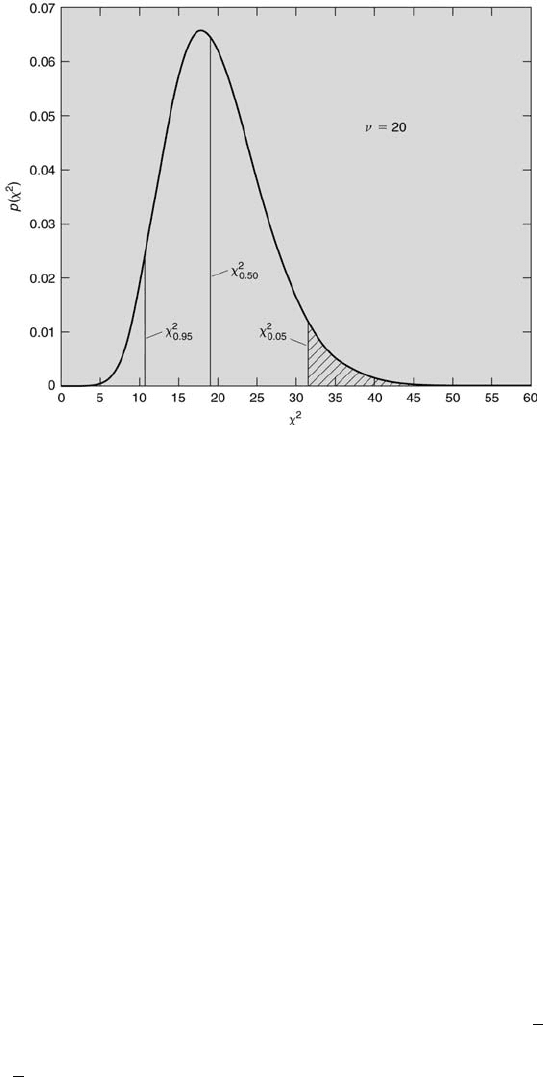
202 Measurement and Data Analysis for Engineering and Science

FIGURE 6.8

The χ

probability density function for ν = 20.

the area from χ

to ∞ equals α. The χ

probability density function for

ν = 20 is plotted in Figure 6.8. The MATLAB M-ﬁle chicdf.m was used

to construct this ﬁgure. Three χ

values (for α = 0.05, 0.50, and 0.95) are

indicated by vertical lines. The lined area represents 5 % of the total area

under the probability density curve, corresponding to α = 0.05. The χ

values for various ν and α are presented in Table 6.5. Using this table, for

ν = 20, χ

0.95

= 10.9, χ

0.50

= 19.3, and χ

0.05

= 31.4. That is, when ν = 20,

50 % of the area beneath the curve is between χ

= 0 and χ

= 19.3.

The χ

probability distribution functions for the same values of ν used

in Figure 6.7 are plotted versus χ

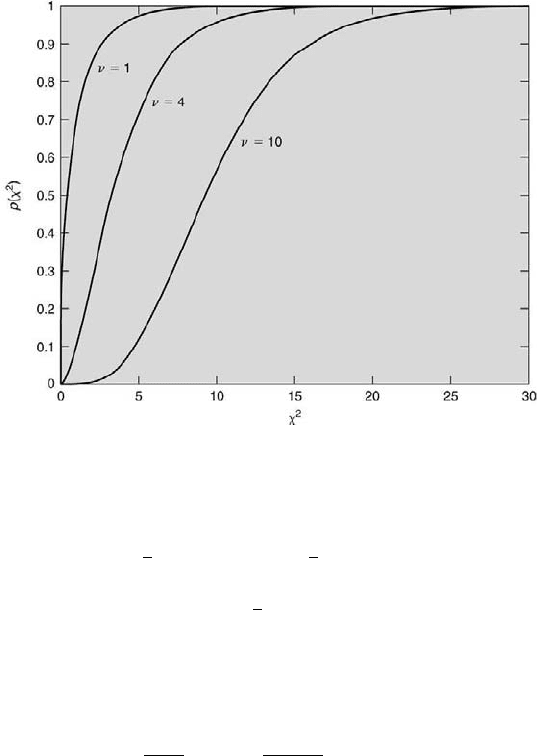
in Figure 6.9. For N = 2, there is a

99.73 % chance that the value of χ

will be less than 9. For N = 11, there

is a 46.79 % chance that the value of χ

will be less than 9. Finally, for

ν = 4, as already determined using Table 6.5, a value of χ

= 3.36 yields

P (χ

) = 0.50.

6.6.1 Estimating the True Variance

Consider a ﬁnite set of x

values drawn randomly from a normal distribution

having a true mean value x

and a true variance σ

. It follows directly from

Equation 6.32 and the deﬁnition of χ

that there is a probability of 1−

that

νS

/σ

≤ χ

α/2

or that νS

/χ

α/2

≤ σ

. Conversely, there is a probability of

1 − (1 −

) = α/2 that σ

≤ νS

/χ

α/2

. Likewise, there is a probability of

Statistics 203

ν χ

0.99

0.975

0.95

0.90

0.50

0.05

0.025

0.01

1 0.000 0.000 0.000 0.016 0.455 3.84 5.02 6.63

2 0.020 0.051 0.103 0.211 1.39 5.99 7.38 9.21

3 0.115 0.216 0.352 0.584 2.37 7.81 9.35 11.3

4 0.297 0.484 0.711 1.06 3.36 9.49 11.1 13.3

5 0.554 0.831 1.15 1.61 4.35 11.1 12.8 15.1

6 0.872 1.24 1.64 2.20 5.35 12.6 14.4 16.8

7 1.24 1.69 2.17 2.83 6.35 14.1 16.0 18.5

8 1.65 2.18 2.73 3.49 7.34 15.5 17.5 20.1

9 2.09 2.70 3.33 4.17 8.34 16.9 19.0 21.7

10 2.56 3.25 3.94 4.78 9.34 18.3 20.5 23.2

11 3.05 3.82 4.57 5.58 10.3 19.7 21.9 24.7

12 3.57 4.40 5.23 6.30 11.3 21.0 23.3 26.2

13 4.11 5.01 5.89 7.04 12.3 22.4 24.7 27.7

14 4.66 5.63 6.57 7.79 13.3 23.7 26.1 29.1

15 5.23 6.26 7.26 8.55 14.3 25.0 27.5 30.6

16 5.81 6.91 7.96 9.31 15.3 26.3 28.8 32.0

17 6.41 7.56 8.67 10.1 16.3 27.6 30.2 33.4

18 7.01 8.23 9.39 10.9 17.3 28.9 31.5 34.8

19 7.63 8.91 10.1 11.7 18.3 30.1 32.9 36.2

20 8.26 9.59 10.9 12.4 19.3 31.4 34.2 37.6

30 15.0 16.8 18.5 20.6 29.3 43.8 47.0 50.9

40 22.2 24.4 26.5 29.1 39.3 55.8 59.3 63.7

50 29.7 32.4 34.8 37.7 49.3 67.5 71.4 76.2

60 37.5 40.5 43.2 46.5 59.3 79.1 83.3 88.4

70 45.4 48.8 51.7 55.3 69.3 90.5 95.0 100.4

80 53.5 57.2 60.4 64.3 79.3 101.9 106.6 112.3

90 61.8 65.6 69.1 73.3 89.3 113.1 118.1 124.1

100 70.1 74.2 77.9 82.4 99.3 124.3 129.6 135.8

TABLE 6.5

values for various ν and α.

204 Measurement and Data Analysis for Engineering and Science

FIGURE 6.9

Three χ

probability distribution functions.

α/2 that νS

/σ

≤ χ

1−

or that νS

/χ

1−

≤ σ

. Thus, the true variance

of the underlying population, σ

, is within the sample variance precision

interval, from νS

/χ

α/2

to νS

/χ

1−

with a probability 1−(α/2)−(α/2) =

P . Also there is a probability α/2 that it is below the lower bound of the

precision interval, a probability α/2 that it is above the upper bound of the

precision interval, and a probability α that it is outside of the bounds of the

precision interval. Formally, this is

νS

α/2

≤ σ

≤

νS

1−α/2

(% P ). (6.35)

The width of the precision interval of the true variance in relation to

the probability P can be examined further. First consider the two extreme

cases. If P = 1 (100 %), then α = 0 which implies that χ

= ∞ and χ

= 0.

Thus, the sample variance precision interval is from 0 to ∞ according to

Equation 6.35. That is, there is a 100 % chance that σ

will have a value

between 0 and ∞. If P = 0 (0 %), then α = 1 which implies that the sample

variance precision intervals are the same. That is, there is a 0 % chance the

will exactly equal one speciﬁc value out of an inﬁnite number of possible

values (when α = 1 and ν >> 1, that unique value would be S

). These two

extreme-case examples illustrate the upper and lower limits of the sample

variance precision interval and its relation to P and α. As α varies from 0 to

1 (hence, P varies from 1 to 0), the precision interval width decreases from

Statistics 205

∞ to 0. In other words, the probability, α, that the true variance is outside

of the sample variance precision interval increases as the precision interval

width decreases.

6.6.2 Establishing a Rejection Criterion

The relation between the probability of occurrence of a χ

value being less

than a speciﬁed χ

value can be utilized to ascertain whether or not eﬀects

other than random ones are present in an experiment or process. This is

particularly relevant, for example, in establishing a rejection criterion for a

manufacturing process or in an experiment. If the sample’s χ

value exceeds

the value of χ

based upon the probability of occurrence P = 1 − α, it is

likely that systematic eﬀects (biases) are present. In other words, the level of

signiﬁcance α also can be used as a chance indicator of random eﬀects. A low

value of α implies that there is very little chance that the noted diﬀerence

is due to random eﬀects and, thus, that a systematic eﬀect is the cause for

the discrepancy. In essence, a low value of α corresponds to a relatively high

value of χ

, which, of course, has little chance to occur randomly. It does,

however, have some chance to occur randomly, which leads to the possibility

of falsely identifying a random eﬀect as being systematic, which is a Type II

error (see Section 6.8). For example, a batch sample yielding a low value of α

implies that the group from which it was drawn is suspect and probably (but

not deﬁnitely) should be rejected. A high value of α implies the opposite,

that the group probably (but not deﬁnitely) should be accepted.

Example Problem 6.5

Statement: This problem is adapted from [18]. A manufacturer of bearings has

compiled statistical information that shows the true variance in the diameter of “good”

bearings is 3.15 µm

. The manufacturer wishes to establish a batch rejection criterion

such that only small samples need to be taken and assessed to check whether or not

there is a ﬂaw in the manufacturing process that day. The criterion states that when

a batch sample of 20 manufactured bearings has a sample variance > 5.00 µm

the

batch is to be rejected. This is because, most likely, there is a ﬂaw in the manufacturing

process. What is the probability that a batch sample will be rejected even though the

true variance of the population from which it was drawn was within the tolerance limits

or, in other words, of making a Type II error?

Solution: From Equation 6.32,

(ν) = νS

/σ

(20 − 1)(5.00)

(3.15)

= 30.16.

For this value of χ

and ν = 19, α

∼

0.05 using Table 6.5. So, there is approximately

a 5 % chance that the discrepancy is due to random eﬀects (that a new batch will be

rejected even though its true variance is within the tolerance limits), or a 95 % chance

that it is not. Thus, the standard for rejection is good. That is, the manufacturer should

reject any sample that has S

> 5 µm

. In doing so, he risks only a 5 % chance of

falsely identifying a good batch as bad. If the χ

value equaled 11.7 instead, then there

would be a 90 % chance that the discrepancy is due to random eﬀects.

Now what if the size of the batch sample was reduced to N = 10? For this case,

α = 0.0004. So, there is a 0.04 % chance that the discrepancy is due to random eﬀects.