Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

166 Measurement and Data Analysis for Engineering and Science

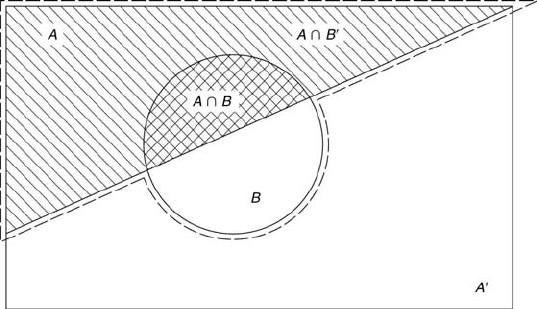
FIGURE 5.17

The union and the intersection of the sets A and B.

A and the circular region the set of events B. The complement of A is

denoted by A

. The sample space is exhaustive because A and A

comprise

the entire sample space. For two sets A and B, the union is the set of

all members of A or B or both, as denoted by the region bordered by the

dashed line. This is written as P r[A ∪ B].

If the sets of A and B are mutually exclusive where they do not share

any common members, then

P r[A ∪ B] = P r[A] + P r[B]. (5.30)

This would be the case if the sets A and B did not overlap in the ﬁgure (if

the circular region was outside the triangular region). Thus, the probability

of getting 3 or 4 in the eight-toss experiment is 1/4 (from 3 and 4).

If the sets do overlap and have common members, as shown by the cross-

hatched region in the ﬁgure, then

P r[A ∪ B] = P r[A] + P r[B] − P r[A ∩ B], (5.31)

where P r[A ∩ B] is the probability of the intersection of A and B. The

intersection is the set of all members in both A and B. So, the correct way

to compute the desired probability is P r[even∪3∪4] = P r[even] + P r[3] +

P r[4] − P r[even∩3∩4] = 3/8 + 1/8 + 1/8 − 1/8 = 1/2. P r[even∩3∩4] =

1/8, because only one common member, 4, occurred during the eight tosses.

5.9.2 *Conditional Probability

The moment questions are asked such as, “What is the chance of getting a 4

on the second toss of a die given either a 1 or a 3 was rolled on the ﬁrst toss?”,

Probability 167

more thought is required to answer them. This is a problem in conditional

probability, the probability of an event given that speciﬁed events have

occurred in the past. This concept can be formalized by determining the

probability that event B occurs given that event A occurred previously.

This is written as P r[B | A], where

P r[B | A] ≡

P r[B ∩ A]

P r[A]

. (5.32)

Rearranging this deﬁnition gives

P r[B ∩ A] = P r[B | A]P r[A]. (5.33)

This is known as the multiplication rule of conditional probability. Further,

because P r[A ∩ B] = P r[B ∩ A], Equation 5.33 implies that

P r[B | A]P r[A] = P r[A | B]P r[B]. (5.34)

Examination of Figure 5.17 further reveals that

P r[A] = P r[A ∩ B] + P r[A ∩ B

], (5.35)

where A ∩ B

is shown as the lined region and B

means not B. Using the

converse of Equation 5.33, Equation 5.35 becomes

P r[A] = P r[A | B]P r[B] + P r[A | B

]P r[B

]. (5.36)

Equation 5.36 is known as the total probability rule of conditional probabil-

ity. It can be extended to represent more than two mutually exclusive and

exhaustive events [6].

When events A and B are mutually exclusive, then P r[B | A] = 0,

which leads to P r[B ∩ A] = 0. When event B is independent of event A,

the outcome of event A has no inﬂuence on the outcome of event B. Then

P r[B | A] = P r[B]. (5.37)

Thus, for independent events, it follows from Equations 5.33 and 5.37 that

P r[B ∩ A] = P r[B]P r[A]. (5.38)

That is, the conditional probability of a series of independent events is the

product of the individual probabilities of each of the events. Hence, to answer

the question posed at the beginning of this section, P r[B ∩ A] = P r[A]

P r[B] = (1/6)(2/6) = 2/36. That is, there is approximately a 6 % chance

that either an even number or the numbers 3 or 4 occurred.

The chance of winning the lottery can be determined easily using this

information. The results suggest not to bet in lotteries. Assume that four

balls are drawn from a bin containing white balls numbered 1 through 49,

and then a ﬁfth ball is drawn from another bin containing red balls with

168 Measurement and Data Analysis for Engineering and Science

the same numbering scheme. Because each number selection is indepen-

dent of the other number selections, the probability of guessing the num-

bers on the four white balls correctly would be P r[1] P r[2] P r[3] P r[4] =

(1/49)(1/48)(1/47)(1/46) = 1/(5 085 024). The probability of guessing the

numbers on all ﬁve balls correctly would be Pr[1] Pr[2] Pr[3] Pr[4] Pr[5] =

[1/(5 085 024)](1/49) = 1/(249 166 176) or about 1 chance in 250 million!

That chance is about equivalent to tossing a coin and getting 28 heads in

a row. Recognizing that the probability that an event will not occur equals

one minus the probability that it will occur, the chance of not winning the

lottery is 99.999 999 6 %. So, it is very close to impossible to win the lottery.

Other useful conditional probability relations can be developed. Using

Equation 5.34 and its converse, noting that P r[A ∩ B] = P r[B ∩ A],

P r[B | A] =

P r[B]P r[A | B]

P r[A]

. (5.39)

This relation allows us to determine the probability of event B occurring

given that event A has occurred from the probability of event A occurring

given that event B has occurred.

Example Problem 5.7

Statement: Determine the probability that the temperature, T , will exceed 100

◦

F in a storage tank whenever the pressure, p, exceeds 2 atmospheres. Assume the

probability that the pressure exceeds 2 atmospheres whenever the temperature exceeds

100

◦

F is 0.30, the probability of the pressure exceeding 2 atmospheres is 0.10 and the

probability of the temperature exceeding 100

◦

F is 0.25.

Solution: Formally, P r[p > 2 | T > 100] = 0.30, P r[p¿2] = 0.10 and P r[T >100] =

0.25. Using Equation 5.39, P r[T > 100 | p >2] = (0.25)(0.30)/(0.10) = 0.75. That is,

whenever the pressure exceeds 2 atmospheres there is a 75 % chance that the temper-

ature will exceed 100

◦

Equation 5.36 can be substituted into Equation 5.39 to yield

P r[B | A] =

P r[A | B]P r[B]

P r[A | B]P r[B] + P r[A | B

]P r[B

]

. (5.40)

This equation expresses what is known as Bayes’ rule, which is valid for

mutually exclusive and exhaustive events. It was discovered accidentally

by the Reverend Thomas Bayes (1701-1761) while manipulating formulas

for conditional probability [1]. Its power lies in the fact that it allows one

to calculate probabilities inversely, to determine the probability of a before

event conditional upon an after event. This equation can be extended to

represent more than two events [6]. Bayes’ rule can be used to solve many

practical problems in conditional probability. For example, the probability

that a component identiﬁed as defective by a test of known accuracy ac-

tually is defective can be determined knowing the percentage of defective

components in the population.

Probability 169

Before determining this probability speciﬁcally, examine these types of

probabilities in a more general sense. Assume that the probability of an

event occurring is p

. A test can be performed to determine whether or not

the event has occurred. This test has an accuracy of 100p

percent. That

is, it is correct 100p

percent of the time and incorrect 100(1 − p

) percent

of the time. What is the percent probability that the test can predict an

actual event? There are four possible situations that can arise: (1) the test

indicates that the event has occurred and the event actually has occurred

(a true positive), (2) the test indicates that the event has occurred and the

event actually has not occurred (a false positive), (3) the test indicates that

the event has not occurred and the event actually has occurred (a false neg-

ative), and (4) the test indicates that the event has not occurred and the

event actually has not occurred (a true negative). Here, the terms positive

and negative refer to the indicated occurrence of the event and the terms

true and false refer to whether or not the indicated occurrence agrees with

the actual occurrence of the event. So, the probabilities of the four possible

combinations of events are p

for true positive, (1 − p

)(1 − p

) for false

positive, (1 −p

for false negative, and p

(1 −p

) for true negative. Now

the probability that an event actually occurred given that a test indicated

that it had occurred would be the ratio of the actual probability of occur-

rence (the true positive probability) to the sum of all indicated positive

occurrences (the true positive plus the false positive probabilities). That is,

P r[A | IA] =

+ (1 − p

)(1 − p

)

, (5.41)

where IA denotes the event of an indicated occurrence of A and A symbolizes

the event of an actual occurrence.

Alternatively, Equation 5.41 can be derived directly using Bayes’ rule.

Here,

P r[A | IA] =

P r[IA | A]P r[A]

P r[IA | A]P r[A] + P r[IA | A

]P r[A

]

, (5.42)

which is identical to Equation 5.41 because Pr[IA | A] = p

, Pr[A] = p

Pr[IA | A

] = (1 - p

) and Pr[A

] = (1 - p

Example Problem 5.8

Statement: An experimental technique is being developed to detect the removal

of a microparticle from the surface of a wind tunnel wall as the result of a turbulent

sweep event. Assume that a sweep event occurs 14 % of the time when the detection

scheme is operated. The experimental technique can detect a sweep event correctly 73

% of the time. [a] What is the probability that a sweep event will be detected during

the time period of operation? [b] What is the probability that a sweep event will be

detected if the experimental technique is correct 90 % of the time?

Solution: The desired probability is the ratio of true positive identiﬁcations to

true positive plus false positive identiﬁcations. Let p

be the probability of an actual

sweep event occurrence during the time period of operation and p

be the experimental

170 Measurement and Data Analysis for Engineering and Science

technique’s reliability (the probability to identify correctly). For this problem, p

= 0.14

and p

= 0.73 for part [a] and p

= 0.90 for part [b]. Substitution of these values into

Equation 5.41 yields P = 0.31 for part [a] and P = 0.59 for part [b]. First, note that

the probability that a sweep event will be detected is only 31 % with a 73 % reliability

of the experimental technique. This in part is because of the relatively low percentage

of sweep event occurrences during the period of operation. Second, an increase in the

technique’s reliability from 73 % to 90 %, or by 17 %, increases the probability from

31 % to 59 %, or by 28 %. An increase in technique reliability increases the probability

of correct detection relatively by a greater amount.

Example Problem 5.9

Statement: Suppose that 4 % of all transistors manufactured at a certain plant

are defective. A test to identify a defective transistor is 97 % accurate. What is the

probability that a transistor identiﬁed as defective actually is defective?

Solution: Let event A denote that the transistor actually is defective and event B

that the transistor is indicated as defective. What is P r[A | B]? It is known that P r[A]

= 0.04 and P r[B | A] = 0.97. It follows that Pr[A

] = 1 − P r[A] = 0.96 and Pr[B | A

]

= 1 − P r[B | A] = 0.03 because the set of all possible events are mutually exclusive

and exhaustive. Direct application of Bayes’ rule gives

P r[A | B] =

(0.97)(0.04)

(0.97)(0.04) + (0.03)(0.96)

= 0.57.

So, there is a 57 % chance that a transistor identiﬁed as defective actually is defective.

At ﬁrst glance, this percentage seems low. Intuitively, the value would be expected to

be closer to the accuracy of the test (97 %). However, this is not the case. In fact, to

achieve a 99 % chance of correctly identifying a defective transistor, the test would

have to be 99.96 % accurate!

It is important to note that the way statistics are presented, either in the

form of probabilities, percentages, or absolute frequencies, makes a notice-

able diﬀerence to some people in arriving at the correct result. Studies [6]

have shown that when statistics are expressed as frequencies, a far greater

number of people arrive at the correct result. The previous problem can be

solved again by using an alternative approach [6].

Example Problem 5.10

Statement: Suppose that 4 % of all transistors manufactured at a certain plant

are defective. A test to identify a defective transistor is 97 % accurate. What is the

probability that a transistor identiﬁed as defective actually is defective?

Solution:

• Step 1: Determine the base rate of the population, which is the fraction of defective

transistors at the plant (0.04).

• Step 2: Using the test’s accuracy and the results of the ﬁrst step, determine the

fraction of defective transistors that are identiﬁed by the test to be defective (0.04

× 0.97 = 0.04).

• Step 3: Using the fraction of good transistors in the population and the test’s false-

positive rate (1 − 0.97 = 0.03), determine the fraction of good transistors that are

identiﬁed by the test to be defective (0.96 × 0.03 = 0.03).

Probability 171

• Step 4: Determine the desired probability, which is 100 times the fraction in step 2

divided by the sum of the fractions in steps 2 and 3 (0.04 / [0.04 + 0.03] = 0.57) or

57 %.

Which approach is easier to understand?

5.9.3 *Coincidences

Conditional probability can be used to explain what appear to be rare co-

incidences. My wife and I took a tour of Scotland in 1999 along with ﬁve

other people whom we had never met before. When we boarded the tour

bus in Scotland we were astounded to ﬁnd out that ﬁve out of the seven of

us lived in Indiana! Our reaction was common − what a rare coincidence,

especially because only about one out of every 1000 people in the world

(approximately 0.1 %) live in Indiana and about 3/4 of us on the bus were

from Indiana. But then I started to think and ask questions. It turns out

that the United Kingdom is a very popular vacation spot for people from

the midwestern and eastern United States and that a commercial airline was

having a special oﬀer that included a ﬂight and tour of Scotland for those

ﬂying out of Chicago’s O’Hare and New York City’s Kennedy airports (all

of those on the bus lived near Chicago or New York City). Granted these

conditions do not explain why ﬁve people from Indiana versus another mid-

western or eastern state were there, but they do make this coincidence much

more probable and certainly not rare.

As remarked by Stewart [2], “Because we notice coincidences and ignore

noncoincidences, we make coincidences seem more signiﬁcant than they re-

ally are.” In fact, even today many people still attribute the occurrences of

apparently rarely occurring events to mysterious causes. Perhaps it is eas-

ier to believe in an inexplicable cause than to identify the conditions under

which the event occurred. Most likely, such occurrences are not so rare after

all.

5.9.4 *Permutations and Combinations

The probability of an event can be determined knowing the number of oc-

currences of the event and the total number of occurrences of all possible

events. Finding the number of all possible events can sometimes be confus-

ing. Consider an experiment in which there are three possible occurrences

denoted by a, b, and c, each of which can occur only once without replace-

ment. What is the probability of getting c, then a, then b, which is P r[cab]?

To determine this probability, the total number of ways that a, b, and c can

be arranged respective of their order must be known. That is, the number

of permutations of a, b, and c must be determined. The number of permu-

tations of n objects is

172 Measurement and Data Analysis for Engineering and Science

n! = n(n − 1)(n − 2)...1, (5.43)

where n! is called n factorial. Stirling’s formula is sometimes useful, where

n! '

√

2πn(n/ exp(n))

, which agrees with Equation 5.43 within 1 % for

n > 9. So, there are six possible ways (abc, acb, bca, bac, cab, and cba) to

arrange a, b, and c. Thus, Pr[cab] = 1/6.

Now what if the experiment had four possible occurrences, a, b, c, and

d, and P r[cab] needs to be determined? The number of permutations of n

objects taken m at a time, P

, is

(n − m)!

= n(n − 1)(n − 2)...(n − m + 1). (5.44)

So, there are 4!/(4-3)! or 24 possible ways to arrange three of the four possi-

ble occurrences. Thus, Pr[cab] = 1/24. The probability of getting c, then a,

then b is reduced from 1/6 to 1/24 when the possibility of a fourth occurrence

is introduced. Often it is easy to calculate the number of permutations using

a spread sheet program. For example, using Microsoft EXCEL, the value of

Equation 5.44 is given by the command PERMUT(n,m).

Further consider the same experiment, but where the number of possible

combinations of c, a, and b are determined irrespective of the order. That

is, the number of combinations of n objects taken m at a time, C

, given

m!(n − m)!

n(n − 1)(n − 2)...(n − m + 1)

, (5.45)

must be found. There are only 4!/(3!1!) or four possible combinations of

three out of four possible occurrences (abc, abd, cdb, and cda). So, the P r[cab]

= 1/4 for this case. That is, there is a ten-time greater chance (25 % versus

2.5 %) of getting a, b, and c in any order versus getting the particular order

of c, a, and b. Using Microsoft EXCEL, the value of Equation 5.45 is given

by the command COMBIN(n,m).

Finally, if there is repetition with replacement, then the number of possi-

ble combinations of n objects taken m at a time with replacement, C

m(r)

(m + n − 1)!

(m!)(n − 1)!

. (5.46)

For our experiment, Equation 5.46 gives 6!/(3!3!) or 20 possible combina-

tions of three out of four possible occurrences. This leads to P r[cab] = 1/20.

Clearly, when there is repetition, the number of possible combinations in-

creases.

Probability 173

5.9.5 *Birthday Problems

There are two classic birthday problems that challenge one’s ability to com-

pute the probability of an occurrence [1]. The ﬁrst is to determine the prob-

ability of at least two out of n people having the same birth date of the year

(same day and month but not necessarily the same year). The second is to

determine the probability of at least two out of n people having a speciﬁc

birth date, such as January 18th. For simplicity, assume that there are 365

days per year and that the probability of having a birthday on any day of

the year is the same (both assumptions are, in fact, not true).

Consider the ﬁrst problem. Often it is easier ﬁrst to compute the proba-

bility that an event will not occur and then subtract that probability from

unity to obtain the probability that the event will occur. For the second

person there is a probability of 364/365 (= [366 − n]/365 where n = 2) of

not having the same birth date of the year as the ﬁrst person. For the third

person it is (364/365)(363/365) of not having the same birth date of the year

as the ﬁrst person or the second person. Here each event is independent of

the other, so the joint probability is the product of the two. Continuing this

logic, the probability, Q, of n people not having the same birth date of the

year is

Q =

364

365

363

365

· · ·

(366 − n)

365

. (5.47)

With a little algebra and using the deﬁnition of the factorial, Equation 5.47

can be rewritten as

Q =

365

365!

(365 − n)!

365

. (5.48)

Thus, the probability, P , of at least two of n people having the same birth

date of the year is

P = 1 − Q = 1 −

365

. (5.49)

For n = 10, Equation 5.49 gives P = 11.69 % and for n = 50, P = 97.04 %.

How many people have to be in a room to have a greater than 50 % chance

of at least two people having the same birth date of the year? The answer

is at least 23 people (P = 50.73 %).

Now examine the second problem, which diﬀers from the ﬁrst problem

in that a speciﬁc birth date is speciﬁed. The probability of the second of n

people not having that speciﬁc birth date is (364/365) and the probability

of the third of n people not having that speciﬁc birth date is the same, and

so on. Thus, the probability of n people not having a speciﬁc birth date is

Q =



364

365



n−1

. (5.50)

174 Measurement and Data Analysis for Engineering and Science

The probability of at least two of n people having a speciﬁc birth date of

the year is

P = 1 − Q = 1 −



364

365



n−1

. (5.51)

For n = 10, Equation 5.51 gives P = 2.44 % and for n = 50, P = 12.58

%. So how many people have to be in a room to have a greater than 50 %

chance of at least two people having a speciﬁc birth date of the year? The

answer is at least 254 people (P = 50.05 %).

Probability 175

5.10 Problem Topic Summary

Topic

Review Problems

Homework Problems

Basic Probability

1, 2, 3, 11, 14, 15

Conditional Probability

10, 16, 17, 18

2, 3, 10

Moments

6, 7, 8, 9, 13

7, 9

Displaying Probabilities

4, 5, 12

4, 5, 6, 8

TABLE 5.2

Chapter 5 Problem Summary

5.11 Review Problems

1. Assuming equal probability of being born any day of the year, match

each of the following birthday occurrence possibilities (for one person)

with its correct probability given in Table 5.3.

2. One of each US coin currencies is placed into a container (a penny, a

nickel, a dime, and a quarter). Given that the withdrawal of a coin from

the container is random, ﬁnd the correct value for each of the following

described quantities: (a) If two coins are drawn, ﬁnd the probability of

any one permutation occurring. (b) If three coins are drawn without re-

placement, ﬁnd the probability of the total being the maximum possible

monetary value. (c) If three coins are drawn with replacement, ﬁnd the

probability of the total being the maximum possible monetary value.

(d) If two coins are drawn with replacement, ﬁnd the probability of the

total number of cents being even.

Possibility of Occurrence

Probability

on the 31st of a month

0.0849

in August

0.329

on Feb. 29, 1979 (for one born in that year)

in a month with 30 days

0.0192

TABLE 5.3

Birthday occurrences and probabilities.