Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

206 Measurement and Data Analysis for Engineering and Science

In other words, getting a χ

value of 30.16 with a batch sample of 10 instead of 20

gives us even more assurance that the criterion is a good one.

6.6.3 Comparing Observed and Expected Distributions

In some situations, a sample distribution should be compared with an ex-

pected distribution to determine whether or not the expected distribution

actually governs the underlying process. When comparing two distributions

using a χ

analysis,

≈

j=1

− E

)

, (6.36)

with O

and E

the number of observed and expected occurrences in the j -th

bin, respectively. The expected occurrence for the j -th bin is the product of

the total number of occurrences, N , and the probability of occurrence, P

The probability of occurrence is the diﬀerence of the probability distribution

function’s values at the j -th bin’s two end points. It also can be approxi-

mated by the product of the bin width and the probability density function

value at the bin’s mid-point value. Equation 6.36 follows from Equation 6.31

by noting that σ

∼ ν ∼ E. Strictly speaking, this expression is an approx-

imation for χ

and is subject to the additional constraint that E

≥ 5 [7].

The number of degrees of freedom, ν, are given by ν = K −(L + n), where

K is the number of bins, preferably using Scott’s formula for equal-width

intervals that was described in Section 5.4. Here, n = 2 because two values

are needed to compute the expected probabilities from the assumed distri-

bution (one for the mean and one for the variance). There is an additional

constraint (L = 1), because the number of expected values must be deter-

mined. Thus, whenever χ

analysis of this type is performed, ν = K − 3.

From this type of analysis, agreement between observed and expected

distributions can be ascertained with a certain conﬁdence. The percent

probability that the expected distribution is the correct one is speciﬁed

by α. By convention, when α < 0.05, the disagreement between the sample

and expected distributions is signiﬁcant or the agreement is unlikely. When

α < 0.01, the disagreement between the sample and expected distributions

is highly signiﬁcant or the agreement is highly unlikely.

Example Problem 6.6

Statement: Consider a study conducted by a professor who wishes to determine

whether or not the 300 undergraduate engineering students in his department are

normal with respect to their heights. He determines this by comparing the distribution

of their heights to that expected for a normally distributed student population. His

height data are presented in Table 6.6. Are their heights normal?

Statistics 207

Bin

Heights

Observed

Expected

number k

in bin

number, O

number, E

less than X − 1.5σ

20.1

between X − 1.5σ and X −σ

27.5

between X − σ and X −0.5σ

45.0

between X − 0.5σ and X

57.5

between X and X + 0.5σ

57.5

between X + 0.5σ and X + σ

45.0

between X + σ and X + 1.5σ

27.5

above X + 1.5σ

20.1

TABLE 6.6

Observed and expected heights

Solution: For this case, ν = 8 − 3 = 5, where K = 8 was determined using Scott’s

formula (actually, K = 7.7, which is rounded up). The expected values are calcu-

lated for each bin by noting that E

= N P

where N = 300. For example, for bin 2

where −1.5σ ≤ x ≤ −σ, P

= P r(−1.5σ ≤ x ≤ −σ) = P r(z

= −1.5) − P r(z

−1) = 0.4332 − 0.3413 (using Table 6.2) = 0.0919. So, the expected number in bin 2 is

(0.0919)(300) = 27.5. The results for every bin are shown in Table 6.6.

Substitution of these results into Equation 6.36 yields χ

= 0.904. For the values of

= 0.904 and ν = 5, from Table 6.5, α ' 0.97. That is, the probability of obtaining

this χ

value or less is ∼97 %, under the assumption that the expected distribution is

correct. Thus, agreement with the assumed normal distribution is signiﬁcant.

6.7 *Pooling Samples

In some situations it may be necessary to combine the data gathered from M

replicate experiments, each comprised of N measurands. The measurands

can be pooled to form one set of M N measurands [18].

For the j-th experiment

¯x

i=1

and S

N − 1

i=1

− ¯x

)

. (6.37)

From these expressions the following expressions can be developed. The

mean of all ¯x

’s, called the pooled mean of x, {¯x}, the mean of the means,

then becomes

¯x = {¯x} =

j=1

¯x

j=1

i=1

. (6.38)

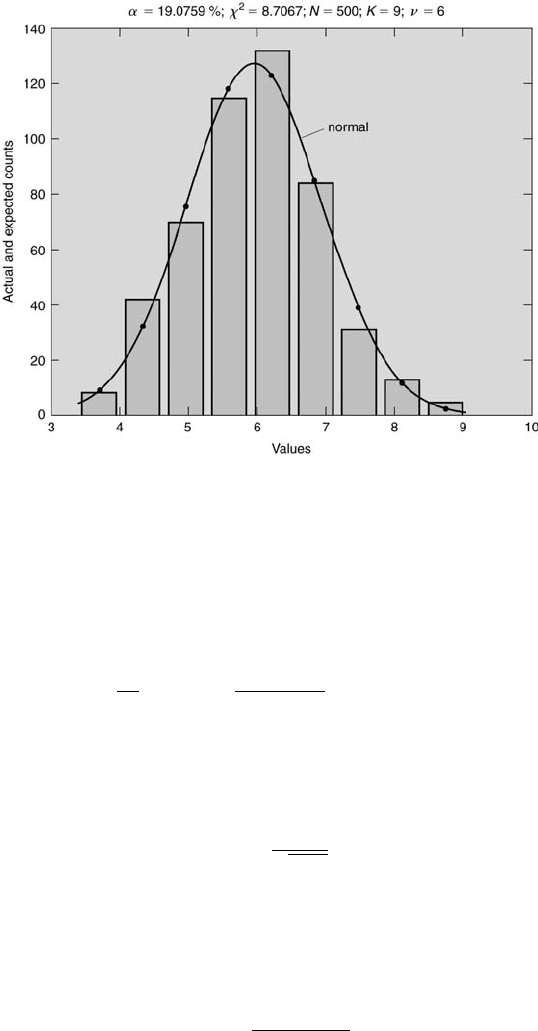
208 Measurement and Data Analysis for Engineering and Science

FIGURE 6.10

Analysis of 500 test scores using chinormchk.m.

The pooled variance of x, {S

}, is actually the average of the variances of

the M experiments where {S

} is treated as a random variable and is given

} =

j=1

M(N − 1)

j=1

i=1

− ¯x

)

. (6.39)

The pooled standard deviation, {S

}, is the positive square root of the

pooled variance. The pooled standard deviation of the means, {S

¯x

} =

}

√

. (6.40)

Now consider when the number of measurands varies in each experiment,

when N is not constant. There are N

measurands for the j-th experiment.

The resulting pooled statistical properties must be weighted by N

. The

pooled weighted mean, {¯x}

, is

{¯x}

j=1

¯x

j=1

. (6.41)

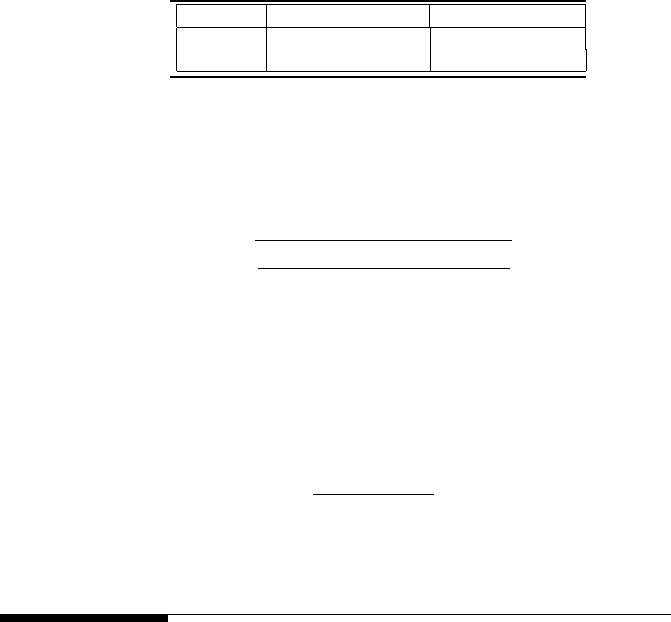
Statistics 209

accept H

reject H

true

correct (1-α)

type I error (α)

false

type II error (β)

correct (1-β)

TABLE 6.7

Null hypothesis decisions and their associated probabilities and errors.

The pooled weighted standard deviation, {S

}

, is

}

+ ν

+ ... + ν

, (6.42)

where

ν =

j=1

− 1). (6.43)

The pooled weighted standard deviation of the means, {S

¯x

}

, is

¯x

}

j=1

1/2

. (6.44)

6.8 *Hypothesis Testing

Hypothesis testing [6] incorporates the tools of statistics into a decision-

making process. In the terminology of statistics, a null hypothesis is indi-

cated by H

and an alternative hypothesis by H

. The alternative hypothesis

is considered to be the complement of the null hypothesis. There is the possi-

bility that H

could be rejected, that is, considered false, when it is actually

true. This is called a Type I error. Conversely, H

could be accepted, that

is, considered true, when it is actually false. This is termed a Type II error.

Type II errors are of particular concern in engineering. Sound engineering

decisions should be based upon the assurance that Type II error is mini-

mal. For example, if H

states that a structure will not fail when its load

is less than a particular safety-limit load, then it is important to assess the

probability that the structure can fail below the safety-limit load. This can

be quantiﬁed by the power of the test, where the power is deﬁned as 1 −

probability of Type II error. For a ﬁxed level of signiﬁcance (see Section

6.6), the power increases as the sample size increases. Large values of power

signify better precision. Null hypothesis decisions are summarized in Table

6.7.

210 Measurement and Data Analysis for Engineering and Science

Consider the rationale behind using statistical analysis to determine

whether or not the mean of a population, x

, will have a particular value,

. In an experiment, each measurand value will be subject to small, ran-

dom variations because of minor, uncontrolled variables. The null hypothesis

would be H

: x

= x

and the alternative hypothesis H

: x

6= x

. Because

the alternative hypothesis would be true if either x

< x

or x

> x

, the

appropriate hypothesis test would be a two-sided t-test. If the the null hy-

pothesis were either H

: x

≤ x

or H

: x

≥ x

, then the appropriate

hypothesis test would be a one-sided t-test. The modiﬁer t implies that

Student’s t variable is used to assess the hypothesis. These tests implicitly

require that all measurand values are provided such that their sample mean

and sample standard deviation can be determined.

Decision of either hypothesis acceptance or rejection is made using Stu-

dent’s t distribution. For a one-sided t-test, if H

: x

≤ x

, then its associ-

ated probability, Pr[X ≤ t], must be determined. X represents the value of

a single sample that is drawn randomly from a t-distribution with ν = N −1

degrees of freedom. Likewise, if H

: x

≥ x

, then its associated probability,

Pr[X ≥ t] must be found. For a two-sided t-test, the sum of the probabilities

Pr[X ≤ t] and Pr[X ≥ t] must be determined. This sum equals 2Pr[X ≥ |t|]

because of the symmetry of Student’s t distribution. These probabilities are

determined through Student’s t value. For hypothesis testing, the particular

t value, termed the t-statistic, is based upon the sample standard deviation

of the means, where t = (¯x − x

)/(S

√

N).

A p-value, sometimes referred to as the observed level of signiﬁcance, is

deﬁned for the null hypothesis of a set of measurands as the probability of

obtaining the measurand set or a set having less agreement with the hypoth-

esis. The p-value is proportional to the plausibility of the null hypothesis.

The criteria for accepting or rejecting the null hypothesis are the following:

• p < 0.01 indicates non-credible H

, so reject H

and accept H

• 0.01 ≤ p ≤ 0.10 is inconclusive, so acquire more data.

• p > 0.10 indicates plausible H

, so accept H

and reject H

Sometimes, p = 0.05 is used as a decision value in order to avoid an in-

conclusive result, where p < 0.05 implies plausibility and p > 0.05 signiﬁes

non-credibility. Keep in mind that only the plausibility, not the exact truth,

of a null hypothesis can be ascertained. Rejecting the null hypothesis of a

two-sided test means x

6= x

. Accepting the null hypothesis implies that x

is a plausible value of x

, but not necessarily that x

= x

. So, rejecting a

null hypothesis is more exact statistically than accepting a null hypothesis.

Rejecting the null hypothesis H

: x

≤ x

means x

≥ x

. Accepting the

null hypothesis indicates that, plausibly, x

≤ x

. Again, it is more exact

statistically to reject the null hypothesis or, conversely, to accept the alter-

native hypothesis. Hence, it is better to pose the null hypothesis such that

its alternative hypothesis most likely will be accepted.

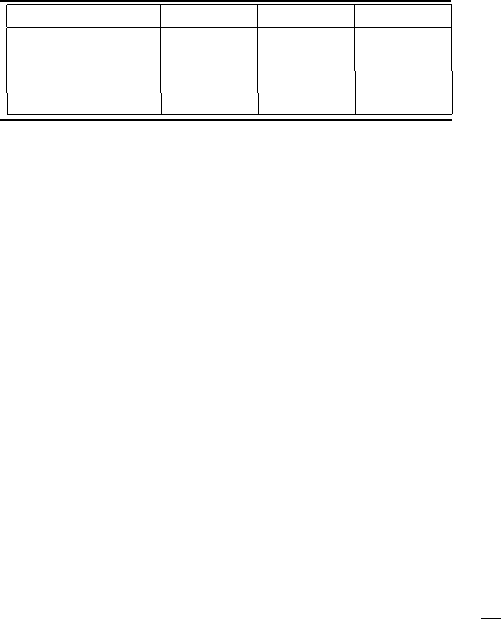
Statistics 211

p-value

α = 0.01

α = 0.05

α = 0.10

p ≥ 0.10

0.05 < p < 0.10

reject

0.01 < p < 0.05

reject

p < 0.01

reject

TABLE 6.8

Null hypothesis decisions and associated p and α values.

Stated diﬀerently, if x

is on the side of x

that favors the null hypothesis,

then the hypothesis should be accepted. If it is not, then the plausibility of

the hypothesis must be ascertained, based upon the aforementioned p-value

criteria. If the hypothesis test is one-sided, then x

≤ x

means t ≤ 0 and

p > 0.50, which indicates acceptance. Also, x

>> x

means t > 0 and

p ∼ 0, which implies rejection. Further, x

slightly greater than x

means t

is slightly greater than 0 and p is non-zero and ﬁnite, signifying plausibility.

If the hypothesis test is two-sided, the larger the value of |t|, the farther

away x

is from x

. The p-value is calculated with the probability that a

measurand set with x

= x

has a t-statistic with an absolute value greater

than |t|. Any measurand set with a t-statistic that is greater than |t| or

less than -|t| has less agreement with the null hypothesis. The acceptance or

rejection of the null hypothesis is based upon the the same aforementioned p-

value criteria. The following serves to illustrate how the p-values speciﬁcally

are determined for one-sided and two-sided hypothesis tests.

Consider the one-sided test where H

: x

≤ 10. For this example, ¯x =

12, S

= 3 and N = 20. Thus, the t-statistic value equals (12 − 10)/(3

√

20)

= 2.981. For ν = 19, the corresponding p-value equals 1 − Pr[t ≤ 2.981] = 1

− 0.9962 = 0.0038. Thus, the null hypothesis is rejected and the alternative

hypothesis, that x

is greater than 10, is accepted.

Next examine the two-sided test where H

: x

= 10. Using the same

statistical parameters as in the previous example, where the t-statistic value

is 2.981, the p-value equals 2Pr[t ≥ |2.981|] = (2)(0.0038) = 0.0076. Here the

absolute value of the t-statistic, 2.981, is greater than the p-value, 0.0076. So,

the measurand set with x

= 10 has less agreement with the null hypothesis.

In fact, because p < 0.01, the null hypothesis is not credible.

More speciﬁcity about accepting or rejecting a null hypothesis can be

obtained by associating this decision with a level of signiﬁcance, α. Here,

the null hypothesis is accepted if the p-value is larger than α and rejected

if the p-value is less than α. The level of signiﬁcance is the probability of

a Type I error. The relationships between null hypothesis acceptance or

rejection and their associated p and α values are presented in Table 6.8.

212 Measurement and Data Analysis for Engineering and Science

Set A

Set B

Test no.

(mm)

− δ

(mm)

3.0806

2.9820

0.0986

3.0232

2.9902

0.0330

2.9010

3.0728

-0.1718

3.1340

2.9107

0.2233

3.0290

2.9775

0.0514

3.1479

2.9348

0.2131

3.1138

2.9881

0.1257

2.9316

3.2303

-0.2987

2.8708

2.9090

-0.0382

2.9927

2.7979

0.1948

TABLE 6.9

Boundary-layer thickness measurements.

Example Problem 6.7

Statement: A test is conducted to assess the reliability of a transducer designed

to indicate when the pressure in a vessel is 120 psi. The vessel pressure is recorded

each time the sensor gives an indication. The test is repeated 20 times, resulting in a

mean pressure at detection of 121 psi with a standard deviation of 3 psi. Determine

the reliability of the transducer based upon a 5 % level of signiﬁcance.

Solution: It is best statistically to test the null hypothesis that the transducer’s

detection level is 120 psi. The alternative hypothesis would be that the detection level

is either less than or greater than 120 psi. This appropriate test is a two-sided t-test.

For this case, the value of the t-statistic is

t =

¯x − x

√

121 − 120

√

= 1.491.

For ν = 19, the corresponding p-value equals 2P [|t| ≥ 1.491] = (2)(0.0762) = 0.1524.

According to Table 6.8, the null hypothesis is acceptable. Thus, the transducer can

be considered reliable. At this level of signiﬁcance, the p-value would have to be less

than 0.05 before the null hypothesis could be rejected and the transducer considered

unreliable.

This type of analysis also can be employed to test the hypothesis that

two measurand sets with paired samples (each having the same number of

samples) come from the same population. This is illustrated by the following

problem.

Example Problem 6.8

Statement: Ten thermal boundary-layer thickness measurements were made at a

speciﬁc location along the length of a heat-exchanger plate. Ten other thickness mea-

surements were made after the surface of the heat-exchanger plate was modiﬁed to

improve its heat transfer. The results are shown in Table 6.9. Determine the percent

Statistics 213

conﬁdence that the plate surface modiﬁcation has no eﬀect on the thermal boundary-

layer thickness.

Solution: Assume that the thicknesses follow a t-distribution. This implies that the

diﬀerences of the thicknesses for each set, δ

A−B

= δ

−δ

, also follow a t-distribution.

The mean and the standard deviation of the diﬀerences can be computed from the

sample data. They are 0.043 mm and 0.171 mm, respectively. Now if both samples come

from the same population (here, this would imply that the surface modiﬁcation had

no detectable eﬀect on the boundary-layer thickness), then the diﬀerence of their true

mean values must be zero. Thus, the problem can be rephrased as follows. What is the

conﬁdence that a parameter with a mean value of 0.043 mm,

δ, and a standard deviation

of 0.171 mm, S

, determined from 10 samples, actually comes from a population whose

mean value is zero?

This involves a two-sided hypothesis test. The null hypothesis is that the mean

value of the diﬀerences is zero (that the surface modiﬁcation has no detectable eﬀect)

and the alternative hypothesis is that the mean value of the diﬀerences is not zero (that

the surface modiﬁcation has a detectable eﬀect). The t-statistic value for this case is

t =

√

δ − 0)

√

10(0.043)

0.171

= 0.795.

For ν = 9, the p-value equals 2P [t ≥ |0.795|] = (2)(0.2235) = 0.4470. Thus, there is

approximately a 45 % chance that the surface modiﬁcation has a detectable eﬀect and

a 55 % chance that it does not. So the present experiment gives an ambiguous result.

If the mean of the thickness diﬀerence was smaller, say 0.020 mm, given everything

else the same, then the p-value would be 0.7200, based upon t = 0.37. Now there

is more conﬁdence in the hypothesis that the surface modiﬁcation has no detectable

eﬀect. However, this still is not signiﬁcant enough. In fact, to have 95 % conﬁdence

in the hypothesis, the mean of the thickness diﬀerence would have to be 0.004 mm,

given everything else is the same. This type of analysis can be extended further to

experiments involving unpaired samples with or without equal variances [6].

6.9 *Design of Experiments

Statistical tools can be used in experimental planning. The method of de-

sign of experiments (DOE) provides an assessment of an experiment’s

output sensitivity to its independent variables. In DOE terminology, this

method assesses the sensitivity of the result (the measurand or dependent

variable) to various factors (independent variables) that comprise the pro-

cess (experiment). The signiﬁcance of DOE is that it can be carried out

before an experiment is conducted. DOE, for example, can be used to iden-

tify the variables that most signiﬁcantly aﬀect the output. In essence, DOE

provides an eﬃcient way to plan and conduct experiments.

Methods of DOE have been known for many years. According to Hald

[14], fundamental work on DOE was carried out by R. A. Fisher and pub-

lished in 1935 [8]. DOE, and the related topic, Taguchi methods, have be-

come popular in recent years because of the quest through experimentation

for improved quality in consumer and industrial products (for example, see

214 Measurement and Data Analysis for Engineering and Science

low

high

A(mm)

B(ms)

TABLE 6.10

Factors and their levels for the detector experiment.

[10], [11], and [12]). These methods also can be applied to forensic science

[13].

The main objective of DOE is to determine how the factors inﬂuence

the result of a process. The approach is to determine this by running tri-

als (actual and/or computer trials), and measuring the process response

for planned, controlled changes in the factors. A feature of DOE is that it

provides a ranking of the sensitivity of the result to each factor; it ranks

the factors in terms of their eﬀects. It provides the direction of the sensi-

tivity, whether a factor change increases or decreases the result. A major

and important feature of DOE is that it provides this information with a

minimum number of measurements or calculations. An additional advantage

of DOE is that knowledge of the statistical nature of the input is unnec-

essary. If statistical information is available, DOE can lead directly to an

analysis of variance (ANOVA) (for example, see [14]) and hypothesis tests

for the factors and their interactions. If the statistical nature of some or all

of the factors is unavailable, methods still exist to examine and rank the

sensitivity.

The basics of DOE can be illustrated readily. Consider a hypothetical

experiment with a result, y

, that depends on a number of factors desig-

nated by A, B, C, .... Trials of the experiment are conducted for diﬀerent,

predetermined values of the factors, where the j -th run produces the j -th

value of the result. The primary function of DOE is to determine a quanti-

tative measure of the eﬀect of each of the factor changes on the result. The

output must be quantitative or measurable. The factors can be quantitative.

They also can be attribute variables, such as hot or cold, fast or slow, and

so forth. In the coverage here, factors will be allowed to take on only two

values called a low level, indicated with a minus sign, and a high level, in-

dicated with a plus sign. The high and low levels of the factors are selected

by the experimenter to represent a practical range of values large enough to

have an inﬂuence, yet small enough to determine the local behavior of the

process. It is not uncommon to carry out one exploratory DOE to establish

ranges of variables, and then perform another DOE, based on the results

of the ﬁrst, for a more reﬁned analysis. In the case of attribute variables,

such as fast and slow, the choice of high and low can be purely arbitrary.

In the case of quantitative variables, the choice usually is intuitive, but it

still remains arbitrary because the signs of the results reverse if the levels

are reversed.

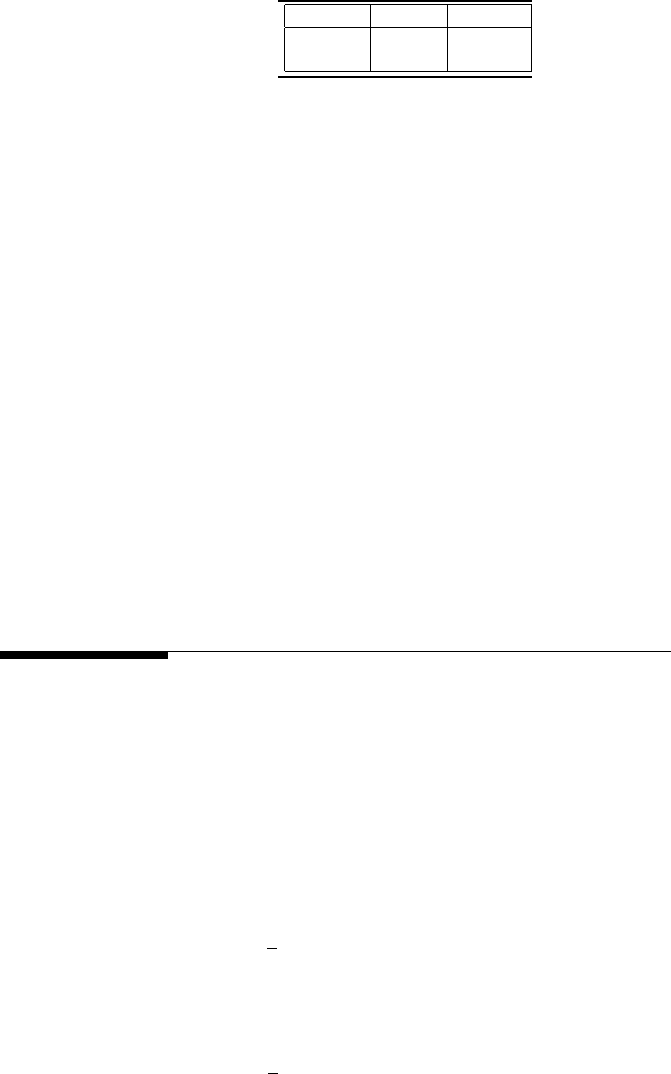
Statistics 215

A: low

A: high

B: low

40.9

47.8

B: high

42.4

50.2

TABLE 6.11

Percentage changes for four trials.

To illustrate the method of DOE, consider a hypothetical experiment

in which an experimentalist wishes to assess the sensitivity of a light-level

detector to two factors, the position of the detector from the surface of

an object (factor A) and the time response of the detector (factor B). The

percentage change in the amplitude of the detector’s output from a reference

amplitude is chosen as the result. Table 6.10 lists the factors and their levels.

Four trials are carried out. This provides a complete experiment, in which

all four possible combinations of factor type and level are considered. In one

trial, for example, the detector with the shortest time response, 20 ms (the

low value of B), is placed near the surface, at 5 mm (the low value of A). The

result for this case is an increase in the amplitude of 40.9 %, as displayed

in Table 6.11. Examination of all of the results reveals that the greatest

output is achieved by placing a 50-ms detector 10 mm from the surface of

the object. DOE can be extended readily to consider more than two factors.

To achieve a complete experiment, 2

trials are required, where k is the

number of factors, with two levels for each factor.

6.10 *Factorial Design

The method of DOE suggests a manner in which the contribution of each

factor on an experimental result can be assessed. This is the method of

factorial design. Because this method identiﬁes the eﬀect of each factor,

it can be used to organize and minimize the number of experimental trials.

When dealing with the eﬀects of changes in two factors, two levels and

four runs, a measure of the eﬀect, or main eﬀect, ME, resulting from chang-

ing a factor from its low to high value can be estimated using the average

of the two observed changes in the response. So for factor A,

[(y

− y

) + (y

− y

)] . (6.45)

Similarly, a measure of the eﬀect of changing factor B from its low to high

level can be estimated by averaging two corresponding changes as

[(y

− y

) + (y

− y

)] . (6.46)